航空长航时惯导系统定位精度评估方法研究
(中国飞行试验研究院,西安 710089)
自20世纪80年代起,我国开始自主研制航空惯导系统。军民用飞机加装惯导系统后,可有效提高导航精度和导航余度。随着惯性技术的迅速发展,航空惯导系统的定位精度也越来越高。为此,寻求和探索评估定位精度的技术成为航空惯导系统飞行试验研究的重要关注点[1-2]。本文在分析了惯导系统工作原理的基础上,对定位精度评估的两种方法进行了深入研究和比较。通过飞行试验手段,将惯导系统和全球定位系统(GPS)加装于同一架飞机上,同步测试记录它们的输出数据。以差分GPS数据作为基准,用两种方法计算惯导系统的定位误差,通过对多架次的飞行试验数据计算结果的比较,研究分析两种评估方法的应用范围,以探知航空惯导系统定位精度的科学评估方法,为航空惯导系统的工程应用和研究积累资料和经验。
1 惯导系统定位精度评估方法
1.1 惯导系统定位误差的一般表达式
由惯导系统的工作原理可知,惯导系统的误差源包括:加速度计的零位偏差;陀螺漂移率;陀螺、加速度计的标度因子误差;陀螺、加速度计的安装误差;平台的初始姿态和初始位置误差以及基准测量设备本身的误差等。其中,未经补偿的陀螺漂移率是决定定位误差的主要因素。这是因为陀螺漂移率所引起的定位误差是随时间积累的,而其他各误差源引起的定位误差都是有界的[3-4]。鉴于此,针对不同的导航时间,应采用不同的定位精度评估方法。
相关文献资料指出,惯导系统的各种误差源综合作用的定位误差是遵循正态分布的。
设在t时刻飞机的真实位置在M0处,而惯导测得的飞机位置在Mi处,则为飞机的位置误差。它在东向和北向的分量为rx和ry,即:。
若由惯导系统测得的飞机位置以概率50%落入以M0为中心,某一长度R为半径的圆内,则称R为50%圆概率误差(CEP)(图1)。
用x、y分别表示惯导系统的位置误差分量rx、ry,则为一个二维随机变量。由于惯导系统的定位误差分布服从一维正态分布,惯导南北距离误差(纬度误差)和东西距离误差(经度误差)的分布密度函数也是正态的,惯导定位的经度误差和纬度误差相互独立且分别遵从不同参数的正态分布,故(x,y)的联合分布密度函数形式为:

图1 圆概率误差定义Fig.1 Definition of CEP

式中,x、y分别表示经度误差和纬度误差,μx、σx、μy、σy分别表示相应的数学期望和均方根误差。
对式(1)积分,并令其等于50%,得:

式中,R即为惯导位置误差的圆概率误差。
1.2 导航时间较短时圆概率误差的拟合
根据经验得知,在导航时间较短时(一般为1h内),惯导系统的径向位置误差可近似看成呈直线式发散,因此可将其拟合成一条直线,用最小二乘法来确定该直线的系数,令该直线方程为:

式中,j为采样点;tj为系统从零时刻到第j个采样时刻所经过的导航时间;Rj为tj时刻的径向位置误差;A为系数。
由于t时刻径向位置误差的真值可表示为如下形式:

式中,为第j个采样时刻的纬度误差,(′);为第j个采样时刻的经度误差,(′);φj为第j个采样时刻的纬度真值,(°)。
故此拟合直线的残差:

其残差平方和为:

式中,m为采样点数。
为求残差平方和S的最小值,有,即:

化简得:

式中,A即为导航定位误差的径向误差率,由此计算得出的径向误差率可以较真实反映出惯导位置误差随导航时间的变化率,单架次的定位误差可以用径向误差率的均方根来衡量。
设有n次试验,则n次试验的圆概率误差为:

式中,K可根据选定的概率查表求得[3],由此得到的CEP值是值得信赖且被用户认可的。
1.3 导航时间较长时圆概率误差的拟合
惯导系统的各种误差源综合作用的定位误差遵循正态分布,但其亦随导航时间的积累而发散。长时间导航情况下,整个导航过程中定位误差不可能有一个统一的数学期望和方差,故不能把全过程做一次性统计平均;另外,惯导定位误差是多种振荡相互调制的,直接采用回归直线拟合也是不恰当的。
式(2)给出了圆概率半径的精确定义式,亦可写成如下形式:

通过非中心χ2分布拟合和中心χ2分布的常数倍拟合,得到了50%圆概率误差的近似表达式和圆概率误差的近似表达式。

其中,Zp'可根据选定的概率查表求得[5];;。长航时惯导系统的定位精度由评定时间间隔内所有采样时刻圆概率半径RP的最大值来衡量。
2 飞行试验
2.1 试验条件
选用某型飞机作为试验载体,在飞机上加装惯导系统和测试基准设备(差分GPS),惯导系统输出数据由加装的机载数据采集记录系统记录。
2.2 试验方法
针对不同航线飞行过程中惯导系统定位误差特性的不同,设计了东-西航线和南-北航线各4架次的试飞,飞行状态以本试验机的巡航高度和巡航速度为主。试飞中同步采集测试记录系统的时标信息、GPS输出信息和惯导系统的输出信息(每2s取一个采样点)。
飞行后,按照拉依达法则对每架次的惯导数据进行奇异值剔除,按照两种圆概率误差的计算方法,分别对惯导系统的定位误差进行计算。
3 试验结果分析及结论
3.1 试验结果分析
试飞8架次导航10h的径向位置误差曲线如图2所示,从图2中8个架次的径向位置误差曲线可以看出,导航10h内径向位置误差的整体变化趋势发散,即径向位置误差随导航时间的增加而呈现以舒拉振荡为周期的递增现象。
按照方法一计算导航n(1≤n≤10)小时内定位误差(圆概率误差CEP),统计结果见表1。
(1)由图2可以看出,径向位置误差的绝对值随导航时间的增加而变大;
(2)由表1可知,位置误差(圆概率误差CEP)随导航时间的增加而减小。
通过对试飞数据的分析,发现经过长航时导航后,方法一计算得出的CEP值已经不能真实反映出定位误差随导航时间的变化情况。
但是,由图2看到,随着导航时间的增加,在导航10h内,惯导系统的径向位置误差曲线呈现明显的舒拉周期式振荡递增。原因在于:惯导位置误差由趋势项和振荡项两部分组成,当导航时间经历多个舒拉周期时,系统位置误差中的舒拉振荡和地球振荡相互调制效果明显,且振荡项与趋势项叠加,造成径向位置误差呈振荡型发散[3]。因此,采用方法一的径向误差率来评价长航时导航定位误差已不再适用。对于长航时惯导系统而言,考虑采用方法二对定位误差进行评估。
采用方法二对惯导系统导航10h的定位误差进行统计计算,其定位误差的圆概率半径曲线如图3所示,该曲线呈舒拉周期式振荡递增的趋势,与径向位置误差的变化趋势是相同的,且其最大值为1.176n mile,即该惯导系统的导航定位精度为1.176n mile/10h。
采样方法二计算得到的各采样时间CEP如表2所示。结果表明,方法二计算得到的定位精度更贴近实际结果,能够真实反映位置误差随时间的变化趋势。

图2 单架次径向位置误差曲线Fig.2 Curve of radial position error in signal sortie

表1 位置误差的圆概率误差(方法一)
3.2 试验结论
通过对长航时惯导系统试飞数据的分析,得出以下结论:
(1)对于导航时间较短(1h内)的情况,惯导系统的定位精度可以通过计算位置径向误差率的圆概率半径来衡量;
(2)对于导航时间较长的情况,方法一不再适用于计算其定位精度,采用方法二计算评定时间间隔内所有采样时刻圆概率半径的最大值来衡量其定位精度是可行的。
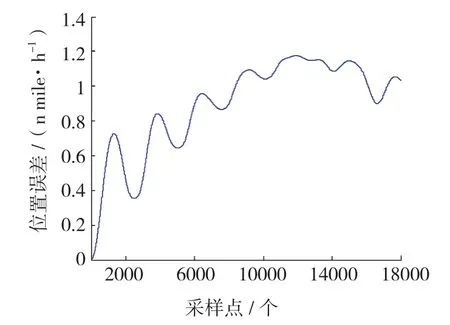
图3 定位误差统计结果曲线(方法二)Fig.3 Curve of statistical result of position error (method 2)

表2 位置误差的圆概率误差(方法二)
4 结束语
航空惯导系统是军民用飞机上重要的导航信息源,对其定位精度进行科学的评估尤为重要。根据导航时间的长短来选择合适的评估方法,是较为科学的手段,得到的评估结果可被用户和研制方接受。
[1]MAREK D,CEZARY S.Position accuracy evaluation of the modernized polish DGPS[J].Polish Maritime Research,2009,16(4):56-60.
[2]ZHANG X,CANNON M E.Integration of GPS with a medium accuracy INS for meter-level positioning using a wave estimator[C]//ION 58th Annual Meeting and CIGTF 21st Guidance Test Symposium.Albuquerque,USA,2002:9.
[3]何钟麟.舰船惯性导航系统定位精度评定及其圆概率半径[J].船舶工程,1984(3):5-6.
HE Zhonglin.Evaluation of position accuracy and its radius of the circle of equal probability of ship inertial navigation system[J].Ship Engineering, 1984(3):5-6.
[4]秦永元.惯性导航[M].北京:科学出版社,2006:255-257.
QIN Yongyuan.Inertial navigation[M].Beijing:Science Press, 2006:255-257.
[5]罗勤振,韩福江.GJB 729-1989 惯性导航系统精度评定方法[S].北京:中国船舶工业总公司,1989.
LUO Qinzhen, HAN Fujiang.GJB 729-1989 Evaluation method of position accuracy of inertial navigation system[S].Beijing:CSSC,1989.

