基于加工能力模糊聚类的设备分组方法

周媛媛 ，田锡天 ，黄利江 ，辛宇鹏 ，马光辉

（1.西北工业大学CAPP与制造工程软件研究所，西安 710072；2.中航工业西安航空发动机（集团）有限公司，西安 710021）

工艺设计是连接产品设计和制造的桥梁，是生产制造的前提。加工设备的确定是工艺设计的重要步骤之一。工艺人员往往是依据经验确定加工设备，因此加工设备的选择结果受工艺人员经验水平的影响很大，不利于资源的合理利用。面向工艺设计，根据设备的能力对设备进行合理分组，可以根据工艺要求在设备组中快速选择符合要求的加工设备，提高设备选择的准确性、高效性，实现资源优化配置，同时也减少人员参与，为工艺设计中的自动化决策提供条件。

目前设备的分组方法主要概括为两种：一种是按照设备的类别进行分组的方法，如机械设备可分为金切机床、锻压设备和铸造设备等，金切机床又可分为车床、铣床、刨床、钻床等，以此类推继续细化分类。这样的设备分组方法，虽然有利于设备的管理，但是对于工艺设计来说，同一加工特征可以用不同类别的设备进行加工，同一设备也可以加工不同的加工特征，因此按类别对设备分组的方法不利于工艺设计过程中对设备的选择。另一种方法是将设备构建成制造单元，满足某类零件的加工。近几十年来，很多学者对制造单元的构建技术做了大量研究：考虑加工时间、加工顺序、生产批量等生产约束条件，建立了分别以加工成本最少、运输成本最少、物流总量最小、最佳设备及单元平衡等为目标的数学模型[1]，通过聚类分析法、遗传算法、神经网络、粒子群优化算法等方法实现制造单元的构建[2-5]。但大多数研究都是在已知零件可选设备的基础上，对这些可选设备进行组合，构成完成某种加工任务的制造单元。而很少从零件加工设备的选择角度研究如何将设备进行分组。石旭东等[6]根据设备具有的工艺元素，应用扩展模糊C-均值聚类算法（EFCM）对设备进行分组，形成加工单元。这种分组方法使每个设备只能属于一个加工单元，但有些设备的工艺元素却无法全部包含在一个加工单元中。

本文采用加工能力元来描述设备的加工能力，形成设备与加工能力元的对应关系，应用区间数模糊C-均值（FCM，Fuzzy C-means）聚类算法对加工能力元进行聚类分组，进而对设备进行分组。每个设备根据所拥有的多种加工能力可以被分到不同的组中。

1 基于加工能力模糊聚类的设备分组方法

在机加工艺设计中，工艺人员根据加工能力选择满足工艺要求的加工设备。本文采用加工能力元对设备的加工能力进行描述。加工能力元（MCE，Machining Capability Element）是以加工特征为核心的加工能力信息所形成的实体，可以表示为：mce=（A1，A2，…，AN），其中，A1是与零件加工特征有关的能力参数，如加工零件的种类、加工特征的类型、可加工零件的尺寸、可达到的精度（包括尺寸精度、形状精度、位置精度、表面质量）、生产批量等。图1描述了加工能力元与设备的关系，可以看出每个设备的加工能力可以用多个加工能力元描述，同时每个加工能力元表达的加工能力也可以选择不同的设备进行实现。因此，根据加工能力对设备进行分组，在工艺设计中可以依照零件的加工特征匹配相应的加工能力元，进而找到可选设备组，再根据具体情况从可选设备组中确定具体的设备对零件进行加工。

设备分组过程如图2所示，首先根据设备的加工能力提取相应的加工能力元，并生成加工能力元与设备的对应关系数据。然后将加工能力元根据可加工特征类型、可加工零件类别2个参数进行粗略分类。可加工特征类型可分为平面、外圆柱面、孔、螺纹、键槽、齿面等；可加工零件类别可分为轴套类、轮盘类、叉架类、箱体类等。在对加工能力元分类的基础上，根据加工能力元其余参数（如可加工零件的长度、可达到的精度范围、可达到的表面粗糙度、生产批量等）对加工能力元进行模糊聚类分组。最后，在加工能力元模糊聚类的基础上，根据加工能力元与设备的对应关系对设备进行分组。

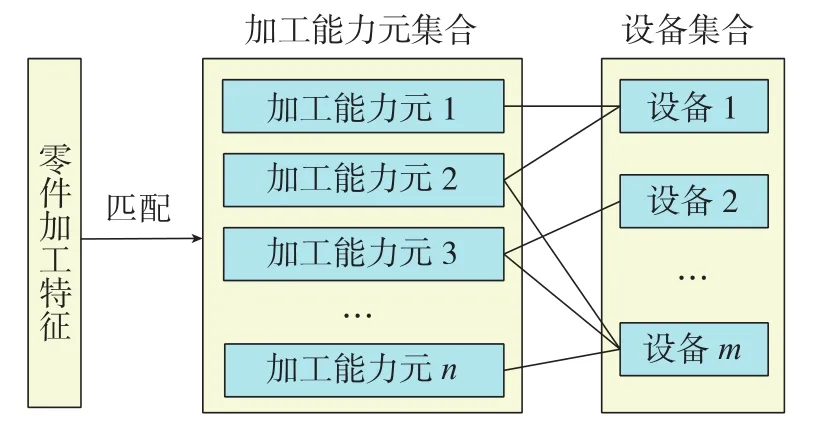
图1 加工能力元与设备的关系Fig.1 Relationship between machining capability elements and machines

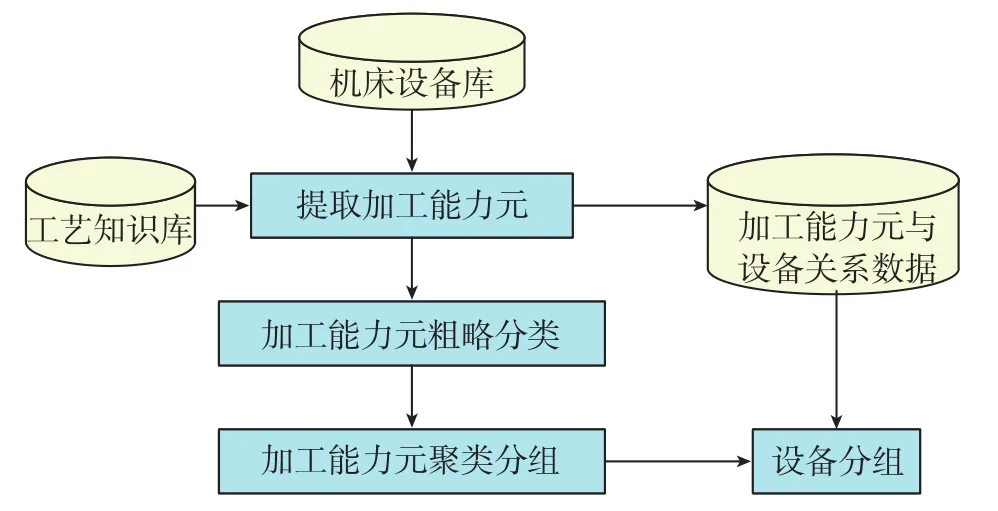
图2 设备分组过程Fig.2 Machine grouping process

2 加工能力元的模糊聚类模型

FCM聚类算法是一种应用较为广泛的基于划分的聚类方法，该算法用模糊隶属度来表示对象属于某个类的程度，通过解的多次迭代得到目标函数的优化解。由于加工能力元参数的取值一般为区间数值型，传统的FCM聚类算法无法满足聚类要求，因此本文采用一种区间数FCM聚类算法对加工能力元进行分组。

设有n个加工能力元MCE={mce1，…，mcen}，每个加工能力元表示为，j=1，2，…，n，N为加工能力元参数的个数。

已知：（1）n个加工能力元参数A1（加工零件的类别）的值相同，同时参数A2（加工特征的类型）的值也相同的，即；（2）参数A3，A4，…，AN的值为区间数值的形式，表示为k=3，4，…，N；j=1，2，…，n，其中。

将n个加工能力元分成c组，分组中心为V=（v1，v2，…，vc），其中，k=3，4，…，N，i=1，2，…，c。uij为每个加工能力元 mcej对各分组中心vi的隶属度。建立目标函数如下：

式中，d（vi，mcej）为加工能力元与分组中心之间的距离，即mcej和vi间的相似性度量，距离越小，相似度越高。本文引入区间数的距离公式[7]来度量加工能力元与分组中心之间的距离。

设区间数，其中，，则a与b间的距离定义为：

（1）当a=b时，d（a，b）=0 ；

（2）当a≠b时，

加工能力元与分组中心vi=间的距离可以表示为：

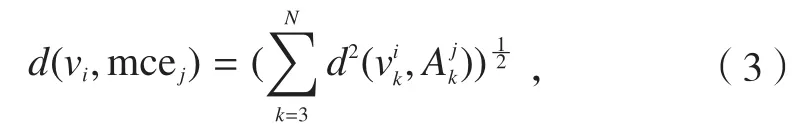
同理，任意两个加工能力元和，j1,j2∈ {1,2,···,n} 间的距离可以表示为：

式（1）的迭代解为：

经多次迭代求得每个加工能力元mcej对各分组中心vi的隶属度uij后，根据最大隶属度原则，mcej对哪个分组中心的隶属度最大，就将其归入那个分组中，即若µi0j=max{µij|i=1,2,···,c}，i0={1，2，…，c}，则将 mcej分到第i0组。

3 加工能力元模糊聚类分组过程

3.1 初始分组中心选择

FCM聚类算法是一种局部搜索算法，为防止计算结果收敛于局部最优解，需要合理选择初始分组中心。本文采用文献[8]中的一种改进的最大最小距离算法，进行初始分组中心的选择。初始分组中心选择步骤如下。

步骤1：确定分组数c，2≤c≤n，其中n为加工能力元的个数。

步骤2：计算任意两个加工能力元间的距离d(mcej1,mcej2)，j1，j2=1，2，…，n。找出距离最大的两个加工能力元和，即，作为第一和第二聚类中心；令r=2。

步骤3：如果c=2，则跳至步骤5；否则，计算除聚类中心外的任意加工能力元mcej与聚类中心的距离d(mcej,mceph)，j=1，…，n且mcej∉ {mcep1,···,mcepr}，h=1，…，r。 若且，则即为第r+1聚类中心；更新r=r+1。

步骤4：如果r=c，则跳至步骤5；否则跳至步骤3。

步骤5：将各加工能力元按最小距离原则分到各组中，即若n，则加工能力元mcej分到mcep所在的组中，此时得到一个粗分组。

步骤6：计算各粗分组的中心。

式 中，i=1，2，…，c;k=3，4，…，N ；j=1，2，…，n；Ni为第i组中加工能力元的个数；Gi表示第i组。V0=(v01,v02,···,v0c)即为初始分组中心。

3.2 加工能力元模糊聚类分组算法

加工能力元的模糊聚类分组算法如下。

步骤1：根据式（8）对数据进行规范化处理，

式中，。例如，对参数A4（mm）的值[200，600]、[750，1000]、[1500，2000]进行规范化处理，则（A4）max=2000， （A4）min=200，（A4）max-（A4）max=2000-200=1800。按公式（8）计算，规范化结果分别为 [0，0.2222]、[0.3056，0.4444]、[0.7222，1]。

步骤2：确定分组数c，给定一个小正数ε（如10-2，10-3，10-4，…），设置迭代计数b=0（分组数c可参照文献[9]进行确定）。

步骤3：用3.1节介绍的改进的最大最小距离算法选择初始分组中心vi(0)(i=1,2,···,c)。

步骤4：根据公式（5）计算每个加工能力元对各分组中心的隶属度µij(b)(i=1,2,···,c;j=1,2,···,n)。

步骤5：根据公式（6）更新各分组中心vi(b+1)(i=1,2,···,c) 。

步骤6：若，则停止迭代，；否则令b=b+1，转向步骤4。

步骤7：按照最大隶属度原则，对加工能力元进行分组。

4 实例验证

本文从某企业叶片加工车间选择15台加工设备，以此为例说明该分组方法的过程及实用效果。15台设备对叶片类零件的叶身型面进行加工的能力描述如表1所示。

首先根据这15台设备的加工能力，总结出加工零件的类别为叶片，加工特征的类型为叶身型面的加工能力元共10个。加工能力元的参数为：加工零件的类别（A1）、加工特征的类型（A2）、特征的长度范围 （A3/mm）、轮廓度（A4/mm）、位置度（A5/mm）、表面粗糙度Ra（A6/μm）及适应的生产批量（A7/件）。表2列出各加工能力元参数信息及对应加工设备。

应用模糊聚类算法对加工能力元分组。设分组数c=4，小正数ε=10-5。表3为经计算所得初始分组中心，再经6次迭代运算得最终分组中心，如表4所示。表5列出加工能力元对最终分组中心的隶属度。

根据最大隶属度原则，由表5可得到加工能力元的分组结果。由表2可得加工能力元与设备的对应关系。加工能力元及相应设备的分组结果如表6所示。

（1）对单独一个参数来说，分组结果并没有将参数值相近的加工能力元全部分到同一组中。例如，对于参数A5（位置度），mce4与mce6具有相同的值，但并没有被划分到同一组中。

表1 设备加工能力描述

表2 加工能力元参数及对应设备信息

表3 初始分组中心各参数值

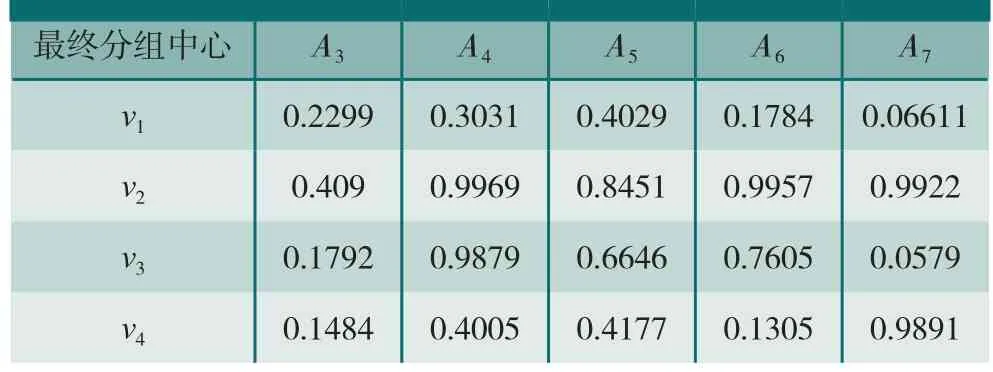
表4 最终分组中心各参数值

表5 加工能力元对各分组中心隶属度

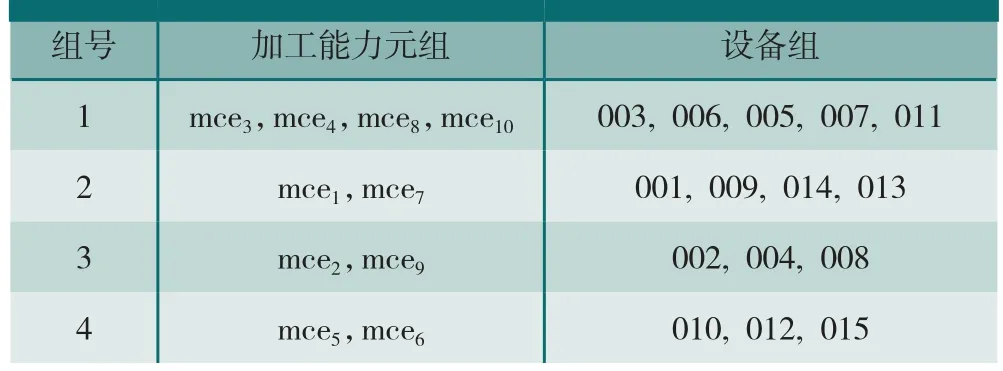
表6 加工能力元及设备分组结果

（2）综合这5个参数，可以看出分到同一组的加工能力元各参数的值非常相近，具有很高的相似度；而分到不同组的加工能力元各参数的值相差很大，相似度很低。

（3）试验中，算法的迭代次数为6，小于10。

综上所述，基于加工能力模糊聚类的设备分组方法，将相似性高的加工能力元分到同一组中，进而将加工能力相似的设备划分到同一设备组中，满足设备分组的要求；通过选择初始分组中心，使算法的迭代次数控制在10以内，既提高了运算效率，又保证了分组结果的稳定性。

5 结束语

本文首先提出了基于加工能力模糊聚类的设备分组方法，引入加工能力元描述设备的加工能力。然后建立了加工能力元聚类分组的问题模型，详细讨论了应用区间数FCM聚类算法的加工能力元的聚类分组过程，给出了初始分组中心的选择过程。最后实例验证表明，该方法能很好地满足设备分组的需求，提高了设备的有效利用率，有利于资源的优化配置。下一步应重点研究如何制定有效的选择策略，实现对设备的合理选用。

[1]王爱民，丁国智，宁汝新.制造单元快速构建技术研究[J].北京理工大学学报，2006，26(10):85-99.

WANG Aimin，DING Guozhi，NING Ruxin.Rapid design technology for manufacturing cells[J].Transactions of Beijing Institute of Technology，2006，26(10):85-99.

[2]陈华伟，王爱民，宁汝新.制造单元构建过程中的模块化聚类分析[J].华中科技大学学报（自然科学版），2012，40(S2):87-90.

CHEN Huawei，WANG Aimin，NING Ruxin.Modularized cluster analysis during manufacturing cell formation[J].Journal of Huazhong University of Science and Technology(Natural Science Edition)，2012，40(S2):87-90.

[3]刘雪梅，朱丽君，李爱平，等.基于遗传算法的生产车间制造单元构建技术研究[J].制造技术与机床，2013(2):50-54.

LIU Xuemei，ZHU Lijun，Li Aiping，et al.Research of cell formation technology based on genetic algorithm[J].Manufacturing Technology and Machine Tool，2013(2):50-54.

[4]王国新，阎艳，宁汝新，等.模糊神经网络与启发式算法相结合的制造单元构建方法[J].计算机集成制造系统，2008，14(11):2175-2183.

WANG Guoxin，YAN Yan，NING Ruxin，et al.Manufacturing cell formation approach combing fuzzy neural network with heuristic algorithm[J].Computer Integrated Manufacturing Systems，2008，14(11):2175-2183.

[5]王雷，唐敦兵，许美健，等.基于粒子群优化算法的制造单元聚类研究[J].计算机集成制造系统，2009，15(2):328-333.

WANG Lei，TANG Dunbing，XU Meijian，et al.Clustering of manufacturing cells based on particle swarm optimization[J].Computer Integrated Manufacturing Systems，2009，15(2):328-333.

[6]石旭东，付宜利，代勇，等.基于模糊聚类的设备分组技术[J].哈尔滨工业大学学报，2001，33(3):287-290.

SHI Xudong，FU Yili，DAI Yong，et al.Machines grouping base on fuzzy clustering[J].Journal of Harbin Institute of Technology，2001，33(3):287-290.

[7]TRAN L，DUCKSTEIN L.Comparison of fuzzy numbers using a fuzzy distance measure[J].Fuzzy Sets and Systems，2002，130(3):331-341.

[8]单凯晶，肖怀铁.初始聚类中心优化选取的核C-均值聚类算法 [J].计算机仿真，2009，26(7):118-121.

SHAN Kaijing，XIAO Huaitie.A kernel C-means clustering algorithm with meliorated initial center .Computer Simulation，2009，26(7):118-121.

[9]周世兵，徐振源，唐旭清.新的K-均值算法最佳聚类数确定方法[J].计算机工程与应用，2010，46(16):27-31.

ZHOU Shibing，XU Zhenyuan，TANG Xuqing.New method for determining optimal number of clusters in K-means clustering algorithm[J].Computer Engineering and Applications，2010，46(16):27-31.