对一类磁场中带电粒子的轨迹问题的解法探讨

刘先兵

在高考中，研究磁场中带电粒子的轨迹问题一般都是已知磁场的边界，根据条件寻找所需要的粒子运动轨迹，然后利用几何关系和公式解题。其中寻找粒子的运动轨迹是解题思路中最关键的环节。但是，也有一类题型是磁场范围未知而要你确定磁场范围和边界。由于磁场范围未知，这类题目往往会给学生一种无从下手的感觉。下面我对这类题目谈谈自己的见解。

（1）b点的坐标；

（2）粒子从O点进入磁场区到达b点所经历的时间；

（3）圆形磁场区的最小面积。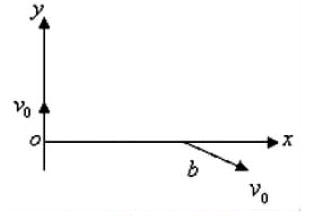

【解析】本题中由于磁场范围未知，因此确定粒子的运动轨迹是本题的关键，也是本题的难点。那么下面介绍的就是确定粒子的运动轨迹的具体方法。

【方法一】如下图，利用带电粒子在磁场中轨迹的对称性。

第一步：将O点初速度和b点的出射速度反向延长线交于a点；

第二步：作出∠Oab的角平分线于x轴交于O′点；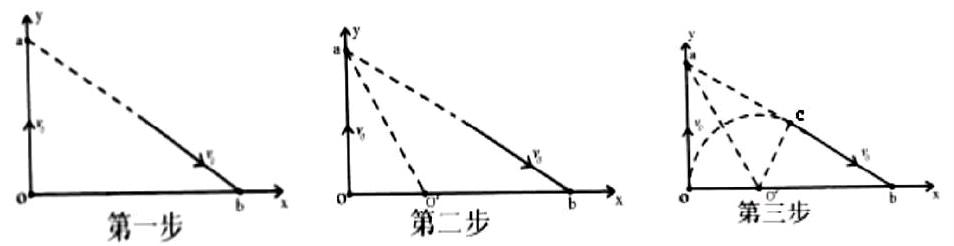

第三步：以O′为圆心，以OO′为半径作圆与ab相切于c点。圆弧Oc即粒子运动轨迹。

【方法二】如下图，抛开磁场范围未知带来的干扰，当做范围无限大，那么粒子在磁场中的轨迹一定是一个完整的圆。那么当磁场有边界的时候，无论是进入点还是出射点的速度都是沿着圆的切线，而两个切点就是磁场边界上的两点，两个切点间的圆弧就是粒子的运动轨迹。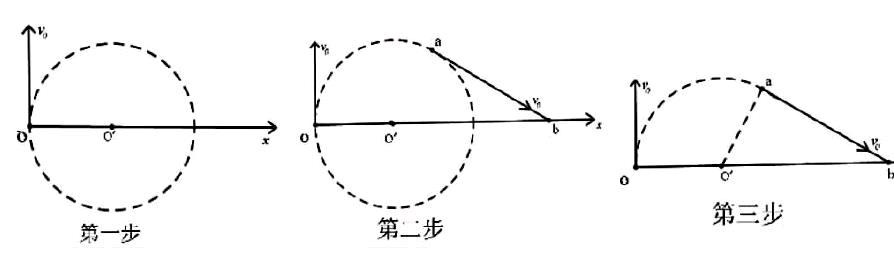

第一步：以x轴上任一点O′为圆心，以任意长度为半径作圆与x轴相切；

第二步：在圆上找出与x轴正方向成30°的切线ab，相切点为a；

第三步：去掉多余部分，连接O′a，圆弧Oa即粒子的运动轨迹。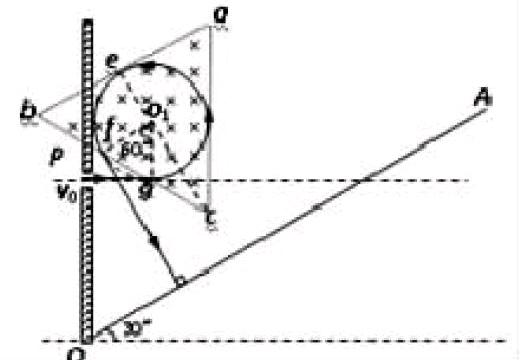

【解答】粒子的运动轨迹如下图所示：