基于Sarmanov相依分布的破产概率研究

文丽壹，郭晓莉

(重庆理工大学 数学与统计学院，重庆　400054)



基于Sarmanov相依分布的破产概率研究

文丽壹，郭晓莉

(重庆理工大学 数学与统计学院，重庆400054)

摘要：考虑带有保险风险和金融风险的离散时间风险模型，假设保险风险和金融风险都属于强正则变化族并且服从Sarmanov相依分布，得到了一些有限和无限时间的精确的破产概率渐近表达式。

关键词：Sarmanov相依；保险风险；金融风险；破产概率

保险公司的资产在随机经济环境中将会导致两种风险[1]，我们称其为保险风险和金融风险。其中：保险风险是传统保险索赔引起的责任险；金融风险是保险公司的资产在金融市场上作风险投资引起的投资风险[2]。在随机经济环境下，根据保险实务和金融市场规律，本研究作如下假设：① 保险公司每个周期i的保费收入为Ci，支出为Ai,Ci和Ai为随机变量且Ci>0,Ai>0；② 随机通胀因子或随机累积因子为Bj=1+rj；③ 保险公司的初始资本为x，保险公司在有限时间n的财富为Un。综上可得：

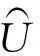
(1)

注记1如果设保险公司的风险投资比例系数为p,p∈[0,1],Wi表示投资组合的价值，于是Wi=(1-p)Wi-1(1+r)+pWi-1(1+ri),则随机通胀因子Bj=Wi/Wi-1=(1-p)(1+r)+P(1+ri),从而对应的金融风险Yj=1/[(1-p)(1+r)+p(1+ri)]。

(2)

(3)

与有限时间相对应的无限时间n→∞的破产概率可表示为

(4)

或

(5)

本文结合文献[10-11]的研究成果，研究保险风险与金融风险都属于强正则变化族并且满足Sarmanov相依分布的情形，得到了一些有限时间和无限时间的精确破产概率渐近表达式，推广了文献[11]的结果。

1准备工作

首先，考虑保险风险的分布族以及相依分布关系。

定义4[10]Sarmanov相依分布。假设随机对(X,Y)服从二元Sarmanov分布，则:

(6)

其中:θ为实常数；核函数φ(x),φ(y)满足Eφ(x)=Eφ(y)=0，且1+θφ(x)φ(y)≥0在定义范围内成立。DX={p(X∈(x-δ,x+δ))>0,x∈R}，DY={p(Y∈(x-δ,x+δ))>0,y≥0}，且DX,DY有界。显然，如果θ=0或 φ(x)=0或φ(y)=0,则X与Y是相互独立的。现在考虑的是θ≠0和核函数φ(x),φ(y)≠0的情形。 由文献[10]知φ(x),φ(y)有以下3种选择：

1) φ(x)=1-2F(x),φ(y)=1-2G(y)。此时的二元Sarmanov相依分布为标准的二元Farlie-Gumbel-Morgenstern相依分布。

2)φ(x)=(exp(-x)-c)Ⅱ{x≥0},其中c=Eexp(-X)Ⅱ{x≥0}/p(X≥0),φ(y)=exp(-y)-Eexp(-Y)。

3)φ(x)=xp-EXp，φ(y)=yp-EYp。

2主要结论及其证明

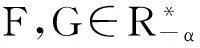
定理1设{(X,Y),(X1,Y1),…,(Xn,Yn)}是独立同分布随机对序列，且随机对(X,Y)服从二元Sarmanov分布。如果(X,Y)满足上述假设条件，则：

(7)

(8)

在证明定理之前需要介绍几个引理，这几个引理在证明过程中起着至关重要的作用。有关这些引理的证明可以参考文献[10-11]。

引理1设分布F1,…,Fn在R上，如果对每一个p∈Δ，有Fp∈S(α),α≥0，则

(9)

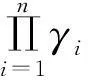
(10)

引理2是Breiman’s定理[4]的一种变形。

以下证明定理1成立。

(11)

又由核函数有界知limφ(x)=d1, limφ(y)=d2存在,因此：

于是根据引理2和式(11)可得

(12)

定义Mn的等价分布为(Xn+Mn-1)+Yn,n∈N,接着用归纳法证明定理1成立。

(13)

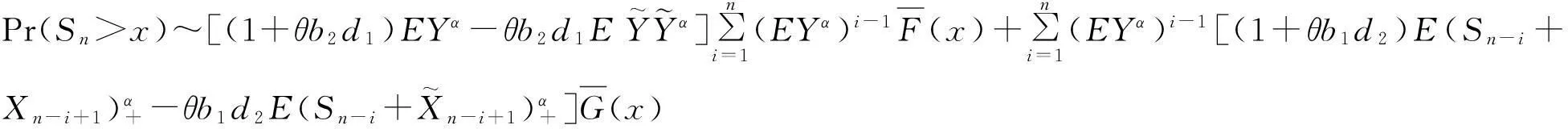
注记3若在Sarmanov分布中，核函数φ(x)=1-2F(x),φ(y)=1-2G(y),此时|φ(x)|= |φ(y)|=b1=b2=1,limφ(x)=limφ(y)=d1=d2=-1,则：

(14)

(15)

即文献[11]中对应的注记2.1(a)。

定理2在定理1成立的前提下，如果EYα<1，则n→∞，有

(16)

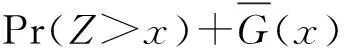
(17)

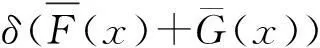
应用引理3可知定理2成立。

定理3在定理1成立的前提下，如果EYα<1且Eln(X-∨1)<∞，则n→∞，有

(18)

证明方法与定理2类似，主要是证明Pr(S∞>x)的渐近上界。

注记4在定理2和3中，若φ(x)=1-2F(x),φ(y)=1-2G(y),则定理2和3即为文献[11]中对应的注记2.1(b),(c)。

下面是推得的破产概率的另一种渐近表达式。

定理4设{(X,Y),(X1,Y1),…,(Xn,Yn)}是独立同分布随机对序列，且随机对(X,Y)服从二元Sarmanov 相依分布，如果EYα+ε<∞,ε>0，则

(19)

证明由Breiman’s定理[4]可得

再根据文献[10]定理4.1即可得证。显然，定理4的精确度要低于定理1。

注记5在定理4成立的前提下，如果EYα+ε<1,ε>0，则

(20)

参考文献：

[1]NYRHINE H.On the ruin probabilities in a general economic environment[J].Stochastic Processes and Their Applications,1999,2:319-330.

[2]NORBERG R.Ruin problems with assets and liabilities of diffusion type[J].Stochastic Processes and Their Applications,1999,81(2):255-269.

[3]VERVAAT W.On a stochastic difference equation and a representation of nonnegative infinitely divisible random variables[J].Advances in Applied Probability,1979,11(4):750-783.

[4]TANG Q,TSITSIASHVILI G.Precise estimates for the ruin probability infinite horizon in a discrete-time model with heavy-tailed insurance and financial risks[J].Stochastic Processes and Their Applications,2003,108(2):299-325.

[5]TANG Q,TSITSIASHVILI G.Finite-and infinite-time ruin probabilities in the presence of stochastic returns on investments[J].Advances in Applied Probability,2004,36(4):1278-1299.

[6]CHEN Y,XIE X.The finite time ruin probability with the same heavy-tailed insurance and financial risks[J].Acta Mathematicae Applicatae Sinica (English Series),2005,21(1):153-156.

[7]ZHANG Y,SHEN X,WENG C.Approximation of the tail probability of randomly weighted sums and applications[J].Stochastic Processes and Their Applications,2009,119(2):655-675.

[8]CHEN Y.The finite-time ruin probability with dependent insurance and financial risks[J].Journal of Applied Probability 2011,48(4):1035-1048.

[9]YI L,CHEN Y.Approximation of the tail probability of randomly weighted sums of dependent random variables with dominated variation[J].J Math Anal Appl.,2011,376(1):365-372.

[10]YANG Y,WANG Y.Tail behavior of the product of two dependent random variables with applications to risk theory[J].Extremes, 2013,16(1):55-74.

[11]LI J,TANG Q.Interplay of insurance and financial risks in a discrete-time model with strongly regular variation[J].Bernoulli,2015,21(3):1800-1823.

[12]杨洋,王开永.保险风险管理中的破产渐近分析[M].北京：科学出版社,2013.

[13]CHEN Y,LIU J,LIU F.Ruin with insurance and financial risks following the least risky FGM dependence structure[J].Insurance:Mathematics and Economics,2015,62:98-106.

[14]崔建斌,付桐林,杨明霞.保险风险和金融风险重尾分布下的二维破产概率的估计[J].曲阜师范大学学报,2013(1):13-17.

[15]颜荣芳,潘欢.重尾环境下二维风险模型在有限时间内的破产概率[J].兰州大学学报(自然科学版),2008(2):119-123.

(责任编辑何杰玲)

The Probability of Ruin Following the Sarmanov Dependence Distribution

WEN Li-yi，GUO Xiao-li

(School of Mathematics and Statistics, Chongqing University of Technology，Chongqing 400054, China)

Abstract:Considering a discrete time insurance risk model with insurance and financial risks, we assumed that both the distributions of insurance and financial risk belong to the strongly regular variation and follow the Sarmanov dependence structure, we derived some precise asymptotic formulas for these probabilities with both finite and infinite time horizons.

Key words：Sarmanov dependence; insurance risk; financial risk; ruin probability

文章编号：1674-8425(2016)04-0147-07

中图分类号：O211.9

文献标识码：A

doi:10.3969/j.issn.1674-8425(z).2016.04.025

作者简介：文丽壹(1989—),男,重庆武隆人,硕士研究生,主要从事应用数学研究。

基金项目：国家社会科学基金资助项目(14BJY200)

收稿日期：2015-10-16

引用格式：文丽壹，郭晓莉.基于Sarmanov相依分布的破产概率研究[J].重庆理工大学学报(自然科学)，2016(4):147-153.

Citation format：WEN Li-yi，GUO Xiao-li.The Probability of Ruin Following the Sarmanov Dependence Distribution [J].Journal of Chongqing University of Technology(Natural Science)，2016(4):147-153.