一种新颖的低复杂度稀疏信道估计算法实现

［苏艳涛　檀童和　李志立］

新技术·新业务

一种新颖的低复杂度稀疏信道估计算法实现

［苏艳涛檀童和李志立］

摘要在无线通信中，信道估计是获取精确接收信号的重要技术。近年来，一种新的方法：压缩感知(Compressed Sensing, CS)，被用来估计信道。与传统的信道估计相比，它大大减少了导频的使用，提高了系统的频谱利用率。但是，CS的高计算复杂度使得它很难应用到实际中。虽然正交匹配追踪(Orthogonal Matching Pursuit, OMP)的提出减少了CS的计算复杂度，但是它的执行效率仍然较低。因此，文章将广义的OMP(Generalized Orthogonal Matching Pursuit, GOMP)算法应用到信道估计中，通过高效的原子选择实现算法复杂度的降低，同时保证信道估计的精度。仿真结果证明了它的有效性。

关键词：信道估计 压缩感知 计算复杂度 原子 重建

苏艳涛

男，重庆邮电大学通信与信息工程学校硕士研究生，主要研究方向基于压缩感知的无线信道估计。

檀童和

男，重庆邮电大学通信与信息工程学校硕士研究生，主要研究方向路网位置隐私保护算法。

李志立

男，重庆邮电大学通信与信息工程学校硕士研究生，主要研究方向信号检测与无线定位。

引言

由于地理环境的复杂性和无线信道的多变性，无线信号在传输的过程中可能会经历多径传播和多普勒频移，进而引起频率选择性衰落和时间选择性衰落。为了在接收端获得精确的接收信号，需要计算准确的信道状态信息(Channel State Information, CSI)，为此，必须预先估计信道冲击响应(Channel Impulse Response, CIR)。目前，获得CIR最常用的方法是基于参考信号或者导频的信道估计方法。

传统的基于导频的信道估计方法有最小二乘法、最小均方误差(Minimum Mean-squared Error, MMSE)法和离散傅里叶变换(Discrete Fourier Transform, DFT)法。传统的信道估计方法没有利用信道的稀疏性，造成频谱资源的浪费。随着研究的不断深入，大量文献表明，无线信道本身往往呈现出稀疏性。基于CS的信道估计利用了无线信道的稀疏性，提高了系统的频谱利用率。截止到目前，针对基于CS的信道估计，已经出现了很多算法：基于l1范数最小化的基追踪(Basis Pursuit, BP)算法[1]、基于贪婪迭代思想的匹配追踪(Matching Pursuit, MP)算法和OMP算法[2-3]等。其中OMP算法具有重构精度高、计算速度快的优点。

近年来，国内外的研究者把研究重点放在了信道估计精度的提高上。针对超宽带（Ultra Wideband， UWB）信道，A.H. Muqaibel提出了与实际场景更加接近的稀疏字典，通过提高超宽带信道的稀疏度来提高接收信号的精度[4]；Baohao Chen将卡尔曼滤波应用到了信道估计中，从而达到了提升估计性能的目的[5]；此外，还有很多研究者通过最佳化导频设置来达到提高估计精度的目的[6-7]。

实际上，利用目前已经出现的信道估计算法，信道估计的精度已经达到很高的水平，算法的复杂度已经成为其走向实际应用的最大障碍。然而，截止到目前，只出现了很少的文献是关于复杂度减少的。文献[8]提出了一个改进的OMP算法（MOMP），在保证信道估计精度的同时减少了算法复杂度，然而它假设信道的抽头具有紧密性，这对于实际用于具有局限性；文献[9]针对稀疏信道估计提出了一个基于压缩感知的扩展图，使得计算复杂度减少到了，其中M是导频数量，N是信道长度，但文献[9]的算法容易受到噪声影响。

前面提到的OMP算法具有重构精度高、计算速度快的优点，但是对于实际应用来说，其计算复杂度仍然较高。为获得更加高效的信道估计，本文提出将GOMP算法[10]应用到稀疏信道估计中来。GOMP算法是OMP算法的改进算法，通过在每次迭代的过程中选取多个原子来大幅度提高算法的运算速度，同时较好的保证信道估计的精度。实验仿真验证了GOMP算法在估计精度和复杂度方面的有效性。

在本文里，粗体的大写字母和小写字母分别表示矩阵和向量；AT是由矩阵A的各列组成的子矩阵，对应于集合T中的各元素；分别表示矩阵A的共轭转置和转置；表示的l2范数；A, h表示向量h与矩阵A做内积运算；hˆ表示向量h的估计。

1　压缩感知理论

压缩感知理论的提出是信号处理领域的一次革命性突破，它打破了奈奎斯特采样定理对数据处理的束缚，大大提高了系统效率。CS理论的应用前提是信号具有稀疏性，即在一组观测信号中，只有很少一部分是非零值或者占优势的值。大量的研究和观测数据表明，无线信道本身往往呈现出很强的稀疏性，这为CS应用到信道估计中奠定了基础。下面给出标准的CS测量模型：

引理1：对任意K稀疏向量t，如果存在一个常数δK∈(0,1)，使得

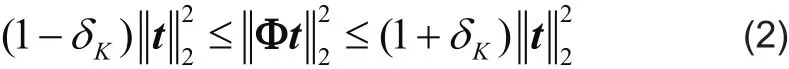
在本文所提的算法中，测量值的个数M是一个很重要的因素。Tropp和Gilbert通过大量仿真得出结论：当

满足(3)式时，运用OMP算法就可以以很大的概率将t从(1)式中重构出来[12]。

2　问题陈述

我们考虑一个长度为N，稀疏度为K的稀疏信道，发送导频个数为M，它们的位置用表示，则基于CS的稀疏信道估计关系式可表示为

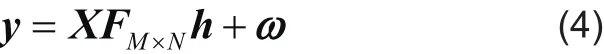
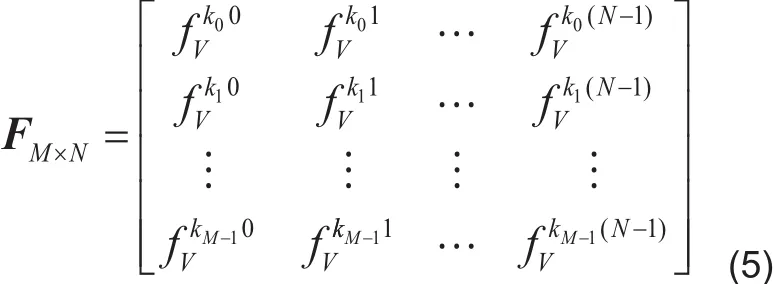
这里，A=[ a1, a2,L, aN]是一个M× N的矩阵，其中ai是A的列向量，对比式(1)可以看出：y，A，h就是CS理论中的测量值，测量矩阵和稀疏信号。获得接收导频向量y之后，采取一定的恢复算法，就可以将信道h从y中恢复出来。

我们采用OMP算法对信道h进行重建。OMP算法是贪婪算法的一种，它可以从观测值中高效稳定的将稀疏信号恢复出来。OMP算法的核心思想是使残差rt最小，在每次循环迭代中采用贪婪策略选择原子然后根据选择的原子集合AΛt进行稀疏重建和残差更新。一般算法循环K次，即可获得原信号的稀疏重建。表1是OMP算法的执行步骤。

仔细研究表1中的OMP算法可以发现，整个算法的关键在于寻找信道h的K个非零值对应的原子，即匹配原子，只要这K个匹配原子找到了，通过步骤③的最小二乘估计就可实现h的精确重建。OMP算法的大部分时间都消耗在了寻找匹配原子，即步骤①上。它的效率非常低，我们用(7)式进行说明

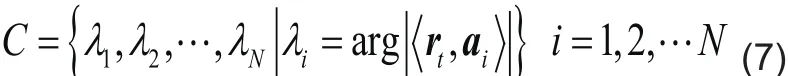
这里，C是一个包含N个引脚的集合，一个引脚对应一个原子。由于N值往往比较大，因此通过算法1中的步骤①做N次相关获得C会消耗比较多的时间。然而OMP算法并没有充分利用C中的N个引脚，而是只取其中最大的一个，把其他引脚完全舍弃，这样不仅浪费资源，而且使得算法收敛较慢。随着算法循环迭代次数的增加，OMP算法的缺点更加凸显出来。

表1　算法1

3　GOMP算法

为了解决OMP算法收敛慢的缺点，本文将GOMP算法应用到稀疏信道估计中。不同于OMP算法，GOMP算法在每次循环迭代中选取n (n 1≥)个原子，即从C中选取前n个最大值的引脚，然后根据选取的原子进行稀疏估计和残差更新。这样，我们不仅充分利用了引脚集合C，而且加快了算法收敛，从而从整体上提升算法的运行效率。关于n的取值，我们给出引理2。

引理2：在GOMP算法中，假设每次迭代选择n个原子，则当n满足(8)式所示的关系时，GOMP算法可以实现原稀疏信道的重建[10]。

这里，K和M分别是信道的稀疏度和导频的个数。

GOMP算法的具体实现如表2。

为了方便理解，我们给出GOMP算法执行的示意图，如图1。

由图1可知，GOMP算法的信道重建也是一个循环迭代过程。由于GOMP算法每次迭代选取n个原子，因此一般情况下算法循环K/ n次即可完成原稀疏信道的精确重建，这大大缩短了运行时间，提高了算法的执行效率。

表2　算法2

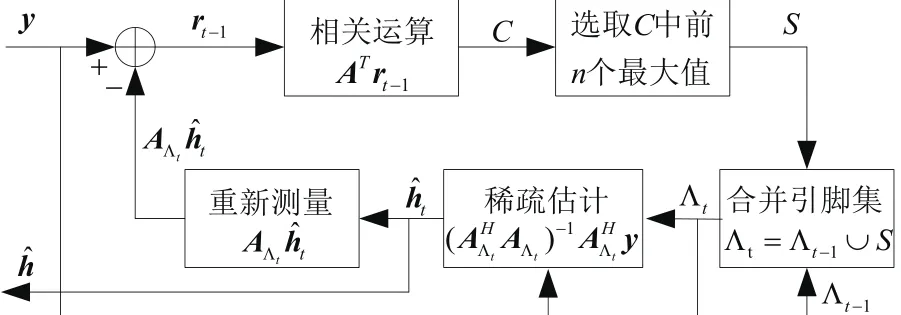
图1　GOMP算法

4　仿真分析

为了证明所提算法的有效性，我们给出算法的均方误差(Mean Square Error, MSE)仿真和运行时间仿真，并与传统的LS算法、MMSE算法、OMP算法作比较，随后给出算法的复杂度分析。

4.1MSE仿真

考虑一个长度为N =496，稀疏度为K =12的稀疏信道。导频采用高斯导频，为了保证信道的精确重建，选取M =256。噪声采用复高斯白噪声。此外，考虑到引理2，令原子选择个数分别为n =2,5,9。仿真中采用归一化的MSE，结果如图2和图3。

图2是在不同的信噪比下，各个算法的MSE性能仿真。从图中可以看出，随着信噪比的增大，各算法的MSE逐渐下降，即信道重构的精度越来越高。与传统的算法相比，GOMP算法的重构精度不仅远远好于LS算法，而且与OMP算法很接近。甚至在n =2时，GOMP算法完全可以和OMP算法相媲美。这证明了我们提出的算法在估计精度方面的有效性。

图3是在稀疏度发生变化的情况下，各算法的MSE性能仿真。从图中可以看出，随着K值的不断增大，信道估计的精度越来越低。这是由于随着K的增加，信道变得越来越不稀疏，而导频的数目却没有随之增加，导致我们不能获得足够的信道信息，从而导致估计误差的增大。值得注意的是，随着K值的增加，虽然算法的性能出现了下降，但是GOMP算法却一直很好的“跟随”了OMP算法，这表明GOMP算法在不同的稀疏度下具有稳健性。此外，虽然在图2和图3中MMSE算法的估计精度最好，但由于其计算复杂度过大，实际中一般不采用。我们可以将MMSE算法的MSE曲线作为估计精度的下限。

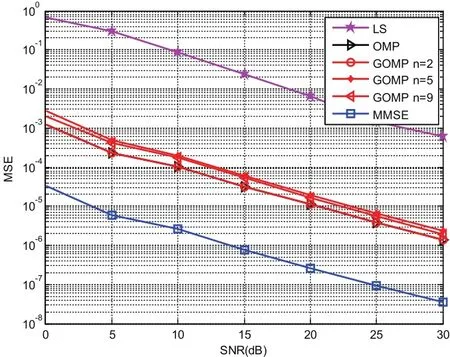
图2　不同信噪比下的MSE性能比较

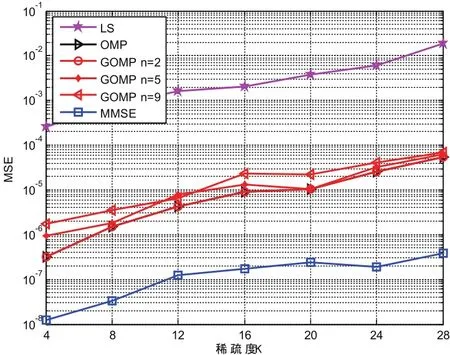
图3　不同稀疏度下的MSE性能比较

4.2运行时间仿真

这一节，我们给出算法的运行时间仿真。仿真参数设置为：SNR= 5dB，M =512，K =12。仿真结果如图4。由于MMSE算法的复杂度太大，因此仿真中没有考虑MMSE算法。

由图4可以看出，GOMP算法在运行时间上具有良好的表现。其中GOMP(n = 5,9 )只占了OMP算法运行时间的近1/ 2，也就是说它可以节约超过50%的时间。随着信道长度的增加，GOMP算法的优越性更加明显。

此外，我们给出算法的平均迭代次数仿真，如图5。从图中可以看出，在不同的稀疏度下，GOMP算法的迭代次数都少于OMP算法。由于算法的复杂度与迭代次数密切相关，因此图5的仿真结果不仅再次证明了GOMP算法在复杂度方面的优越性，而且还证明了算法在不同的稀疏度下具有稳健性。

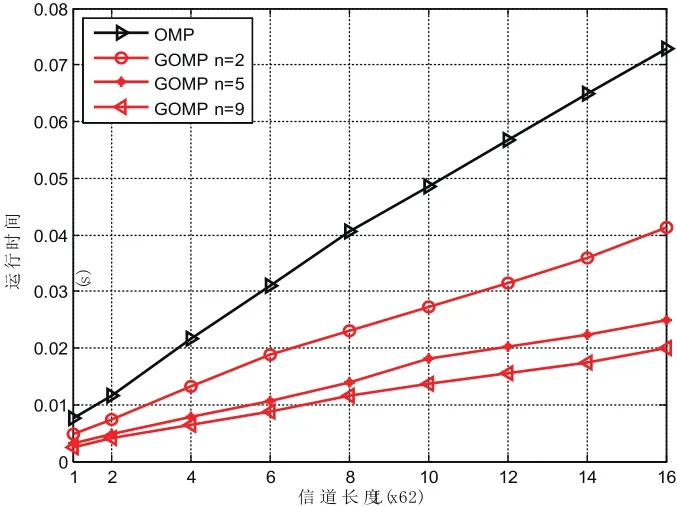
图4　同信道长度下的运行时间比较

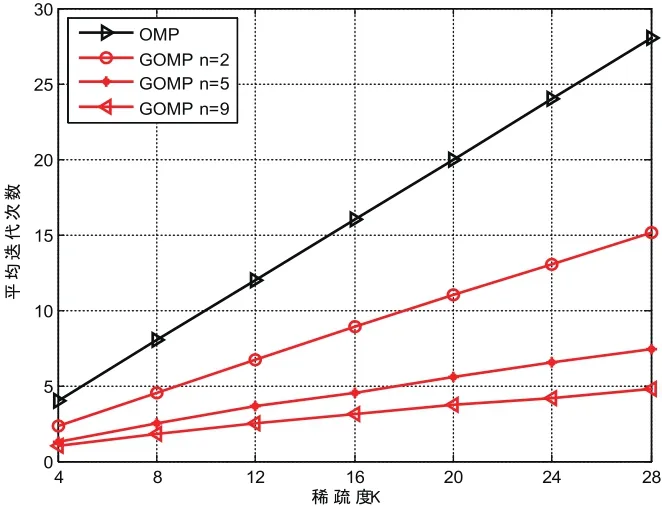
图5 不同稀疏度下的迭代次数比较

综合以上仿真可以看出，针对GOMP算法，当n值越小，信道估计的精度越高，但算法的执行效率却越低；当n值越大，算法的执行效率越高，但算法的估计精度却越低。因此在实际应用中，我们要根据估计精度和运行效率的实际需求来适当地选取n值。

4.3复杂度分析

这一节，我们给出GOMP算法的复杂度分析，从理论层面证明算法的优越性。文献[10]指出，GOMP算法的复杂度可近似地表示为，其中s为迭代次数。由于OMP算法是GOMP算法在n =1时的特殊情况，因此OMP算法的复杂度可以表示为：

在GOMP算法中，迭代次数s和原子选择个数n都比较小，因此其复杂度可以记作O( sMN )，而OMP算法的复杂度为O( KMN )。从图5可以看出s往往比K小很多，也就是说，GOMP算法在计算复杂度方面更具有优越性。

5　结论

本文针对现有的信道估计方法计算复杂度较大的问题，提出将GOMP算法应用到稀疏信道估计中去。受益于有效的原子选择方法，GOMP算法不仅具有良好的估计精度，而且可以大大降低信道估计所需的时间。特别是GOMP(n = 5,9 )可以实现节约50%以上的运行时间，计算机仿真和理论分析证明了它的有效性。因此，GOMP算法很有希望成为未来无线通信中信道估计的备选方案。

参考文献

1Jianzhong Huang, C. R. Berger, Shengli Zhou. Comparison of basis pursuit algorithms for sparse channel estimation in underwater acoustic OFDM [C]. OCEANS 2010 IEEE, 2010: 24-27

2Teng Sun, Zhiqun Song, Yongjie Zhang. Matching pursuit based sparse channel estimation using pseudorandom sequences [C]. Millimeter Waves (GSMM), 2012 5th Global Symposium on. IEEE, 2012: 33-37

3N. Aboutorab, W. Hardjawana, B. Vucetic. Application of compressive sensing to channel estimation of high mobility OFDM systems [C]. Communications (ICC), 2013 IEEE International Conference on. IEEE, 2013: 4946-4950

4A.H. Muqaibel, M.T. Alkhodary. Practical application of compressive sensing to ultra-wideband channels [J]. Communications, IET, 2012, 6(16): 2534-2542

5Baohao Chen, Qimei Cui, Fan Yang. A novel channel estimation method based on Kalman filter compressed sensing for time-varying OFDM system [C]. Wireless Communications and Signal Processing (WCSP), 2014

Sixth International Conference on. IEEE, 2014: 1-5

6Jungchieh Chen, Chaokai Wen, Pangan Ting. An efficient pilot design scheme for sparse channel estimation in OFDM systems [J]. Communications Letters, IEEE, 2013, 17(7): 1352-1355

7Xiang Ren, Wen Chen, Meixia Tao. Compressed channel estimation with joint pilot symbol and placement design for high mobility OFDM systems [C]. High Mobility Wireless Communications (HMWC), 2014 International Workshop on. IEEE, 2014: 38-42

8Ziji Ma, Hongli Liu, T. Higashino. Low-complexity channel estimation for ISDB-T over doubly-selective fading channels [C]. Intelligent Signal Processing and Communications Systems (ISPACS), 2013 International Symposium on. IEEE, 2013: 114-118

9Junjie Pan, Feifei Gao. Efficient channel estimation using expander graph based compressive sensing [C]. Communications (ICC), 2014 IEEE International Conference on. IEEE, 2014: 4542-4547

10Jian Wang, Seokbeop Kwon, Byonghyo Shim. Generalized orthogonal matching pursuit [J]. Signal Processing, IEEE Transactions on, 2012, 60(12): 6202-6216

11E. J. Candes. The restricted isometry property and its implications for compresses sensing [J]. Comptes Rendus Mathematique, 2008, 346(9): 589-592

12J. A. Tropp, A. C. Gilbert. Signal recovery from random measurements via orthogonal matching pursuit [J]. Information Theory, IEEE Transactions on, 2007, 53(12): 4655-4666

DOI:10.3969/j.issn.1006-6403.2016.01.005

收稿日期：（2015-12-08）