多层屈曲约束斜撑钢框架抗震性能研究

陈宜虎, 赵艳林, 包恩和, 张　敏

(1. 广西大学 土木建筑工程学院， 广西 南宁 530004； 2． 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004；3. 桂林理工大学 博文管理学院， 广西 桂林 541006)



多层屈曲约束斜撑钢框架抗震性能研究

陈宜虎1,2，3, 赵艳林1, 包恩和2, 张敏2

(1. 广西大学 土木建筑工程学院， 广西 南宁 530004； 2． 桂林理工大学 土木与建筑工程学院， 广西 桂林 541004；3. 桂林理工大学 博文管理学院， 广西 桂林 541006)

摘要：为研究多层屈曲约束斜撑钢框架(buckling restrained braced frame, BRBF)的弹塑性动力性能，采用刚接与铰接两种形式的模型为研究对象，以屈曲约束斜撑(buckling restrained brace, BRB)水平力分担率平均值β和首层剪重比CB为主要研究参数，通过弹塑性动力二阶非线性分析，探讨了BRBF结构的抗震性能.结果表明：在设防烈度地震下最大层间位移各层分布较均匀；罕遇和特大地震下,刚接模型除首层和顶层外各层集中，铰接模型因柱脚铰接首层特别大，另外受第二振型影响中上层也较大.强震作用下，β≈30%时，结构以剪切变形为主，第一振型卓越；β≈60%时，第二振型参与；β≈90%时，第二振型卓越.结构基本周期一定时，β值大小不影响地震输入总能量；模型基本周期相近时，结构等效速度VE基本相等；同时，β值可从结构弹性基本周期以及地震波弹性体系能量谱中得到推算，再次验证了基于能量平衡抗震设计法的有效性.

关键词：屈曲约束斜撑水平力分担率平均值； 高阶振型； 构件需求性能； 能量设计法

近年来国内外开发和研究了各式各样的耗能减震器[1]，其中屈曲约束支撑(BRB)因其耗能性能好，制作、施工简便，而被广泛应用[2].同时，关于屈曲约束斜撑钢框架(BRBF)的研究也不在少数：文献[3]以BRB与主体结构刚度比作为主要参数研究了BRB的优化布置；文献[4-6]基于能量平衡规律研究了BRBF结构的抗震设计法；而强震作用下较详细的多层BRBF结构的抗震性能研究却相对较少.文献[7-9]采用国际上最常见的两种多层BRBF结构形式为研究对象，以BRB水平力分担率平均值β(β的定义见式1)为主要研究参数，通过弹塑性静动力分析，从楼层静动力响应方面着手，着重探讨了不同β值对各层层间位移、层剪力的影响，层损伤分布机理的研究.文献[9]指出，强震作用下多层BRBF结构当β=90%时，采用底部剪力法作结构静力设计时，基于能量平衡准则无法准确评价层间位移反应值；同时，β与BRB需求性能(变形和耗能)关系尚不明确.

作为对前述研究的深化，以β作为主要研究参数之一，且考虑到地震输入的总能量主要取决于结构的重量和基本周期[10]，为研究模型基本周期对地震输入总能量及结构地震反应的影响程度，设定各模型同一层的重量相等，并设定首层剪重比CB≈0.3和0.5(CB=Qu/W,Qu为静力分析最大层间位移角等于1/50时首层剪力；W为结构总重量)，通过二阶非线性时程分析，研究β值、基本周期和地震卓越周期的变化对层间位移反应值的影响，基本周期对地震输入能量的影响；并进一步研究多层BRBF结构中，β对BRB需求性能和结构振型的影响.

1研究模型

模型各层重量分布：首层3 550 kN、顶层3 200 kN，标准层3 480 kN；各模型首层剪重比CB≈0.3和0.5，β值分别在30%,60%和90%左右.

刚接连接形式中，因箱型截面柱于X，Y向整体刚度、强度分布均匀，且结构超静定次数高，抗震性能优越，被广泛应用于日本、中国台湾和大陆等地.β在30%和60%时，柱、梁以及柱脚均为刚接，定义为刚接模型(Rigid Model， RM).β=90%时，外围中间跨柱与梁为刚接，其他构件的连接均为铰接，即内部柱梁连接为铰接，外侧框架梁柱一个方向刚接、一个方向铰接，定义为铰接模型(Pinned Model， PM)，为美国框架主要采用形式；此种连接H型截面柱强轴受弯方向与梁刚接，弱轴与梁铰接，地震时因框架内部林立的柱子穿过各层楼板起连续梁作用，增强了层间相互作用，能够较好控制特定层的层间位移，形成全层机制.

考虑到文章篇幅，将RM和PM模型各一半对称绘制于Y向对称符号两侧，平立面布置及梁、柱、支撑连接见图1和图2.

图1　标准层平面图

图2　BRBF计算简图

模型的命名按模型形式β值×10首层剪重比×10表示，即RM33，RM35，RM63，RM65，PM93和PM95，如RM35代表Rigid Model，β=30%，首层剪重比为0.5.

BRB水平力分担率平均值β定义如下：

(1)

(2)

式中，βi，Qbi和Qi分别表示，达到设计层剪力时，第i层支撑水平力分担率平均值，第i层支撑分担的剪力和第i层的层剪力，n为层数.

各框架的强柱系数α均大于1，强柱系数α表达为

(3)

式中:B-CMp(i)为i层柱脚全截面塑性弯矩;T-CMp(i-1)为i-1层柱头全截面塑性弯矩；L-BMp(i)和R-BMp(i)分别为i层梁左、右端全截面塑性弯矩.

PM模型柱选用H型截面，梁和BRB均为H型截面.各模型经非线性分析软件[11]计算得到的主要参数和用钢量如表1所示.

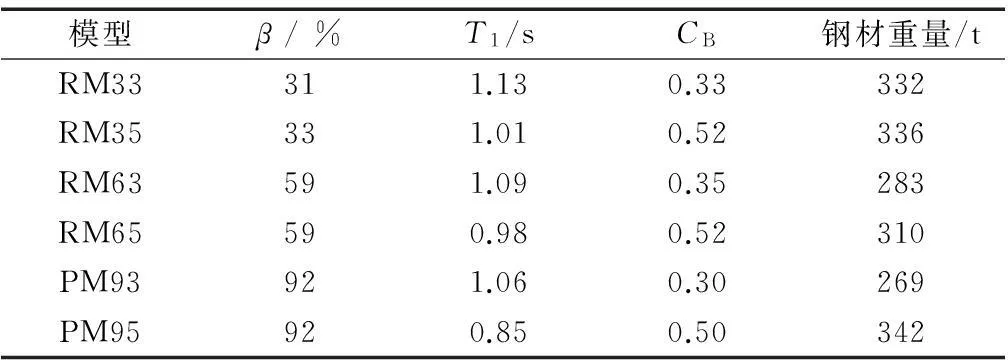
表1　分析模型的主要参数

注：β为设计层剪力时各层(BRB)水平力分担率平均值；T1为结构基本周期；CB为首层剪重比.

2结构动力弹塑性分析

2.1分析方法

结构时程分析微分方程

(4)

式中:{pH,t+△t}和{pv,t+△t}分别是水平与竖向地震作用力，如式(5)

(5)

基于楼板水平刚度远大于BRBF，以及BRBF结构的对称性，使用能够考虑几何非线性、材料非线性等的二阶非线性分析程序，对各模型进行时程分析，详细的计算原理见文献[11].该分析程序建模时，将空间框架简化成各自独立的单榀平面框架，并通过铰接刚性连梁的连接实现空间模型的平面拼接.因此，采用铰接刚性连梁一端连接X1轴平面框架，另一端连接X2轴平面框架，以实现程序用平面模型模拟三维模型的简化，如图2.由Y向次梁(the Second Beam)传给主梁的荷载P2和P4，Y向主梁传给柱的荷载P1和P3以集中力的形式作用于相应主梁跨中和各层柱顶；各构件恢复力模型为双线型，其屈服后的刚度为初刚度的1/100；框架阻尼矩阵，采用阻尼系数2%的刚度比例型.

地震波选用El Centro NS 和 Taft EW波，其强度等级按照地动最大速度值划分为三个等级，分别对应于：常遇地震，地动最大速度25 cm·s-1；设防烈度地震，地动最大速度50 cm·s-1(用E2和T2表示)； 罕遇地震，地动最大速度75 cm·s-1(用E3和T3表示).本文采用后两个等级进行分析，选择了地动最大速度为91 cm·s-1的JMA Kobe NS的特大地震(用K3表示).各模型时程分析时长均为30 s，具体参数详见表2；E3，T3和K3作用下，当阻尼系数h=5%时弹性体系能量谱(等效速度—周期关系)详见图3，其中研究模型基本周期范围参见表1.

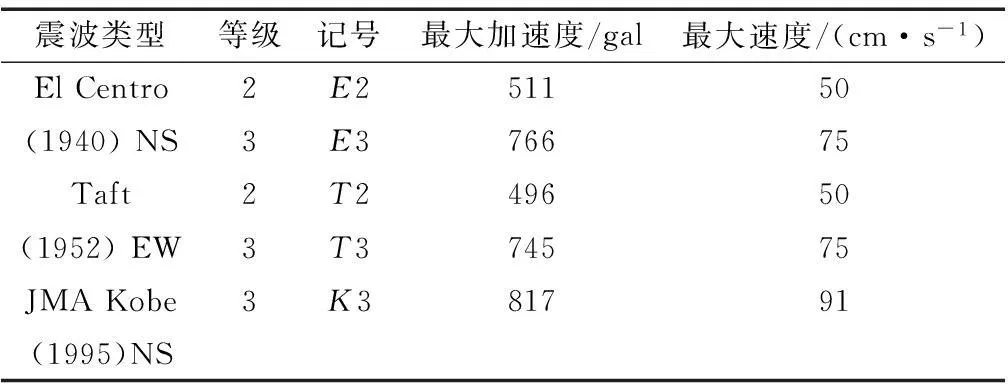
表2　地震波参数

图3　能量谱(等效速度周期关系)

2.2分析结果

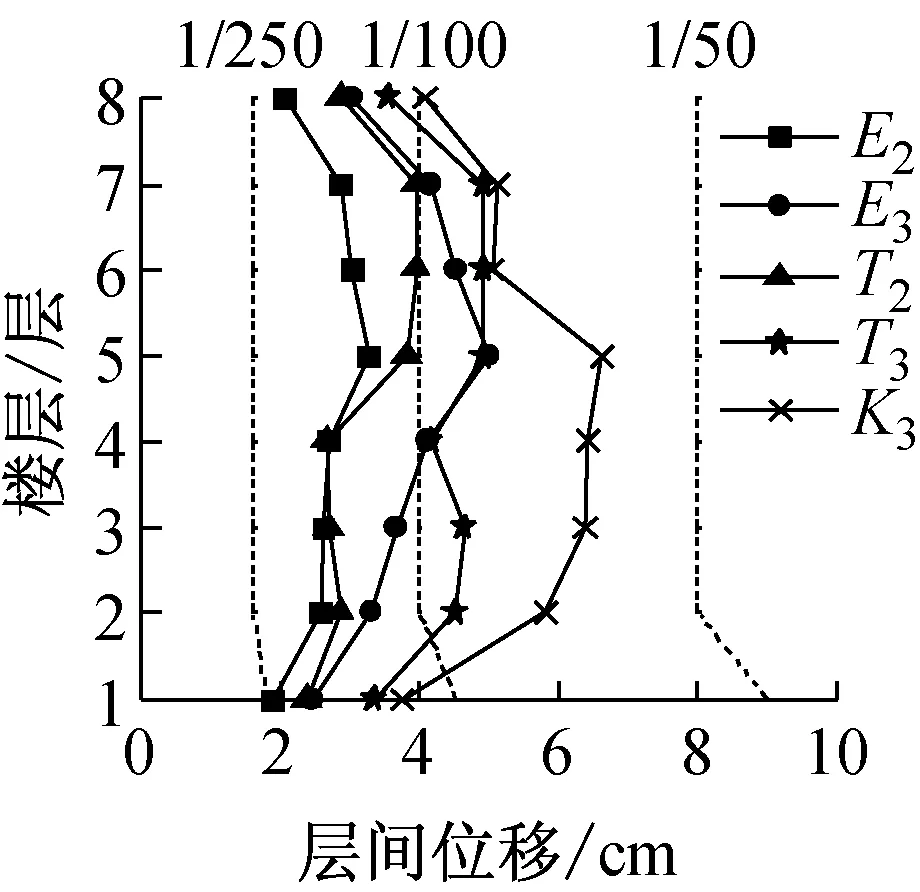
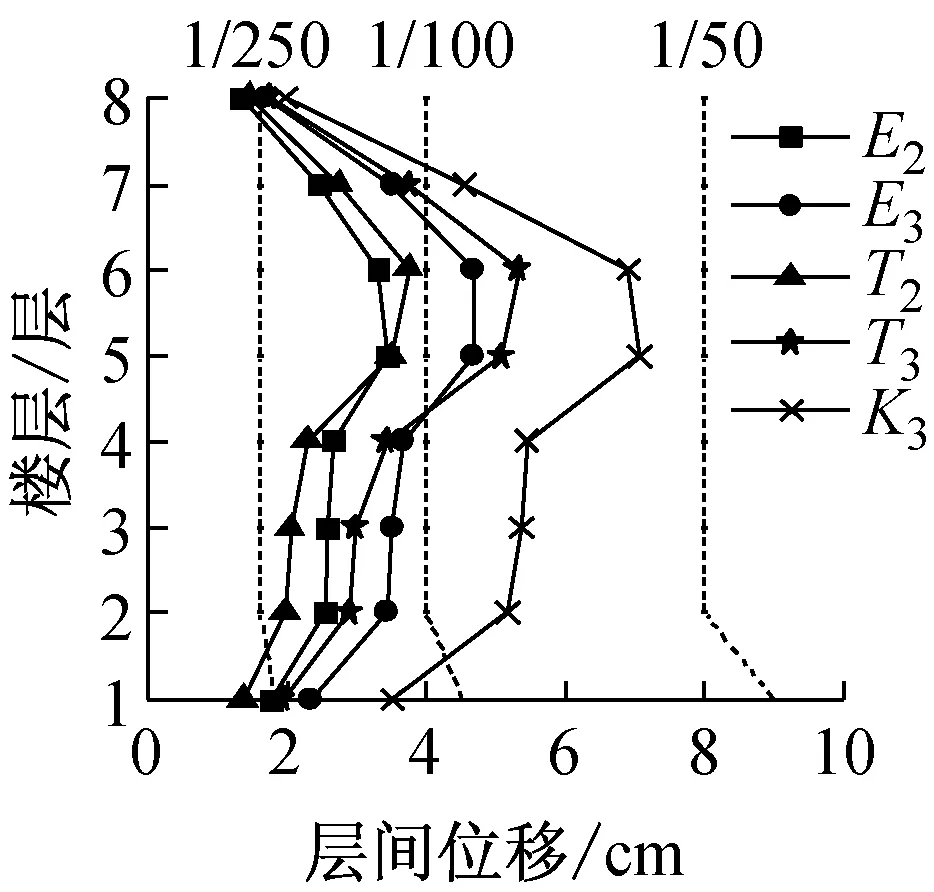
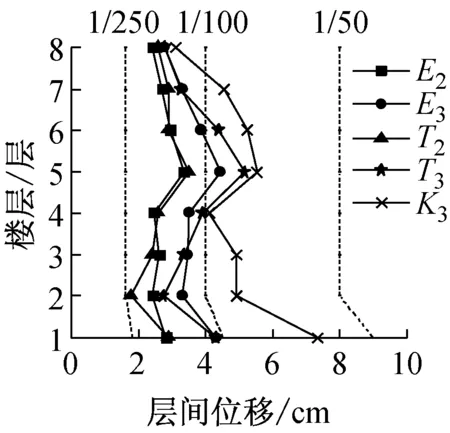
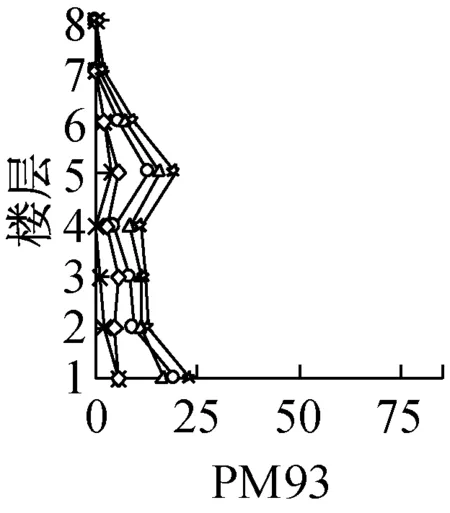
各模型各层的最大层间位移分布如图4所示.地震波等级为2，3级时，RM模型最大层间位移分布首层与顶层较其它层小，5，6层等中间楼层较集中；K3作用下，2～6层层间位移较大.E3，T3和K3作用下，PM模型最大层间位移以首层、5～6层相对较大.分析可知，PM模型因柱脚铰接导致首层损伤较集中，故首层层间位移相对较大；同时，BRB水平力分担率平均值β值在90%左右，强震作用下框架柱轴向伸缩变形量大，PM模型6～8层弯曲变形卓越[7]，一般情况下上层部分层间位移减少，但是，PM模型强震时第二振型卓越见图5c，导致5，6层变形集中.

a RM33

b RM35

c RM63

d RM65

e PM93

f PM95

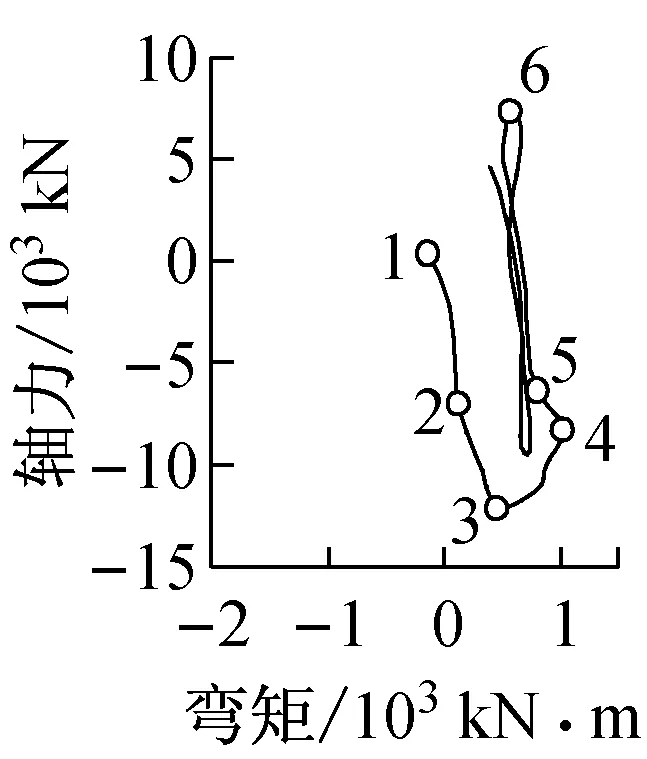
C1柱M-N曲线

B1梁M-N曲线

1层N-Δ关系

5层N-Δ关系

7层N-Δ关系

8层N-Δ关系

C1柱M-N曲线

B1梁M-N曲线

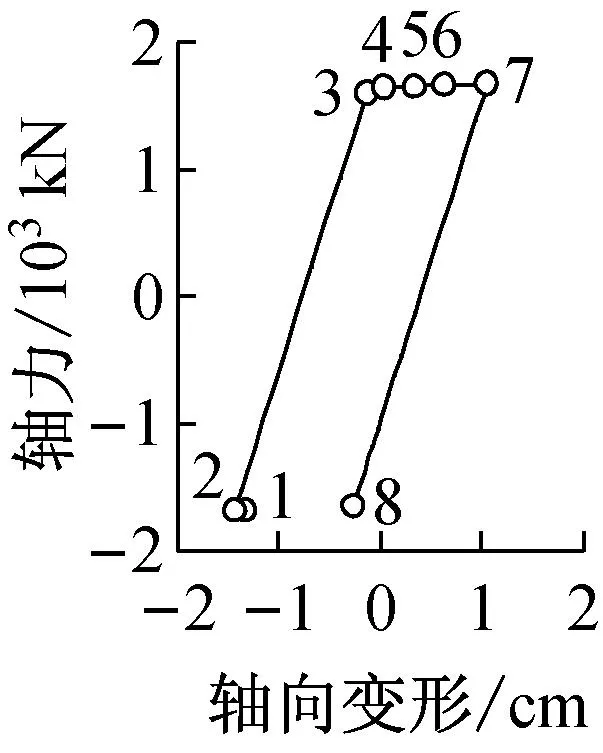
1层N-Δ关系

6层N-Δ关系

7层N-Δ关系

8层N-Δ关系

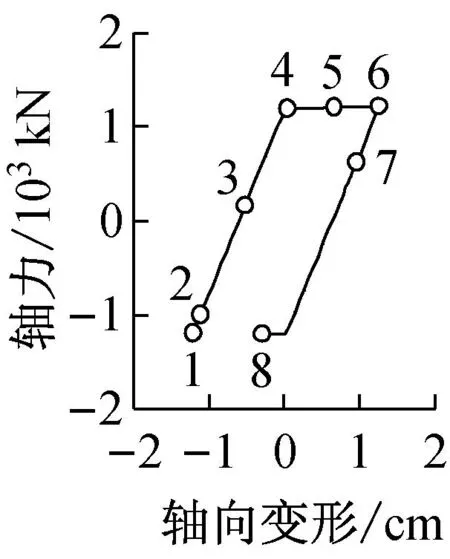
C1柱M-N曲线

B1梁M-N曲线

1层N-Δ关系

5层N-Δ关系

7层N-Δ关系

8层N-Δ关系

各模型最大层间位移角值，E2，T2作用下分布在1/200～1/150范围内；E3，T3时，分布在1/100左右；K3时，1/75左右，并且小于弹塑性层间位移角限值1/50.

各模型最大层间位移，当CB≈0.5时并不全部小于CB≈0.3的对应值；基于位移的抗震设计，BRBF从CB≈0.3增加到0.5不一定能够减少框架损伤，由图3能量谱可知，建筑物基本周期和地震波卓越周期特性的影响更显突出.

2.2.2能量分析

地震波作用下，地震输入总能量可转化为等效速度VE(=(2Et/M)0.5)，详见表3；而地震输入总能量在建筑中又可转换成各构件弹塑性变形能量、建筑阻尼消耗能量以及建筑动能等.即

(6)

式中：Et为地震输入总能量；Ep为柱、梁、支撑等构件塑性变形耗能；Eh为建筑阻尼消耗能量；Ek为建筑运动能量；Ee为柱、梁、支撑等构件弹性变形能量.

1.2.1 对照组。采用传统切割法切除扁桃体：使用尖刀切开上极外侧黏膜，分离扁桃体上极，沿扁桃体被膜分离，直至仅有少量组织连接扁桃体下极后使用圈套器将其完整切除。

表3　总输入能量的等效速度VE

Housner和秋山宏指出，地震动给予建筑结构的总输入能量Et是仅仅与结构的总质量和基本振动周期相关的一个比较稳定的量，其值大小不受建筑结构质量分布、刚度分布、强度分布等结构参量的影响[10,12-13].本文中结构同层质量一致，因此，在E2～K3作用下，当模型地震波弹性体系的能量谱确定之后，VE与β值大小、柱脚形式、BRBF结构形式等的单独变化无关，而主要取决于各模型基本周期.从表3也可验证以上表述，当各模型基本周期相近时，同一地震等级下，VE值也基本相等.同时，VE值可从结构弹性基本周期以及地震波弹性体系能量谱得到推算，再次证明了基于能量平衡的抗震设计方法的有效性.

各构件损伤能量的大小和层损伤分布直接影响建筑破坏机制，地震中BRBF所吸收的全部塑性变形能量Ep由BRB和框架各组成构件的塑形受力变形所消耗，用公式表示如下:

(7)

式中：Epb=BRB塑性变形能量；Epf= 柱、梁塑性变形能量.

地震作用下，各模型Ep和Epb/Ep(BRB塑性变形吸收能量分担率) 如表4所示.

表4　BRB塑性能量Epb以及 Epb / Ep

Epb和Epb/Ep跟地震强度等级以及β值有关.地震强度等级2时，各模型Epb/Ep大于96%，框架柱、梁基本能够保持线弹性状态；地震强度等级3时，BRB吸收了大量的塑性能量；除RM33模型的Epb/Ep比值为78%以外，其他模型在地震等级3作用下的Epb/Ep均超过96%；K3作用下，β值越大，BRB吸收的损伤能量分担率及能量绝对值也相应增大，PM模型BRB吸收的损伤能量分担率达到99%以上，框架柱、梁能够保持线弹性状态.

从表4可知，β值未超过30%时，仅有个别Epb/Ep比值低于90%(但也在52%以上)；也就是说，设置数量不多的BRB时(β>30%)，BRB塑性变形吸收能量已达到梁、柱和BRB吸收能量之和的90%以上；同时，结合表2,图4可知，在地震等级2,3作用下，各模型最大层间位移角值均在《建筑抗震设计规范GB50011—2010》规定的多、高层钢结构弹塑性层间位移角限值1/50以下.故各模型BRB的减震效果明显.

2.2.3BRB、BRB连接梁、柱的地震响应

这里分别采用BRB水平力分担率平均值β≈30%，60%和90%的RM33，RM63和PM93模型，探讨β值变化与多层BRBF结构振型的关系.

各模型分析地震波输入时间区段，取在地震波E3作用下，当结构首层层间位移达到最大时，对应的地震波输入时刻点分别向左右各扩散一个建筑物周期时长；在此地震波输入时长区间内RM33,RM63和PM93模型的BRB、BRB连接梁和柱相应响应情况如图5所示.

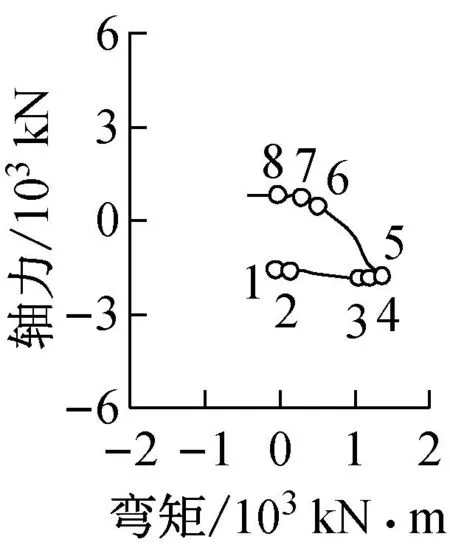
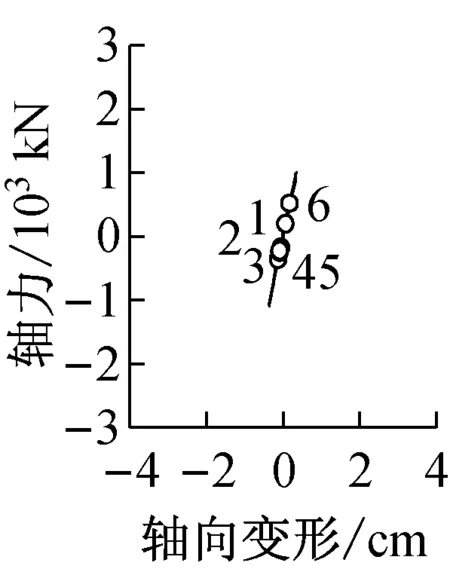
图5a描述了RM33模型在地震输入后2.76～3.36 s间的地震响应，大约在3 s左右时，模型首层层间位移达到最大.

图5a第1，2幅描述了BRB首层连接柱(C1柱)和连接梁(B1梁)的弯矩—轴力关系.图5a中C1柱M—N曲线图8时刻点时C1柱轴力为1 840 kN，达到最大；5时刻点时，其弯矩达到最大值1 360 kN·m.图5a第3～6幅图分别描述了第1，5，7，8层BRB轴力—轴向变形关系，图中相同编号对应地震波入力时刻点一致.1～2时刻段，1—8层BRB处于弹性状态，且该时刻段持续时间较短，首层C1柱和B1梁的轴力、弯矩增幅不大.2～5时刻段，各层的BRB中，仅8层的BRB在2～3时刻段处于弹性状态外，均处于屈服状态；首层C1柱的轴力增幅缓慢，其弯矩却因框架剪切变形卓越而增幅明显，且至5时刻点时弯矩达到最大；3～5时刻段，首层B1梁的轴力不再增加，5时刻后各层BRB开始卸载而进入弹性状态.从各层BRB轴力—轴向变形关系得知，β值30%左右时，RM33模型的振动以基本振型(第一振型)为主.

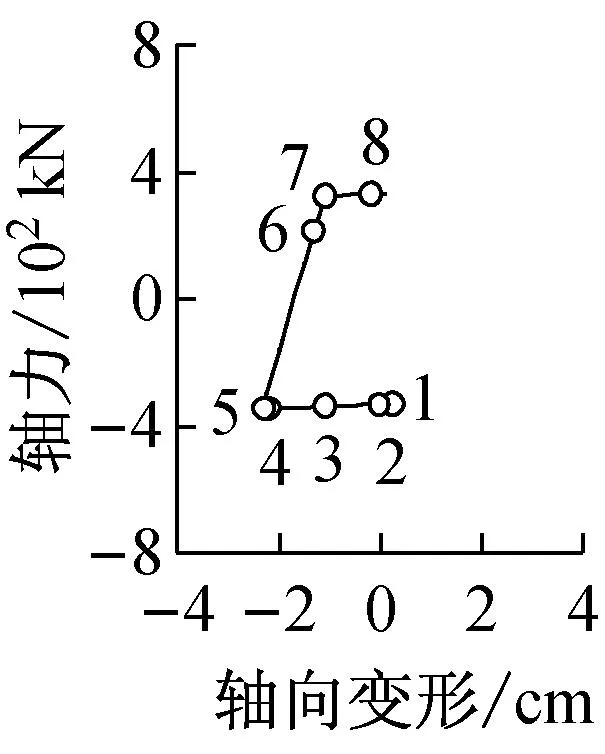
图5b描述了在地震波输入5.34～6.54 s区段内模型RM63的地震反应.图5b第1和第2幅图为C1柱B1梁弯矩—轴力(M-N)关系曲线；图5b第3～6幅图分别为第1,6,7,8层BRB轴力—轴向变形(N-⊿)曲线.

图5b的C1柱M—N曲线图中，1时刻点时C1柱轴力值最大，为7 770 kN；7时刻点时，弯矩值最大，为1 186 kN·m.由图5b的3～6幅图可知，1～3时刻点，首层至8层的BRB处于弹性状态，且与其相连的首层C1柱和B1梁的轴力与弯矩增幅较大.3～4时刻点，1—5层的BRB处于屈服状态，而6～8层的BRB仍处于弹性状态，与BRB相连的C1柱首层轴力稍有增加.4～6时刻点，除第7—8层BRB处于弹性状态，其他层均进入屈服状态，C1柱的轴力有增幅；因β=60%，且C1柱轴力较大，BRBF结构以弯曲变形为主，故弯矩的增幅不明显.6～7时刻点，BRBF结构低、中层部分BRB处于屈服载荷状态(即1—5层)，而BRBF结构高层部分的BRB处于弹性卸除载状态 (即6—8层)；并且BRBF结构低、中层部分与高层部分位移方向相反，BRBF结构的振动已体现了第2振型的参与.

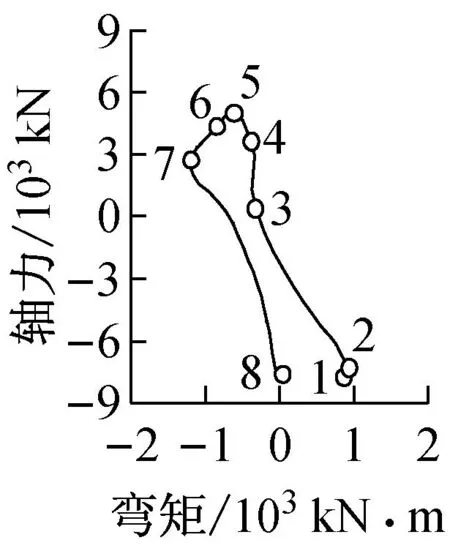
图5c描述了模型PM93当首层层间位移达到最大时，在地震波输入2.7～4.4 s内的BRB、BRB连接梁和柱地震反应过程.图5c第1幅和第2幅图是与BRB相连的首层C1柱和B1梁的弯矩—轴力(M-N)关系曲线；图5c第3～6幅图是1—8层BRB轴力—轴向变形曲线.

图5c的C1柱M—N曲线3 h对应轴力值最大，为12 120 kN、4时刻点弯矩值最大，为1 016 kN·m.1～2时刻点， BRB均处于弹性状态，与BRB相连的C1柱轴力急剧增加，弯矩增幅较小，呈现桁架结构变形特性；与BRB相连的B1梁的轴力也有增加，但于1—2层BRB屈服后，即2时刻点后，其轴力不再增加.2～3时刻点，BRB于1—6层处于屈服状态，7—8层处于弹性状态；因7—8层BRB的附加轴力作用，与BRB相连的C1柱轴力有所增加，且在3时刻轴力值达到最大.3～4时刻点，首层BRB保持屈服状态，而5层则进入弹性卸载阶段，框架低层部分(即1—4层)BRB处于加载阶段，上层部分(即5—8层)处于卸载阶段，且模型低层部分与上层部分BRB变形方向相反，BRBF结构第2振型卓越；因第2振型参与，C1柱弯矩继续增加，并于4时刻点弯矩值达到最大.4～5时刻点，BRB于首层开始进入弹性卸载阶段，且于6时刻点前各层BRB均为弹性受力，BRBF也呈弹性状态.在地震等级2以上的其他地震作用下，PM93模型的振型反应也相同.

综上所述，与BRB相连的首层C1柱和B1梁的最大轴力值与弯矩受各模型β值大小的影响，表现为轴力随着β值的增大而增加，弯矩值却随着β值的增大而减小趋势.

2.2.4各层BRB的延性比μ及累积塑性延性比η分布

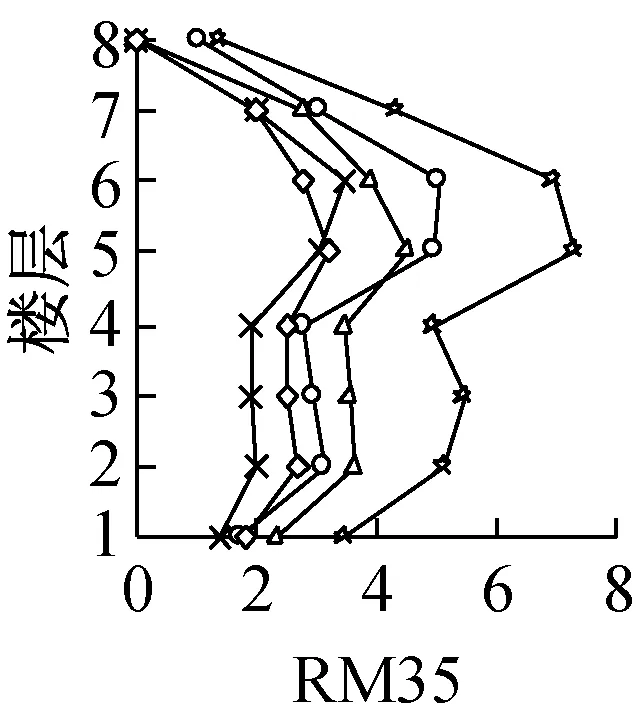
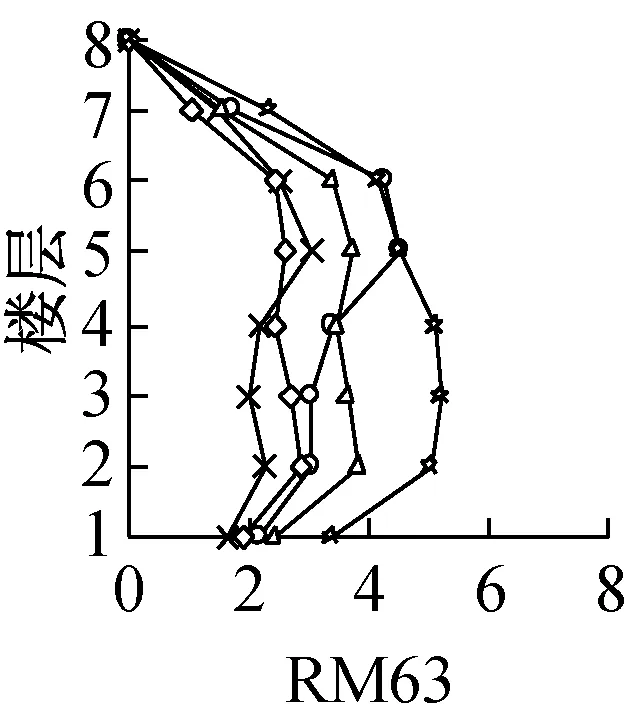
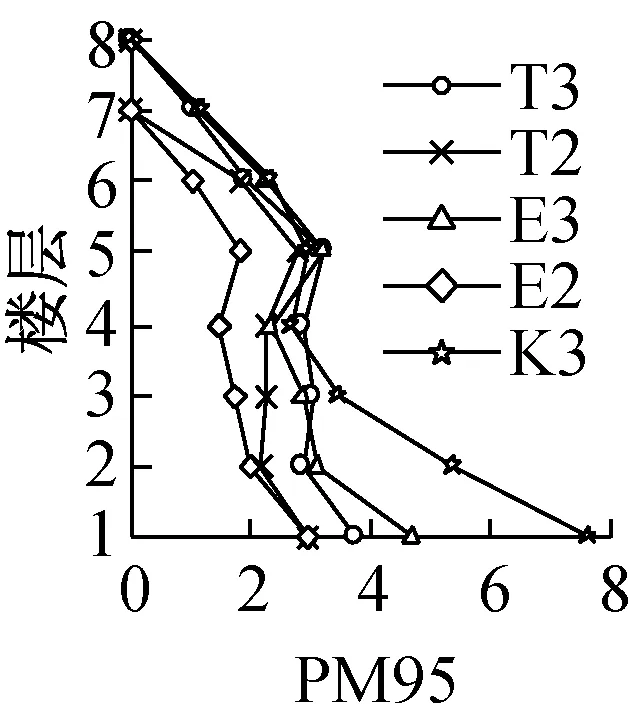
模型RM33,RM35,RM63,RM65,PM93和PM95的各层BRB最大延性比μ和最大累积塑性延性比η分布如图6所示，定义如下：

(8)

(9)

式中：Δmax为BRB的最大轴向变形；⊿y为BRB的轴向屈服变形；⊿p+，⊿p-为BRB的受拉区和受压区塑性轴向变形.

各模型各层BRB最大延性比μ值.K3作用下最大，RM33和RM35模型第5层最大，分别为7和7.2；RM63和RM65第3层最大，分别为5.2和5.9；而PM93和PM95首层为最大，分别为6.8和7.6.比较μ值分布，RM模型2—6层较大，PM模型首层和第5层较大.因PM模型β在90%左右，强震作用下BRB连接柱轴向伸缩变形量大，且BRBF结构上层部弯曲变形卓越，同时因框架柱轴向伸缩变形的累积效应以及柱脚的铰接连接，导致结构损伤集中于底层部；同时，β值大于90%的模型因第二的振型参与 (见图5c第3，4幅图) ，第5，6层的μ值也较大.基本上，CB≈0.5的模型各层μ值大于CB≈0.3的模型，而CB值从0.3增加到0.5不一定能够减少构件的最大变形，因为如图3的能量谱所示，各模型基本周期与地震输入总能量的关系影响尤为突出.

a 最大延性比μ

b 最大累积塑形延性比η

各模型各层BRB最大累积塑形延性比η值.E3作用下，RM33模型第5层、RM63第2层和PM95首层最大，分别为80，29和28；其他模型在K3作用下，RM35模型第5层、RM65模型第2层、以及PM93模型首层最大，分别为54，24.4和23.5.从各模型各层η分布可知，RM模型2—6层较大，而PM93首层和第5层较大，PM95第1，2层较大.总体上，CB≈0.5的模型各层η小于CB≈0.3的模型；分析可知，CB从0.3增加到0.5时，各层BRB截面尺寸变大，其屈服强度和初刚度值增大，瞬间吸收能量增大，因此各层BRB累积塑性变形变小.

由以上分析可知，随着各模型BRB水平力分担率平均值β值的增加，各模型各层BRB最大延性比μ以及最大累积塑性延性比η呈减小趋势，其中η值的变化尤为明显.

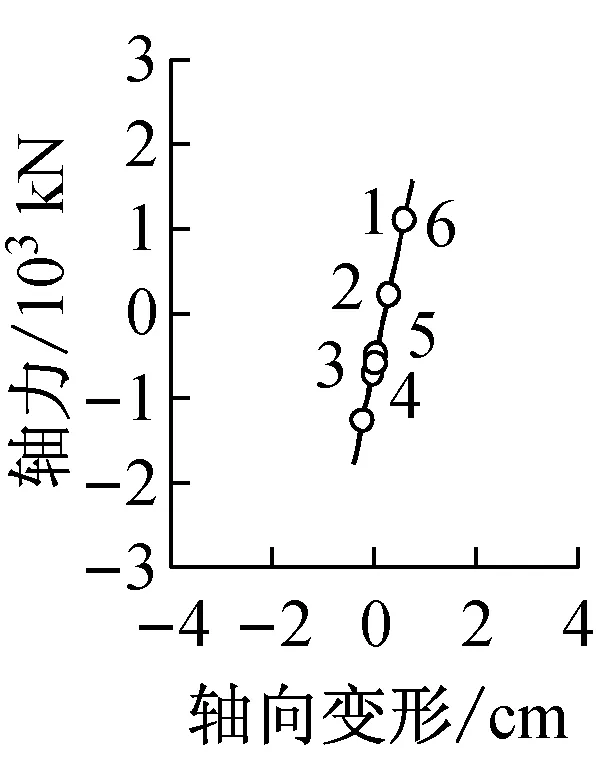
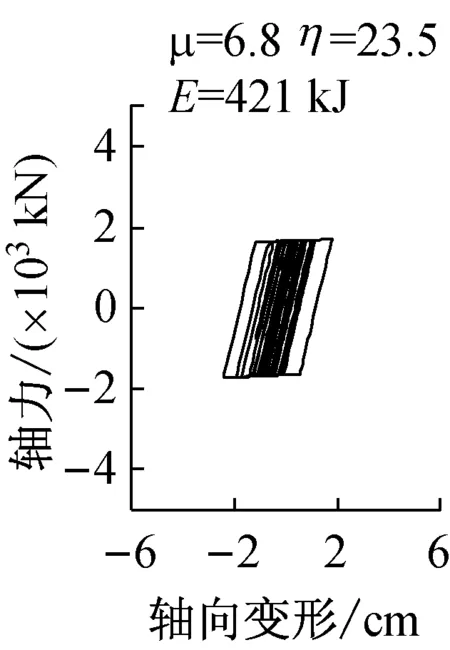
图7描述了在罕遇地震E3，T3以及特大地震K3作用下，各模型η值最大层BRB轴向力—轴向变形(N-δ)滞回曲线关系.图中：μ为延性比；η为累积塑性延性比；E为塑性吸收能量.

a RM33(BRB, E3)

b RM35(BRB, E3)

c RM63(BRB, T3)

d RM65(BRB, T3)

e PM93(BRB, K3)

f PM95(BRB, K3)

各模型β值越小，BRB屈服强度值越低，地震作用下BRB的累积塑性延性比η值越大，对BRB的需求性能要求越高，但BRB吸收的塑性能量却降低.各模型中，CB≈0.5的模型的BRB延性比μ以及累积塑性延性比η值并不全部小于CB≈0.3的模型，BRBF结构首层剪重比CB值从0.3增加到0.5，不一定能够减轻BRB的损伤；但是BRB吸收的塑性能量却有所增加.因此，实际建筑工程中使用的BRB持有性能必须大于BRB在强震作用下的需求性能.

3结论

采用两种多层BRBF典型结构形式模型为研究对象，以各模型的BRB水平力分担率平均值β和首层剪重比CB为主要研究参数，对研究模型进行弹塑性动力二阶非线性分析，探讨了多层BRBF结构抗震性能，结果如下：

(1)各模型最大层间位移分布，设防烈度地震作用下，各层分布较均匀；罕遇地震和特大地震作用下，RM模型首层和顶层以外的各层集中，PM模型因柱脚铰接致首层特别大，另外受第二振型影响第5和第6层也较大.

(2)强震作用下，BRBF结构中BRB吸收大量的塑性能量，BRB的减震效果明显；而BRBF结构首层剪重比CB从0.3增加到0.5时，不一定能够减少BRBF结构的层间位移和BRB的最大变形，结构基本周期和地震波卓越周期的影响更为明显；但CB从0.3增加到0.5时，能够减少BRB的累积变形.

(3)强震作用下，BRB水平力分担率平均值β≈30%的BRBF结构整体变形以剪切变形为主，第一振型卓越；β≈60%时，第二振型参与；β≈90%，第二振型卓越.

(4)强震作用下，在模型结构基本周期一定时，多层BRBF结构β值大小不影响地震输入总能量，各模型地震输入总能量大小主要取决于各模型基本周期；模型基本周期相近时，等效速度VE值基本相等；VE值从结构弹性基本周期以及地震波弹性体系能量谱可以推算得到，再次证明了基于能量平衡的抗震设计法的有效性.

(5)β值大小影响BRB需求性能；模型RM33的BRB的最大累积塑性延性比η达到80，而模型PM93的BRB的最大累积塑性延性比η为23.5；随着BRB水平力分担率平均值β值变小，对BRB需求性能要求提高.

参考文献:

[1]汪家铭, 中岛正爱, 陆烨. 屈曲约束支撑体系的应用与研究进展(Ⅰ) [J]. 建筑钢结构进展, 2005(1):4.

Wang J M, Nakashima M S, Lu Y. The practice and research development of buckling -restrained braced frames(I) [J]. Progress in Steal Building Structures, 2005(1):4.

[2]日本隔震结构协会.被动减震结构设计·施工手册[M].北京:中国建筑工业出版社，2008.

Japan Association of Isolated Structure. Passive damping design·Construction manual[M]. Beijing: China Architecture & Building Press, 2008.

[3]贾明明, 张素梅, 吕大刚, 等. 抑制屈曲支撑布置原则对钢框架抗震性能的影响 [J]. 工程力学, 2009 (7):140.

JIA Mingming, ZHANG Sumei, LÜ Dagang,etal. Influence of layout principle of buckling-restrained braces on aseismic performance of steel frame [J] .Engineering Mechanics, 2009 (7):140.

[4]叶列平, 程光煜, 曲哲, 等. 基于能量抗震设计方法研究及其在钢支撑框架结构中的应用 [J]. 建筑结构学报, 2012(11):36.

YE Lieping, CHENG Guangyu, QU Zhe,etal. Study on energy-based seismic design method and application on steel braced frame structures [J]. Journal of Bulding Structures, 2012(11):36.

[5]Choi H, Kim J, Chung L. Seismic design of buckling restrained braced frames based on a modified energy-balance concept [J]. Canadian Journal of Civil Engineering，2006, 33(2):1251.

[6]Choi H, Kim J. Energy-based seismic design of buckling restrained braced frame using hyteretic energy spectrum [J]. Engineering Structures，2006, 28(2):304.

[7]包恩和, 陈宜虎. 多层屈曲约束支撑钢框架抗震性能研究[J]. 结构工程师, 2013, 29(6): 98.

BAO Enhe, CHEN Yihu. The seismic response research of multi-layer buckling restrained braced steel frame [J]. Structural Engineers，2013, 29(6):98.

[8]包恩和,虞爱平,刘宝臣,等.多层屈曲约束斜撑钢框架弹塑性分析研究[J].四川建筑科学研究,2011(4):13.

BAO Enhe, YU Aiping, LIU Baocheng,etal．Plastic analysis on buckling restrained braced steel frame[J]．Sichuan Building Science，2011,37(4)：13.

[9]曾榕, 包恩和, 尹霞.多层屈曲约束斜撑钢框架静动力抗震设计 [J].广西大学学报: 自然科学版, 2012,37(4):690.

ZENG Rong, BAO Enhe, YIN Xia. Static and dynamic seismic design of multi-layer buckling restrained braced frame[J].Journal of Guangxi University: Natural Science，2012,37(4):690.

[10]秋山宏． 基于能量平衡的建筑结构抗震设计[M]．叶列平，裴星洙，译． 北京: 清华大学出版社，2010．

Akiyama H． Earthquake resistant design method for buildings based on energy balance[M]．Translated by YE Lieping， PEI Xingzhu． Beijing: Tsinghua University Press， 2010.

[11]Ogawa K，Tada M. Combined non-linear analysis for plane frame (“clap”) [C]//Architectural Institute of Japan Proceedings of 17th Symposium on Computer Technology on Information Systems and Applications. Tokyo：Showa Intelligence Press，1994：79-84.

[12]Housner G W. Limit design of structures to resist earthquakes[C/CD]∥Proceedings of the 1st World Conference on Earthquake Engineering. [S.l.]: WCEE, 1956.

[13]Housner G W. Behavior of structures during earthquakes[C/CD]∥American Society of Civil Engineers. [S. l.]: ASCE, 1956.

Seismic Research on Multi-story Buckling Restrained Braced Steel Frame

CHEN Yihu1,2,3, ZHAO Yanlin1, BAO Enhe2, ZHANG Min2

(1. College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China; 2. College of Civil Engineering and Architecture, Guilin University of Technology, Guilin 541004, China; 3. Bowen College of Management, Guilin University of Technology, Guilin 541006, China)

Abstract：To study the elastic-plastic dynamic performance of multi-story buckling-restrained braced steel frame (BRBF) which modeled separately with rigid and pinned models, the buckling-restrained brace (BRB) average horizontal force sharing ratio β and shear-weight ratio CB were used as the main parameters, and the second-order nonlinear elastic-plastic dynamic analysis method was adopted. The research results are as follows: Maximum story drift distributes more evenly under the seismic fortification intensity, concentrates except for the first and top floor in the great or rare earthquake with the rigid model, focuses on the first floor particularly with the hinged column base from the pinned model, and additionally focuses on middle and upper layers affected by the second vibration mode. When β ≈30% under the great earthquake, the shear deformation dominates the structure and the first vibration mode is excellent; β≈60%, the second vibration mode participates in; β≈90%, the second vibration mode is remarkable. β value does not affect the seismic input energy when the fundamental period is set down, and the equivalent velocity VE is basically the same during the similar fundamental period; Meanwhile, VE values can be derived from elastic fundamental period and seismic wave energy spectra, which once again shows the effectiveness of seismic design based on energy balance method.

Key words：buckling restrained brace (BRB) average horizontal force sharing ratio； higher vibration mode； member performance requirement； seismic design based on energy balance method

文献标志码：A

中图分类号：TU973.13; TU973.31

通讯作者：包恩和(1975—)，男，副教授，工学博士，主要研究方向为钢结构抗震、减震优化设计及高阶分析.E-mail:bao_enhe@126.com

基金项目：国家自然科学基金(51368013，51568016); 广西自然科学回国基金(2011GXNSFC018004); 广西高等学校科学研究项目(KY2015YB505)；广西高等学校特色专业及课程一体化建设项目(GXTSZY232)

收稿日期：2015—05—21

第一作者： 陈宜虎(1979—)，男，副教授，博士生，主要研究方向为钢结构抗震、减震优化设计及高阶分析.E-mail:cherif2009@gmail.com