PSWF调制信号功率谱旁瓣抑制方法

张　丹，郭　珈，王红萍

(中国人民解放军91550部队，辽宁 大连　116023)



PSWF调制信号功率谱旁瓣抑制方法

张丹，郭珈，王红萍

(中国人民解放军91550部队，辽宁 大连116023)

摘要：多路PSWF时域正交调制信号功率谱主瓣扩展和旁瓣较高，严重影响了系统的功率利用率和频谱效率。针对这一问题，从带通滤波器的窗函数设计入手，提出了一种正交PSWF调制信号的带通滤波器设计方案，有效抑制了功率谱的旁瓣功率，提高了调制信号的带内能量聚集性。理论和仿真结果验证了该方法的有效性。

关键词：椭圆球面波函数；功率谱；带通滤波器；Kaiser窗

椭圆球面波函数(Prolate Spheroidal Wave Function，PSWF)是频域带限且时域能量聚集性最佳的信号形式[1]，目前在超宽带[2-4]、卫星通信导航[5-6]、非正弦时域正交调制[7-9]等应用领域已有相关研究。在信号处理方面，利用PSWF构成的完备正交系表示其他时限或带限函数时，其精度要高于用sinc函数来表示[1,10]，因而该函数在超宽带信道估计[11]、射频识别信号检测[12]中也有相关研究。基于PSWF的时域正交调制系统虽然可以迅速提高系统的性能，但随着脉冲数的增大，会造成功率谱的主瓣扩展和旁瓣较高，影响系统的功率利用率和频带利用率。针对这一问题，从带通滤波器设计入手，对PSWF调制信号的功率谱旁瓣抑制方法进行了研究，提出了一种正交PSWF调制信号的带通滤波器设计方案，有效抑制了功率谱的旁瓣功率，增强了调制信号的带内能量聚集性。

1基于Kaiser窗函数的数字带通滤波器设计

数字滤波器传输函数的设计方法分为IIR滤波器设计方法和FIR滤波器设计方法两大类。IIR滤波器设计方法是利用模拟滤波器成熟的理论及设计图表进行设计的，所用的存储单元少，所以经济而效率高。但是IIR设计中只考虑了幅度特性，没有考虑相位特性，所设计的滤波器相位特性一般是非线性的，且相位的非线性越严重，使得设计复杂度大大增加。FIR滤波器设计则一般没有封闭形式的设计公式，其传输函数H(z)是z-1的N-1次多项式，在z平面上有N-1个零点，原点z=0是其N-1阶固定重极点，通常只能用较多的阶数达到高的选择性。FIR滤波器在保证幅度特性满足技术要求的同时，能够保持线性相位，同时其传输函数的极点固定在原点又保证了系统的稳定性。基于上面的分析，采用FIR设计带通滤波器，并用于抑制调制信号功率谱的带外频率分量。

在FIR数字滤波器的窗函数中，Hamming窗函数的最大旁瓣值比Hanning窗低，但其主板宽度与Hanning窗相同；Blackman窗的最大旁瓣值最低，但其主板宽度最宽；而Kaiser窗是由零阶贝塞尔函数构成的，是一组可调的窗函数，可以通过调节参数n来控制窗函数的宽度，调节参数β来控制旁瓣的高度，在设计中可根据滤波器的衰减指标确定窗函数的形状。因此，选取Kaiser窗函数用于带通滤波器设计。

基于Kaiser窗的带通滤波器的设计参数主要有滤波器阶数n、滤波器系数β，采样频率Fs、通带下截止频率Fc1和上截止频率Fc2。在设计带宽B=250 Hz，频谱范围1 000～1 250 Hz，采样频率Fs=12 800的情况下，基于Kaiser窗的带通滤波器的具体参数设置如表1所示。

表1 时域正交PSWF脉冲组和Kaiser

按照表1的参数设置，设计的基于Kaiser窗的带通数字滤波器如图1所示。

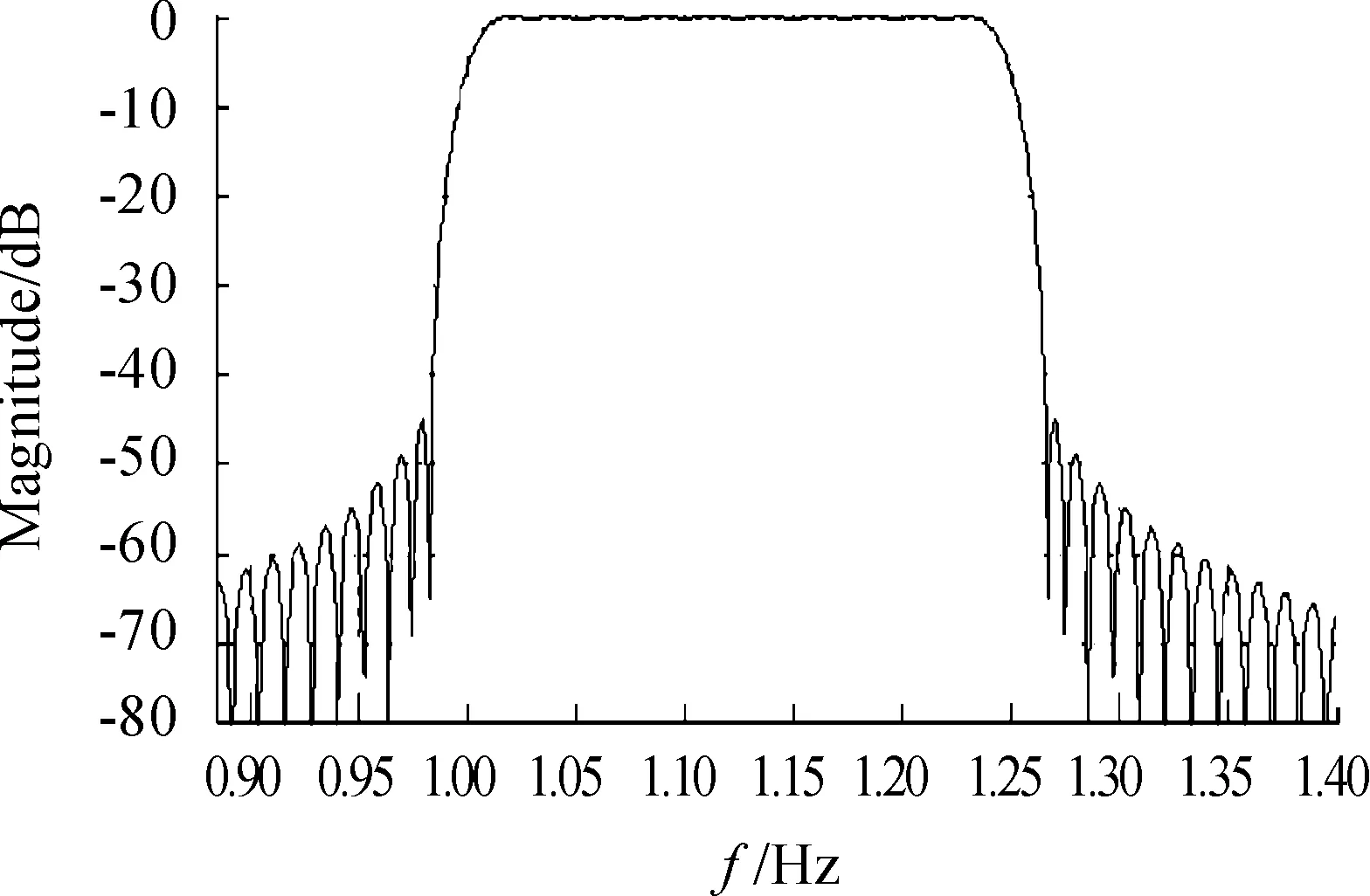
图1　基于Kaiser窗的带通数字滤波器

由图1可以看出，设计的带通滤波器在给定的频段范围内的幅度相对稳定，只是在接近上下截止频率处有所衰减。正是基于这样的特点，才在保持调制信号带内能量聚集性的同时，有效抑制了功率谱的旁瓣功率。

2带通滤波器对调制信号影响的理论分析

使用带通滤波器可以提高调制信号的功率谱截止带外衰减功率，但同时也必然引起一定程度的信号时延和波形失真，影响解调端正交脉冲调制信号与各路正交PSWF脉冲模板信号的相关输出判决量，进而影响正交脉冲调制系统的误码性能。通过理论推导分析了滤波过程对正交脉冲调制信号与各路正交PSWF脉冲模板信号的相关输出判决量的影响。

2.1FIR带通滤波器引起的信号时延特性分析

FIR滤波器在保证幅度特性满足技术要求的同时，很容易做到严格线性相位特性。而线性相位特性对于系统无畸变传输具有重要的意义。只有输出信号是由输入信号经过一致的放大/衰减或延迟产生时，系统才能无畸变地传输信号。无畸变传输系统在离散时间域和z变换域可以分别描述为：

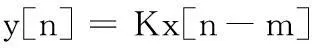
(3)

(4)

其中:K为恒定实数;m为正整数。

由此可以得到无畸变传输系统在频域和z变换域的系统传递函数分别表示为：

(5)

(6)

其中:对于任意角频率ω，传递函数的幅度K(jω)≡K，K(z)=K；传递函数的相位θ(ω)满足线性变化特性θ(ω)=-ωτ。

对于FIR带通滤波器，其系统传递函数H(jω)的幅值K(jω) 不可能为恒定的实数，因此无法严格做到完全无失真的传输，但是可以实现严格的线性相位。为了实现严格的线性相位特性，必须保证H(jω)的相位θ(ω)与幅度K(jω)无关，这就要求K(jω)可以不是恒定的实数，但必须是实数，即满足共轭对称特性，K(jω)=K(-jω)。由此得到数字带通滤波器具有线性相位的条件为

(7)

对应的z变换域表示为

(8)

其中:K(z)为幅值传输函数; m为FIR数字带通滤波器的固定离散时间延迟。对于滤波器长度为N，冲击响应为h(n)的FIR滤波器，若满足条件 h(i+(N-1)/2)=h(-i+(N-1)/2)，则

(9)

滤波器传输函数满足线性相位条件，由式(9)可知，此时FIR带通滤波器的固定离散时间延迟为(N-1)/2。

由以上分析可知，当N为偶数时，FIR滤波器在冲击响应函数 h(n) 满足条件 h(i+N/2-1)=h(-i+N/2)时，具有线性相位特性，其固定离散时间延迟为N/2；当N为奇数时，FIR滤波器在冲击响应函数h(n)满足条件 h(i+(N-1)/2)=h(-i+(N-1)/2)时，具有线性相位特性，其固定离散时间延迟为(N-1)/2。

2.2FIR滤波器对信号时域波形的影响

为了便于分析，以两路正交PSWF脉冲调制信号为例进行分析。令φ1(t)和φ2(t)，0≤t≤T，分别表示相互正交的两路PSWF脉冲信号，它们的M点离散采样信号分别为φ1(n) 和φ2(n)，n=1,2,…,M。则连续K个码元时间的两路正交PSWF脉冲调制系统总的调制信号表示为

(10)

各路调制信号分别表示为

(11)

(12)

假设系统采用FIR数字滤波器为长度N(为偶数)，其冲击响应函数为h(n),n=0,1,…，N-1，则调制信号s(n)滤波后得到的时域信号为

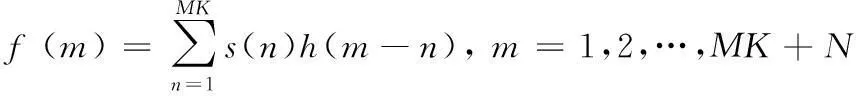
(13)

此时，根据FIR滤波器的时延特性可知，滤波后的调制信号s′(n)为

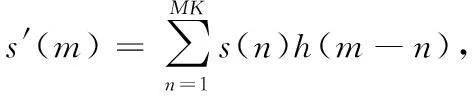
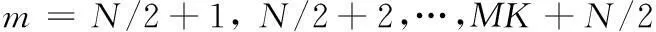
(14)

且由滤波器冲击响应函数的性质可知，当(m-n)<0或(m-n)≥N时，h(m-n)=0，故滤波后的调制信号s′(m)又可以具体表示为

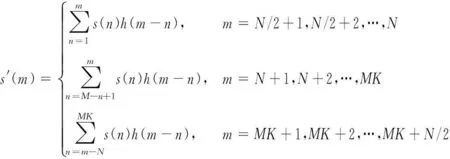
(15)

由式(15)可知，滤波后调制信号s′(m)在m时刻的取值与调制信号在n=m时刻之前最多N个采样值有关，由它们根据滤波器冲击响应函数h(n)加权叠加得到。因此，滤波器的长度N越大，原调制信号s(n)中每个采样值s(n)影响的滤波后调制信号s′(m)的采样点数越多，滤波计算越复杂。

3性能分析及数值仿真

为了验证和比较该脉冲设计方法的性能，下面从设计脉冲的正交性、算法时间复杂度和空间复杂度3个方面对该正交脉冲设计方法进行仿真分析。

3.1带通滤波器对调制信号时延和时域波形的影响

时间同步直接影响接收信号与正交脉冲模板信号间相关特性，也是进一步影响正交脉冲调制解调性能的关键因素之一，而通过上一节的理论分析可知，滤波处理过程必然带来一定的信号延迟，因此确定滤波过程引起的信号时延对于进一步分析带通滤波对脉冲相关特性和正交脉冲调制解调性能的影响具有重要的意义。上一节对带通滤波过程引起的信号时延特性进行了理论分析，为了验证该理论分析的正确性，并为进一步对滤波器影响分析打下基础，本节将通过仿真定量分析滤波过程引起的信号时延特性，以及滤波对脉冲相关特性和系统误码性能的影响。

本节仿真采用与第1节仿真条件相同的基本参数设置：设计带宽B=250 Hz，频谱范围为1 000～1 250 Hz，码元时间宽度Ts=40 ms，总时间带宽积为C=BT=10，子频带划分数k=4，频谱交叠度ρ=50%。

按以上参数设置条件得到的由16个PSWF脉冲经过时域正交调制后的调制信号的时域波形图和归一化功率谱特性图如图2所示。

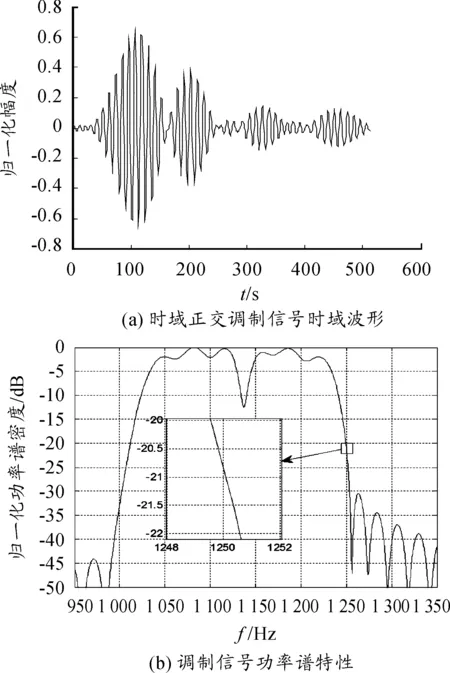
图2　时域正交调制信号的时域波形图和归一化功率谱

首先验证2.1节的带通滤波器对信号时延的影响。基于Kaiser窗的带通滤波器参数设置为：滤波器阶数N=1 024，滤波器系数β=4，下截止频率为Fc1，上截止频率为Fc2。

按照所得滤波器冲击响应序列h1(n)，利用Matlab自带的filter函数可以方便地实现信号的时域滤波。其实具体操作过程是将输入序列s(n)与长度为N的滤波器冲击响应序列h1(n)做卷积后，舍弃最后N个值，得到与输入序列s(n)等长度的输出序列s′(n)。当输入信号s(n)为如图3(a)所示10个码元时间的1阶PSWF脉冲调制信号时，经过h1(n)滤波后的输出信号s′(n)如图3(b)所示。为了便于比较，对调制幅度进行了归一化处理。

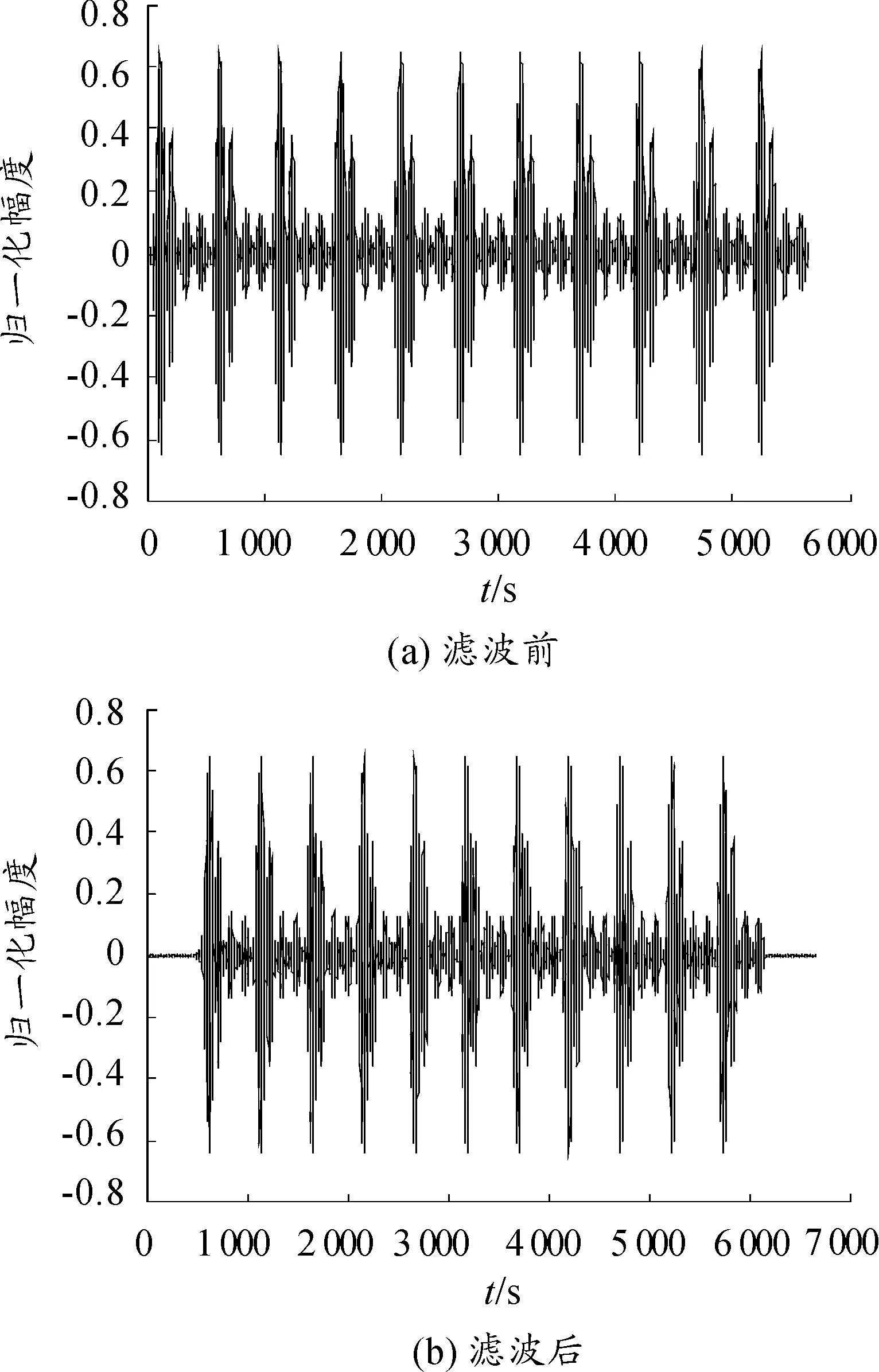
图3　滤波前后11个码元的时域波形

根据2.1节的理论分析可知，在滤波器长度N为偶数1 024 时，滤波过程的理论延迟为N/2=512个采样时间，恰为一个码元周期。由图3可见，输出信号s′(n)的相位和幅度与输入信号s(n)基本保持一致，但从细节上看，滤波延时后输出信号s′(n)与输入信号s(n)在相位上仍存在差别，这种差别在两码元相接处较明显，即滤波后在码元相接处存在相位失真和幅度失真，但这种失真是带通滤波器都存在的问题，在此不作深入讨论。

因此，采用上述基于Kaiser窗的带通滤波器仅在两码元的相接处会引起调制脉冲信号的失真，基本不影响调制信号的功率谱特性，且带通滤波器引起的信号时延与理论分析基本一致。

3.2带通滤波器对调制信号功率谱特性的影响

通过前面的分析可知，可以从系统设计层面，通过设计带通滤波器的方式，增加带通滤波模块来抑制带外频率分量，提高调制信号带外衰减。为了定量分析带通滤波器对调制信号的功率谱特性能的改善程度，下面对滤波前后调制信号的功率谱进行了仿真。

为了方便比较滤波前后调制信号的功率谱特性，依然与第1节的仿真条件相同的基本参数设置：设计带宽B=250 Hz，频谱范围为1 000～1 250 Hz，码元时间宽度Ts=40 ms，总时间带宽积为C=BT=10，子频带划分数k=4，频谱交叠度ρ=50%。并按照表1的参数设置来设计带通滤波器：下截止频率Fc1=1 000 Hz，上截止频率Fc2=1 250 Hz，滤波器阶数N=1 024，滤波器系数β=4。按照上述参数设置，对滤波前后调制信号的归一化功率谱进行了仿真，结果如图4所示。

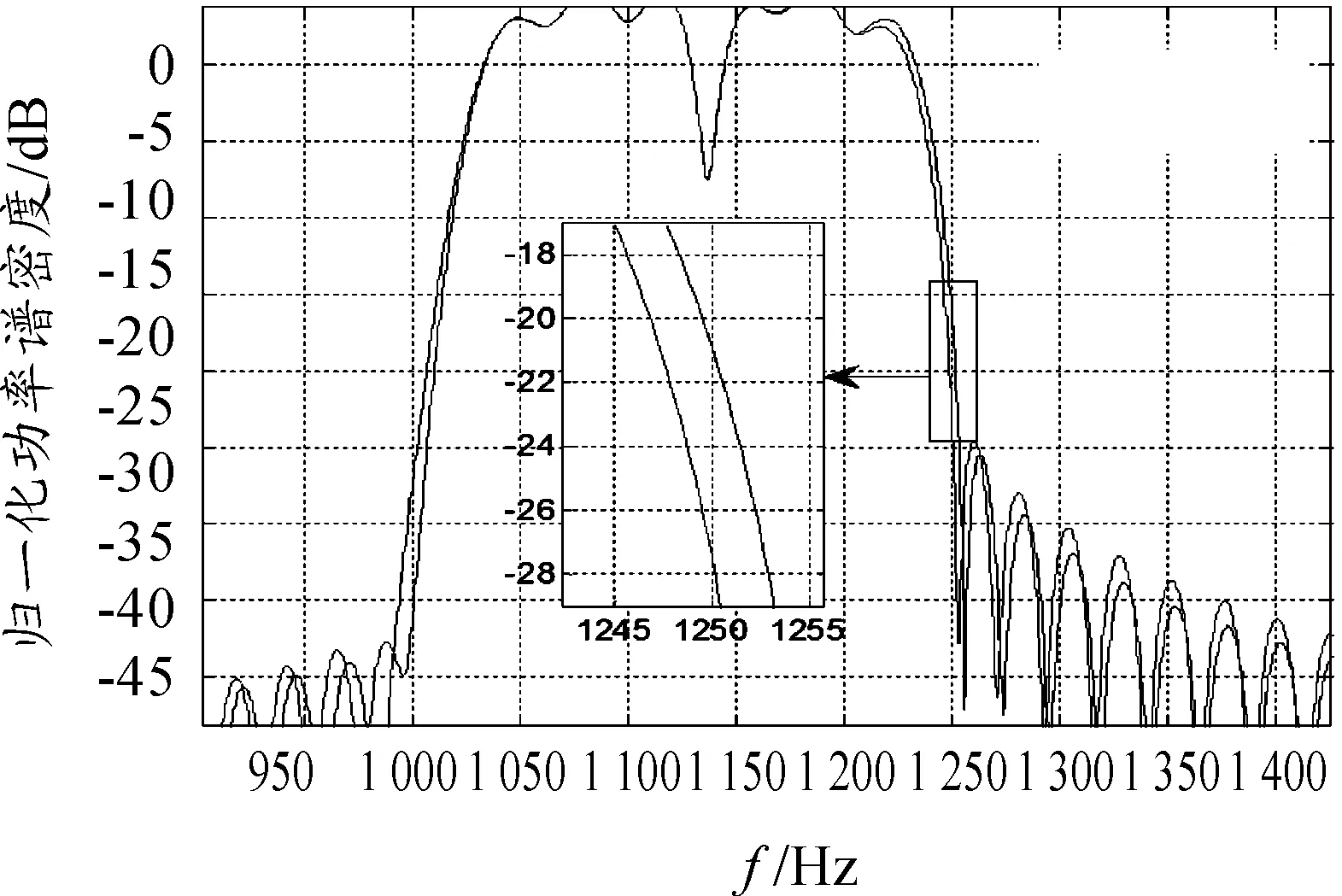
图4　滤波前后调制信号的功率谱特性

从图4可以看出，滤波前后调制信号的归一化功率谱在给定的频段范围内变化不大，仅在接近截止频点处以外的频段变化明显，这和设计的带通滤波器的幅频特性有关。从图4明显可以看出，在上截止频点1 250 Hz处调制信号功率谱带外衰减，由滤波前的-21 dB提高到滤波后的-27 dB，在下截止频点1 000 Hz处调制信号功率谱带外衰减，由滤波前的-33 dB减少到滤波后的-41 dB，可见所设计滤波器能够达到带外频率分量抑制的效果，且功率谱特性改善较为明显。

4结束语

针对时域正交调制信号的功率谱主瓣扩展和旁瓣升高，通过对窗函数的研究分析，设计出一种方便可调的带通滤波器，并在基于PSWF的调制解调系统中增加带通滤波模块，抑制调制信号的截止带外衰减功率；分析了带通滤波器对调制信号特性和系统解调性能的影响，并通过数值仿真对本文方法的带通滤波前后调制信号的PSD及波形仿真，验证了本文方法的有效性。

参考文献：

[1]SLEPIAN D，POLLAK H O.Prolate spheroidal wave functions,Fourier analysis,and uncertainty-I[J].Bell Syst Tech J,1961,40(1):43-46.

[2]PARR B,CHO B,WALLACE K.A novel ultra-wideband pulse design algorithm[J].IEEE Communication Letters,2003,7(5):219-221.

[3]陆音，朱洪波.基于近似扁长椭球波函数的超宽带脉冲设计[J].通信学报，2005，26(10):60-64.

[4]马英杰，周正，何文才，等.认知UWB正交脉冲序列设计及性能分析[J].北京理工大学学报，2011,5(31):583-588.

[5]LAUDIO C S,ROSSI T,MARINA R.Efficient Waveform Design for High-Bit-Rate W-band Satellite Transmissions[J].IEEE Transactions on Aerospace and Electronic Systems,2011,47(2):974-995.

[6]周艳玲，胡修林，唐祖平.长椭圆球波函数在卫星导航中的应用研究[J].宇航学报,2011,32(9):1890-1894.

[7]张榛，王红星，张磊,等.一种改进的正交PSWF脉冲设计方法[J].中国电子科学研究院学报,2013,8(4):388-392.

[8]王红星，赵志勇，刘锡国,等.非正弦时域正交调制方法[P].中国：ZL200810159238.3,2009-04-15.

[9]陈昭男，王红星，钟佩琳,等.基于Givens旋转变换的PSWF调制脉冲信号PAPR抑制方法[J].电子与信息学报，2013，35(6):1406-1412.

[10]SLEPIAN D.Prolate spheroidal wave functions,Fourier analysis,and uncertainty-V:The discrete case[J].Bell System Tech Journal,1978,57(5):1371-1430.

[11]LAURENT GOSSE.Effective band-limited extrapolation relying on Slepian series and l1regularization[J].Computer and Mathematics with Applications,2010(60):1259-1279.

[12]WOUTER DULLAERT,LARS REICHARDT,HENDRIK ROGIER.Improved Detection Scheme for Chipless RFIDs Using Prolate Spheroidal Wave Function-Based Noise Filtering[J].IEEE Antennas and Wireless Propagation Letters,2011(10):472-475.

(责任编辑杨继森)

本文引用格式：张丹，郭珈，王红萍.PSWF调制信号功率谱旁瓣抑制方法[J].兵器装备工程学报，2016(4):128-131.

Citation format:ZHANG Dan, GUO Jia, WANG Hong-ping.Power Spectral Density Reduction Method Research for PSWF Modulated Signals[J].Journal of Ordnance Equipment Engineering,2016(4):128-131.

Power Spectral Density Reduction Method Research for PSWF Modulated Signals

ZHANG Dan, GUO Jia, WANG Hong-ping

(The No. 91550thTroop of PLA, Dalian 116023, China)

Abstract:Multiple PSWF modulated signals have spread PSD mainlobe and large sidelobe, which decreases power utilization and spectral efficiency of the communication system. Aimed at this problem, starting from the window function design of bandpass filter, a novel bandpass filter design scheme for modulated PSWF signals was proposed. The scheme effectively reduces the sidelobe power and increases the energy concentration of modulated singals. The theoretical and simulation results verify the effecicy of proposed method.

Key words:prolate spheroidal wave function; power spectrum; bandpass filter; Kaiser window

文章编号：1006-0707(2016)04-0128-05

中图分类号：TN911.7

文献标识码：A

doi:10.11809/scbgxb2016.04.031

作者简介：张丹(1983—),女,硕士研究生,助理工程师,主要从事通信与信息工程研究。

收稿日期：2015-10-29；修回日期：2015-11-26

【信息科学与控制工程】