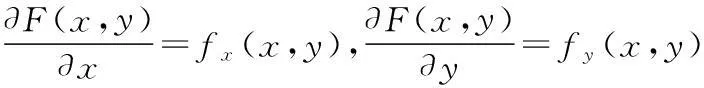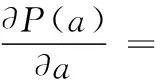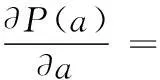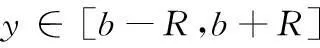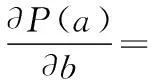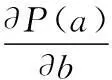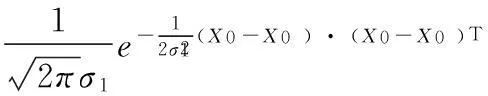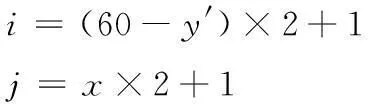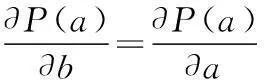有限探测区域最大概率探测点寻优算法

张　驰,陈建勇

(海军航空工程学院 电子信息工程系,山东 烟台　264001)



有限探测区域最大概率探测点寻优算法

张驰,陈建勇

(海军航空工程学院 电子信息工程系,山东 烟台264001)

摘要：研究了二维空间有限区域目标探测的最大概率探测点的计算问题。任意分布密度条件下目标的空间发现概率是空间面积上的积分,推导了发现概率对探测点梯度的一元积分的表达式，用于最大发现概率探测点的寻优计算，能够缩短计算时间，提高计算精度。

关键词：最优搜索；梯度；直升机；吊放声纳

在一般的最优搜索理论研究中，对于连续空间中的连续运动目标，往往考虑的是连续空间的连续探测路径[1-2]；对于离散空间中的目标，其离散空间单元是确定的单元[3]。在离散确定的单元中，找到目标概率分布最大的点进行探测能够提高搜索效率。直升机吊放声呐搜潜是一种在连续空间对不确定的离散区域在离散时刻进行搜索的问题[4]。吊放声呐的探测范围一般是圆形探测域。直升机吊放声纳按照时间顺序进行多点探测目标的计算，涉及到任意目标分布密度下局部最大探测点的寻优计算。传统的目标寻优方法是运用直接法，本研究提出了一种基于梯度的寻优算法，比传统的算法效率更高。依据建立起的单点探测发现概率模型[4]，推导出了发现概率对探测点梯度的一元积分表达式，并用于寻优计算中。

传统的直接法在二维空间中进行目标的局部探测搜索，是将该区域中划分的单元格中进行依次的概率求解，比较该区域概率最大点。存在着一定的缺陷与不足，其搜索时间将会受到区域大小，划分精度的影响，若区域范围较大或者划分精度高则会使计算效率变小。采用梯度算法将会避开对区域中所有的单元格进行求解，且初始探测点的位置可以随机选取，在最大发现概率的数值寻优计算中将会提高解算效率，梯度向量的计算也将在多点探测以及全局探测中起到非常重要的作用[5-7]。

1梯度寻优算法基本模型

1.1参数定义和概率模型

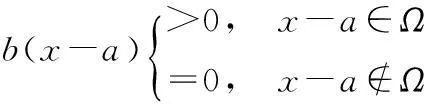
(1)

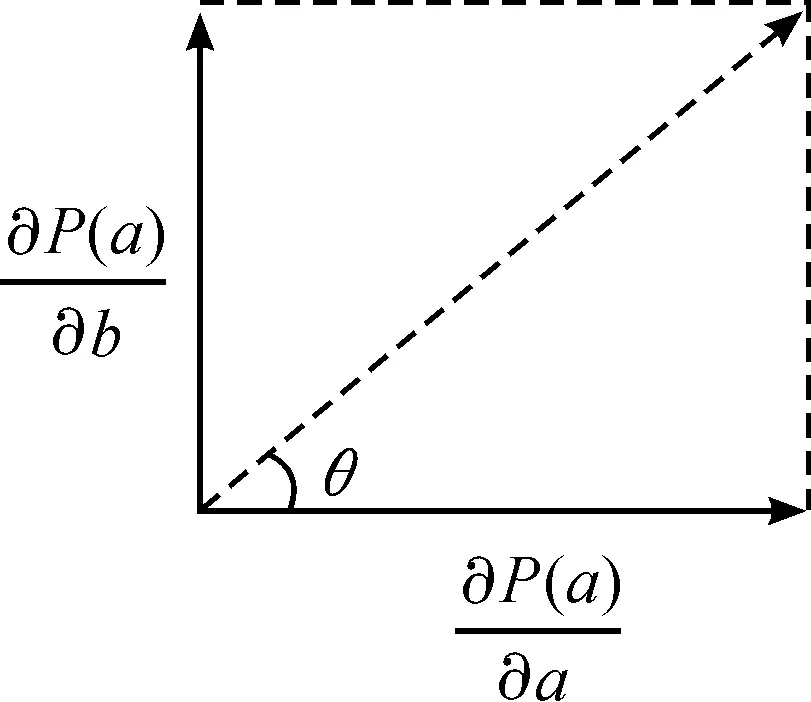
发现概率对探测点a的梯度为

(2)

1.2基于梯度寻优算法计算

得到梯度的计算式后，接下来将求解梯度分量的计算方法。将探测点周围的探测范围设为凸集Ω。假设凸集Ω的非0边界曲线y=φ1(x)和y=φ2(x)是连续封闭可导的。假设φ1(x)>φ2(x)，x∈[mx,Mx]；φ1(mx)=φ2(mx)，φ1(Mx)=φ2(Mx)。

同样有Ω的非0边界曲线x=h1(y),x=h2(y)是连续封闭可导的。假设h1(y)>h2(y)，y∈[my,My]；k1(my)=k2(my)，h1(My)=h2(My)。

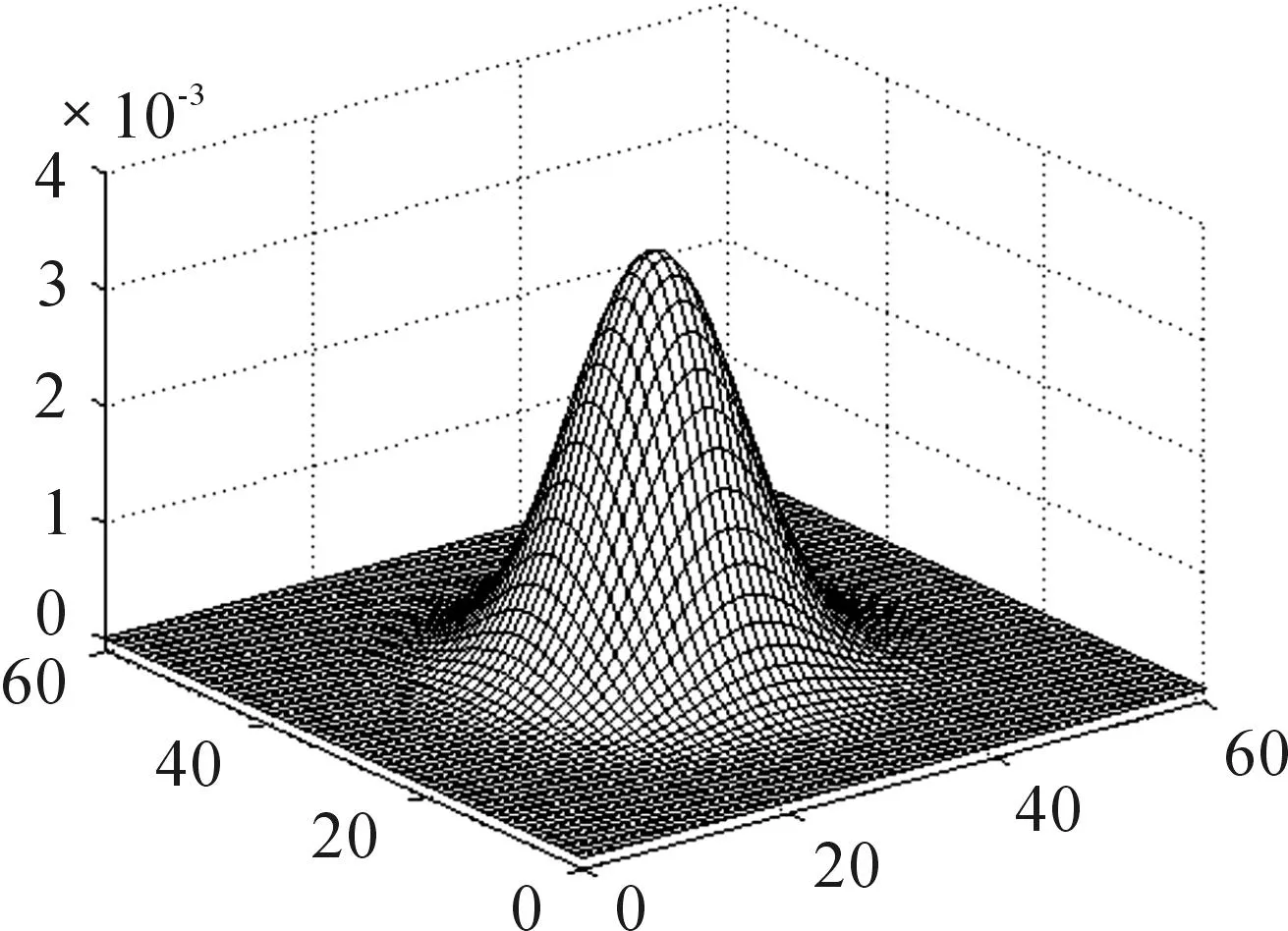
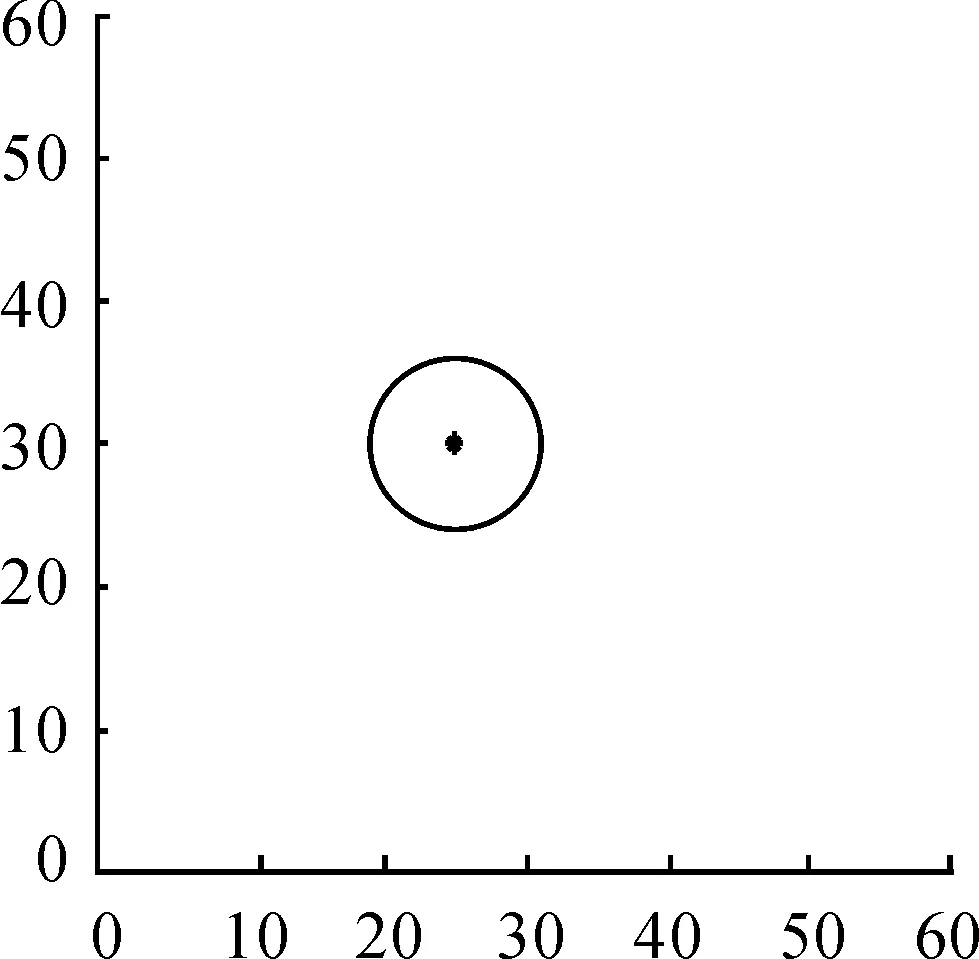
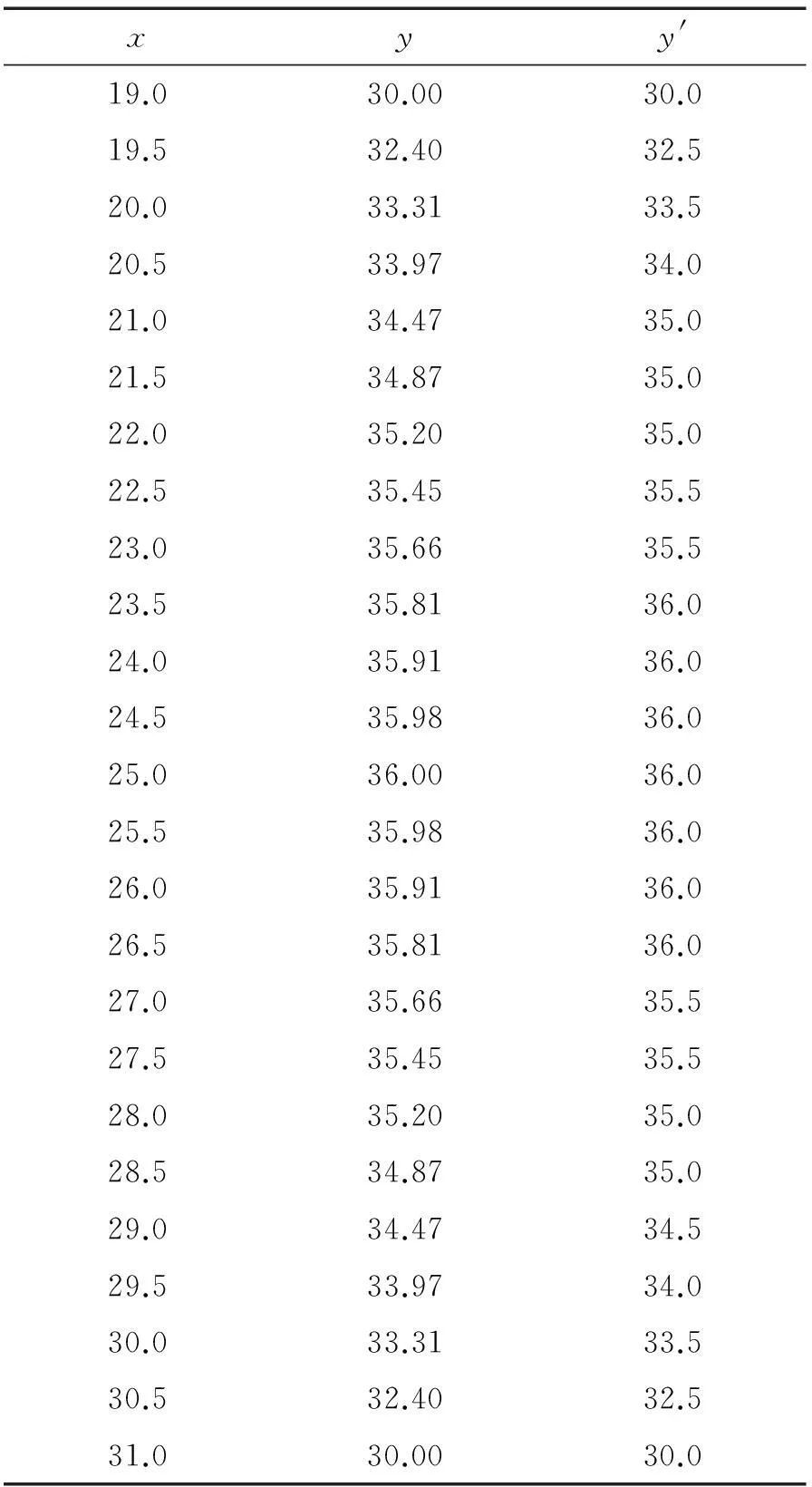
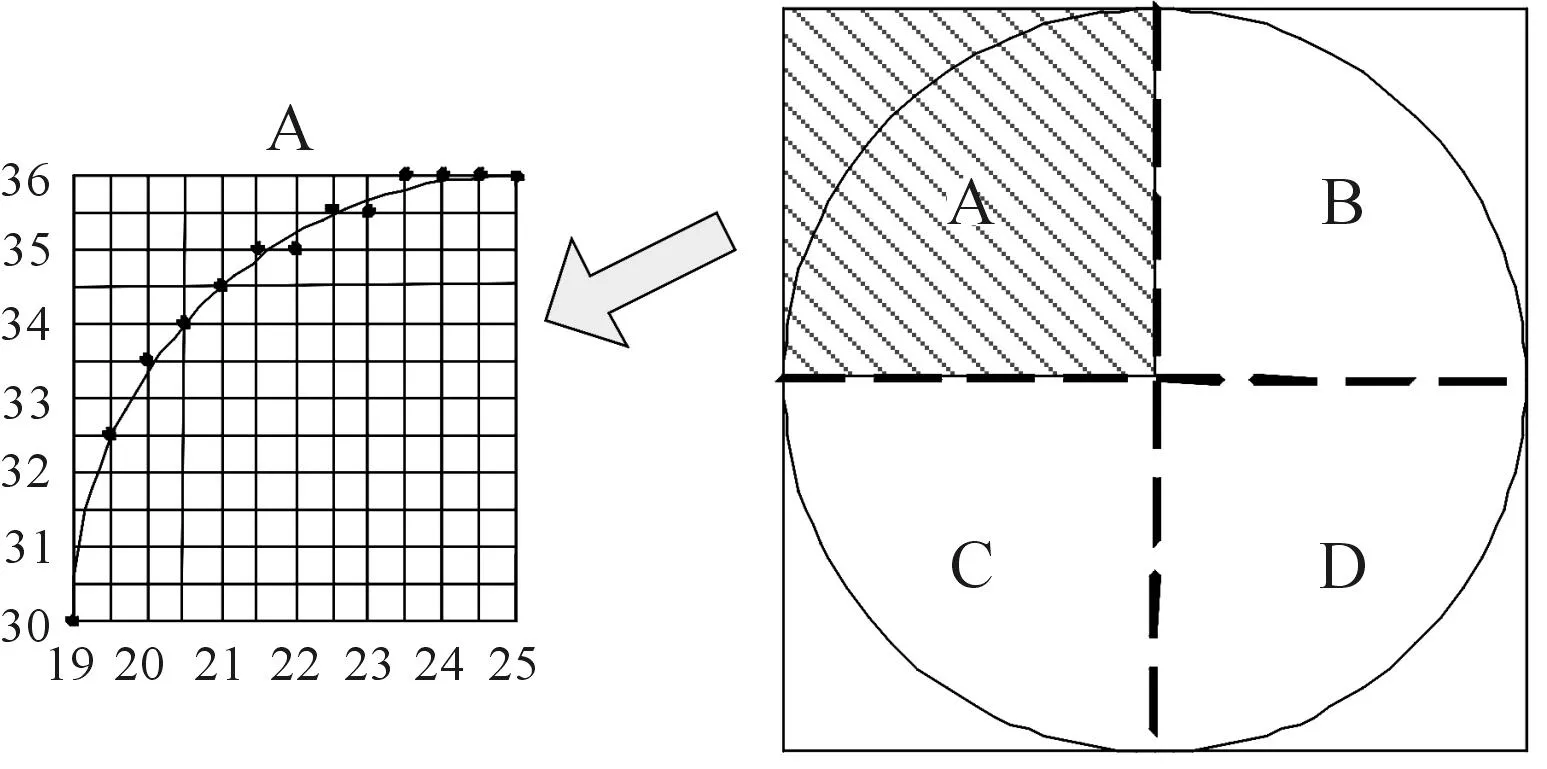
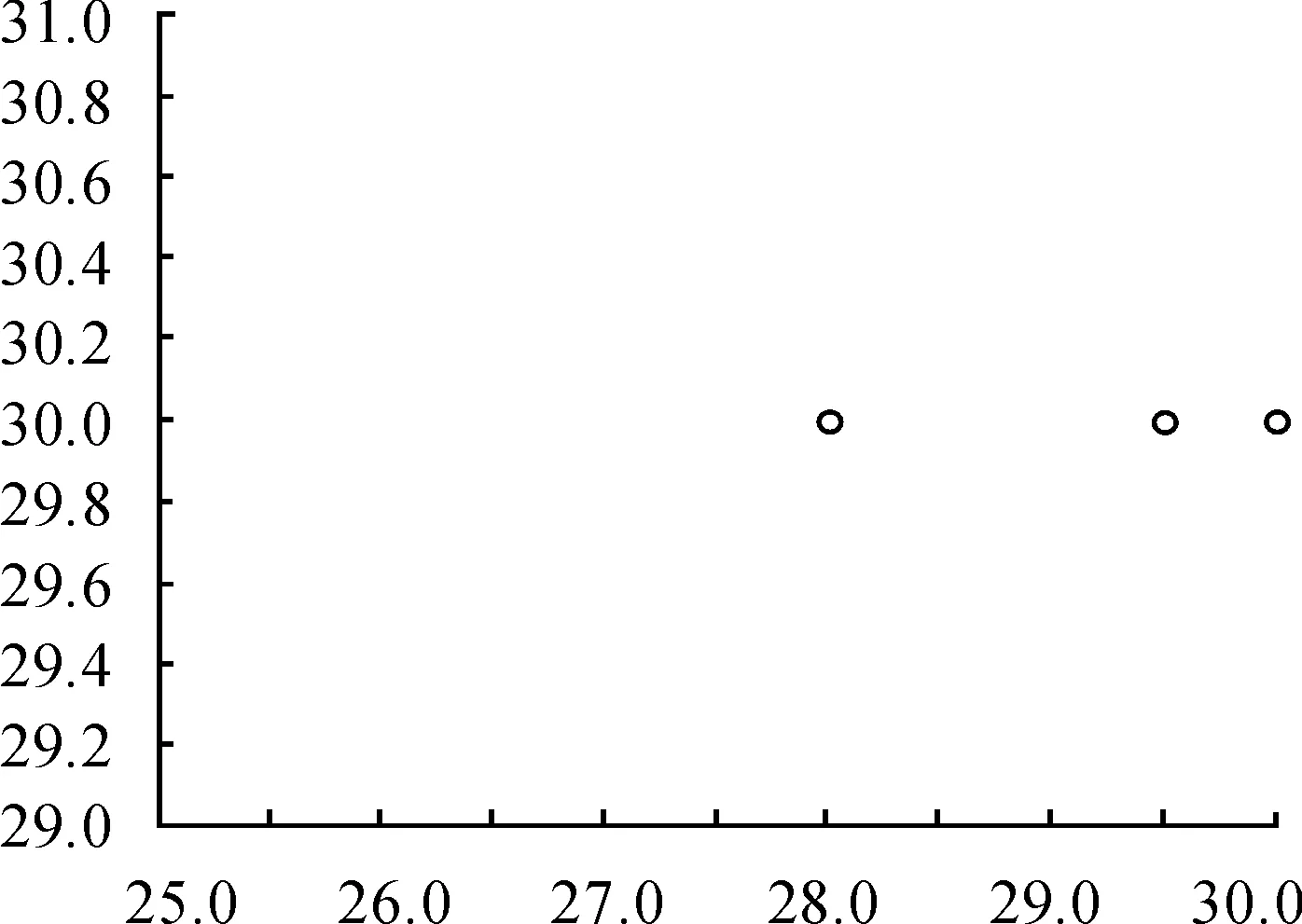
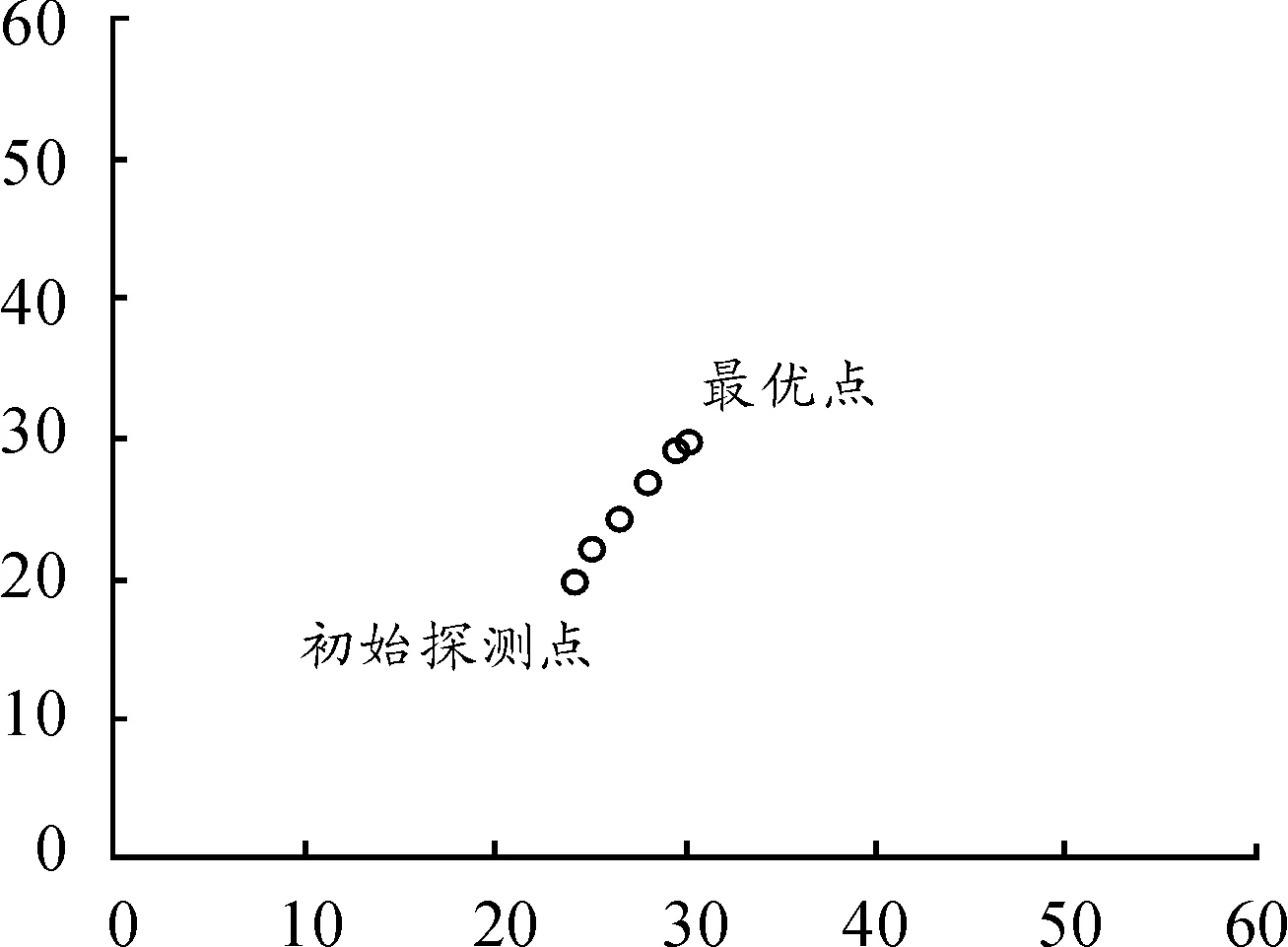
定义(ξ,η)为发现目标时目标所处的位置，定义概率函数F(x,y)=P{ξ

P(a) = ∬Ωb(x-a,y-b)ρ(x,y)dxdy=

(3)

令fx[x,φ1(x)]关于x的原函数为F1(x,a,b)，fx[x,φ2(x)]关于x的原函数为F2(x,a,b)，则：

(4)

因为a∈Ω，所以有常数rx>0,Rx>0，ry>0,Ry>0使：

a-rx=mx,a+Rx=Mx，b-ry=my,b+Ry=My。则有：

(5)

P(a)对a的偏导数可以表示为：

fx[Mx,φ1(Mx)]-fx[mx,φ1(mx)] +

{fx[Mx,φ2(Mx)]-fx[mx,φ2(mx)] +

变换其中的微分变量，得到：

(6)

同理

(7)

当a为局部最大点时，有▽aP(a)=0，即：

(8)

2算例仿真

由于吊放声呐的探测范围一般为圆形区域[8]，所以设探测域Ω是半径为R的圆型域。令a表示Ω的圆心，同时也是探测点的位置。

对于半径为R的圆域边界曲线，Ω边界的上半圆、下半圆和左半圆、右半圆可以用圆心和半径表示为：

由式(6)、式(7)可得到圆形区域下的具体表达式

(9)

(10)

式(9)中：第一项为探测函数与分布密度的乘积在Ω右边界上的积分；第二项为在Ω左边界上的积分。式(10)中：第一项为探测函数与分布密度的乘积在Ω上边界上的积分；第二项为在Ω下边界上的积分。

陈律师沉思着答道：“刚得到她过世的消息，我很震惊，因为几天前她刚叫我去修改了遗嘱，那时候她还好好的，这实在是很蹊跷。但她是因为和她侄子发生争执过于激动引发心脏病而死，是正常死亡，我就想不出这还有什么解释了，只能说是那个保姆命太好了。”

图1　下一点前进的方向

最优计算的具体步骤：

第1步，确定探测精度和相关参数

将60×60的海域按照精度0.5 n mile的间隔划分成单位点。

对区域内的某一点进行探测，根据初始目标分布和初始速度分布，可以得到初始时刻的目标分布概率如图2所示。

图2　目标分布概率

第2步，以区域内任意一点作为起始探测点

该区域的目标分布中假设任找一点(25,30)作为起始探测点，如图3所示。

图3　随机选取的探测点

图3中红色边界即为距离探测圆心点为6 n mile的边界圆，下一步找到对应的点坐标。根据式(10)，以圆的左上半部分为例，将其划为A部分，如图4所示。x的取值从19到31，按照间隔0.5划分，能够求出对应的y点值。由于y方向的取值也是按照步长0.5 n mile划分，所以需将y的值进行近似，将y的值近似成0.5的倍数得到y′值。该部分各点的对应关系如表1所示。

表1　对应的坐标点

第4步，找到相关点所在区域数组中对应的目标概率密度值

图4　A部分对应的目标概率密度值

同理，可以得到其余B，C，D三部分的取值。分别得到4个区域中圆域边界上对应的位置坐标，得到坐标点后根据其在数组中寻址就能找到对应点处的目标概率密度值，对于按照第一部划分好的数组，将i,j分别表示行、列的索引，该数组寻址可以表示为A(i,j)。点坐标(x,y′)与数组的(i,j)存在以下对应关系：

例如，(x,y′)=(19,30)点出对应的行和列(i,j)=(61,39)，第61行39列中的概率分布值为ρ(61,39)=9.22×10-4。

第5步，对探测点处的梯度进行求解

(11)

(12)

将式(11)、式(12)分别进行数值积分然后求差值。式(9)同理可得。

式(10)中，当b(x-a,y-b)关于x=b对称，有：

当探测函数b(x-a,y-b)在Ω的边界上有b(x-a,y-b)≡Β，则：

(12)

若Β>0，则按照式(12)进行求解，当Β=0，令β=1，可得

(13)

同理，

(14)

量值在设β=1造成的差异，可以在梯度方向的步长上进行调整。

在点(25,30)处求出c1=0.052，c2=0.052，c3=0.026 6，c4=0.086 2，得到d1=0.059 6，d2=0(注意，这里d1的正负号代表左右方向上的移动，正号向右，负号向左；d2的正负号代表上下方向上的移动，正号向上，负号向下)，则下一点的方向向右移动，经计算，移动3次后到达最优点(30,30)。如图5所示，寻优点轨迹。

图5　起始点在(25,30)的寻优路线

此算例中，起始点寻找最优点只做了水平方向上的移动，现假设一个更具有一般性的点(24,20)，在其他初始条件不变的情况下求得寻优轨迹如图6所示，经过6步后找到最优探测点位置。

图6　起始点在(24,20)的寻优路线

经验证，点(30,30)确实为该区域分布函数中目标概率最大的点。

3结论

通过算例可以得出梯度寻优算法能够很快的找到区域内探测概率最大点，计算速度远快于传统的直接求解法。本文研究了在建立的有限区域探测的模型中，求离散点搜索探测概率最大点的寻优算法问题。将二维空间最大发现概率探测点的寻优问题，转化为发现概率对探测点的梯度计算问题，而该问题在二维空间是一个一元积分的表达式，可以较快地计算出概率梯度，进而使用最速下降法等方法，数值计算逼近最优探测点。

参考文献：

[1]肖斌，徐宏飞.搜索力最优配置的求解与收敛性分析[J].火力与指挥控制,1998,23(4):36-39.

[2]王景奇，范奎武，张最良.机动目标对搜索的最优规避[J].军事系统工程,2001,11(1):4-9.

[3]李长明，杨健.准最优增量搜索效率分析[J].火力与指挥控制,2000,25(4):49-51.

[4]陈建勇，王健，单志超.离散时间探测随机恒速目标的最优搜索算法[J].系统工程与电子技术，2013,35(8):1627-1630.

[5]解可新,韩健,林友联.最优化方法[M].天津:天津大学出版社,2004:94-96.

[6]MANGEL M.Search for a randomly moving object[J].SIAM Journal of Applied Mathematics,1981(40):327-338.

[7]吴沧浦，夏元清，杨毅.最优控制的理论与方法[M].北京：国防工业出版社,2013:147-161.

[8]陈建勇,冷江,于传健.使用吊放声纳的直升机应召搜潜发现概率[J].海军航空工程学院学报,2004,19(5):559-561.

(责任编辑周江川)

本文引用格式：张驰,陈建勇.有限探测区域最大概率探测点寻优算法[J].兵器装备工程学报，2016(4):118-122.

Citation format:ZHANG Chi,CHEN Jian-yong.Optimize Algorithm of the Maximum Probability of Detection Points in Limited Detection Area[J].Journal of Ordnance Equipment Engineering,2016(4):118-122.

Optimize Algorithm of the Maximum Probability of Detection Points in Limited Detection Area

ZHANG Chi, CHEN Jian-yong

(Department of Electronic and Information Engineering, Naval Aeronautical and Astronautical University, Yantai 264001, China)

Abstract:This dissertation researched calculation problem about the maximum probability of detection points of limited detection area in a two dimensional space. Under the condition of arbitrary distribution density, the discovering probability in space equals to integral on the space area. This thesis deduced one dimension integral expression of discovering probability to detection point of the gradient, which was used to the optimizing calculation of the maximum probability of detection point. It can reduce calculation time and improve calculation accuracy.

Key words:optimal search; gradient; helicopter; dipping sonar

文章编号：1006-0707(2016)04-0118-05

中图分类号：O229

文献标识码：A

doi:10.11809/scbgxb2016.04.029

作者简介：张驰(1990—)，男，硕士研究生，主要从事航空搜潜建模与仿真研究。

收稿日期：2015-09-18；修回日期：2015-10-21

【信息科学与控制工程】