考虑腐蚀影响的钢结构轴压构件可靠度预后分析
李 猛, 麻胜兰, 姜绍飞
(福州大学土木工程学院, 福建 福州 350116)
考虑腐蚀影响的钢结构轴压构件可靠度预后分析
李 猛, 麻胜兰, 姜绍飞
(福州大学土木工程学院, 福建 福州 350116)
摘要:针对腐蚀会严重影响结构的性能甚至使其崩塌失效这一事实, 基于蒙特卡洛方法和Weibull模型提出了钢管轴压构件考虑腐蚀的时变可靠度预测方法. 首先利用幂函数模型替代钢材的实际腐蚀过程计算腐蚀厚度, 其次利用蒙特卡罗方法计算不同年限时的腐蚀钢管轴压构件的可靠度, 同时依据Weibull模型提出钢管在腐蚀作用下的可靠度随时间变化预测曲线. 最后通过实际算例验证了所提方法的有效性. 结果表明: Weibull模型可以较好地模拟腐蚀影响下的可靠度随时间变化的模型; 提出的时变可靠度曲线与理论值吻合较好; 考虑腐蚀影响的可靠度值在一定年限以后将会小于目标可靠度.
关键词:时变可靠性; 腐蚀影响; 钢结构; Weibull模型; 蒙特卡罗方法
0引言
针对当前大型土木结构安全评估的需要, 近些年来一些学者提出了损伤预后(damage prognosis, DP)的学术理念[1-2]. Farrar等[1]认为DP是结构健康监测(structural health monitoring, SHM)未来的主题, 其基本定义是“在结构健康监测系统获得信息和了解损伤演化机理的前提下, 结合结构服役历史和现状, 评估结构当前的损伤状态(第1层次), 预测结构未来的荷载环境和结构性能(第2层次), 并通过数值模拟技术和历史经验来预测结构的剩余使用寿命(第3层次)”[3]. SHM是基于监测数据对当前结构的损伤识别, 而DP是结合历史数据以及当前的信息预测结构未来可能发生的损伤以及预测结构的剩余使用寿命, 需要指出的是, 结构寿命是对“结构失效”而言的, 而“结构失效”有不同的标准, 设计者和结构使用者对待“失效”的态度也不尽相同. 本文从可靠度方面, 即从结构的失效概率方面对结构的失效年限进行研究. 目前针对可靠度的计算方法较多, 如一次二阶矩、 响应面法、 蒙特卡洛方法等[4]. 相比其他的方法, 蒙特卡洛方法可以回避结构可靠度分析中的数学困难, 既可以不考虑功能函数的复杂性, 而且其收敛速度与随机变量的维数无关, 极限状态函数的复杂程度与模拟过程无关, 更无需将状态函数线性化和随机变量“当量正态”化, 具有直接解决问题的能力[5]. 另外, 一些学者在结构的可靠度方面做了相关的研究[6-10], 但这些研究主要基于当前测得的信息对在役结构的现状进行可靠度分析, 而并未预测在役结构在环境腐蚀的影响下其未来某时间点的抗力, 从而无法实现对腐蚀的钢结构的可靠度预后分析的目的.
通过文献可知, 当前预测模型主要有灰色理论、 幂函数、 Weibull模型等. 其中, 灰色理论主要对“外延明确, 内涵不明确”的“小样本、 贫信息”问题具有很好的求解效果, 而幂函数并不适用于具有初始可靠度值的预测, 而Weibull模型常应用于由结构损伤引起的结构性能退化问题, 例如一些学者利用Weibull模型对应力随时间的变化进行拟合, 并且结果较好[11]. 因此本文拟基于蒙特卡洛方法和Weibull模型提出了钢管轴压构件考虑腐蚀的时变可靠度预测曲线, 基于该预测曲线可以对腐蚀的钢结构构件进行可靠度预后分析.
1腐蚀对截面的影响
梁彩凤等[12-14]通过分析17种钢在6个试验站的8 a以及16 a的大气暴露数据, 证实了钢的大气腐蚀发展规律符合幂函数形式, 并且得到了发展幂函数的参数与钢的化学成分和环境因素的定量关系:
(1)
(2)
(3)
式中:D为腐蚀深度(mm);t为暴露时间(a);M、n为常数;M(0)和n(0)是常数;M(i)和n(i)是因子i的系数;Y(i)是因子i的数值. 当因子是钢的化学成分时,Y(i)为钢的化学成分百分比含量, 当因子是环境因素时,Y(i)为环境因子的平均或累积量, 如平均温度. 因子也可以是某个因素的乘方或某几个因素的乘积, 如降雨量乘日照时间. 表1是各影响因素的系数值[14].
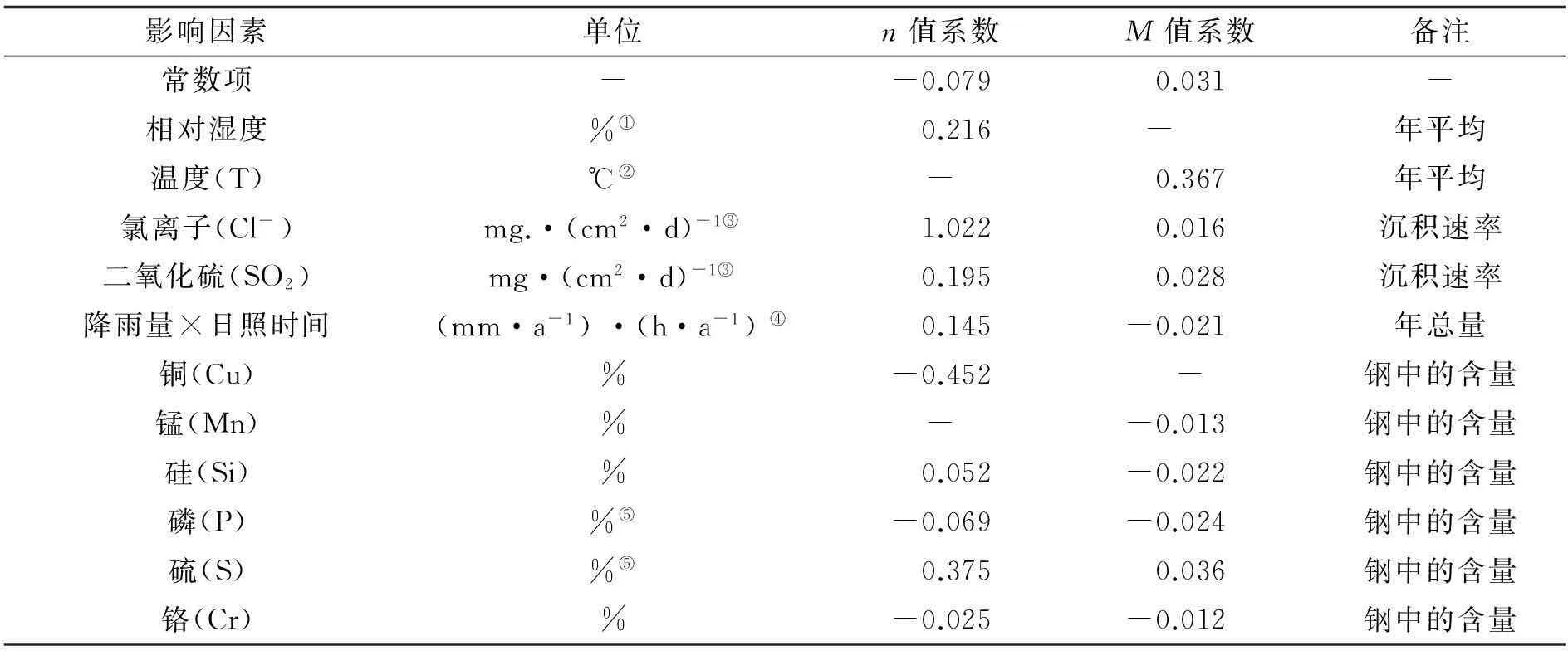
表1 影响因素的系数值
注: 表中各因子Y(i)的单位为实际在发展幂函数的参数与钢的化学成分和环境因素的定量关系中的单位, 在公式(2)、(3)计算中, 各因子Y(i)的单位, 如①相对湿度因子对应为年平均相对湿度值除以100; ②温度因子对应为年平均温度除以100; ③氯离子因子表示该地区每天100平方厘米氯离子含量, 二氧化硫因子同; ④表中降雨量×日照时间因子应该是年降雨总量与每年日照总时间的乘积除以106; ⑤磷因子应该是磷的含量乘以10, 硫同.
2结构可靠度
依据《建筑结构可靠度设计统一标准(GB 50068—2001)》[15], 可靠性是指结构在规定的时间内, 在规定的条件下, 完成预定功能的能力, 而可靠度是指结构在规定的时间内, 在规定的条件下, 完成预定功能的概率, 结构可靠性用可靠度表示. 结构不能完成预定功能的概率, 用pf表示结构失效概率. 考虑到实际工程中对计算失效概率的复杂性, 工程中多采用近似的方法, 即引入了可靠性指标的概念. 极限状态应采用下列极限状态方程描述:
(4)
则功能函数为:
(5)
式中: g(·) 为结构功能函数, Xi(i=1, 2, …, k)为基本变量, 进行可靠度分析时, 即作用效应和结构抗力作为综合的基本变量. 公式(5)表示的是结构的极限状态, 功能函数Z<0和 Z>0分别表示结构失效或是结构安全.
相比其他的可靠度计算方法, 蒙特卡洛法可以回避结构可靠度分析中的数学困难, 既可以不考虑功能函数的复杂性, 而且其收敛速度与随机变量的维数无关, 具有直接解决问题的能力[5], 为此本文利用蒙特卡洛法建立构件可靠度模型.
2.1基于蒙特卡洛方法的可靠度计算
蒙特卡洛方法是一种运用抽样统计理论来近似求解数学或物理问题的方法, 又称为随机模拟方法或统计试验方法. 其具有以下特点: 1)蒙特卡洛方法模拟的收敛速度与基本随机向量的维数无关; 2)极限状态函数的复杂程度与模拟过程无关; 3)无需将状态函数线性化和随机变量当量正态化; 4)数值模拟的误差可由模拟次数和精度较容易地加以确定.
蒙特卡洛方法计算可靠度时, 功能函数Z<0的个数为m, 则在N足够大的情况下, 结构的失效概率可认为:
(6)
依据《建筑结构可靠度设计统一标准(GB 50068—2001)》[15], 结构构件的失效概率与可靠度指标具体下列关系:
(7)
式中:pf为结构构件的失效概率,Φ(·)为标准正态分布函数.
则可靠度指标β
(8)
采用蒙特卡洛直接抽样方法, 计算出失效概率, 然后利用正态分布函数计算出可靠度指标.
2.2时变可靠度
根据蒙特卡洛方法虽然可以计算每年的可靠度指标, 然而这些可靠度指标并不是时间的函数, 无法连续计算任意时间点的可靠度, 这就需要进一步根据计算得到的散点可靠度指标采用合适、 可靠的模型来拟合出一条可靠度的时变曲线.
对于工程结构的寿命模型, 主要有两种模型: Weibull模型[16]以及Frechet模型[17]. Weibull模型可用于因损伤引起的结构性能的退化, 为此本文采用Weibull模型. 其表达为:
(9)
基于此, 本文利用该模型对可靠度随时间变化进行曲线拟合,y为结构的可靠度,t为腐蚀年限,a、b、c、d为拟合常数.
结构按极限状态设计功能函数应符合下式:
(10)
对于公式(5), 若仅有结构作用效应S和结构抗力R两个基本变量时, 则结构功能函数(10)可表示为:
(11)
式中:S为结构的作用效应;R为结构抗力.
本文假定结构的作用效应不变. 在腐蚀环境因素影响下, 结构的抗力会随着服役时间的增加而减小, 即结构的抗力是时变的, 即R(t). 结构的可靠性也会随着服役时间的增加而降低, 因此对服役钢结构的可靠性进行评价, 必须考虑时间变化的影响.
考虑时间的因素, 公式(11)应转化为:
(12)
2.3可靠度预后的计算步骤
1) 选取参数. 选取与功能函数有关的参数. 利用相关理论以及统计方法[18-20]求得, 假设某恒荷载为G, 其标准值为Gk. 一般情况下G 均服从正态分布, 且其平均值μG=kG·Gk, 其中kG=1.06, 相应的变异系数δG=0.074, 本文荷载参数的变异系数取0.07. 同样地, 本文稳定系数的变异系数取0.1, 屈服强度的变异系数取0.08. 根据统计分析可知几何参数随机变量都服从正态分布, 几何参数的设计值可以作为随机变量的均值, 根据统计分析, 杆件长度的变异系数为0.013 5, 外径和壁厚的变异系数为0.035 0.
2) 计算散点可靠度. 利用蒙特卡洛方法并通过Matlab编程, 计算结构在特定年限内不同年限的可靠度指标.
3) 拟合时变可靠度. 采用步骤2)中计算得到的前几年的可靠度值, 通过Weibull模型拟合得出可靠度指标与时间的关系曲线, 即β(t)的计算公式.
4)依据步骤3)的时变可靠度曲线, 结合结构设计的目标可靠度值, 即可对结构的可靠度进行预后分析, 从而达到对结构剩余寿命的预测.
3数值算例
3.1算例概况
本文对厦门某体育馆桁架看台结构的直腹杆钢管构件进行分析, 图1为截面尺寸情况,D为腐蚀厚度,r为钢管壁厚,l为钢管外径. 钢种为20号钢, 暴露在厦门地区50 a的钢管为例, 假设其所受的轴压力为220 KN, 荷载不发生改变. 假定本工况均匀腐蚀, 各基本随机参数服从均匀分布, 构件的基本随机参数以及变异系数[18-20]见表2.
3.2腐蚀对构件截面影响
厦门年平均相对湿度为79%, 平均温度为21 ℃, 年平均降雨量在1 200 mm左右, 日照时间为2 276 h, 二氧化硫含量平均为0.025 mg·m-3, 每天100 cm2氯离子含量为0.35 mg. 选择20号钢, 则依据标准《塑料模具成型部分用钢及其热处理技术条件标准(JB/T 6057—92)》[21]钢的化学成分(质量分数, %)见表3.

表3 20号钢的元素含量化学成分
考虑到20号钢的一些元素的含量在某一范围之中, 因此, 本文取最大值与最小值的平均值, 以及取一些元素的限值. 依据公式(1)~(3)以及表1可计算厦门地区的M为0.057,n的值为0.57, 则公式(1)转化为:
(13)
其中:D为腐蚀深度(mm);t为暴露时间(a).
则不同腐蚀年限下的结构抗力值见下式:
(14)
其中:A(t)为考虑腐蚀影响的截面面积;φ为轴心受压构件的稳定系数;f为钢材的抗压强度设计值.
结合表2和公式(14)不同年限的抗力值, 不同年限的腐蚀钢结构构件抗力值见表4. 从表 4可以看出, 腐蚀的轴压钢构件的抗力随着时间的增加而逐渐降低.
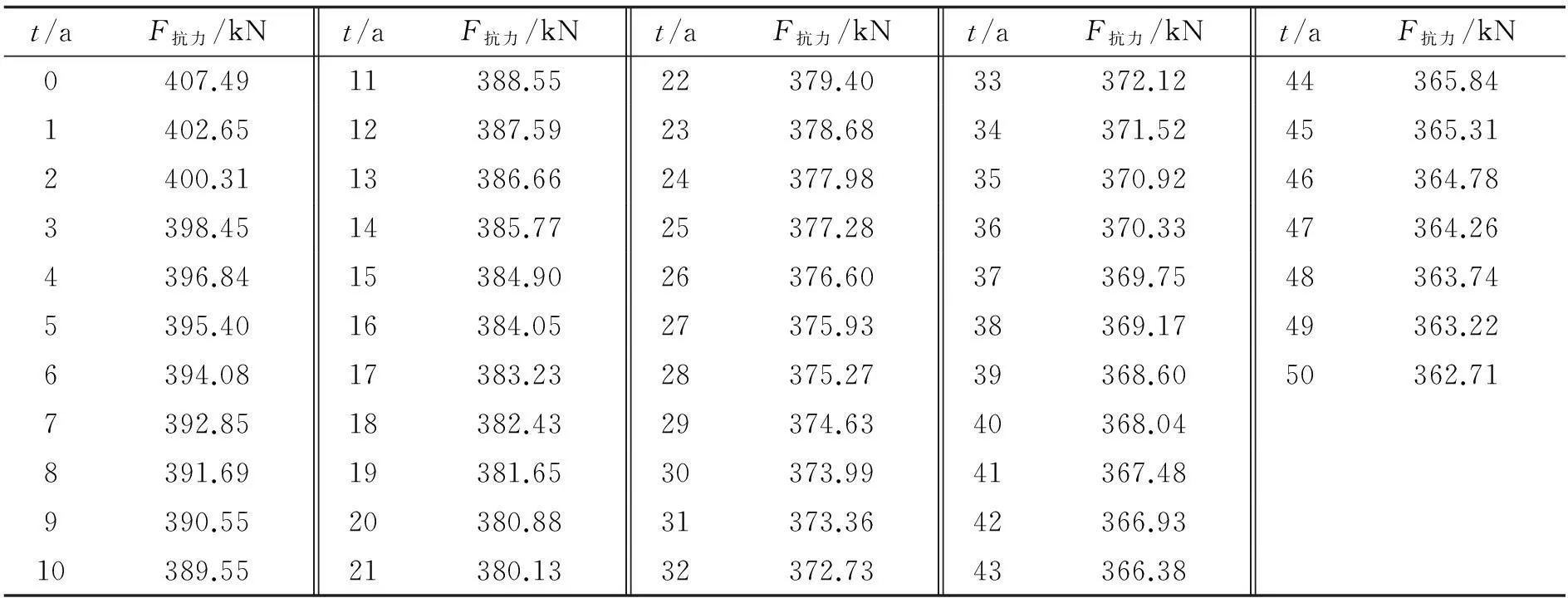
表4 不同年限的腐蚀钢结构构件抗力值
3.3时变可靠度分析
轴心受压构件按下式计算整体稳定[22]:
(15)
式中:F为轴心受压构件的压力设计值;A为构件的毛截面面积;φ为轴心受压构件的稳定系数;f为钢材的抗压强度设计值.
结合3.2节内容, 轴心受压构件的功能函数为:
(16)
式中:A(t)为考虑腐蚀影响的截面面积;φfA(t)为结构的作用效应;F为结构抗力.
根据《建筑结构可靠度设计统一标准(GB 50068—2001)》[15], 假定结构设计使用年限为50 a, 结构安全等级为二级, 延性破坏, 结构构件承载能力极限状态的目标可靠度指标取3.7. 利用蒙特卡罗法计算腐蚀条件下, 不同年限钢构件的可靠度见表5.
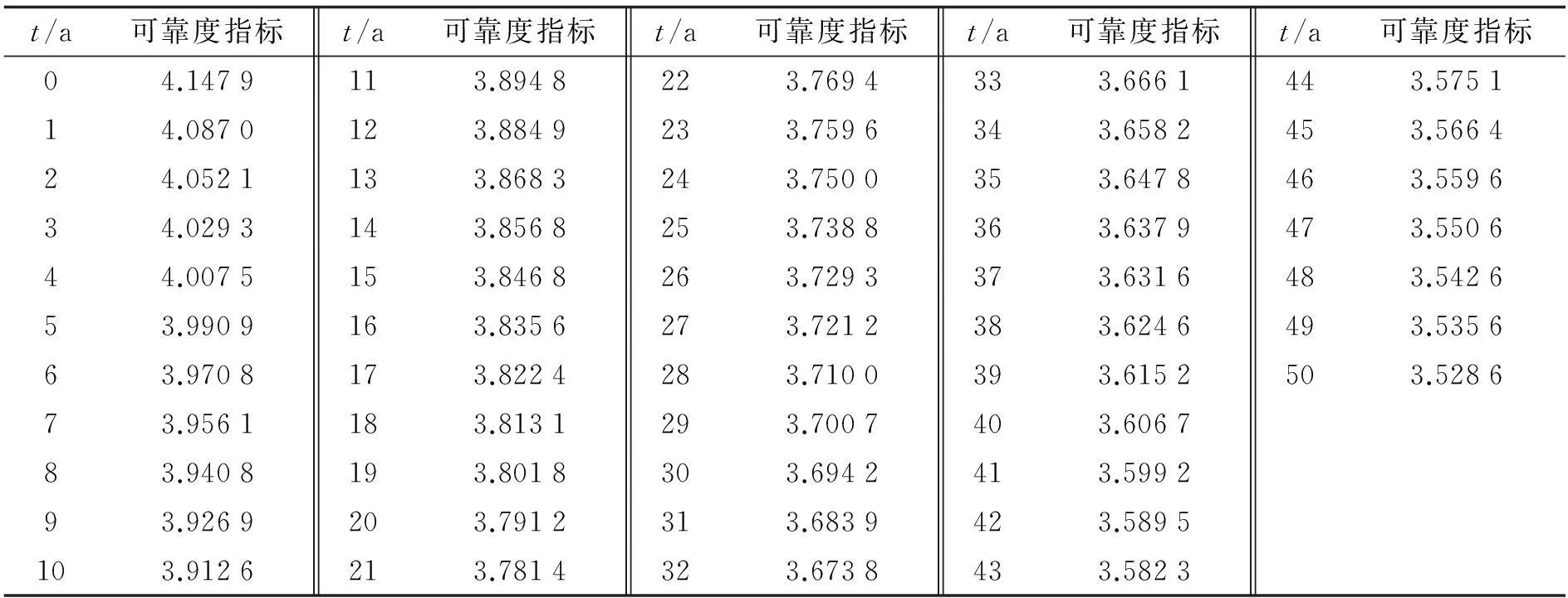
表5 不同年限的腐蚀钢结构构件可靠度
利用Weibull模型对表4中前10 a的可靠度值进行拟合, 得到可靠度与时间的函数表达式:
(17)
其中:a=-4 714.964 384 961 474,b=4 719.109 554 623 710,c=-0.000 012 469 313,d=0.600 175 101 762.t为腐蚀年限(a), 0≤t≤50,β(t)为不同腐蚀年限所对应的可靠度.
3.4可靠度预后分析
当不考虑腐蚀时, 结构的可靠度始终认为是4.147 9, 而考虑腐蚀时, 可靠度值随时间增加而减少. 依据公式(15), 再结合目标可靠度3.7可求出结构的失效年限为29.13 a. 为了更一步验证该方法的有效性, 本文对后40 a的可靠度采用Weibull模型计算的结果与蒙特卡罗模型计算的结果进行比较, 比较结果见图2. 从图中可以看出两种结果基本重合, 说明本文提出的时变可靠度是合理和有效的. 因而, Weibull模型可以很好的对结构因腐蚀损伤而引起的可靠度的进行预后分析.
4结论
结构损伤预后的目的在于将结构的监测结果变为对结构潜在的损伤演化及其后果, 本文从可靠度预后出发, 基于蒙特卡洛方法和Weibull模型提出了钢管轴压构件时变可靠度曲线, 从而对腐蚀轴压钢管构件的可靠度进行预后. 依据Weibull模型提出钢管可靠度随时间变化曲线并与可靠度的理论值和目标可靠度进行了比较. 通过研究得出了以下结论:
1) 本文考虑腐蚀对截面的影响, 腐蚀钢管的抗力随时间逐渐减小, 因此对结构进行时变可靠度分析是对结构体系的一种更加准确的描述.
2) Weibull模型能够很好地预测腐蚀影响的钢结构的时变可靠度. 对本文而言, 通过公式(17), 再结合目标可靠度的值, 即可确定结构的失效年限, 即29.13 a.
3) 本文未考虑腐蚀条件下钢结构构件弹性模量的变化问题, 将在后续的研究中考虑该问题.
参考文献:
[1] FARRAR C R, WORDEN K. An introduction to structural health monitoring[J]. Philosophical Transactions of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2007, 365 (1 851): 303-315.
[2] 李兆霞. 大型土木结构多尺度损伤预后的现状、 研究思路与前景[J]. 东南大学学报(自然科学版), 2013, 43(5): 1 111-1 121.
[3] 宗周红, 钟儒勉, 郑沛娟, 等. 基于健康监测的桥梁结构损伤预后和安全预后研究进展及挑战[J]. 中国公路学报, 2014, 27(12): 46-57.
[4] 赵国藩. 结构可靠度理论[M]. 北京: 中国建筑工业出版社, 2000.
[5] 徐钟济. 蒙特卡洛方法[M]. 上海: 上海科学技术出版社, 1985.
[6] NUH M, SEER T A, TAMIMI A M A,etal. Reliability analysis for degradation effects of pitting corrosion in carbon steel pipes [J]. Procedia Engineering, 2011(10): 1 930-1 935.
[7] CHEN B, XU Y L, QU W L. Corrosion damage assessment and monitoring of large steel space structures[J]. Frontiers of Structural and Civil Engineering, 2010, 4(3): 354-369.
[8] PENG K K, HUANG P Y. Reliability estimating of existing bridge using dynamic Monte Carlo method[J]. Advanced Materials Research, 2010,163/164/165/166/167: 3 156-3 160.
[9] 邵永健, 阎石.型钢混凝土梁受剪承载力的计算及其可靠度分析[J]. 沈阳建筑大学学报(自然科学版), 2006, 22(4): 579-583.
[10]金宏忠, 高巍, 来猛刚. 基于模型试验的既有梁桥体系可靠度计算方法[J]. 沈阳建筑大学学报(自然科学版), 2011, 27(4): 636-641.
[11] 肖南, 王海, 陈华鹏, 等. 大气腐蚀下网架结构症状可靠度及寿命预测[J]. 浙江大学学报(工学版), 2013, 47(8): 1 373-1 378.
[12] 梁彩凤, 侯文泰. 碳钢及低合金钢8年大气暴露腐蚀研究[J]. 腐蚀科学与防护技术, 1995, 7(3): 183-186.
[13] 梁彩凤, 侯文泰. 碳钢、 低合金钢16年大气暴露腐蚀研究[J]. 中国腐蚀与防护学报, 2005, 25(1): 1-6.
[14] 梁彩凤, 侯文泰. 钢的大气腐蚀预测[J]. 中国腐蚀与防护学报, 2006, 26(3): 129-135.
[15] 中华人民共和国建设部. 建筑结构可靠度设计统一标准: GB50068-2001[S]. 北京: 中国建筑工业出版社, 2001.
[16]CEMPEL C. Theory of energy transforming systems and their application in diagnostics of operating systems[J]. Applied Mathematics in Computer Science, 1993(3): 553-548.
[17]CEMPEL C. Passive diagnostic experiment, symptom reliability and their application in vibration condition monitoring[J]. Zagadnienia Eksploatacji Maszyn, 1990, 2(3): 343-355.
[18]王淇, 何喜年. 基于蒙特卡罗法的钢框架结构可靠度计算方法的研究[C]// 2008年度全国钢结构学术年会论文集. 北京:[s.n.], 2008: 55-59.
[19]彭立新.结构可靠性管理-预测、 控制与评定[M]. 北京: 中国建筑工业出版社, 2012.
[20]贡金鑫, 魏巍巍. 工程结构可靠性设计原理[M]. 北京: 机械工业出版社, 2007.
[21]中华人民共和国国家发展和改革委员会, 中国机械工业联合会. 塑料模具成型部分用钢及其热处理技术条件标准: JB/T 6057—1992[S].北京: 机械工业出版社, 1992.
[22]中华人民共和国建设部. 钢结构设计规范:GB 50017—2003[S]. 北京: 中国计划出版社, 2003.
(责任编辑: 林晓)
Reliability prognosis analysis on axial compressed members of steel structures with corrosion into consideration
LI Meng, MA Shenglan, JIANG Shaofei
(College of Civil Engineering, Fuzhou University, Fuzhou, Fujian 350116, China)
Abstract:Corrosion is one kind of damage or failure modes occurred frequently in steel structures, which can usually lead to structural deterioration and even collapse failure. Therefore, this paper proposes a time-dependent reliability analysis approach by integrating Monte Carlo method and Weibull model. More specifically, the power function is firstly used to replace the practical steel corroding process in order to calculate the section area under corrosion; secondly, Monte Carlo method is used to calculate the reliability of axial force members of corrosion steel structure; simultaneously, the Weibull model is utilized to fit the forecast curve of reliability-time; finally, a practical simulation is performed to validate the proposed method. The results show that: Weibull model can effectively simulate the time-dependent reliability process in the corrosion environment; the proposed time-dependent reliability analysis results are in a good agreement with theoretical values; and reliability value of the proposed method will be smaller than the target reliability value of design structural presented.
Keywords:time-dependent reliability; corrosion effect; steel structure; Weibull model; Monte Carlo method
中图分类号:TU391; TU312.3
文献标识码:A
基金项目:国家自然科学基金资助项目(51278127); 国家科技支撑计划资助项目(2015BAK14B02)
通讯作者:姜绍飞(1969-), 教授, 主要从事结构健康监测与组合结构研究, cejsf@fzu.edu.cn
收稿日期:2015-07-09
文章编号:1000-2243(2016)02-0259-07
DOI:10.7631/issn.1000-2243.2016.02.0259

