具反馈控制和Holling-II类功能性反应的修正Leslie-Gower捕食系统的持久性
王 颖, 陈江彬
(1. 阳光学院基础教研部, 福建 福州 350015; 2. 福州大学至诚学院, 福建 福州 350002)
具反馈控制和Holling-II类功能性反应的修正Leslie-Gower捕食系统的持久性
王 颖1, 陈江彬2
(1. 阳光学院基础教研部, 福建 福州350015; 2. 福州大学至诚学院, 福建 福州350002)
摘要:研究具有反馈控制变量和Holling-II类功能性反应的修正Leslie-Gower捕食系统的持久性问题, 运用微分不等式得到一组新的保证该系统持久的充分性条件. 该结果表明反馈控制变量不会影响系统的持久性, 从而改进了已有的结果.
关键词:反馈控制; Holling-II类功能性反应; 修正Leslie-Gower; 持久性
0引言
对定义在[0, +∞)上的任一有界连续函数f(t), 本文恒设:
2003年, Aziz-Alaoui和Daher Okiye[1]提出并研究了如下具有修正Leslie-Gower项和Holling II类功能性反应的捕食食饵系统:
得到该系统的有界性和正平衡点的全局稳定性. Yu[2]进一步利用振动性引理和Lyapunov函数法给出两个保证正平衡点全局稳定的充分性条件, 修正了文[1]的结果; Song等[3-4]探讨了在脉冲干扰效应下的该类自治和非自治系统的稳定性和持久性; Zhu和Wang[5]讨论了该类非自治周期系统的周期解的存在性和全局稳定性. 考虑到自然界会受到人类的开采等因素的影响以及非自治系统更能精确的描述实际情况, 文[6]提出并研究了如下具反馈控制非自治的修正Leslie-Gower和Holling II功能性反应的捕食系统:
(1)
其中: ri(t), ai(t), ci(t), ei(t), di(t), b1(t)(i=1, 2) 均为有正的上下界的连续函数; x(t)和y(t)分别表示种群x和y在t时刻的密度; u(t), v(t)为反馈控制变量, 该系统其余各系数的生物学含义见文[1]. 在假设系统(1)满足初值条件: x(0)>0, y(0)>0, u(0)>0, v(0)>0的情况下, 通过运用适当的分析手法, 文[6]得到了如下关于持久性的结论:
Zhu和Wang[5]研究了在无反馈控制变量即ci=ei=di=0且ki(t)=ki(i=1, 2), ki为常数的情况下系统(1)所对应的系统
(1’)
在假设各系数均为T-周期函数的情况下, 通过运用重合度理论, 他们得到了如下结论:
作为Teng[13]的定理2的直接推论, 根据定理2, 可以得到:
1主要引理及证明

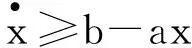
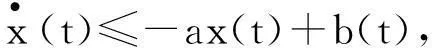
下面分三个引理给出定理2的证明.
引理4[6]设(x(t), y(t), u(t), v(t))T为系统(1)的任一正解, 则有:
(2)
由引理4可知, 对上述ε, 存在T>0, 使得对任意的t≥T, 有
x(t)≤M1+εM1ε, y(t)≤M2+εM2ε, u(t)≤M3+εM3ε, v(t)≤M4+εM4ε
当t≥T时, 由系统(1)的第一个方程可知
(3)
对(3)式两端从τ(τ≤t)到t积分得
(4)
由系统(1)的第三个方程可知
(5)
由式(4)、 (5)及引理3得, 对任意的0≤s≤t, 有
(6)
(7)
对上述K, 存在T1≥T+K, 当t≥T1时, 由(6)式可得
(8)
当t≥T1时, 由式(2)、 (7)、 (8)及系统(1)的第一个方程可知:
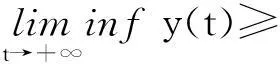
注2: 引理6的证明与引理5的证明类似, 为了阅读的方便, 也将该证明简略给出.
证明由引理4可知, 对任意ε>0, 存在T>0, 使得对任意的t≥T, 有
x(t)≤M1+εM1ε, y(t)≤M2+εM2ε, u(t)≤M3+εM3ε, v(t)≤M4+εM4ε
当t≥T时, 由系统(1)的第二个方程可知
(9)
对(9)式两端从τ(τ≤t)到t积分得
(10)
由系统(1)的第四个方程可知
(11)
由式(10)、 (11)及引理3得, 对任意的0≤s≤t, 有:
(12)
(13)
对上述H, 存在T1≥T+H, 当t≥T1时, 由(12)式可得
(14)
当t≥T1时, 由式(13)、 (14)及(1)的第二个方程可知,
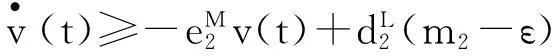
注3: 显然定理2与定理1相比条件弱化了很多, 说明研究结果实质性地改进了文[6]的主要结果. 而且定理2的条件与反馈控制变量无关, 说明系统(1)的持久性与反馈控制变量无关.
2应用举例
本节通过举例验证结果的可行性.
例1考虑如下系统:
(15)
对应于系统(1), 有:
由引理4可知,


即定理1的条件不满足, 所以根据定理1是没办法得到持久性的结论, 故本文结果极大地改进了文[6]的结果.
3结论
本文研究了具有反馈控制变量和Holling-II类功能性反应的修正Leslie-Gower捕食系统的持久性问题, 通过运用微分不等式得到了一组保证该系统持久的充分性条件. 所得结果显示该系统的持久性确实与反馈控制变量无关, 从而改进了文[6]的结果. 通过对比推论1和定理3, 可知本研究简化了Zhu和Wang[5]的结论条件, 改进了文[5]的结果.
参考文献:
[1]AZIZ-ALAOUI M A, DAHER OKIYE M. Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type II schemes[J]. Applied Mathematics Letters, 2003, 16 (7): 1 069-1 075.
[2]YU S B. Global asymptotic stability of a predator-prey model with modified Leslie-Gower and Holling-type II schemes[J]. Discrete Dynamics in Nature and Society, 2012(6): 857-868.
[3]GUO H J, SONG X Y. An impulsive predator-prey system with modified Leslie-Gower and Holling type II schemes[J]. Chaos, Solitons and Fractals, 2008, 36(5): 1 320-1 331.
[4]SONG X Y, LI Y F. Dynamic behaviors of the periodic predator-preymodel with modified Leslie-Gower Holling-type II schemes and impulsive effect[J]. Nonlinear Analysis: Real World Applications, 2008, 9(1): 64-79.
[5]ZHU Y L, WANG K. Existence and global attractivity of positive periodic solutions for a predator-prey model with modified Leslie-Gower Holling-type II schemes[J]. Journal of Mathematical Analysis and Applications, 2011, 384 (2): 400-408.
[6]李忠. 具反馈控制修正Leslie-Gower和Holling-II功能性反应捕食系统的持久性和全局吸引性[J]. 数学的实践与认识, 2011, 41(7): 126-130.
[7]CHEN F D, YANG J H, CHEN L J. Note on the persistent property of a feedback control system with delays[J]. Nonlinear Analysis: Real World Applications, 2010, 11(2): 1 061-1 066.
[8]CHEN F D, YANG J H, CHEN L J,etal. On a mutualism model with feedback controls[J]. Applied Mathematics and Computation, 2009, 214(2): 581-587.
[9]阮育清, 杨慧涛. 具有反馈控制和时滞的“食物有限”单种群模型的持久性[J]. 福州大学学报(自然科学版), 2012, 40(2): 160-164.
[10]CHEN F D, LI Z, HUANG Y J. Note on the permanence of a competitive system with infinite delay and feedback controls[J]. Nonlinear Analysis: Real World Applications, 2007, 8(2): 680-687.
[11]YU S B, CHEN F D. Almost periodic solution of a modified Leslie-Gower predator-prey model with Holling-type II schemes and mutual interference[J]. International Journal of Biomathematics, 2014, 7(3): 81-95.
[12]YU S B. Global stability of a modified Leslie-Gower model with Beddington-DeAngelis functional response[J]. Advances in Difference Equations, 2014(2): 1-14.
[13]TENG Z D. The almost periodic Kolmogorov competitive systems[J]. Nonlinear Analysis: Theory, Methods & Applications, 2000, 42(7): 1 221-1 230.
(责任编辑: 林晓)
Permanence of a modified Leslie-Gower Holling-type II predator-prey system with feedback controls
WANG Ying1, CHEN Jiangbin2
(1. Department of Basic Teaching and Research, Sunshine College, Fuzhou, Fujian 350015, China;2. Zhicheng College, Fuzhou University, Fuzhou, Fujian 350002, China)
Abstract:A modified Leslie-Gower predator-prey system with Holling II response function and feedback controls is studied. By applying the differential inequality theory, sufficient conditions which guarantee the permanence of the system are obtained. The results indicate that feedback control variables have no influence on the persistent property of the system. Our result not only supplement but also improve some existing ones.
Keywords:feedback controls; Holling-II esponse function; modified Leslie-Gower; permanence
中图分类号:O175.14
文献标识码:A
基金项目:福建省教育厅A类资助项目(JA11294)
通讯作者:王颖(1980-), 讲师, 主要从事概率论与数理统计等方面研究, wangyingcd@163.com
收稿日期:2013-07-30
文章编号:1000-2243(2016)02-0150-06
DOI:10.7631/issn.1000-2243.2016.02.0150

