基于灰关联分析的模糊C均值算法

李莉琼， 刘漳辉， 郭 昆

(福州大学数学与计算机科学学院， 福建 福州　350116)



基于灰关联分析的模糊C均值算法

李莉琼， 刘漳辉， 郭 昆

(福州大学数学与计算机科学学院， 福建 福州350116)

摘要：标准的模糊C均值算法(FCM)采用欧式距离测度， 均等地利用所有特征来计算数据间的相似性， 但其存在受局部特征影响、 对非球状簇识别效果不佳、 无法适应高维数据等缺点. 为此， 提出一种将基于差异信息理论的灰关联分析结合到FCM中的新算法， 利用均衡接近度描述数据间的相似性， 强调从整体上判断数据的相似程度， 减弱局部特征高关联性的影响， 能够适应不同形状簇的识别. 在人工和真实数据集上的实验表明， 所提出的新算法具有更高的聚类精度和更好的稳定性.

关键词：模糊C均值算法； 灰关联分析； 均衡接近度； 差异信息理论； 灰色方法

0引言

随着信息技术的不断发展和大数据时代的来临， 通过聚类从数据中挖掘有价值的信息越来越受到人们的关注. 聚类作为一种在类别信息未知的条件下， 根据对象间的相似性将其划分为不同的簇， 使簇内对象相似性高于簇间对象相似性的方法， 已经被应用于机器学习、 工程学、 生物学、 统计学、 社会科学和经济学等诸多领域[1].

FCM算法允许每个对象同时隶属于多个簇， 从而能够更客观地反映现实世界中对象类属的模糊性， 是目前应用较广泛的一种聚类算法[2]. 然而， FCM算法也存在对初始值的选择比较敏感、 容易陷入局部极值、 不能自动确定聚类的类别数等问题. 针对这些不足， 近几年来人们陆续提出了多种改进的FCM算法. Das[3]提出了FCM算法在模式识别中的应用， 分析了采用欧式距离以及其他度量方式的算法在相同数据集下的比较分析， 得出了不同度量方式下的算法性能； Winkler等[4]提出在高维空间中的模糊C均值算法， 通过观察目标函数值的变化， 可以减弱数据维数对于聚类算法的灾难影响， 解决了陷于局部极值的初始化等问题， 给出了适合高维数据的FCM算法的条件； Fan等[5]提出一种固定的抑制率选择方法的模糊C均值算法， 该方法与数据本身的结构信息相结合， 为每个数据选择出固定的抑制率， 从而使得聚类的效果更好； Niu等[6]提出一种基于PSO的改进模糊C均值算法， 该算法先按照数据与中心点间的距离进行分配， 然后通过优化策略进行优化， 克服了对噪声点敏感、 过早收敛等问题； Hamasuna Y等[7]针对错误值、 缺失属性等数据提出用惩罚向量对其进行处理， 然后采用基于Mahalanobis距离的模糊C均值对其进行聚类， 通过实验证明该方法具有一定的有效性； Kao L J等[8]提出一种自适应的FCM算法, 根据欧几里得距离得到点与类之间的离群度， 如果大于预设阈值则检测出离群点且删除, 一定程度上减弱了离群点的影响， 得到更好的类中心； 任丽娜等[9]提出基于自适应权重的模糊C均值聚类算法SAWFCM， 该算法通过动态的赋予每个样本对于类的权重， 从而降低了算法对初始类中心的依赖； 吴小燕等[10]提出联机局部自适应模糊C均值聚类算法OLAFCM， 该算法通过为各特征赋以权重， 有效降低了采用全局降维方法造成的信息损失且具有更好的性能； 侯薇等[11]提出一种基于隶属度优化的演化聚类算法， 该算法采用抽样的方式产生较好的初始聚类中心， 且通过更新小隶属度操作实现了对FCM算法的加速； 韩敏等[12]提出一种单点逼近型加权模糊C均值算法SWFCM, 该算法通过先验样本单点逼近的方法来消除先验样本选取的影响， 从而得到合适的初始聚类中心. 虽然这些改进算法从不同方面提高了FCM算法的性能， 但在处理信息差异方面还存在一些不足. 聚类算法中相似性的度量是影响聚类结果的重要因素， 因此从相似性度量的角度出发结合已有的FCM算法展开研究.

灰色系统理论是由邓聚龙[13]在1982年提出的一种研究和处理少数据、 贫信息等不确定性问题的系统理论， 已经被广泛应用于众多领域. 灰关联分析是灰色理论中一个重要组成部分， 具有假设条件少、 处理手段丰富、 注重数据自身信息、 灰生成变换后的数据能一定程度抵御噪声干扰等特点， 因此在聚类算法中得到很好的应用. 首先， FCM算法对样本进行聚类， 得到的聚类中心被当作标准模式矩阵， 然后计算被检查模式和标准模式之间的灰色关联度， 从而很好地发现转子的不平衡状况. 本文给出一种基于灰关联分析的FCM改进算法， 利用灰关联分析采用均衡接近度作为相似性度量方式的优势， 有效弥补FCM算法处理信息差异的不足， 同时提高了FCM算法的聚类精度和稳定性.

1灰关联分析

灰色系统理论内容丰富， 主要包括灰生成、 灰分析、 灰建模、 灰预测等方面的内容[13-14]. 灰关联分析是灰色系统分析中的一个重要的内容， 它对样本的数量和分布规律不做要求， 量化结果与定性分析的结果保持一致， 因此特别适用于对小样本、 无明显规律的数据进行研究.

1.1传统的灰关联分析

为了消除数据中存在的噪声， 弱化其随机性， 显示其规律性， 在进行灰色关联分析前， 通常需要利用灰序列生成算子对原始数据进行处理， 生成灰序列. 目前已经提出多种序列生成算子. 其中， 区间值生成算子应用较为广泛， 其定义如下：

定义1区间值生成算子. 设序列Xi=(xi(1), xi(2), …, xi(n))为因素Xi的行为序列， D为序列算子， XiD =(xi(1)d, xi(2)d,…, xi(n)d)

其中：

(1)

则称D为区间值化算子.

定义2灰色关联系数. 对于一个参考数列X0有若干个比较数列X1,X2, …,Xn， 则称

(2)

为Xi对X0在第k点的灰关联系数， Δ0i(k)为Xi对X0在第k点的绝对差值. Δ(min)为最小绝对差， Δ(max)为最大绝对差. 其中, ρ为分辨系数， ρ>0， 通常取0.5.

定义3灰关联度. 若存在一个非负实数γ (x0(k), xi(k)) 为X 上一定环境下的比较测度， 且令非负实数

(3)

则当其满足规范性、 偶对称性、 整体性、 接近性时， 称γ(X0,Xi)为Xi对X0的灰关联度.

1.2基于差异信息理论的灰关联分析

张岐山[15]提出灰朦胧集的差异信息理论通过在灰关联分析中引入灰关联熵， 以均衡接近度作为衡量标准， 克服了传统灰关联分析可能造成局部特征关联倾向的问题.

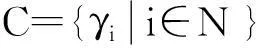
(4)

为灰关联系数分布映射， 映射值v(x0(k), xi(k))为第i个比较序列在第k点的灰关联密度值. 此比较序列的所有灰关联密度值的全体构成灰关联密度序列， 记为vi.

(5)

为第i个比较序列的灰关联熵.

定义 6熵关联度. 设I(vi)为第 i个比较序列的灰关联熵， Im为灰关联系数序列的最大关联熵， 则称

(6)

为第i个比较序列的熵关联度.

定义7均衡接近度. 设γ(X0, Xi)和E(X0, Xi)分别为第i个比较序列的灰关联度和熵关联度， 则称

(7)

为第i个比较序列的均衡接近度.

2基于灰关联分析的FCM算法

2.1标准FCM算法

标准FCM算法通过优化公式(8)定义的目标函数实现数据点的聚类[16]：

(8)

其中： Ci为类中心， dij为第i个聚类中心与第j个数据点间的欧式距离， μij满足

(9)

通过优化目标函数(8)得到下面的迭代更新条件[16]：

(10)

2.2基于灰关联分析的FCM算法

采用欧氏距离作为两点间的相似性度量， 没有考虑到局部特征的偏差影响. 对于多维数据而言， 对每一维特征都要充分的考虑， 否则容易受差异性较大的局部特征的影响， 从而得不到精确的聚类结果. 灰关联分析的另一个优势是从整体上考虑数据点之间的相似度， 从而能够发现整体分布相似的数据点， 克服欧式距离只从特征值相近程度考虑数据点相似度的局限.

从第1节中的理论分析和公式的推导可以发现， 基于差异信息理论的均衡接近度通过计算数据点间的熵关联度， 能够有效降低局部特征关联倾向对数据点相似度的影响.

因此， 采用下面基于灰关联分析的距离测度代替常用的欧式距离测度.

(11)

其中：i=1, …,c;j=1, …,n,B(Ci,Xj)是第j个数据点对类别i的均衡接近度.

结合标准FCM算法的思想， 得到一种新的基于灰关联分析的FCM算法GFCM(FCM based on grey relational analysis ).

输入： 聚类类别数c、 数据集 (大小为n)、 迭代终止阈值ε、 模糊因子m、 灰色关联系数的分辨系数ρ

输出： 数据集的聚类结果

GFCM算法的步骤如下：

1) 规范化数据. 用公式(1)处理原始数据， 生成相应的序列算子.

2) 初始化隶属度矩阵. 用区间[0, 1]上的随机数初始化隶属度矩阵U， 并保证其满足公式(9)中的约束条件.

3) 更新聚类中心Ci. 用公式(10)计算c个聚类中心Ci， i=1, …, c.

4) 更新隶属度矩阵U. 用公式(11)计算dij， 将其代入公式(10)得到下次迭代需要的隶属度矩阵U=[uij]，i=1, …,c;j=1, …,n.

5) 用公式(8)计算目标函数的值， 若与上次迭代得到的目标函数的差值小于阀值ε， 则算法结束， 否则转至步骤3).

2.3复杂度分析

首先分析GFCM算法的时间复杂度. 构建数据矩阵需要O(n×d)的时间， 计算任意两个属性序列的均衡接近度的时间复杂度为O(d)， 因此构建隶属度矩阵需要的时间为 O(c×n×d). 设最大迭代次数为Cmax， 则GFCM算法总的时间复杂度为O(Cmax×c×n×d)， 其中c为类别数， n为数据集大小， d为特征维数.

接下来分析算法的空间复杂度. 数据矩阵占用空间为O(n×d)， 隶属度矩阵占用空间为O(c×n)， 类中心矩阵占用空间为O(c×d). 一般c, d << n， 则算法总的空间复杂度为O(max(c, d)×n).

3实验与结果分析

实验是在人工数据集和真实数据集上完成的， 人工数据集采用高斯函数生成， 真实数据集是从UCI中选取的6个有代表性的数据集. 数据集的详细信息如表1所示.

表1　实验数据集

表1中： μ和δ是高斯函数中的均值和标准差参数； n表示数据集的大小； d表示数据集的特征维数； c表示数据集的类别数. 每个类别中心μ的取值范围为[0, 10]， 且任意两个类中心的距离≥2， δ取0.5， 从而在保证各类别数据点存在一定分离度的同时， 又使相邻类别的数据点存在一定程度重叠， 获得更好地检验算法识别重叠类数据的能力. 人工数据集的大小从500变化至50 000， 以检验不同规模数据对算法性能的影响.

实验在硬件配置为处理器 Intel(R) Celeron(R) CPU 1.8GHz、 内存2GB， 软件配置为Windows 7操作系统、 Microsoft Visual C++ 6.0的平台上展开. 实验中参数的设置为： 聚类类别数c(表1所示的类别数)、 迭代终止阈值ε=10-4、 模糊因子m=2、 灰色关联系数的分辨系数ρ=0.5.

实验分别从算法精确度、 特征维数影响方面对GFCM算法、 FCM算法、 SAWFCM算法[9]、 OLAFCM算法[10]进行比较分析. 由于FCM算法存在随机性， 取每个算法在每个数据集上20次运行的平均值作为实验结果. 算法精确度采用F测度指标.

定义8F测度：

(12)

(13)

其中: T(i)表示正确分到第i个类的实例数；Cluster(i) 表示第i个簇的实例数；Class(i) 表示第i个类的实例数.

3.1精确度的实验结果

F测度的实验结果如图1和图2所示.

从图1可以看出， 在人工数据集上， GFCM算法总是优于其他三种对比算法， 表明基于均衡接近度的相似性测度能够很好地处理数据间地差异性， 更真实的反映数据之间蕴含的规律. 从图2可以看出， 在真实数据集上， GFCM算法在iris和spamebase数据集上稍显劣势之外， 在其他数据集上都优于对比算法， 说明在多变的真实应用环境中， 基于均衡接近度的相似性度量在总体上比其他对比算法的相似性度量更能真实反映数据之间的相似性， 从而获得较好的聚类结果. 然而， 对于那些比较依赖空间距离划分数据点的数据集， 灰关联度可能不是非常适合， 可以考虑将其与欧式距离相结合， 这将是下一步的工作.

3.2特征维数影响的实验结果

为了检验数据特征维数变化对算法性能的影响， 通过调整人工数据集的维数参数对算法在不同特征维数下的精确度进行了实验. 考虑到数据集大小对算法精确度的影响， 实验时分别取大小为500和5 000的数据集进行了测试. 此次实验的数据集与实验3.1中人工数据集的生成方式相同， 同样是通过高斯函数随机生成的. 实验结果分别如图3和图4所示.

从图3和图4中可以看出， 在不同规模的数据集中， 随着维数的增加， GFCM算法在不同特征维数的数据集上的实验结果保持不变的情况下略有波动， 说明GFCM算法的性能受维数影响较小， 具有一定的稳定性； 其次， GFCM算法对不同特征之间的差异信息进行处理， 通过调整不同特征对聚类的影响， 从均衡接近度的角度出发刻画数据点之间的整体相似性， 和其他三种算法对比， 能够得到较高精度的聚类效果， 适用于不同特征维数的数据聚类.

4结论

通过介绍标准FCM算法和灰关联分析的基本概念及将其引入FCM算法的优势， 提出一种新的基于灰关联分析的FCM算法， 并分析了算法的时间和空间复杂度. 最后， 通过在人工数据集和真实数据集上的实验， 证明了提出的算法能够有效克服局部特征值高关联性影响、 高维性能差等缺陷， 以均衡接近度作为数据相似性测度， 得到了更高精度的聚类结果.

参考文献：

[1]贺玲, 吴玲达, 蔡益朝. 数据挖掘中的聚类算法综述[J]. 计算机应用研究, 2007, 24(1): 10-13.

[2]严骏. 模糊聚类算法应用研究[D]. 杭州: 浙江大学, 2006.

[3]DAS S. Pattern recognition using the fuzzy C-means technique[J]. International Journal of Energy, Information and Communications, 2013, 4(1): 1-14.

[4]WINKLER R, KLAWONN F, KRUSE R. Fuzzy C-means in high dimensional spaces[J]. International Journal of Fuzzy System Applications, 2011, 1(1): 1-16.

[5]FAN J, LI J. A fixed suppressed rate selection method for suppressed fuzzy C-means clustering algorithm[J]. Applied Mathematics, 2014, 5(8): 1 355.

[6]NIU Q, HUANG X. An improved fuzzy C-means clustering algorithm based on PSO[J]. Journal of Software, 2011, 6(5): 873-879.

[7]HAMASUNA Y, ENDO Y, MIYAMOTO S. On Mahalanobis distance based fuzzy C-means clustering for uncertain data using penalty vector regularization[C]//IEEE International Conference on Fuzzy Systems. Taipei: IEEE, 2011: 810-815.

[8]KAO L J, HUANG Y P. A robust fuzzy clustering method with outliers influence free[C]// International Conference on Fuzzy Theory and it's Applications. Taichung: IEEE, 2012: 342-347.

[9]任丽娜, 秦永彬, 许道云. 基于自适应权重的模糊 C-均值聚类算法[J]. 计算机应用研究, 2012, 29(8): 2 849-2 851.

[10]吴小燕, 陈松灿. 联机局部自适应模糊 C 均值聚类算法[J]. 模式识别与人工智能, 2013, 26(11): 1 026-1 032.

[11]侯薇, 董红斌, 印桂生. 一种基于隶属度优化的演化聚类算法[J]. 计算机研究与发展, 2013, 50(3): 548-558.

[12]韩敏, 范剑超. 单点逼近型加权模糊 C 均值算法的遥感图像聚类应用[J]. 中国图象图形学报, 2009 (11): 2 333-2 340.

[13]DENG J L. Control problems of grey system[J]. System and Control Letter, 1982,1(5): 288-294.

[14]刘思峰, 谢乃明. 灰色系统理论及其应用[M]. 北京: 科学出版社, 2008.

[15]张岐山.灰朦胧集的差异信息理论[M].北京： 石油工业出版社， 2002.

[16]BEZDEK J C. Pattern recognition with fuzzy objective function algorithms[M]. New York: Plenum Press, 1981.

(责任编辑： 林晓)

Fuzzy C-means based on grey relational analysis

LI Liqiong， LIU Zhanghui， GUO Kun

(College of Mathematics and Computer Science, Fuzhou University, Fuzhou， Fujian 350116, China)

Abstract:Fuzzy C means algorithm using the Euclidean distance measure uses all the characteristics to calculate the similarities between the data points equably, which has disadvantages of the local characteristics' impact and poor identification of aspherical clusters and poor adaptability of high-dimensional data points, etc. In this paper, a novel algorithm that integrated the grey relational analysis based on differential information theory with the FCM algorithm was proposed. The similarities between the data points were described by the balanced closeness degree, which emphasized on judging similarities on the whole and attenuated the impact of the high similarities of the local characteristics and adapted to identify clusters of different shapes. The experimental results on the artificial and real-world datasets demonstrate that the proposed algorithm achieves both high clustering accuracy and good stability.

Keywords:fuzzy C means; grey relational analysis; balanced closeness degree; differential information theory; grey methods

中图分类号：TP391

文献标识码：A

基金项目：国家自然科学基金资助项目( 61103175, 61300104)； 教育部科学技术研究重点项目( 212086)； 福建省科技创新平台建设资助项目(2009J1007)； 福建省自然科学基金资助项目( 2013J01230)； 福建省高校杰出青年科学基金资助项目(JA12016)； 福建省高等学校新世纪优秀人才支持计划资助项目(JA13021)

通讯作者:刘漳辉(1971-)， 副教授， 主要从事智能网络技术研究， liliqiong0712@163.com

收稿日期:2014-05-22

文章编号：1000-2243(2016)02-0170-06

DOI:10.7631/issn.1000-2243.2016.02.0170