基于改进ADPP的多变量时间序列异常检测
董红玉, 陈晓云
(福州大学数学与计算机科学学院, 福建 福州 350116)
基于改进ADPP的多变量时间序列异常检测
董红玉, 陈晓云
(福州大学数学与计算机科学学院, 福建 福州350116)
摘要:针对多变量时间序列异常检测问题进行研究, 提出基于改进ADPP的多变量时间序列异常检测算法IADPP. IADPP算法引入适用于多变量时间序列的张量相似性度量SSOTPCA, 并以此相似性度量构造序列集的k-近邻图, 在构造的k-近邻图上计算多变量时间序列的异常系数. 研究结果表明, IADPP算法克服了原有ADPP算法不支持多变量时间序列和要求密度均匀的缺陷, 取得了较好的检测结果.
关键词:多变量时间序列; 异常检测; 张量相似性度量; k-近邻图
1相关研究
多变量时间序列MTS(multivariate time series)是指多个变量依照时间先后顺序得到的一系列观察值的集合, 记为Xi(t), (i=1, 2, …m; t=1, 2, …n). 其中i表示变量个数(m≥2), t表示序列长度. 它可用一个n×m的矩阵表示如下:
(1)
MTS数据广泛存在于各种应用领域, 如视频监控、 金融、 医疗、 气象、 动作捕捉等.
异常检测是指在数据集中发现不符合期望行为的数据点, 这些不符合期望行为的数据点在不同的应用领域被称为异常, 孤立值, 不和谐的观察值, 奇异模式等[1]. 异常检测作为数据挖掘领域的重要分支, 在医学诊断、 信用卡欺诈、 网络入侵、 生态系统失调等领域有着强大的实际应用背景, 而这些领域的数据类型一般都是或能转化为MTS数据, 因此, 针对MTS的异常检测研究有较强的实践意义.
根据异常的表现形式, 异常可分为全序列异常和子序列异常, 当子序列的长度为1时, 子序列异常退化为点异常. 本文针对多变量时间序列的全序列异常, 即异常样本展开研究.
根据采用技术的不同, 现有MTS异常检测方法可分为以下5类:
1) 基于统计的异常检测. 指为数据建立一个模型, 与模型参数拟合概率较低的对象判为异常. 文献[2]提出的基于核主成分分析KPCA(kernel principal component analysis)的异常检测算法, 通过KPCA获取MTS的主方向矢量并估计训练样本vMF(von miser-fisher)分布模型的参数, 将小概率的测试样本归为异常. 该算法预先设定数据满足vMF分布, 但真实数据的分布一般较为复杂且不一定满足vMF分布. 文献[3]和文献[4]分别采用投影寻踪和独立成分分析确定序列的峰度系数, 样本的峰度系数和模型预定的系数范围比较广. 但这两种方法均单独处理每个变量, 忽视了变量间的相关性.
2) 基于距离的异常检测. 是指若一个对象远离其它大部分数据点, 就认为该对象是异常的, 其中远离程度通过距离度量. 文献[5]提出基于解决集的子序列异常检测算法, 通过滑动窗口获得MTS子序列并用扩展的Frobenius范数(Eros)[6]计算子序列间的距离, 根据距离的大小采用基于解决集的方法检测异常. 虽然该类方法简便易行, 但它对距离的选择异常敏感, 且不适用密度分布不均的数据集.
3) 基于密度的异常检测. 是指若一个对象的密度相对于其它对象较低, 那它就被判定为异常, 对象的密度(局部异常系数)表明了该对象与其它对象的相似程度. 该类方法是对基于距离异常检测方法的改进, 能较好地处理具有不同密度的数据集. 文献[7]和[8]都是基于此思想, 不同的是文献[7]采用Eros计算样本间的相似性, 而文献[8]采用SPCA[9]计算相似性, 但这两种相似性度量均不满足三角不等式.
4) 基于聚类的异常检测. 是将规模较小的簇内对象或簇隶属度较低的对象判定为异常. 文献[10]提出两阶段的异常检测算法, 通过有界坐标系统计算样本相似性, 采用K-means算法对数据聚类并由一个启发式规则对其排序, 最后在簇上采用循环嵌套算法进行异常检测, 该算法严重依赖簇个数, 而且时间复杂度较高.
5) 基于图的异常检测. 先构造一个样本连接图, 之后将连接图中与其它样本连接较少的对象定义为异常. 如文献[11]提出的基于随机游走的MTS异常检测算法, 先采用高斯径向基函数获得数据集每个变量的相似度矩阵, 并把相似度矩阵转化为样本连接图, 之后通过随机游走算法计算各样本的连接系数, 以此判断样本的异常程度. 但该算法将MTS的变量分别处理, 忽视了变量间的相关性.
目前, 基于图的异常检测方法也成为目前异常检测领域的研究热点. 文献[12]提出基于邻近图和PageRank的异常检测算法—ADPP(anomalydetectionusingproximitygraphandPageRank), 该算法先构造了样本的ε-邻域图, 之后利用PageRank算法[11]发现图中的异常样本. 经实验验证, 该方法提高了异常检测的准确率, 但ADPP算法仅适用向量型数据, 不适用于矩阵型的MTS数据. 本文拟对ADPP算法进行适当改进, 使其能成功应用于MTS数据.
2PageRank及ADPP算法简介
PageRank算法[13]最早由Page和Brin提出, 被Google用于网页排名, 可看做在定向图上的马尔可夫随机游走模型:
(2)
ADPP算法[12]则先构造一个ε-邻域图, 在图上执行改进的PageRank.ε-邻域图的构造原理如下: 若两样本点落在ε-邻域内, 边的权值定义如下:
(3)
式中:dist(xi, xj)表示样本点xi和xj的欧氏距离; 反之, wij=0.
转移矩阵P根据构造的ε-邻域图定义:
(4)

传递向量C依据每个样本点的权值定义, 其元素
(5)
此外,ADPP算法通过下式计算J
(6)
由上述可知, ADPP算法主要包括以下四个步骤:
Step 1计算数据集内各数据点间的欧式距离dist(xi, xj)并储存;
Step2给定阈值ε, 若dist(xi, xj)≤ε, 根据式(3)计算数据点间边的权值, 记为权值矩阵W;
Step 3分别由式(4)和(5)计算数据集的转移矩阵P和传递向量C;
Step 4由式(6)计算连接度J, 并对J值升序排列, 将J值较小的数据点判定为异常.
ADPP算法的不足在于: ①构造ε-邻域图时使用全局阈值, 因此ADPP算法对数据集密度分布情况依赖程度高. ②由式(6)可知, 求解J的过程两次用到逆矩阵, 计算一个d×d矩阵的逆矩阵的时间复杂度高达O(d3), 这导致了ADPP算法的时间开销较大.
3IADPP 检测算法
针对ADPP算法不适用MTS数据及要求数据集密度分布均匀, 提出基于改进ADPP的多变量时间序列异常检测方法—IADPP. IADPP算法引入支持多变量时间序列的张量相似性度量SSOTPCA, 构造时间序列集的k-近邻图, 新的k-近邻图可以有效避免原有ADPP算法ε-邻域图对数据集密度敏感的问题.
3.1相关定义
定义1张量相似性度量SSOTPCA.
(7)

定义2样本X的k-相似度(simk(X)).
给定一个自然数k和MTS数据集D, 样本X的k-相似度是X和数据集D中的某个样本Z之间的相似度, 记为simk(X). 样本Z满足以下两个条件:
1) 至少存在k个样本Z′∈D{X}, 使得SSOTPCA(X, Z′)≥SSOTPCA(X, Z′);
2) 至多存在k-1个样本Z′∈D{X}, 使得SSOTPCA(X, Z′)≥SSOTPCA(X, Z′).
对于MTS数据集D={X1, X2, …, Xd}, 通过样本的simk(X)构造样本间的k-近邻图. 近邻图是关于样本的加权图G=(V, E), 其中V表示顶点集, E表示边集, 若样本Xi与Xj存在边当且仅当SSOTPCA(Xi, Xj)≥simk(Xi), 那么边的权值wij≥0. 权重矩阵W定义如下:
(8)
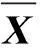

定义3MTS样本异常系数.
MTS样本的异常系数ODi(i=1, …, d)定义为对应连接度的倒数:
(9)
如果样本的异常系数较大, 就意味着样本与其它样本的连接度较小, 从而样本为异常的概率就较大.
定义4MTS数据集的相对异常样本.
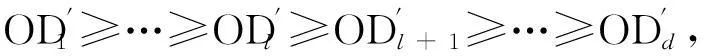
3.2基于改进ADPP的异常检测算法描述
算法名称: 基于改进ADPP的异常检测算法.
输入: MTS样本的数据集D, 近邻数k, 输出样本数l, 阻尼系数α, 阈值β, 最大迭代次数t.
输出: 前l个异常样本.
Step 1利用张量相似性度量SSOTPCA计算MTS样本的k-相似度simk(X);
Step 2构造关于数据集D的k-近邻图, 并计算图中边的权值矩阵W;
Step 3分别由式(4)和(5)计算样本转移矩阵P和传递向量C;
Step 4由式(2)采用循环迭代算法计算MTS样本的连接度Ji(i=1, …,d);
Step 5由式(9)计算样本的异常系数ODi(i=1, …,d), 对所有样本的异常系数降序排列;
Step 6输出异常系数最大的前l个MTS样本.
4实验与结果分析
4.1实验数据集
选取两组MTS数据集进行实验, 分别为JV2和Wafer2, 表1概要描述了这两组实验数据.

表1 实验数据概述
JV2数据集选取了JV 数据集[13]中第三个测试者的118个样本作为正常类, 第五个测试者的前10个样本作为异常类. Wafer2数据集随机选择Wafer数据集[14]中normal类的190个样本, abnormal类的10 个样本作为测试集.
4.2三种异常检测算法性能比较
实验比较以下3种算法的检测准确率及时间开销:
1) IADPP算法: 基于张量相似性度量SSOTPCA构造k-近邻图.
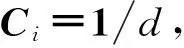
3) T_ADPP算法: 基于张量相似性度量SSOTPCA构造ε-邻域图.
当传递向量C取均值时, 由经验定义阻尼系数α=0.85. 为了实验的可比较性, 三种算法均取阻尼系数α=0.85, 输出样本数l=10. IADPP算法设阈值β=0.001, 最大迭代数t=20. 分别在JV2和Wafer2数据集上实验, 实验结果见表2.
由表2可知: 对于JV2和Wafer2数据集, IADPP算法的检测准确率明显高于IADPP_M和T_ADPP算法. 这是因为IADPP_M算法的传递向量没有考虑到序列集的权值, 平等看待每个样本; 而T_ADPP算法的ε-邻域图依赖数据集的密度分布. 此外, 在JV2数据集上, 若T_ADPP算法取邻域ε=1.5时, 求解过程出现奇异情况, 无法得到正确的结果.

表2 三种异常检测算法在两组数据集上的检测准确率
下面比较在以上参数条件下这三种算法的时间开销. 实验结果如图1所示. 由图1可知, 时间开销从小到大排列依次是 IADPP_M、 IADPP、 T_ADPP算法. 从理论上讲, 由于IADPP_M算法的传递向量直接定义为均值向量, 不需要计算, 而IADPP和T_ADPP算法的传递向量都是根据权值矩阵计算, 故IADPP算法时间开销要比IADPP_M算法大; T_ADPP算法求解逆矩阵的时间复杂度为O(d3),d为样本数, IADPP算法采用迭代算法的时间复杂度O(t),t为迭代次数, 因此IADPP算法的时间开销低于T_ADPP算法.
综合比较IADPP、 IADPP_M和T_ADPP三种算法在两组数据集上的检测准确率和时间开销可知, IADPP算法不仅有较高的检测准确率, 其时间开销也比T_ADPP算法小.
4.3参数对IADPP算法的影响
IADPP算法阈值β和最大迭代数t影响算法的时间开销, 而样本近邻图的近邻数k和阻尼系数α影响算法的检测准确率. 本文只讨论近邻数k和阻尼参数α对算法准确率的影响, 实验分别在JV2和Wafer2数据集上进行, 结果如图2所示.
由图2(a)可知: 随着近邻数的增加, IADPP算法的准确率逐渐提高, 当近邻数增加到一定程度后, 准确率保持不变. 由此可知, 在构造k-近邻图时, 直接取较大的近邻数k, 能在一定程度上保证IADPP算法的准确率. 选择上述实验准确率最高时所对应的最小近邻数, 即JV2数据集取k=20, Wafer2数据集取k=10. 由图2(b)可知: 随着阻尼系数α的增加, IADPP算法的准确率始终保持不变. 这说明IADPP算法对阻尼系数α不敏感.
5结语
针对ADPP异常检测算法不适用MTS数据及要求数据密度分布均匀, 提出基于改进ADPP的多变量时间序列异常检测算法IADPP. 该算法基于逆向挖掘思想, 即异常样本肯定是与其它样本连接度最低的样本, 引入支持MTS的张量相似性度量, 并以此度量构造样本的k-近邻图, 在新的k-近邻图上计算MTS的异常系数. 在真实数据集上的实验结果表明算法能取得较好的检测结果.
参考文献:
[1]VARUN C, ARINDAM B, KUMAR V. Anomaly detection for discrete sequences: a survey[J]. IEEE Transactions on Knowledge and Data Engineering, 2012, 24(5), 823-839.
[2]李权, 周兴社. 基于KPCA的多变量时间序列数据异常检测方法研究[J]. 计算机测量与控制, 2011, 19(4): 822-825.
[3]GALEANO D, PENA R, TSAY R S. Outlier detection in multivariate time series by projection pursuit[J]. Journal of the American Statistical Association, 2006, 101(474), 654-669.
[4]BARAGONA R, BATTAGLIA F. Outlier detection in multivariate time series by independent component analysis[J]. Neural Computation, 2007, 19(7): 1 962-1 984.
[5]WENG X, SHEN J. Finding discordant subsequence in multivariate time series[C]//2007 IEEE International Conference on Automation and Logistics. Piscataway:IEEE, 2007: 1 731-1 735. DOI:10.1109/ICA L.27.4338852.
[6]YaNG K, SHAHABI C. A PCA-based similarity measure for multivariate time series[C]//Proceedings of the Second ACM International Workshop on Multimedia Databases. Washington:ACM, 2004: 65-74. DOI:10.1145/1032604.1032616.
[7]翁小清, 沈钧毅. 多变量时间序列异常样本的识别[J]. 模式识别与人工智能, 2007, 20(4): 463-468.
[8]郭小芳, 李锋, 宋晓宁. 一种基于PCA的时间序列异常检测方法[J]. 江西师范大学学报(自然科学版), 2012, 36(3): 280-283.
[9] SINGHA A , SEBORG D E. Pattern matching in historical batch data using PCA[J]. IEEE Control Systems Magazine, 2002, 22(5): 53-63.
[10]王欣.两阶段的多元时间异常检测算法[J]. 计算机应用研究, 2011, 28(7): 2 466-2 469.
[11]CHENG H B, TAN P N, POTTER C,etal. A robust graph-based algorithm for detection and characterization of anomalies in noisy multivariate time series[C]// Workshops Proceedings of the 8th IEEE International Conference on Data Mining.Pisa:IEEE, 2008: 349-358. DOI:10.1109/ICDMW.2008.48.
[12]YAO Z, MARK P, RABBAT M. Anomaly detection using proximity graph and PageRank algorithm[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(4): 1 288-1 300.
[13]PAGE L, BRIN S, MOTWANI R,etal. The PageRank citation ranking: bring order to the web[R].Stanford: Stanford University, 1998.
[14]PageRank[EB/O L].[2013-04-23]. http://en.wikipedia.org/wiki/PageRank.
(责任编辑: 蒋培玉)
Outlier detection based on improved ADPP for multivariate time series
DONG Hongyu, CHEN Xiaoyun
(College of Mathematics and Computer Science, Fuzhou University, Fuzhou, Fujian 350116, China)
Abstract:We study the outlier detection for multivariate time series, and an approach of outlier detection for multivariate time series based on improved ADPP-IADPP is proposed. IADPP algorithm introduces tensor similarity measure SSOTPCAsupporting for multivariate time series, and constructs the k-neighbor graph about the sequence set. Then, we calculate the outlier coefficient of multivariate time series on k-neighbor graph .The research results show that the proposed method overcomes the disadvantages that original ADPP does not support multivariate time series and requests uniform density, IADPP algorithm achieves a better detection results.
Keywords:multivariate time series; outlier detection; tensor similarity measure; k-neighbor graph
中图分类号:TP311
文献标识码:A
基金项目:福建省新世纪优秀人才资助项目(XSJRC2007-11)
通讯作者:陈晓云(1970-), 教授, 主要从事数据挖掘、 机器学习、 模式识别等研究, c_xiaoyun@21cn.com
收稿日期:2013-09-10
文章编号:1000-2243(2016)02-0164-06
DOI:10.7631/issn.1000-2243.2016.02.0164

