基于最大最小蚁群算法的多卸载点车载装箱模型研究

田 冉,孙林夫,唐慧佳,李斌勇

(西南交通大学 信息科学与技术学院，四川 成都 610031)

基于最大最小蚁群算法的多卸载点车载装箱模型研究

田 冉,孙林夫,唐慧佳,李斌勇

(西南交通大学 信息科学与技术学院，四川 成都 610031)

针对多卸载点、多种货物、多车承运中的箱式货车装箱问题，为需要在不同地点卸货的货物生成货物装卸序列。建立了基于体积、重量和装卸距离的数学模型，定义了各类装箱约束条件，首先按照装箱规则和装箱约束生成一个可行解作为蚁群算法的初始解，再根据蚂蚁在货物上寻路的特点定义了信息素和选择概率公式，通过最大最小蚁群算法在一定的循环次数内求得最优解，从而达到最大化货车的装载利用率和体积利用率的目标。最后通过一个实例证明了该方法的合理性和有效性。

交通工程；多卸载点；车辆装箱；最大最小蚁群算法

0 引 言

三维装箱问题(Three-Dimensional Bin Packing Problem，3D-BPP)是一类复杂的具有约束条件的组合优化问题，在理论上属于NP完全问题[1]。

国内外的专家学者对装箱问题进行了大量的研究。研究内容主要可以分成两种：①建立在简化模型的基础上，并未考虑在现实中实际存在的多目标和多约束的布局，仅是研究三维布局中的优化方法。如：K.A.Dowsland等[2]和F.G.Ortmann等[3]对装箱中的布局问题进行了描述性工作，其中大部分是研究二维或三维的布局优化方法，目前常见的优化方法有数学规划法、图论法、启发式方法、人工智能等方法；T.G.Crainic等[4]提出了一种二级禁忌搜索算法；O.D.Lara等[5]提出了基于蚁群算法的多目标求解算法；张德富等[6]提出了一个求解装箱的混合模拟退火算法，通过复合块的生成，基础启发式算法和模拟退火算法来寻找问题的近似最优解；Huang Wenqi等[7]提出了通过穴度方法求解一类装箱问题的算法。卫家骏[8]在装箱问题的降序最先适应算法和降序最优适应算法的基础上，提出了一个改进的降序最优适应的集装箱船配载算法。连志刚等[9]建立了符合集装箱装载实际的数学模型，并利用类粒子群算法对所建模型进行优化，实现了容器容积和承重量的最大发挥。②建立在多目标和多约束布局的基础上，如：曹玲芝[10]探讨了混合模拟退火算法在集装箱装载过程中的多目标、多约束优化的问题；靳志宏等[11]提出了一种GW节约算法与基于剩余空间的装箱算法有机结合的交互式算法，并分别与配载优先和配送优先的单独优化进行了对照仿真实验。

这些研究中对集装箱装箱研究较多，对货车装箱的研究很少。需要指出的是车辆装箱和集装箱装箱的并不一样：集装箱装箱的一次性需要装入的货物类型较少，货物的体积重量差别不大，且没有在运输过程中装卸的需求；但是车辆装箱正好相反，例如：在汽车配件的运输过程中，需要装箱的货物体积、重量类型差别较大，而现有的研究并未有一个完整考虑体积、重量、装卸顺序的多种约束的方法来解决这一问题。同时对于汽车配件运输来说，一车货物可能有多个卸载点是实际存在的，但在多卸载点的研究大多集中在车辆线路规划和车辆调度上，对于多卸载点的车辆该如何装箱研究很少，因此研究多卸载点的车辆如何装箱具有实际意义和应用价值。

针对这一问题，笔者构建了包含货物体积、重量和装卸顺序的厢式货车装箱模型，在最大最小蚁群算法基础上设计了相应的求解算法以求得最优的装货顺序，并通过实例验证了该模型的有效性。

1 问题描述

笔者主要针对多种货物、多卸载点、多车承运中的装箱问题进行研究。可定义为：有大量的多种长方体货物需要通过多个货车运到多个卸载地点，为了方便货物卸载，需要在装车时满足先“先上后下”的原则，同时需要在货物完全装入货车后通过不同的摆放顺序以满足如下的各个约束，最终需求的承运车辆最少，需要的承运成本最低。在这一过程中定义如下约束：

1) 装载货物必须完全包含在车辆之中；

2) 装载货物的总体积和总重量不能超过车辆的容积和承重；

3) 任何两个装载货物之间不能相互重叠；

4) 装载货物必须水平放置，即不能斜放；

5) 装载的货物不能悬空放置，即必须放在其它可压货物上或者托盘上；

6) 必须保证货车的稳定性，即装载货物后的货车重心必须限制在一定的范围内；

7) 货物必须满足“先上后下”的原则。

由于问题的复杂性，同时进行约定：

1) 货物为同一类型，即不存在化学品和食物混装的现象；

2) 忽略货物的挤压变形，即只要货物是可压的就不会有变形现象出现；

3) 任意货物的重心都为其几何中心；

4) 不存在货物颠倒放置的现象出现；

5) 约定所有的货物都为规则的矩形件；

6) 约定货车或者货物的长≥宽≥高；

7) 所有的货物都是可压的；

8) 货车仅从车辆尾部进行卸货；

9) 所有货车的型号相同。

2 数学模型

2.1 基本变量定义

采用坐标系为三维笛卡尔坐标系，以货车车辆的长度方向为x轴，宽度方向为y轴，高度方向为h轴，车辆的左后下角为坐标原点(0，0，0)。设定k辆车辆的长宽高分别为Lk，Wk，Hk；所装货物t的长宽高分别为lt，wt，ht，如图1。

图1 货车装箱各参数定义Fig.1 The definition of truck packing parameters

2.1.1 货物t的表示

货物t可以用一个11元组(n，Ct，At，k，zt，xst，yst，zst，xet，yet，zet)来表示货物装车后的状态。其中：C为货物类型；A为卸货地点；t为货物ID；k为承运车辆ID；放置方向和空间方位则由后7位 (zt，xst，yst，zst，xet，yet，zet)表示。

当zst=1时，货物t的长和货车k的x轴平行，且宽与y轴平行；当zst=0时，货物t的长和货车k的y轴平行，且宽与x轴平行。货物t的位置坐标为货物t在货车k内的左后下角坐标[0]-(xst，yst，zst)和右前上角坐标[4]-(xet，yet，zet)。例如：在图1中货物t的空间方位可以表述为(0，0，0，lt，wt，ht)。

2.1.2 货物装入车辆的情况

当货物装入车辆时后会产生3个尺寸和形状不同的新的剩余空间(V1，V2，V3)[12]，所在位置分别处于图1中已放入货物t的(1)，(2)，(3)的3个方向。

剩余空间可以由6个字段的信息来描述，分别为剩余空间的左后下角的坐标和右前上角的坐标。例如在图1中：当货车k未装载货物时的剩余空间则可以描述为Vk=(0，0，0，Lk，Wk，Hk)，其中：Lk，Wk，Hk分别为货车装载空间的长、宽、高。

在装载过程中的剩余空间则定义为

Vl=(xd,yd,zd,xu,yu,zu)l=1,2,…,|V|

式中：|V|为当前可用的剩余空间的个数。

2.1.3 货车的载重信息

货车的载重信息定义为Gk(第k辆车的最大承载重量)，货车的承运信息表示为

2.1.4 货物卸载的优先级确定

对每个货物按照其卸货地点的远近定义其卸载优先级：

λt=Dt/Dmax

式中：Dt为货物t从配送点到卸货地点的距离； Dmax为待装的所有货物从配送点到卸货地点的最远距离，货物卸载地点越远其装入的优先级越高。

2.2 装箱约束条件

在实际的装箱过程中会有很多约束条件，这里对各项约束进行定义：

1) 货物t必须装入车辆k内，不能超过车辆的边界

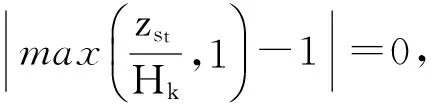
2) 装载货物的总体积和总重量不能超过车辆的容积和承重

3) 任何两个装载货物(t,r)之间不能相互重叠

4) 装载货物必须水平放置，即不能斜放：

ztk∈{1,0},∀t∈{t|qtk=1}

5) 货物不能悬空放置：

∀t∈{t|zst>0,qtkl=1}；

∃r,r∈{r|qrk=qtk,zer=zet,xsr≤xst,xer≥xet,ysr≤yst,yer≥yet};

6) 货物必须满足先上后下的原则

货物的装卸约束定义为：对于货物t和货物r，如果λt≥λr，必有xst≤xsr。

货车装载需要在多个地点卸货的货物时，卸货地点相同的货物的装卸优先级相同，因此需要对同一地点卸货的货物进行装载优化；当货物优先级不同时，则需要满足先上后下的卸载原则，因此必须满足xst≤xsr。同时由于货车车厢大都为后门卸货，因此在同一y轴上的货物即使卸载优先级不同也不影响货物装卸，所以y轴上不存在类似约束。而在z轴上，由于同一优先级的货物可以重叠放置，因此z轴上也不存在类似约束。

7) 重心约束

货车上放置货物需要满足车辆行驶安全的需要，因此需要满足：

其中：(XGmin,XGmax),(YGmin,YGmax),(HGmin,HGmax)分别对应在x轴，y轴和高度h方向上的车辆重心的安全范围。(xt,yt,ht)为货物t的重心坐标。这里将车辆的重心近似为：

2.3 目标函数和适应度函数的定义

货物装车的主要目标是在车辆最少的情况下装入全部待装货物，使得货车的容积利用率和重量利用率最大，同时保证货物的装卸序列满足多地点装卸时先上后下的要求。笔者这里定义了3个目标函数：

2.3.1 空间利用函数

(1)

式中：Vt表示已经装车的货物t的体积，t∈[1，mj]；mj表示车辆j上所有装车的货物数量；CVj中j∈[1，n]表示第j辆车的容积。

2.3.2 重量利用函数

(2)

式中：Wt表示已经装车的货物t的重量；CWj表示车辆j的承载重量。

2.3.3 装卸距离函数

D=∏dt

(3)

如果：λt≥λr，有xst≤xsr；则：dt=1，否则dt=0。t，r∈[1，mj]，且t≠r。

2.3.4 适应度函数

在满足装卸一体化的条件下，为了最大化空间利用率和重量利用率，定义适应度函数为

F()=(CR+WR)×D

(4)

只有在满足装卸的条件下，即装卸距离函数D不为0时，再最大化空间利用率和重量利用率。

3 算法设计

货物的装载本身是一种组合优化问题，存在多种不同的组合方式，其主要目标就是如何在其中寻找适应度函数最大的最优解。而蚁群算法是一种基于群体的元启发式算法，由M．Dorigo等[13]于1992年首先提出。目前蚁群算法以其正反馈，分布式等优点已经成功的应用于多个NP难的组合优化问题的求解，因此笔者将蚁群算法作为解决组合优化问题的办法来解决装卸一体化的装箱问题。

但是由于蚁群算法[14]最初使用的是随机策略确定寻路路径，使得进化速度和收敛速度较慢，因此笔者通过两个阶段来实现蚁群的路径寻优：一阶段为首先通过在满足装卸约束的条件下按货物卸载优先级从大到小和体积从大到小的原则求初始的可行解；二阶段为在初始可行解的基础上，根据重新定义了初始分配信息素、信息素挥发公式和选择概率公式，再通过最大最小蚁群算法来寻找最优解。在蚁群算法寻找最优解的过程中不再随机定义蚂蚁的出发点，而是按照装箱的特性固定为体积最大、运输最远的箱子为出发点。在信息素的挥发过程中再按照箱子上次的排序进行挥发，排序靠前的箱子挥发较少。在选择箱子的过程中按照能见度和信息素的差异进行选择，尽可能的选择体积较为一致的箱子统一摆放。

3.1 求初始的可行解

一阶段算法流程：

Step1:初始化车辆及货物的相关信息，按照货物的卸载优先级从大到小进行排序，货物装卸优先级相同的货物则按照货物体积从大到小进行排序。

Step2:在卸载优先级较大的待装货物集合中选择体积最大的货物体积和当前车辆等待装入的剩余空间体积比较，如果货物体积小于剩余空间体积，则放入货物并更新待装货物集合和剩余空间集合，否则选择体积次大的货物进行比较。如果优先级最小、体积最小的最后一个待装货物的体积都大于车辆剩余空间体积，则增加运输车辆，返回Step1继续。当待装货物集合为空时，装箱完成。

最后得到的装箱顺序即为一个初始解。但由于只考虑了货物的卸载优先级和体积大小，结果并不一定完全满足在2.2节中定义的各项约束，因此该初始解是一个可行解，但并非是一个强可行解，其为蚁群算法寻找最优的强可行解打下了基础。

3.2 蚁群算法寻找最优解

这里不再如传统的蚁群算法将信息素定义在各条子路径上，而是将信息素定义为每个货物的属性，即将待装的货物看作是蚂蚁需要寻路的路径，货物的装箱顺序即为蚂蚁的寻路路径。同时每次循环都是由多只蚂蚁顺序执行寻路操作，和传统蚁群算法将不同蚂蚁放到不同的点上开始寻路的方式不同，文中每只蚂蚁的起点均为所有待装货物中的卸载优先级最大和体积最大的货物。因为首先装入的货物是固定的，必然是体积最大、运输最远的。不同于传统蚁群算法均分初始信息素，笔者将寻路顺序定义在每个货物的信息素中，将3.1节的初始装箱算法所生成的解作为蚁群算法的初始解，以货物的装箱顺序分配初始信息素，以所有的货物都装完作为一次蚂蚁寻路完成的标志。

3.2.1 初始信息素定义

定义货物t上的初始信息素τt为

(5)

3.2.2 信息素的更新

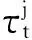
(6)

(7)

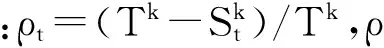
3.2.3 选择概率

选择概率为蚂蚁在选择了货物t之后选择下一个货物r的概率：

(8)

ηtr为能见度，定义为

(9)

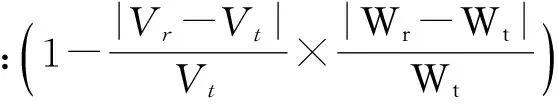
3.2.4 算法流程

二阶段算法流程：

Step1：初始化最大循环次数n，蚂蚁数量m，最大信息素τmax，最小信息素τmin；

Step2：初始化待装货物信息和车辆信息，根据3.1小节中求得初始解；

Step3：根据初始解，按照式(5)为每个货物分配初始信息素；

Step4：在一次循环内，蚂蚁按照选择概率式(8)完成一次寻路，选择下一个需要装入的箱子时通过约束条件1)～6)判断是否能够装入车辆，如果不能则增加车辆，返回step2；

Step5：如果该蚂蚁的寻路路径为当前最优路径，则按式(6)更新信息素，否则按式(5)更新信息素。所有蚂蚁一次寻路完成后，本次循环结束，本次循环的最优路径作为下次循环的初始解，返回step3；

Step6：循环次数达到最大循环次数时终止，输出当前最优路径为最优解。

4 计算结果

车辆装箱和集装箱装箱的选择数据类型的不同点在于：集装箱装箱的一次性需要装入的货物类型少，且体积重量差别不大，但需要装入的数量很多，没有运输过程中中途装卸的需求。但车辆装箱正好相反，在汽车企业配件运输的过程中，需要装箱的货物类型是根据配件的大小，货物的体积、重量类型差别较大，且有运输过程中中途装卸的需求。

笔者选择的测试数据为某汽车厂备件中心一次发给承运商的承运单信息，一共有4种不同类型的货物，且有中途装卸的需求，有4个目的地。可以总结为有7种、共50个货物需要发往4个地方。货物数量不多的原因是承运单上一次不会有超出车辆装载性能十几倍的装箱需求，一般都是物流车辆承受能力的1～3倍，是可以让承运商承受的装运信息。货物的相关数据如表1。

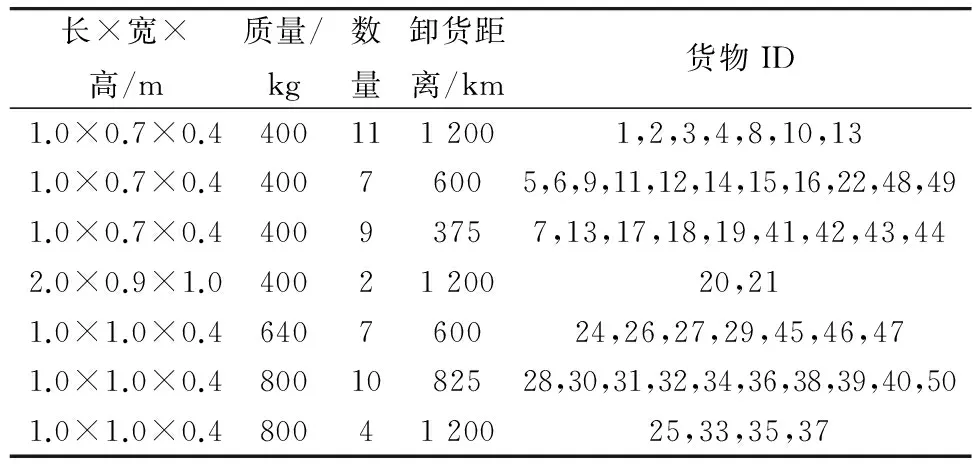
表1 装箱数据contentTable 1 Packing data

测试参数选择为：共30只蚂蚁，循环最大次数为120次。车辆为中型后开门货车，长宽高为5 m×2 m×2 m，最大承载重量为25 t。由于需要装车的货物总体积大于该类型货车可装箱的总体积，因此该订单需要两节货车进行装载。由于无论采用何种装箱方法都必须满足货物必须装完的必要约束条件，且总有一辆车是未满载的状态，因此无论何种算法，在装完所有货物后的总的车辆利用率肯定是一样的。因此这里仅比较第一辆的车的装箱评价数据，即使得第一辆车的体积利用率、重量利用率在满足装卸条件和运输约束等条件下尽可能最大。评价数据越大则说明第一辆车的利用率越高，装箱顺序越合理。使用3.1节中的算法流程生成的可行解，可行解中包含了车辆1和车辆2的装箱顺序内容，其中车辆1的装箱单如表2。

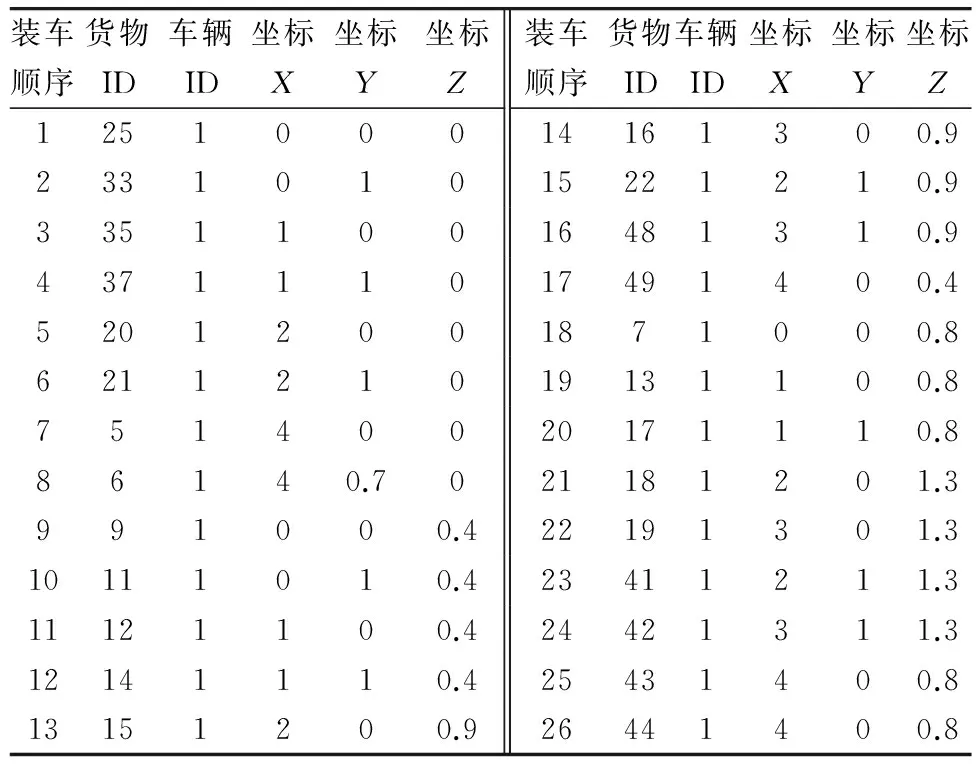
表2 车辆1的初始装箱单Table 2 Initial packing list of car1

将该结果运用到3.2节中的蚁群算法中求最优解，通过100次循环得到每次循环的最优装箱结果如图2。

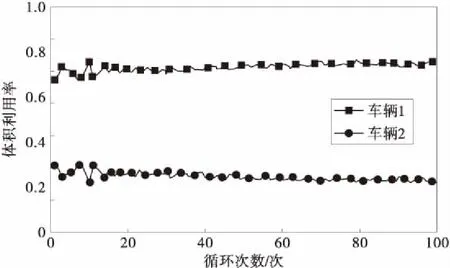
图2 体积利用率Fig.2 Volume utilization rate

对于车辆1，从图2的计算结果可以看出第10,69,79,99次循环时的装箱结果最好且相同，其装箱数量为40，体积利用率为0.758 1，重量利用率为0.742 5，得到的第99次循环的最优装箱如表3。

表3 最优装箱单Table 3 The optimum packing list

将文中方法求得的装箱结果和使用满足2.2节中的装箱约束条件的贪心算法,按货物体积大小进行装箱的结果，以及不使用初始解的蚁群算法进行比较，结果如表4。

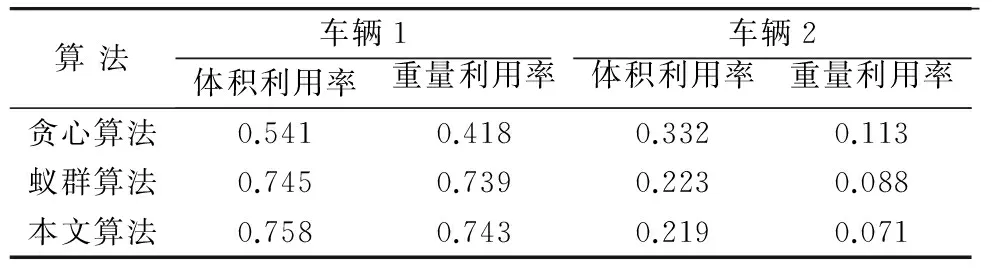
表4 装箱结果比较Table 4 The comparison of packing results

从表4可以看出，文中算法在车辆1的体积利用率和重量利用率都是高于贪心算法的，说明文中算法是合理有效的。文中算法和不使用初始解的蚁群算法在结果上相差不多，但是在计算时间上，通过100次循环，文中算法用时43.1s，而不使用初始解的蚁群算法用时51.4s，文中算法在执行效率上明显优于不使用初始解的蚁群算法。

5 结 论

货车装箱问题是不同于集装箱装箱的多约束的三维装箱问题，其需要多点卸货的需求是以往集装箱装箱所不需要考虑的。笔者基于此建立了基于体积利用率、重量利用率和装卸距离的数学模型，并根据实际需要定义了货物装卸的相关约束。在求解方法上通过求得初始可行解作为蚁群算法的初始解，在最大最小蚁群算法的基础上设计了相应的求解算法以求得最优的装货顺序。并通过实例验证了笔者提出的模型和算法对解决有多点卸货需求的货车装箱问题是有效可行的，今后的研究将进一步围绕如何细化各类装箱约束和优化装箱方法继续进行。

[1] JOHNSON D S.计算机和难解性-NP完全性理论导论[M].张立昂,译.北京:科学出版社,1990:124-125. JOHNSON D S.ComputerandIntractability-NPCompleteTheoryIntroduction[M].ZHANG Li’ang,Translate.Beijing:Science Press,1990:124-125.

[2] DOWSLAND K A,DOWSLAND W B.Packing problems[J].EuropeanJournalofOperationalReasearch,1992,56(1):2-14.

[3] ORTMANN F G,NTENE N,VAN VUUREN J H.New and improved level heuristics for the rectangular strip packing and variable-sized bin-packing problems[J].EuropeanJournalofOperationalResearch,2010,203(2):306-315.

[4] CRAINIC T G,PERBOLI G,TADEI R.“TS2PACK”:a two-level tabu search for the three-dimensional bin packing problem[J].EuropeanJournalofOperationalResearch,2009,195(3):744-760.

[5] LARA O D,LABRADOR M A.A multi-objective ant colony-based optimization algorithm for the bin packing problem with load balancing[C]// 2010IEEECongressonEvolutionaryComputation(CEC).IEEE,2010:1-8.

[6] 张德富,彭煜,朱文兴,等.求解三维装箱问题的混合模拟退火算法[J].计算机学报,2009,32(11):2147-2156. ZHANG Defu,PENG Yu,ZHU Wenxing,et al.A hybrid simulated annealing algorithm for the three-dimensional packing problem[J].ChineseJournalofComputers,2009,32(11):2147-2156.

[7] HUANG Wenqi,HE Kun.A caving degree approach for the single container loading problem[J].EuropeanJournalofOperationalresearch,2009,196(1):93-101.

[8] 卫家骏.一种集装箱船配载问题改进算法探讨[J].重庆交通大学学报(自然科学版),2009,28(5):969-972. WEI Jiajun,.A revised algorithm to solve container ships stowage problem[J].JournalofChongqingJiaotongUniversity(NaturalScience),2009,28(5):969-972.

[9] 连志刚,林蔚天,曹宇,等.基于类粒子群算法的集装箱装载模型优化研究[J].重庆交通大学学报(自然科学版),2014,33(2):126-130. LIAN Zhigang,LIN Weitian,CAO Yu,et al.Similar particle swarm optimization algorithm for the optimization of container loading model[J].JournalofChongqingJiaotongUniversity(NaturalScience),2014,33(2):126-130.

[10] 曹玲芝.求解三维装箱问题的混合模拟退火算法研究[D].广州:华南理工大学,2013:23-40. CAO Lingzhi.StudiesonHybridSimulatedAnnealingAlgorithmforThree-dimensionalBinPackingProblems[D].Guangzhou:South China University of Technology,2013:23-40.

[11] 靳志宏,于波,侯丽晓.厢式货车配载与配送的联合优化[J].交通运输工程学报,2010,10(3):95-100. JIN Zhihong,YU Bo,HOU Lixiao.Integrated optimization on both vehicle filling and routing for van truck transportation[J].JournalofTrafficandTransportationEngineering,2010,10(3):95-100.

[12] LAYEB A,BOUSSALIA S R.A novel greedy quantum inspired cuckoo search algorithm for variable sized bin packing problem[J].InternationalJournalofMathematicsinOperationalResearch,2014,6(6):732-751.

[13] DORIGO M,BIRATTARI M.AntColonyOptimizationEncyclopediaofMachineLearning[M].U.S:Springer,2010:215-216.

[14] NING Xin,KA-CHI L,CHUN-KIT L M.Dynamic construction site layout planning using max-min ant system[J].AutomationinConstruction,2010,19(1):55-65.

Multi-Unloading Packing Problem Model Research Based on MMAS

TIAN Ran, SUN Linfu, TANG Huijia, LI Binyong

(College of Information Engineering and Technology, Southwest Jiaotong University, Chengdu 610031, Sichuan, P. R. China)

Aiming at the packing problems of container truck with multiple loading points, goods variety and multi-truck carriers, cargo loading and unloading sequence for different unloading locations was generated. Mathematical model was set up based on volume, weight and loading-unloading distance and the constraints to various packing types were defined. Firstly, a feasible solution generated as per packing rule and packing constraint served as initial solution by ant colony algorithm. Then, pheromone and selection probability formula was defined in accordance with characteristics of ants route seeking on goods to calculate the optimum solution within certain cycle numbers by max-min ant colony algorithm so as to achieve the goal of maximum loading utilization and maximum volume utilization of goods truck. Finally, the rationality and effectiveness of this method is justified by a practical case.

traffic engineering; multi-unloading point; vehicle loading; max-min ant colony algorithm

10.3969/j.issn.1674-0696.2016.02.32

2014-08-11；

2015-01-22

四川省科技支撑计划项目(2014GZ0142)；汽车及工程机械多产业链业务协同服务平台研发(2013AA040606)

田 冉(1981—)，男，河南南阳人，博士研究生，主要从事物联网、数据挖掘等方面的研究。E-mail:troom@163.com。

U492.3+12; TP301

A

1674-0696(2016)02-156-07