基于计算流体动力模型的沥青胶浆流变特性模拟
齐 玉 清
(内蒙古建筑职业技术学院 建筑工程学院,内蒙古 呼和浩特 010070)
基于计算流体动力模型的沥青胶浆流变特性模拟
齐 玉 清
(内蒙古建筑职业技术学院 建筑工程学院,内蒙古 呼和浩特 010070)
采用计算流体动力模型,对旋转黏度仪进行了数值模拟。利用数值技术和复杂的流变模式,将沥青胶浆中假塑性和触变性等不同的效应予以区隔。除此之外,填缝料颗粒移动的效应也予以界定和模型化。研究显示:使用适当的计算流体动力模型能够量化和模拟上述这些重要的效应,且旋转黏度仪所使用的传统稳态流黏度方程式并不能适用于含有填缝料的沥青胶浆。
道路工程;流变行为;沥青胶浆;计算流体动力模型
0 引 言
沥青中添加填缝料的两个主要目的在于能改善沥青混凝土的力学性质,并且能有效使用废料以达环保减废的益处。填缝料与沥青之间经过物理化学作用形成沥青胶浆,其影响层面涵盖配合设计、铺筑和路面性能。沥青胶浆影响着粒料颗粒的浸润作用,也因此影响沥青混凝土的粒料间空隙(VMA)、压实特性以及最佳沥青含量等。在运送和铺筑期间,沥青胶浆必须具有足够的劲度以避免发生沥青渗流的现象。这尤其对开级配或间断级配而言,诸如开级配磨耗层(OGFC)、SMA和排水路面等,甚为重要。长期以来普遍认为沥青胶浆会影响沥青混凝土的路面性能[1-2]。
对于路面材料工程师而言,沥青和沥青胶浆,即沥青-填缝料系统的高温流变性质是一重要的工程性质。路面材料工程师需要了解填缝料对沥青黏度的影响,并确保填缝料颗粒能均匀分散于其间。沥青胶浆的高温流变性质是决定沥青混凝土最佳拌合温度的关键。而更为重要的是沥青胶浆的高温流变性质可能作为路面性能的预测指标。因此在量测流变性质时,试验的准确性和再现性就变得极为重要。目前工程界普遍使用旋转黏度仪来量测沥青胶浆的高温流变性质。G.AIREY等[3]和姚立阳,欧阳君等[4-5]的研究显示,使用旋转黏度仪量测时,沥青胶浆的高温行为常呈现剪切变稀的效应。在试验期间,沥青胶浆从初始的高黏度逐渐减少,直至黏度达到与剪变率无关的平衡稳态,即牛顿流行为。在试验过程中,黏度有时甚至减少达一个数量级。
此种剪切变稀的现象是由两个常相混淆的效应,即假塑性和触变性所造成的[6-8]。假塑性流指的是流体黏度随着剪变率的增加而减少的行为;而触变性流则指的是在连续剪力作用下,流体黏度随着时间增加而减少的行为。这两个效应常因并存于流体中而难以区分。除了剪切变稀的现象,路面材料工程师也关心旋转黏度仪所使用的传统稳态流黏度方程式是否依然能适用于含有高比例填缝料的沥青胶浆系统。
为解决上述两个问题,笔者利用计算流体力学模型,对旋转黏度仪进行数值模拟。借助数值技术和复杂的流变模式,将沥青胶浆中假塑性和触变性等不同的效应予以区隔,并且考虑含有不同比例的填缝料时对沥青胶浆高温流变行为所造成的影响。最后笔者将比较试验与模拟的结果加以验证与分析。
1 研究方法
笔者的研究中所有试验均使用Brookfield旋转黏度仪进行实际量测。旋转黏度仪的基本原理是量测旋转锤于沥青试样中维持一特定旋转速率或剪变率下所需的扭矩。图1为旋转黏度仪试验槽和旋转锤的示意。

图1 旋转黏度仪的示意Fig.1 Schematic diagram of rotational viscometer
如果试验槽和旋转锤的尺寸已知,假设试验槽和旋转锤间距间各点的剪变率相同,则试样的黏度可由扭矩和剪变率计算而得。研究实验的设计是着眼于造成黏度随试验时间递减的潜在原因,填缝料对沥青胶浆高温流变性质的影响,以及试验槽和旋转锤间距间黏度相同的假设是否成立。因此研究中使用90 #直馏沥青作为基质沥青,并且另行添加二种不同体积组成比例炉石粉(10%、30%)以拌制沥青胶浆,基质沥青和炉石粉的比重分别为1.05和2.70,然后在两种试验温度和不同的剪变率作用下进行试验以评估不同温度和剪变率对沥青和沥青胶浆流变行为的影响。其中剪变率的大小是依据黏度仪所能提供的极限扭矩来决定。
表1为本研究实验配置,此处填缝料采用体积比例的原因在于后续扩散理论应用的需要,利用沥青胶浆各组成材料的重量和比重,得以计算拌制试验所相应的体积比例。

表1 实验配置
在数值模拟的部分,使用计算流体动力商业软件FLUENT[9]。计算流体动力学(简称CFD)是流体力学领域的重要技术之一,使用数值方法在电脑中对流体动力学的控制方程进行求解,从而可预测流场的流动。CFD最基本的考虑是如何把连续流体在电脑上用离散的方式处理。方法之一是把空间区域离散化以形成一个立体网格,然后基于对流动黏滞流体的质量和动量守恒的假设以求解Navier-Stokes运动方程组[10]。质量守恒可由下列微分方程所描述:
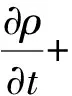
(1)
式中:ρ为流体密度,g/cm3;v为流体速度,cm/s;t为时间,s。
同样地,动量守恒可由微分方程式(2)描述:
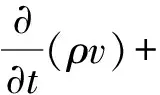
(2)
(3)

式(1)、式(2)均采用卡氏坐标。
由于旋转黏度仪为一轴对称系统,因此使用适当的方法我们能将模型从三维简化为二维轴对称的旋转系统。式(1)、式(2)的简化形式和细节可参考FLUENT使用手册[9]。式(3)右边第2项代表流体的体积膨胀,在本研究中可以忽略不计。因此对于不可压缩的牛顿流体,剪应力与变形张量率D呈正比。变形张量率D,即式(3)等式右边第1项,如式(4):
D=▽v+▽vT
(4)
剪变率被定义为变形张量率的第二不变量:
(5)
对于牛顿流体,剪应力和剪变率的关系即可表示为常见的型式,如式(6):
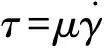
(6)
过去使用旋转黏度仪量测的经验显示,沥青胶浆的高温行为常存在非牛顿流的行为,因此上述模型需要进一步的修正。
首先假设沥青初始的高黏度是因为触变性所造成的。基于M.MODIGELL等[11]的研究成果,笔者使用FLUENT的使用者自订函数(UDFs)增加一触变性模型。虽然Modigell和Koke的研究是针对半固体合金的流变行为,但仍适用于本研究所探讨的情况。笔者尝试导入一个结构参数κ来描述沥青内部的结构特性。此结构参数的动力特征可以如式(7)的一阶反应式来表示。
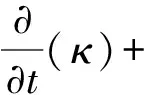
(7)
式中:C为反应速率,1/s,并假设为一常数;κe为已知剪变率下结构参数的平衡当量值。
为计算沥青的假塑性行为,黏度使用幂次方模式,即:
(8)
式中:k为稠度指标;n为决定流体行为的材料参数,n=1为流体为牛顿流,n<1为一假塑性流体。
在整个模拟过程中,结构参数从初始值κ0逐渐减小至平衡当量值κe。平衡当量值κe通常视为一剪变率的函数,如式(9):
(9)
其中:考虑使用旋转黏度仪量测沥青黏度,当达到平衡状态时,最终稳态黏度与剪变率无关;因此,m=(1-n)。
由过往经验与本研究试验结果可知,沥青-填缝料胶浆明显拥有较高的黏度和较长的递减时间,上述模式由于并未考虑填缝料的影响,因此可能无法适切地描述沥青-填缝料胶浆系统。依据D.LEIGHTON等所提出的由剪力引起的扩散理论[12-14],得以描述固体悬浮粒在流体中颗粒局部集中的变化情形。
扩散过程包含两种作用:第一种作用是颗粒因为彼此经历较多的碰撞而自高度集中区域扩散开来,此外颗粒将从高剪力区域向低剪力区域移动。这两种效应能如式(10)。
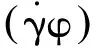
(10)
式中:Kc为一常数;d为颗粒平均直径,μm;φ为颗粒的体积组成比例。
第二种作用是颗粒将从高黏度区域向低黏度区域移动:

(11)
式中:Kη为一常数;η为黏度,Pa·s。
颗粒体积组成比例的传播方程式,如式(12):
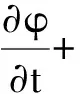
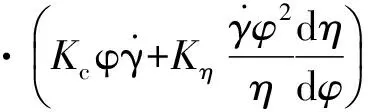
(12)
考虑颗粒的影响,式(8)将修正为式(13):
(13)
其中:若仅模拟纯沥青的情况,则φ,B,Kc,Kη,d均为0。
2 试验和模拟结果
CFD模拟须要建立网格,本研究采用以旋转锤中心为轴的二维轴对称型式,如图2。内部、外部和底部边界均为束制边界,其中内部边界面乃为与旋转锤的接触面,所以设定施加一角速度以呈现试验状况下以固定剪变率旋转锤的旋转。
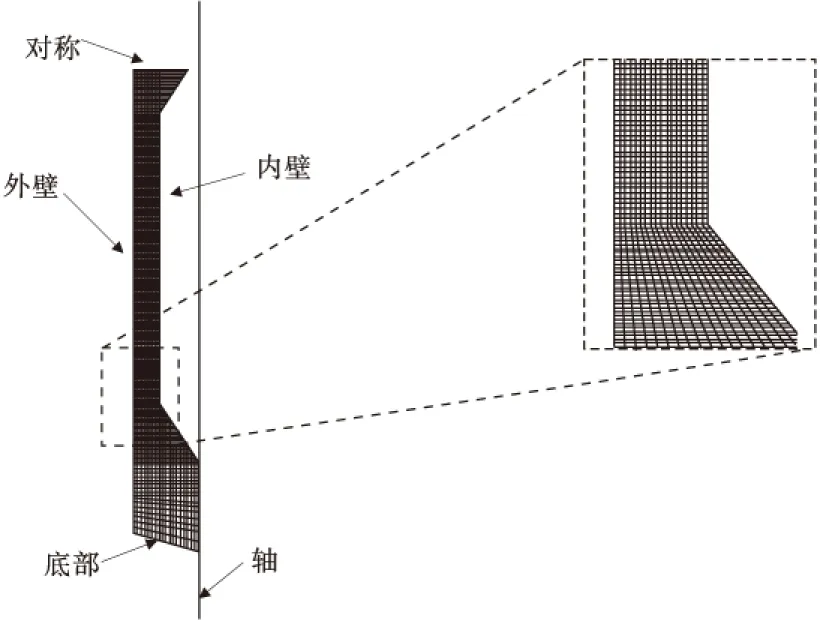
图2 二维轴对称网格Fig.2 Two-dimensional axis symmetric grid
CFD模拟所使用的各项参数,如表2。式(9)中当达到平衡状态时黏度与剪变率无关,纯沥青的最终稳态黏度可求得m,n。然后经由已知的m,n和式(8)可得与剪变率无关的初始值κ0。至于常数B,Kc,Kη也可由沥青-填缝料胶浆的黏度数据而得。
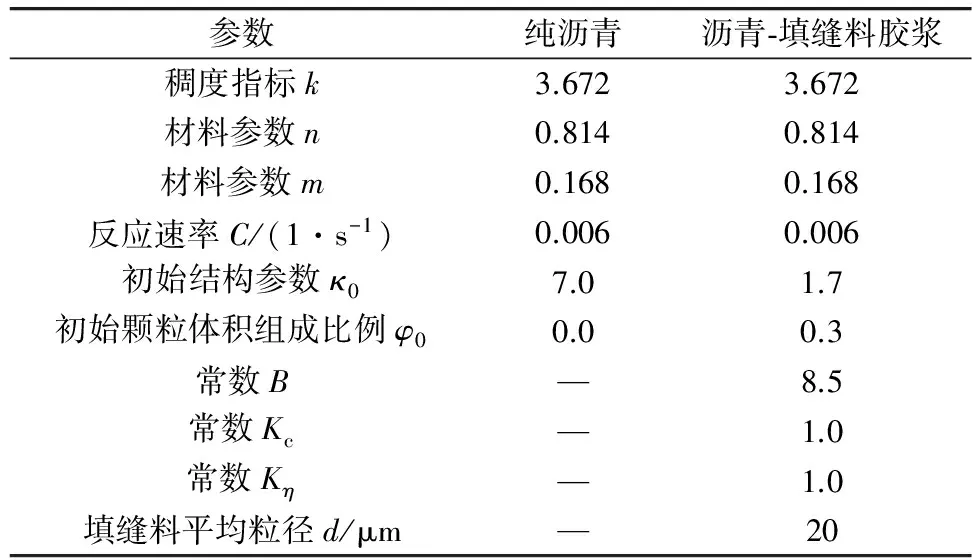
表2 CFD模拟使用的各项参数
图3分别为Brookfield旋转黏度仪于100,150 ℃的试验结果。值得注意的是,无论是纯沥青或沥青-填缝料的沥青胶浆均显示出黏度随时间渐减的结果。此外纯沥青在低剪变率作用下(ssr=1.36s-1),其黏度渐减的程度大于在高剪变率的作用(ssr=6.80s-1)。在低剪变率作用下纯沥青的初始黏度也大于高剪变率作用者,不过两者的黏度均于约15 min后达到稳定。比较相同剪变率作用下(ssr=1.36s-1),纯沥青和沥青-填缝料胶浆可知,纯沥青的黏度随时间减少的比例大于沥青-填缝料胶浆,且达稳定后沥青-填缝料胶浆的黏度约为纯沥青黏度的12倍。这些现象都显示填缝料明显提供沥青的加劲效果。
由图3(a)中纯沥青的黏度所得,在不同剪变率作用下,以CFD模型模拟20 min的结果和实验结果相当一致。相比之下,CFD模拟沥青-填缝料胶浆黏度渐减的效果就明显不如预测纯沥青者,但是CFD模型仍然能掌握沥青胶浆剪切变稀的流变行为。
图3(b)与图3(a)比较,纯沥青或沥青-填缝料的沥青胶浆在试验温度150 ℃下黏度随时间渐减的比例均大于试验温度100 ℃的试验结果。此外与试验温度100 ℃的试验结果相异之处是,在不同的剪变率作用下,沥青黏度随时间渐减的程度并无明显的差异。这意味着沥青的假塑性行为似与温度相关,较高的试验温度将减少假塑性对沥青黏度渐减的影响。而和图3相同的是,纯沥青的黏度约在15 min后达到稳定,但沥青-填缝料胶浆的黏度则在15 min后仍持续缓慢减少,至试验结束时仍未达稳定,这也显示传统的稳态流黏度方程式并不能适用于含有填缝料的沥青胶浆系统。

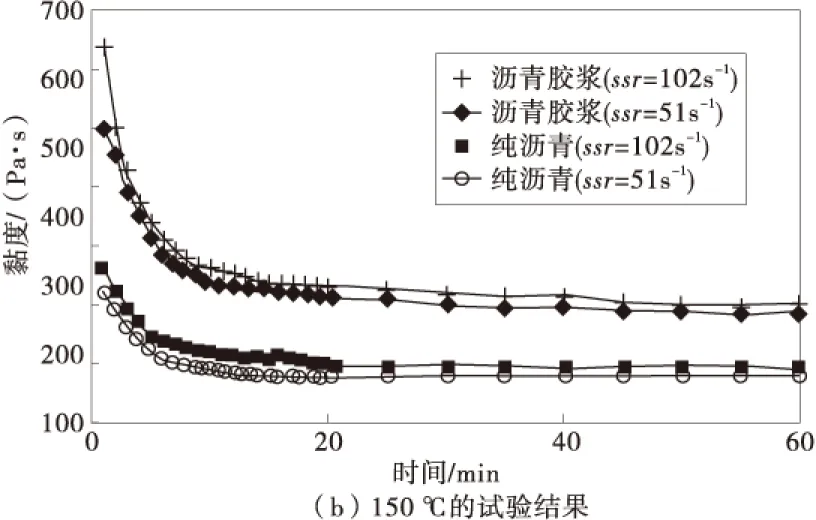
图3 Brookfield旋转黏度仪的试验结果Fig.3 Test results of Brookfield rotational viscometer
图4和图5为在试验温度100 ℃下,旋转黏度仪试验槽内沥青胶浆的CFD模拟结果。其中内部边界面乃为与旋转锤的接触面,外部边界面则是指试验样品槽的边缘壁面,如图2。对照图4和图5可知,填缝料的颗粒移动对于黏度仪内部至外部边界的黏度变异具有显著的影响。对于沥青-填缝料胶浆,如图4,黏度仪内的黏度并非为一定值,所谓固定的黏度仅是一项假设。同样的,也能从图5观察到颗粒的体积组成比例φ自试验槽内部至外部边界逐渐提高,即填缝料颗粒在受剪作用下向外部移动。这也说明了图3中沥青-填缝料胶浆在前10 min初始黏度的快速减少是由于沥青流体的触变性所造成的,而后黏度的持续减少主要是来自于沥青内填缝料的移动,此时触变性效应已不再发挥明显的作用。
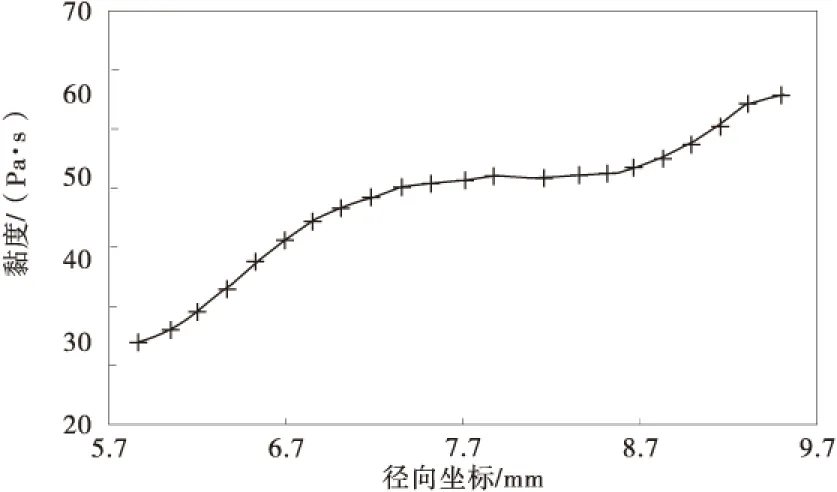
图4 黏度仪内部至外部边界的黏度变异Fig.4 Viscosity variation at internal and external boundary of viscometer

图5 黏度仪内部至外部边界颗粒的体积组成比例的变异Fig.5 Variation of particle size composition at internal and external boundary of viscometer
3 结 论
1)笔者使用CFD模型对旋转黏度仪进行数值模拟。将沥青胶浆中假塑性和触变性等不同的效应予以区隔,并且考虑含有不同比例的填缝料时对沥青胶浆高温流变行为所造成的影响。经由试验结果验证CFD模型可知,此模型能量化这些效应,并掌握一些重要的特性。此模型的另一优点在于选择适当的填缝料、填缝料的添加量等方面能大量简化相关试验。
2)研究结果显示沥青在旋转黏度仪中的高温流变行为本身极为复杂,尤其是添加填缝料后更是如此。借由CFD模型可知,纯沥青具有剪切变稀的行为,此行为乃是由假塑性和触变性的联合效应所造成的,而当达到稳态状态时,即呈现牛顿流行为。在未达到稳态流之前,由于二种效应的参与,将不易预测沥青的暂态黏度。但整体而言,在不同剪变率作用下,CFD模拟纯沥青的黏度和实验结果相当一致。一旦添加填缝料,颗粒的存在会干扰沥青原有的流变行为,沥青-填缝料胶浆的黏度持续缓慢减少,至试验结束时仍未达稳定,这也显示传统的稳态流黏度方程式并不能适用于含有填缝料的沥青胶浆系统。虽然CFD模拟沥青-填缝料胶浆黏度渐减的效果明显不如预测纯沥青,但是CFD模型仍然能掌握沥青胶浆流变行为中剪切变稀的特性。沥青胶浆中填缝料颗粒的移动明显长时间持续影响沥青黏度的渐减,且颗粒移动对于黏度仪内部至外部边界的黏度变异也具有显著的影响。对照实际试验结果可知,使用适当的CFD模型能够量化和模拟这些效应。比较两种不同温度的试验结果可知,试验温度150 ℃时在不同的剪变率作用下,沥青黏度随时间渐减的程度并无明显的差异。这显示沥青的假塑性行为似与温度相关,较高的试验温度将减少假塑性对沥青黏度渐减的影响。
[1] BUTTLAR W,BOZKURT D,AL-KHATEEB G,et al.Understanding asphalt mastic behavior through micromechanics [J].TransportationResearchRecord:JournaloftheTransportationResearchBoard,2013,1681:157-166.
[2] CRAUS J,ISHAI I,SIDES A.Some physio-chemical aspect of the effect and the role of the filler in bituminous paving mixtures [C]// Proceeding in Association of Asphalt Paving Technologists,2010,45:558-588.
[3] AIREY G,WESTWOOD D.High temperature viscosity of polymer and filler modified binder systems [C]// Proceedings of the 3rdEurasphalt and Eurobitume Congress,2004,2:1599-1608.
[4] 姚立阳,姚丽红,马勤.纤维沥青胶浆动态剪切流变参数与温度相关性研究[J].重庆交通大学学报(自然科学版),2012,31 (4):781-784. YAO Liyang,YAO Lihong,MA Qin.Relevance of dynamic shear rheometry parameter of fiber asphalt binder and temperature [J].JournalofChongqingJiaotongUniversity(NaturalScience),2012,31 (4):781-784.
[5] 欧阳君,孙大权,章毅.基于流变性能的SBS改性沥青老化动力性能研究[J].重庆交通大学学报(自然科学版),2011,30(3):411-414. OUYANG Jun,SUN Daquan,ZHANG Yi.Investigation of aging kinetics of SBS modified asphalt based on rheological properties [J].JournalofChongqingJiaotongUniversity(NaturalScience),2011,30(3):411-414.
[6] Saric-Coric M,Liotta F,Khayat K H.Influence of thixotropy on stability characteristics of cement grout and concrete [J].ACIMaterialsJournal,2011,99 (3):234-241.
[7] 王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004. WANG Fujun.ComputationalFluidDynamicsAnalysis:TheoryandApplicationofCFDSoftware[M].Beijing:Tsinghua University Press,2004.
[8] 张延芳.计算流体力学[M].大连:大连理工大学出版社,2007. ZHANG Yanfang.ComputationalFluidMechanics[M].Dalian:Dalian University of Technology Press,2007.
[9] Fluent Inc.FluentUser’sGuide[M].U.S.:Fluent Inc.,2003.
[10] FERZIGER J,PERIC M.ComputationalMethodsforFluidDynamics[M].3rded.Berlin:Springe-Verlag,2002.
[11] MODIGELL M,KOKE J.Time-dependent rheological properties of semi-solid metal alloys [J].MechanicsofTime-DependentMaterials,2008,3(1):15-30.
[12] LEIGHTON D,ACRIVOS A.The shear-induced migration of particles in concentrated suspensions [J].JournaloftheFluidMechanics,2007,181:415-439.
[13] WALLEVIK J E.Thixotropic investigation on cement paste:experimental and numerical approach [J].JournalofNon-NewtonianFluidMechanics,2005,132(1/2/3):86-99.
[14] 田美霞.考虑浆液黏度时变性的单裂隙动水注浆扩散模型[J].重庆交通大学学报(自然科学版),2011,30(增刊1):536-537. TIAN Meixia.A model for grouting into single fracture with flowing water based on time-dependent behavior of viscosity [J].JournalofChongqingJiaotongUniversity(NaturalScience),2011,30(Sup1):536-537.
Rheological Properties Simulation of Asphalt Mastic Based onComputational Fluid Dynamics Model
QI Yuqing
(School of Architecture Engineering, Inner Mongolia Technical College of Construction, Hohhot 010070, Inner Mongolia, P.R.China)
The numerical simulation of the rotational viscometer was carried out by Computational Fluid Dynamics (CFD) model. By means of numerical techniques and complex rheological models, the pseudo-plastic and thixotropic nature of the asphalt binder was identified and insulated. In addition, the effect of filler drift was identified and modeled. The research indicates that the appropriate CFD model can quantify and simulate the above important effects, and the traditional steady state equations used to calculate viscosity in the viscometer are not applicable for asphalt-filler mastic.
highway engineering; rheological behavior; asphalt mastic; computational fluid dynamic model
2014-12-02;
2015-03-12
齐玉清(1971—),女,内蒙古呼和浩特人,副教授,主要从事力学与结构方面的研究。E-mail: qiyuqing888@126.com。
10.3969/j.issn.1674-0696.2016.01.11
U414
A
1674-0696(2016)01-056-04

