基于IEEMD和ARMA算法的斜拉桥模态参数识别

袁 泉，何 杰

(1.贵州省公路局，贵州 贵阳 550003；2.西南交通大学 建筑与土木工程学院，四川 成都 610031)

基于IEEMD和ARMA算法的斜拉桥模态参数识别

袁 泉1，何 杰2

(1.贵州省公路局，贵州 贵阳 550003；2.西南交通大学 建筑与土木工程学院，四川 成都 610031)

提出了一种基于IEEMD分解的ARMA改进识别算法。首先对实测加速度信号进行IEEMD分析，之后利用聚类分析检验所得的本征模态函数(IMFs)中是否存在模态混叠；然后采用模糊综合评价法计算每个IMF与实测信号之间的模糊相似系数，以便选出有效的IMF分量；再利用主成分分析和帕累托图法对保留下来的IMFs进行信号的重构，进而达到对实测信号的有效分解和降噪效果；最后将重构的动力信号作为ARMA算法的输入，进行模态参数识别。通过对比分析每阶频率与实际值的误差百分比，可知利用IEEMD处理之后的振动信号作为ARMA算法的输入能得到与真实值最为接近频率值，且误差的百分比都在3%以下，验证了该识别方法能有效的识别到斜拉桥的频率。

桥梁工程；IEEMD；模糊综合评价法；主成分分析；帕累托图；ARMA

0 引 言

随着桥梁结构使用年限的增加，其功能会逐渐下降，所以需要对桥梁结构进行定期的可靠性评估[1]，以便更好掌握桥梁结构自身的健康状况，确保其正常运行。实际应用中，结构可靠性可通过分析其模态参数来实现。现阶段，桥梁结构模态参数的识别[2]可以通过利用某些措施使桥梁结构产生一定的振动，并采集结构自身的振动信号，再利用相关数学软件得出具体的频响函数(频域)或脉冲相应函数(时域)，达到识别桥梁的结构模态参数。上述方法被广泛运用于识别一些小型桥梁的模态参数，但对于大型的桥梁而言，比如：斜拉桥、悬索桥等，则需要利用更为精确的识别方法。现阶段，国内外都在研究一种新的参数识别方法[3-4]，即：基于环境振动的结构模态参数识别方法。笔者研究的主要内容包括两个方面：①对现有的集合经验模态分解(Ensemble Empirical Mode Decomposition, EEMD)进行提高得到提高的集合经验模态分解(Improve Ensemble Empirical Mode Decomposition, IEEMD)，利用改进之后的IEEMD对振动信号进行预处理和信号重构；②将重构的信号作为输入，利用ARMA算法[5]进行模态参数识别，并检验笔者提出方法的可行性。

1 集合经验模态分解(EEMD)

集合经验模态分解[6](EEMD)实质上是一种噪声辅助数据分析方法，EEMD分解具体步骤如下：

1)原始信号x(t)中加入N个不同的 Gaussian 白噪声wi(t)(i=1,2,…,N)，即

xi(t)=x(t)+wi(t)

(1)

式中：xi(t)为第i次加入白噪声后的信号；wi(t)为第i次加入白噪声。

2)对加入了白噪声的信号xi(t)分别进行EMD分解，得到相应的IMFij和一个余项rij，其中IMFij(j=1,2…,n)表示第i次加入白噪声后分解所得的第j个IMF，即：

(2)

式中：n表示每次EMD分解得到的IMF和r的总的个数。

3)利用不相关随机序列的统计均值为0的原理，将上述对应的IMF进行总体平均运算，得到EEMD分解后最终的IMF，即：

(3)

式中：IMFj为对原始信号进行EEMD分解后所得的第j个IMF。

EEMD虽然是在EMD基础上改进得到的一种分解方法，但其依然存在以下几方面的缺陷：①需要人工定义白噪声的幅值标准差，且加入的幅值标准差没有一定的规范标准；②加入白噪声的次数，即在EEMD法中的集成次数同样需要人工对其进行定义；③不能事先确定输入信号与IMFs的相对误差；④不能判定得到的本征模态函数(IMFs)之间是否存在模态混叠现象；⑤不能实现IMF的有效选取；⑥不能实现信号的自我重构。

2 集合经验模态分解(EEMD)的改进

针对EEMD法中存在的缺陷，提出了IEEMD法，IEEMD具体的流程见图1。以下就如何实现集合经验模态分解的改进进行详细的分析。

图1 IEEMD基本流程Fig.1 Flowchart of IEEMD

2.1 白噪声的选择

在利用EEMD进行模态分解时，加入白噪声的幅值标准差不同，则得到的分解结果也就不同，所以有必要根据振动信号自身的特点来确定加入白噪声的幅值标准差。加入的白噪声应该满足如下两个条件[7]：①白噪声的加入不会影响原始信号中高频成分极值点分布情况；②能改变信号中低频成分的极值点间隔分布，使间隔减小且分布均匀，以便减小在使用三次样条函数进行拟合包络时，求解局部均值的误差。考虑到加入白噪声的幅值标准差不能太低也不能过高，过低则不能满足条件1，过高则不能满足条件2。以下就如何选择白噪声进行分析。

Step1:根据原始信号计算其幅值标准差σ0；

Step2:对原始信号进行高通滤波分解，得到一个高频分量和一个低频分量，并计算高频分量的幅值标准差为σh;

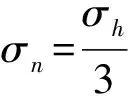
2.2 IEEMD方法中集成次数的确定

加入白噪声的幅值比值系数与集成次数之间存在如下的关系[7]:

(4)

式中：e为输入信号与IMFs的相对误差；σn为加入的白噪声幅值标准差；σ0为原始信号幅值标准差；M为在EEMD方法中集成的次数。

当加入白噪声的幅值标准差和输入信号与IMFS的相对误差e被确定时，便能根据式(4)推算出具体的集成的次数。

2.3 聚类分析

利用欧式距离对所有的IMFs进行聚类分析[8]，以便检验IMFs之间是否存在模态混叠。

2.4 有效IMF的选取

利用模糊综合评价法[9]对所有的IMFs进行判别分析，对于每个IMF都能计算出系统的频率f，阻尼比ξ和振型m，所以选择这3个参数作为评价因子。IMF与原始信号之间的模糊相似系数ri可由式(5)计算。

(5)

式中：ri为第i个IMF与原始信号之间的模糊相似系数；wf,wξ,wm分别为频率f，阻尼比ξ和振型m的权重[10]；f，ξ，m分别为原始信号的频率，阻尼比和振型；fi，ξi，mi分别为第i个IMF的频率，阻尼比和振型。

在实际应用中，频率和振型会随着计算阶次的升高而逐渐稳定，而阻尼一般会发生较大波动，所以文中阻尼比的权重相对较小，式(5)中wf=0.5，wξ=0.2，wm=0.3。ri越接近1则表示该第个IMF分量与原始信号的相识程度越高，当ri>0.3时[10]，则认为该IMF为有效IMF。

2.5 主成分分析与帕累托图

主成分分析[11]的基本思想是：利用线性变换对多个变量进行重新组建，以选出较少个数的重要变量，其实质是一种多元统计分析方法。利用主成分分析分析有效的IMFs，再运用帕累托图计算每一主成分对方差的贡献量，保留累积方差贡献率达到90%的IMF分量，最后对保留下来的IMF分量进行信号的重构，即：

(6)

式中：x(t)为重构的信号；k为保留下来的IMF的个数。

3 ARMA模型时间序列分析法

ARMA模型时间序列分析法[12]的基本思路为：

1)实际应用中可以利用高阶微分方程来描述N个自由度的线性系统激励与响应之间的关系。对于离散时间域而言，该高阶微分方程便是由一系列不同时间段的时间序列构成的差分方程，即ARMA时序模型方程，如式(7)，该式能够用于表示xt(响应数据序列)与xt-k(历史值)之间的具体关系。

(7)

式中：等式的左边为AR模型，即自回归差分多项式；等式的右边为MA模型，即滑动平均差分多项式；2N为自回归和滑动均值模型的阶次；ak为待识别系统的自回归系数；bk为待识别的滑动均值系数；ft为白噪声激励。需要注意的是：当k=0时，将a0、b0视为1。

2)根据推广的Yule-walker方程式(8)，并采用伪逆法便可求该方程组的最小二乘解式(9)，由此求得自回归系数ak(k=1,2…,2N)：

(8)

(9)

式中：R为xt的自相关函数。

3)利用非线性方程组式(10)来求解滑动平均模型系数bk(1,2…,2N)：

(10)

式中：ck为响应序列xt的自协方差函数。

4)由式(9)，式(10)可求得ak和bk，便可以通过ARMA模型传递函数的表达式计算系数的模态参数，ARMA模型的传递函数如式(11)：

(11)

利用高次代数方程求解传递函数的极点，其与系统的模态频率ωk和阻尼比ξk的关系如式(12)：

(12)

5)由式(12)可求得模态频率ωk和阻尼比ξk，如式(13)：

(13)

基于IEEMD和ARMA算法的具体流程如图2。

图2 基于IEEMD和ARMA算法的流程Fig.2 Flowchart based on IEEMD and ARMA algorithm

4 某大型斜拉桥模态参数识别结果

4.1 斜拉桥实测动力信号

笔者以长江上某座大型斜拉桥为识别对象，该斜拉桥的主跨为1 088 m，桥上共布置竖向加速度传感器14个，位于主梁主跨1/6截面和次边跨1/2截面的上游和下游处，具体位置见图3。加速度信号采样频率为20 Hz，测试时间为48 h。

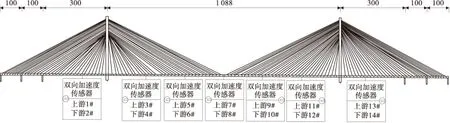
图3 传感器的布置Fig.3 Sensor layout

4.2 EEMD与IEEMD分解结果对比分析

4.2.1IMF分量对比分析

考虑到传感器采集到的加速度信号中会含有噪声，如果直接对原始信号进行模态参数识别，则识别结果与真实值的误差会较大，所以在利用ARMA算法进行模态参数识别之前，需要对加速度信号进行预处理，笔者分别运用EEMD和IEEMD对原始信号进行分解，具体结果见图4、图5。

图4 原始信号Fig.4 Original signal

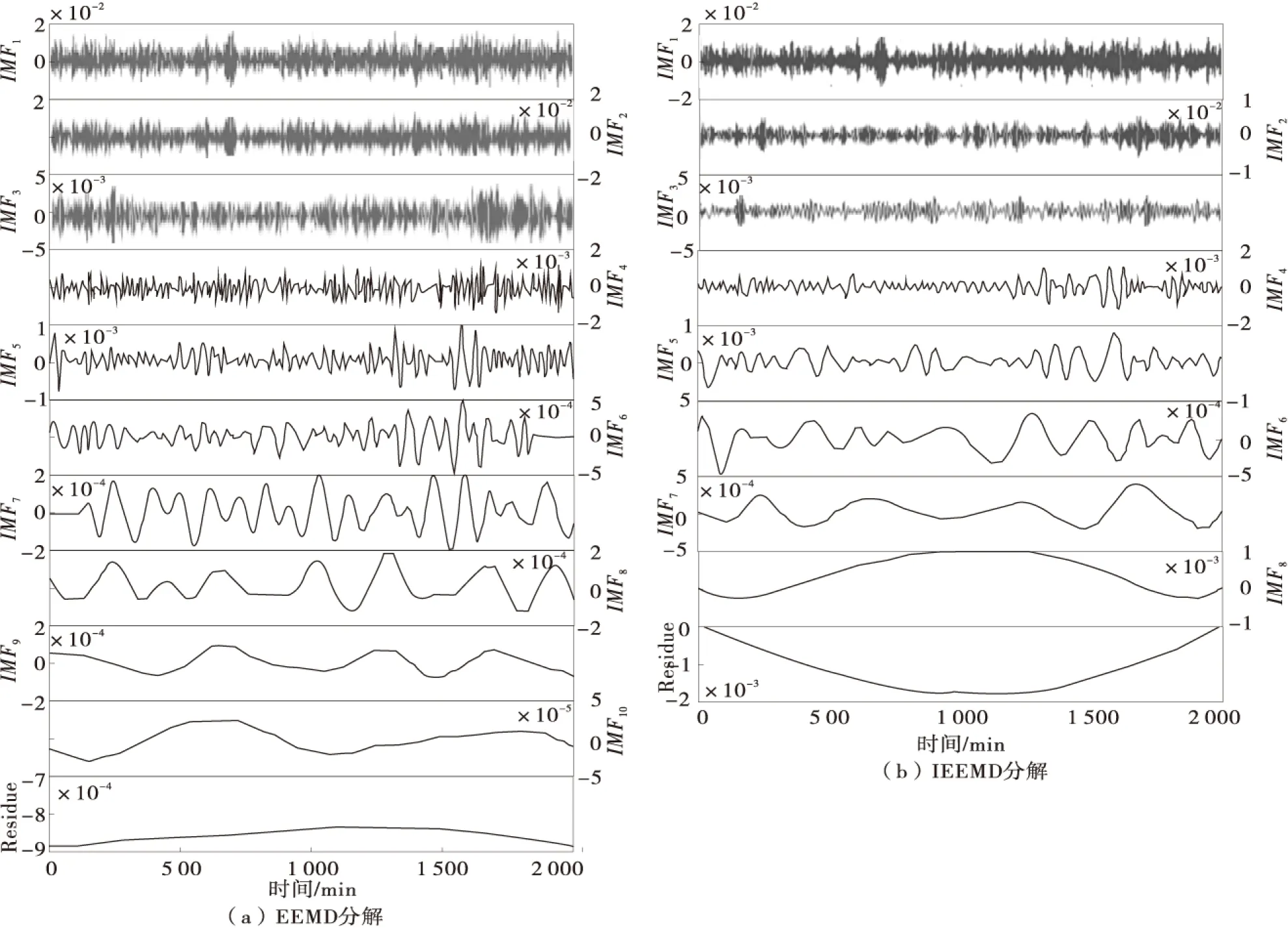
图5 EEMD及IEEMD分解Fig.5 Decomposition of EEMD and IEEMD

从图5可见，IEEMD分解之后得到了8个IMF和一个残余项，而EEMD分解之后得到了10个IMF和一个残余项。通过对比分析可得如下结论：

1)从EEMD分解结果中可知：IMF1与IMF2的频率范围都在(-0.02,0.02)，且IMF7～IMF9的频率都在(-2×10-4,2×10-4)不同的IMF中包含相同的频率成分，即存在一定的模态混叠现象。

2)IEEMD分解的结果中不存在明显的模态混叠现象。主要是因为IEEMD分解法每次分解都是将原信号的残余量作为输入，且仅取每次分解的第1阶固有模态，进而确保了模态分量的一致性，这样便能有效地避免EEMD 中不同分解过程中模态分量不一致的问题。

3)EEMD分解得到的IMFs数少于EEMD分解的结果，则间接说明了IEEMD法的计算效率较EEMD法好些。

4.2.2 聚类分析

利用欧式距离分别对EEMD分解结果和IEEMD分解结果进行聚类分析，结果如图6。

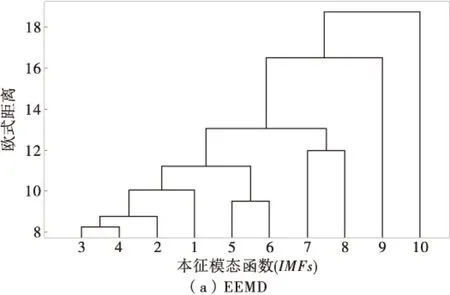
图6 EEMD和IEEMD分解结果聚类分析Fig.6 Clustering analysis of EEMD and IEEMD decomposition

从图6可知：IEEMD法分解得到的IMFs之间不存在模态混叠的现象；EEMD法分解得到的IMFs，其中IMF5与IMF6属于同一类别，IMF7与IMF8属于同一类别，原因可能是这些IMF含有相类似的信息，即存在模态混叠现象。

4.2.3 模糊综合评价结果对比

利用式(5)确定每个IMF与原始信号的模糊相似系数，具体的模糊相似系数结果见表1(只列出了IMF1-8的数据结果)。

表1 模糊相似系数对比

由表1可知：对于两种方法得到IMF1而言，由IEEMD分解得到的IMFs其模糊相似系数高于由EEMD得到的IMFs；由EEMD分解得到的IMF3和IMF4，其模糊相似系数很接近，可能的原因是这两个分量之间存在一定的模态混叠；由IEEMD分解得到的IMFs与原始信号之间的模糊相似系数是在逐渐递减的，且趋势比EEMD分解的结果更为明显，原因在于IEEMD分解法每次分解都是将原信号的残余量作为输入；IEEMD分解得到的IMFs从第5个分量开始便低于0.3，所以认为IMF5～IMF8为无效模态，保留剩下的IMF1～IMF4。

4.2.4 主成分分析与帕累托图

利用主成分分析和帕累托图分析IMF1～IMF4,计算的主成分与累积方差贡献率见图7。

图7 累积方差贡献的帕累托图Fig.7 Pareto diagram of the cumulative variance contribution

从图7可知：IMF1和IMF2的累积方差贡献率便能够达到90%,所以保留IMF1和IMF2，并利用IMF1和IMF2进行信号的重构。

4.3 ARMA算法结果

对加速度信号进行IEEMD分解之后，将重构的信号作为ARMA算法的输入，进行模态参数识别，笔者只对桥梁结构的频率进行分析，结果见图8。

从图8可见，不同阶次的频率在48 h中都存在一定的波动现象，但总体上还是保持着十分稳定的状态。

对前6阶频率数据的最大值、最小值、平均值以及平均值与真实值之间的差值百分比进行对比分析，具体数据见表2。

表2 前6阶频率数据对比分析

注：1.表中真实值来源于文献[6]；2.最大值和最小值为基于IEEMD和ARMA算法求得结果最值；3.平均值1为未对原始信号进行任何预处理，计算得到的频率值；4.平均值2(EEMD)为基于EEMD和ARMA算法求得结果的平均值；5.平均值3(IEEMD)为基于IEEMD和ARMA算法求得结果的平均值。

图8 前6阶频率48 h的变化Fig.8 Changes of the frequency of the first six orders within 48 hours

真实值与平均值1～平均值3之间的误差百分比见图9。

图9 前6阶频率与真实值的误差百分比Fig.9 Error percentage between frequency of the first six orders and actual value

在利用ARMA算法进行模态参数识别之前，对原始信号分别进行了EEMD和IEEMD分解，通过对比分析可得如下结论：

1)未对原始信号进行预处理时，得到的频率值与真实值之间的误差较大，这主要是因为原始信号是在环境激励下测得的，其内部包含一定的噪声，噪声的存在会直接影响识别的结果的准确性；

2)通过对比分析EEMD预处理和IEEMD预处理得到的频率值发现，经过IEEMD分解与重构后的信号能得到与真实值更为接近的结果，这也间接的证明IEEMD分解效果较EEMD分解效果更好一些；

3)通过对比分析表2中的差值百分比，不难发现，识别得到的前6阶频率中，对于第2阶的频率识别效果相比其它5阶而言误差更大，但都在可接受的范围之内。

5 结 论

笔者先将原始信号进行EEMD和IEEMD分解，再将分解的结果作为ARMA算法的输入，最后对该斜拉桥进行模态参数识别，通过上述分析可得到如下结论：

1)IEEMD分解法具有较好的计算效率和分解精度，且能够在得到更少的IMF分量的前提下，减小分解误差。

2)经过IEEMD分解与重构后的信号能得到与真实值更为接近的结果，这也间接的证明IEEMD分解效果较EEMD分解效果更好一些。

3)通过对比分析平均值与真实值的误差百分比，可见利用IEEMD能够对桥梁结构的动力测试信号进行有效的分解和降噪，并保留结构的信息。

4)利用基于IEEMD的ARMA算法对实桥测试数据进行模态参数识别，识别得到的频率值与真实值的误差百分比很小，可见笔者的方法能应用于实际桥梁的动力测试分析中。

[1] 漆景星,侯艳红.桥梁可靠性评估综述[J].浙江交通职业技术学院学报,2011,12(1):20-22. QI Jingxing,HOU Yanhong.Bridges reliability evaluation review [J].JournalofZhejiangInstituteofCommunications,2011,12(1):20-22.

[2] LIN P,ZHANG N,NI B.On-line modal parameter monitoring of bridges exploiting multi-core capacity by recursive stochastic subspace identification method [C]// American Control Conference.Piscataway,N.J.:IEEE,2008.

[3] 周晶.基于环境振动模态参数识别随机子空间方法与应用[D].兰州：兰州理工大学,2008. ZHOU Jing.StochasticSubspaceIdentificationandApplicationofStructuresUnderAmbientVibration[D].Lanzhou:Lanzhou University of Technology,2008.

[4] PEETERS B,ROECK G D.Reference-based stochastic subspace identification for output-only modal analysis [J].MechanicalSystems&SignalProcessing,1999,13(6):855-878.

[5] 黄雁勇,王沁,李裕奇.ARMA模型参数估计算法的改进[J].统计与决策,2009(16):7-9. HUANG Yanyong,WANG Qin,LI Yuqi.The improvement in estimation algorithm in ARMA model parameters [J].JournalofStatisticsandDecision,2009 (16):7-9.

[6] 郑近德,程军圣,杨宇.改进的EEMD算法及其应用研究[J].振动与冲击,2013,32(21):21-26. ZHENG Jinde,CHENG Junsheng,YANG Yu.Modified EEMD algorithm and its applications [J].JournalofVibrationandShock,2013,32(21):21-26.

[7] 蔡艳平,李艾华,徐斌,等.集成经验模态分解中加入白噪声的自适应准则[J].振动.测试与诊断,2011,31(6):709-714. CAI Yanping,LI Aihua,XU Bin,et al.Adaptive guideline of ensemble empirical mode decomposition with gauss white noise [J].JournalofVbration,Measurement&Diagnosis,2011,31(6):709-714.

[8] 唐东明.聚类分析及其应用研究[D].成都：电子科技大学,2010. TANG Dongming.StudyonCusteringAlgorithmanditsApplications[D].Chengdu:University of Electronic Science and Technology of China,2010.

[9] 许顺国,牟瑞芳,张雪梅.模糊数学综合评判法在水质评价中的应用——以成都市府河为例[J].唐山师范学院学报,2007,29(2):68-70. XU Shunguo,MU Ruifang,ZHANG Xuemei.The application of fuzzy mathematical comprehensive judgment to the evaluation of water quality:about the Fu River in Chengdu city [J].JournalofTangshanNormalUniversity,2007,29(2):68-70.

[10] 王彦威,邓海利,王永成.层次分析法在水安全评价中的应用[J].黑龙江水利科技,2007,35(3):117-119.WANG Yanwei,DENG Haili,WANG Yongcheng.The application in water safety evaluation using layer analysis [J].HeilongjiangScienceandTchnologyofWaterConservancy,2007,35(3):117-119.

[11] 谢沙沙,李素梅,王光华,等.基于主成分分析和支持向量机的人眼注视识别[J].信息技术,2014(7):163-166. XIE Shasha,LI Sumei,WANG Guanghua,et al.Recognition of eye gazing based on principle component analysis and support vector machine [J].InformationTechnology,2014(7):163-166.

[12] PAPPAS S S,EKONOMOU L,KARAMOUSANTAS D C,et al.Electricity demand loads modeling using Auto-Regressive Moving Average (ARMA) models [J].Energy,2008,33(9):1353-1360.

Modal Parameter Identification of Large Cable-Stayed BridgeBased on IEEMD and ARMA Algorithm

YUAN Quan1, HE Jie2

(1. Guizhou Highway Bureau, Guiyang 550003, Guizhou, P.R.China; 2. School of Architecture & Civil Engineering, Southwest Jiaotong University, Chengdu 610031, Sichuan, P.R.China)

An improved ARMA identification method based on IEEMD decomposition algorithm was proposed. Firstly, an IEEMD analysis for the measured acceleration signal was carried out, and then the question whether there was a modal aliasing in the obtained intrinsic mode functions (IMFs) was verified by using clustering analysis. Secondly, the fuzzy comprehensive evaluation method was used to calculate the fuzzy similarity coefficients between eachIMFand the measured signal so as to select the effectiveIMFcomponent, and then the principal component analysis and Pareto Diagram method were used to reconstruct the signal of preservedIMFs, so that the effective decomposition of the measured signal and the noise attenuation effect could be achieved. Finally, the reconstructed dynamic signal was regarded as the input of ARMA algorithm to identify the modal parameters. Through analyzing the error percentage between each order’s frequency and truth value by comparative analysis, it is indicated that the vibration signal processed by IEEMD method is used as the input of the ARMA algorithm, so it can get the frequency which is most close to the real values and the error percentage is below 3%. The results verify that the proposed identification method can effectively identify the frequency of the cable-stayed bridge.

bridge engineering; IEEMD; fuzzy comprehensive evaluation method; principal component analysis; Pareto diagram method; ARMA

2015-04-28；

2015-07-22

袁 泉(1970—)，男，贵州习水人，高级工程师，主要从事路桥建设与管理工作。E-mail：yq2439@163.com。

何 杰(1990—)，男，四川资阳人，硕士研究生，主要从事桥梁结构健康监测与损伤识别方面的研究。E-mail：1103765724@qq.com。

10.3969/j.issn.1674-0696.2016.01.03

U446.3

A

1674-0696(2016)01-010-06