终端区关键定位点调整对交通流影响研究*

廖志华　张洪海　许　炎

(南京航空航天大学民航学院　南京　211106)



终端区关键定位点调整对交通流影响研究*

廖志华张洪海许炎

(南京航空航天大学民航学院南京211106)

摘要：为优化终端区空域结构，提高空域运行效率，基于广义跟驰理论和终端区基本运行规则建立了进离场航空器运动模型与空域结构网络模型，仿真分析了等待定位点调整对交通流流量、速度及密度等参数的影响.仿真分析结果表明，交通流对等待定位点位置调整十分敏感，且等待定位点与下游汇聚点的航段长度与进场空中延误具有显著的二次非线性关系，该航段长度越长，交通流速度减小和密度增大越快，进入拥塞状态越迅速，同时拥塞消散越缓慢.

关键词：航空运输；交通流；空域结构；跟驰模型；终端区

0引言

终端区是空域拥堵、航班延误易发的空中交通管制区域.终端区空中交通流是进离场航班在有限的时间和空间内的聚散现象，能反映终端区特定时空内航班流量分布状况、密集程度和运行效率等.研究终端区空域结构调整对交通流的影响规律对优化终端区空域网络、提高运行效率、降低航班延误等具有重要理论价值.终端区交叉汇聚点、速度或高度限制定位点、等待定位点及重要导航台等关键定位点的设置直接影响空域网络静态构型，引起交通流与空域网络复杂的互适应变化，但有关空域对交通流的影响机理研究尚待深入.

目前国内外研究主要集中在终端区空域结构优化、进离场流量管理等应用方法策略方面，包括基于空域灵活使用的终端区扇区优化划设方法[1-3]、航路与流量协同管理策略[4]等，这些研究均侧重于宏观方面的扇区优化或流量调配，缺乏空域对交通流影响内在机理的微观剖析.近年来，国内外学者开始关注空中交通流蕴含的科学规律问题，Menon等[5]建立了简化空中交通流欧拉数学模型，Bayen等[6]把欧拉网络模型转化成线性网络控制问题，Sun等[7]对比分析了不同空中交通流模型的特点，张洪海等[8-9]初步探讨了空中交通流相位问题，并分析了空中交通流基本参数关系，但上述研究主要集中在交通流内在特性上，空域结构(如关键定位点位置、航线长度、交叉汇聚方式)对交通流的影响机理鲜有研究.为深入探析空域结构对交通流的影响，文中从微观航空器飞行行为出发，基于终端区空域网络、微观跟驰原理和交通管制策略，建立了终端区进离场交通流微观模型，仿真分析了等待定位点位置调整对交通流参数及其关系的影响，着重分析速度-密度关系随定位点位置调整的变化规律，以期为优化进离场航线网络、提高空中交通运行效率提供理论依据.

1进离场微观建模

航空器进场飞行是一个逐渐减速和下降高度的过程，离场飞行则是一个不断加速和爬升高度的过程.根据终端区交通运行基本规则，进场航空器主要通过调速实现与前机保持安全间隔；当后机速度过大时，则可采取适当偏航机动飞行的策略；当跑道资源不足时，管制员通常对进场航空器发等待指令(如进入等待空域或雷达引导)，确保交通流畅通运行.

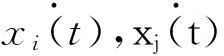
1.1调速跟驰建模

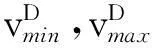
(1)在进场阶段或完成爬升后的离场阶段，航空器可通过速度调整达到保持安全间隔的目的.

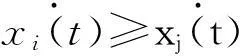
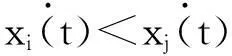
若前机匀速飞行，当二者间隔达到D+ΔS，后机将以前机速度为目标速度进行减速跟驰，则

(2)设经过时间T后，前后机速度相等，不妨设此时间隔为D1≥D，则

由上式可得

(4)当式(4)成立时，后机以前机速度为目标速度进行减速跟驰，能保证基本安全间隔，反之后机需要采取机动跟驰.

若前机以v0(t)为目标速度匀减速飞行，当二者间隔达到D+ΔS，后机将以v0(t)为目标速度进行减速跟驰，同理有

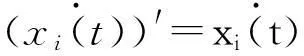
(6)若前机以v0(t)为目标速度匀减速机动飞行，同理得

(7)

1.2机动跟驰建模

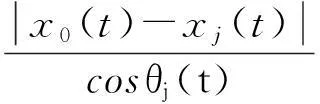
(8)

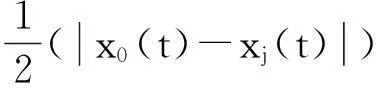
同理，若前机匀减速飞行，后机最小出航角为

(9)

式中：θj(t)≤θmax，θmax为考虑航空器性能和飞行安全所规定的最大机动角度.

1.3盘旋等待建模

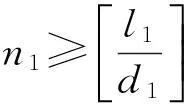
设盘旋等待速度为v0，标准等待时间为T0.当管制员允许后机“超车”时，等待空域的航空器i在时刻t+T0需重新选择插队时机，其出等待约束为

(10)

1.4进离场协调策略

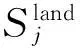
(11)

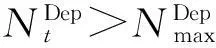
(12)

2空域结构建模

终端区空域结构较一般航路结构复杂，是一个多交叉、多发散、多汇聚结构的有向网络.根据终端区基本运行规则，该空域网络决定了不同方向交通流的聚散方式，不同节点位置和节点容量决定了航空器飞行时间和调配策略，因此终端区空域结构建模需充分考虑节点性质、节点入度与出度、节点速度限制、航段长度与方向等信息.

一般地，终端区进场航线构成的网络可抽象为有向图，由节点和有向边构成，用B=(P,E)表示.有向边(Pi,Pj)∈E存在一个理论容量Cij(Cij≥0)，则该网络的静态拓扑结构可描述为B=(P,E,C).

用n阶广义邻接矩阵A(t)=[aij(t)]n×n表示具有n节点网络的连通性和有向性，即

(13)

当aij(t)+aji(t)=2，则aij(t)=aji(t)=1,i=j，表示节点pi为等待空域的出入口，允许交通流在此节点循环运行；当aij(t)+aji(t)=0且aij(t)≠0，表示存在节点pi到节点pj单向航段或节点pj到节点pi单向航段；当aij(t)=0时，表示节点pi与pj无航段.

用n阶权值矩阵L(t)=[lij(t)]n×n为各航段有效长度，即

(14)

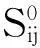
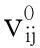
则B=(P,E,C)可描述为

(15)

引入进场空中平均延误delayA：即所有进场航空器从进入终端飞行至降落跑道的实际空中飞行时间与预计空中飞行时间差值的平均值.在终端区大流量运行时，汇聚航段的冲突频率高，调速、机动跟驰行为骤增，等待程序是完成进场流量控制与疏散的关键策略，研究等待定位点位置调整对交通流的影响显得尤为重要.

3仿真实验与分析

3.1仿真设置

由于真实雷达数据是人工干扰后的结果，终端区运行的流量被严格控制在一定范围，不能全面、客观反映交通流的特性.分析某大型机场航班到达时间间隔可知，其航班流时间间隔满足负二项式分布，故文中航班计划为满足负二项式分布的随机航班流，通过改变等待定位点地理坐标(xhold,yhold,zhold)实现空域结构调整，仿真得到不同位置下的交通流运行数据，基本仿真参数见表1.

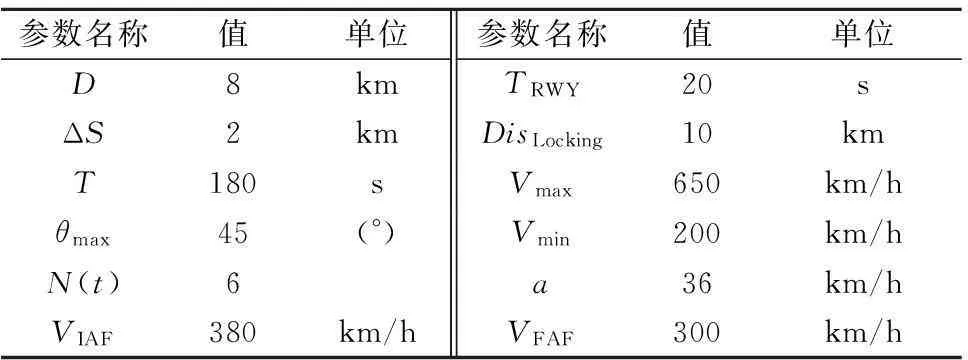
表1　基本仿真参数

文中基于NetLogo仿真平台编写JAVA程序实现了模型仿真与数据输出，仿真空域结构与仿真界面见图1.IAF点为等待定位点，位于图1a)灰色三角形覆盖区域内.

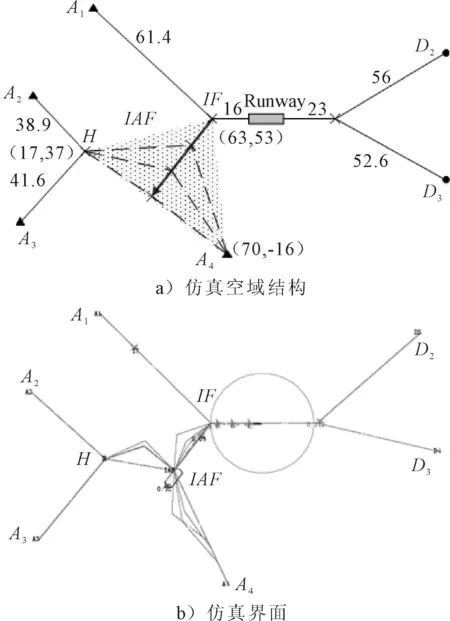
图1　仿真空域结构与界面

3.2实验与分析

在进场优先策略下，离场过程简单，文中选取进场交通流为研究对象，以等待定位点地理坐标为空域结构调整的参数，仿真分析了不同坐标下进场交通流延误、流量、速度以及密度等关键性指标.

1)IAF坐标与delayA分析改变IAF点坐标时，空中延误delayA呈现一定的规律性变化(见图2，颜色越深表示进场空中延误越小).仿真结果表明，当IAF点越靠近下游汇聚点IF时，delayA越小；反之，delayA越大.

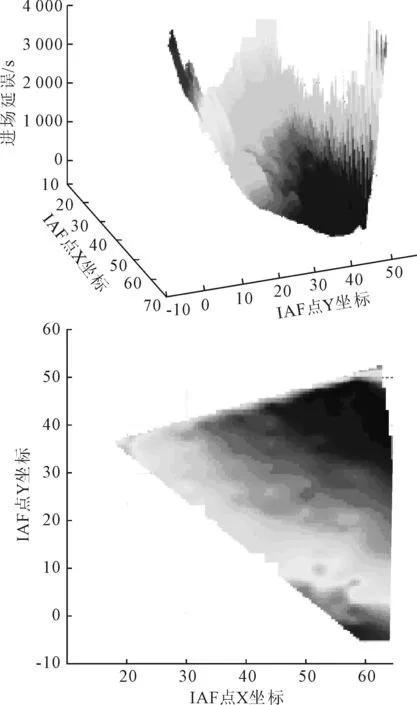
图2　IAF坐标与delayA关系

为验证delayA与航段IAF～IF长度SIAF～IF的相关关系，将仿真得到的delayA与SIAF～IF进行相关性分析.图3为SIAF～IF与delayA散点图，随着SIAF～IF不断增大，delayA呈二次非线性增长.数据拟合结果表明，SIAF～IF与delayA存在显著的二次非线性关系，拟合曲线为y=2.124 6x2-29.357x+253.06，相关系数R2=0.954 3>0.95.

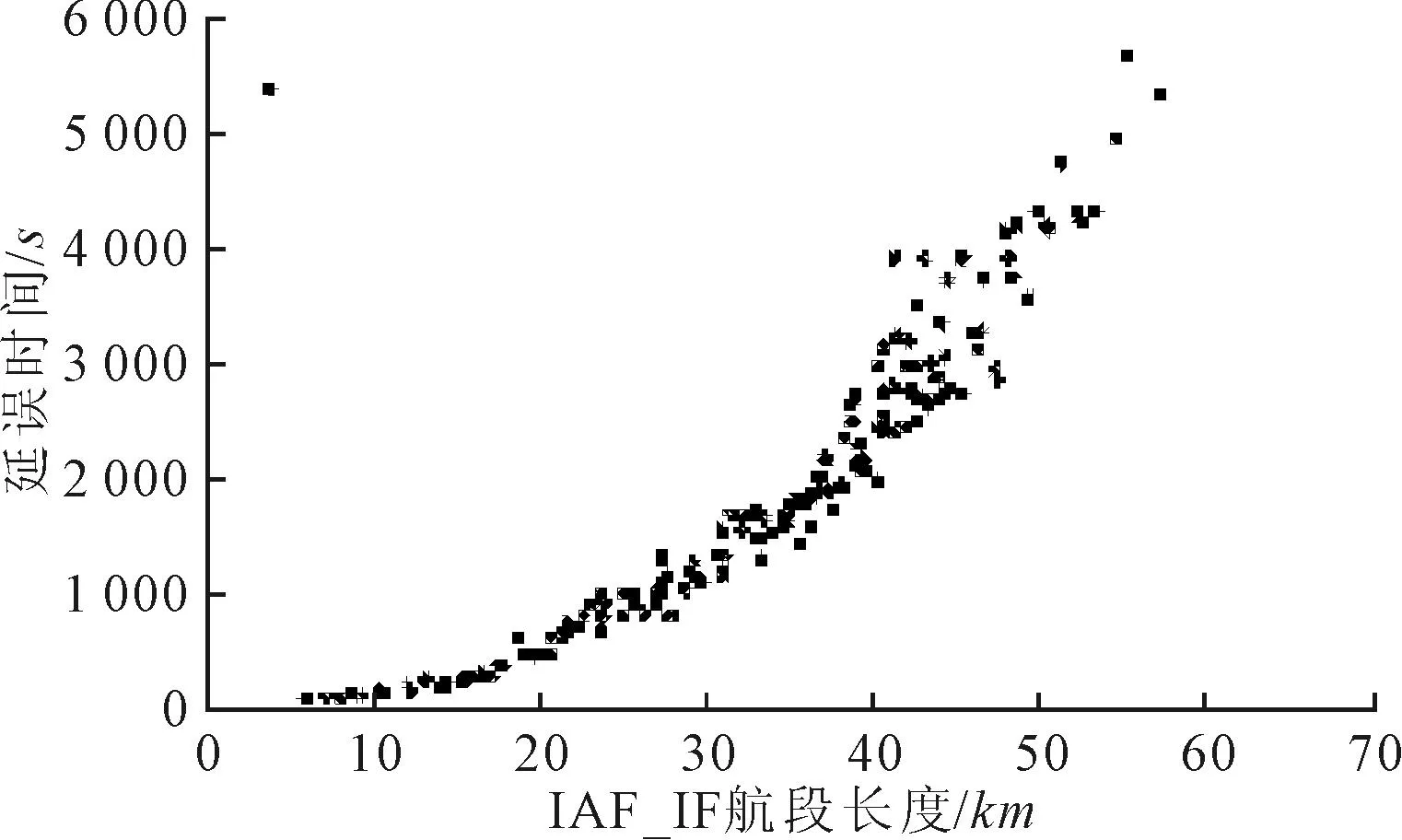
图3　SIAF～IF与delayA关系

选取航段IAF～IF长度SIAF～IF作为空域关键定位点调整的依据，进一步研究SIAF～IF大小对交通流运行的影响.

2)SIAF～IF对速度、密度的影响delayA的大小反映了交通流运行畅通程度，delayA越大，交通流内部飞行冲突越多，航空器执行调速跟驰、机动跟驰及等待程序频率越高，造成额外飞行时间增加越多.由于delayA与SIAF～IF存在二次非线性关系，不妨选取SIAF～IF=10 km、SIAF～IF=20 km、SIAF～IF=30 km、SIAF～IF=40 km 4个典型的点进一步分析空域调整对交通流的影响.

不同SIAF～IF航段长度下的进场平均速度、平均密度随时间变化曲线见图4.由图4可知，SIAF～IF航段长度越小，其进入拥塞状态越缓慢且拥塞消散越快；当SIAF～IF=10 km时，交通流并未进入拥塞状态，当SIAF～IF=40 km时，交通流在第4个时间片即进入拥塞状态.分析空域结构和仿真细节可知，当SIAF～IF较小时，SH～IAF、SA4～IAF较大，航段H～IAF和A4～IAF上的交通流主要通过调速跟驰完成汇聚，机动跟驰较少；同时，航段A1～IF比IAF～IF航段长度大得多，通过等待定位点的交通流几乎不受A1～IF上交通流的影响，因此交通流速度下降缓慢，密度增加平缓，在进入拥塞状态之前即完成进场.

密度与速度曲线变化过程内在机理相似，即航段汇聚长度和相互影响航段范围的变化导致了交通流内部行为的适应性改变，从而引起交通流速度、密度的规律性变化.

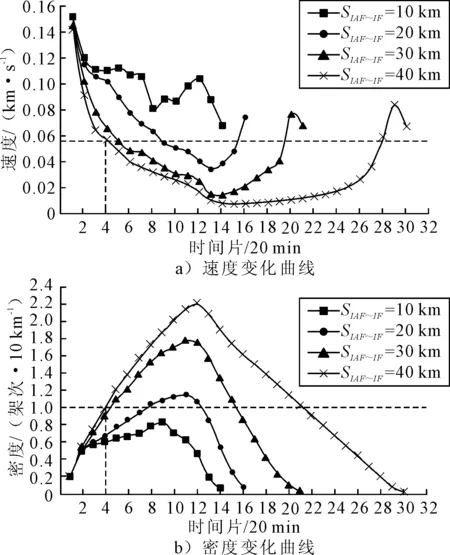
图4　速度、密度变化曲线

3) 速度-密度关系曲线在大流量仿真运行条件下，进场交通流的速度、密度变化曲线均能完整体现.图5为4种空域结构下的速度-密度关系散点图.

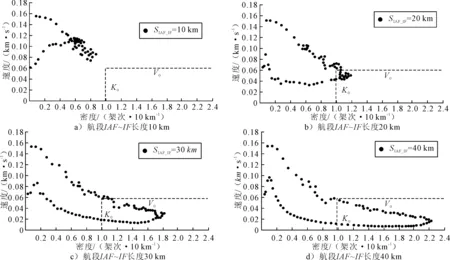
图5　不同空域结构下的速度-密度关系

进场交通流的速度与密度之间存在密切的相互变化关系，且对关键等待定位点位置具有较强的灵敏性.当SIAF～IF=10 km时，随着密度的增大，交通流速度先缓慢减小，随着加入进场的流量减少，交通流密度减小，速度反向增大；交通流的速度和密度均未达到临界值，处于高流量运行状态.当SIAF～IF≥20 km时，速度随着密度的增大而减小并进入拥塞状态；当拥塞程度进一步加剧时，速度继续减小；随着加入进场的流量减少，密度逐渐减小，在拥塞消散过程中速度则首先反向减小，随后缓慢增大；SIAF～IF长度越大，交通流进入拥塞状态越快，拥塞消散越慢.结合空域构型分析，SIAF～IF增大造成航段IAF～IF交通流受航段A1～IF影响范围变大，且上游交通流加入等待程序更快、等待空域流量增大明显，最终导致交通流更快地进入拥塞状态并促使拥塞加剧，拥塞消散越来越缓慢.

4结论

1) 等待定位点与下游汇聚点的航段长度与进场空中延误具有显著的二次非线性关系；

2) 该航段长度越大，交通流速度减小和密度增大越快，进入拥塞状态越迅速，同时拥塞的消散越缓慢，能够为终端区空域结构的划设、调整提供依据，对优化终端区运行规则、提高运行效率、降低航班延误等具有重要的指导意义和应用价值，同时也丰富了空域结构调整对交通流影响机理的理论.

参 考 文 献

[2]SAVAI M P, LI J, WANG T, et al. An algorithm for adaptable dynamic airspace configuration[C].The Proceedings of the AIAA Aviation Technology, Information, and Operations Conference, Fort Worth, TX. 2010.

[3]张明,韩松臣.基于空域灵活使用的终端空域规划设计方法[J].交通信息与安全,2013,31(5):5-8.

[4]孙晓阳,胡明华,张洪海.空域和流量协同管理建模与仿真[J].交通运输工程学报,2010,10(1):72-76.

[5]MENON P K, SWERIDUK G D, BILIMORIA K D. A new approach for modeling, analysis and control of air traffic flow [J]. AIAA Journal of Guidance, Control and Dynamics, 2004,27(5):737-744.

[6]BAYEN A, RAFFARD R, TOMLIN C. Adjoint-based control of a new Eulerian network model of air traffic flow [J]. Transactions on Control Systems Technology, 2006,14(5):804-818.

[7]SUN D, STRUB I, BAYEN A. Comparison of the performance of four eulerian network flow models for strategic air traffic management [J]. Networks and Heterogeneous Media, 2007,2(4):569-594.

[8]张洪海,杨磊,别翌荟,等.终端区进场交通流广义跟驰行为与复杂相变分析[J].航空学报,2015,36(3):949-961.

[9]ZHANG H H, XU Y, YANG L, LIU H. Macroscopic model and simulation analysis of air traffic flow in airport terminal area [J]. Discrete Dynamics in Nature and Society，2014(15)：2014.

Research on the Influence of Airspace Key Fix Point Adjusting on Air Traffic Flow in Terminal Area

LIAO ZhihuaZHANG HonghaiXU Yan

(CollegeofCivilAviation,NanjingUniversityofAeronautics&Astronautics,Nanjing210016,China)

Abstract：In order to optimize airspace structure and improve its operational efficiency, a motion model for aircrafts departure and arrival and an airspace structure network model are presented based on the generalized following theory and basic operation rules in terminal area. The airspace structure is changed by adjusting the coordinate of Holding Fix point and the influence of airspace structure adjusting on air traffic flow is analyzed by simulation. The simulation results show that the traffic flow is quite sensitive to coordinate adjusting of Holding Fix point. There is an obvious quadratic non-linear relationship between the airplane delay and length of Holding Fix point and downstream convergent point. With this length increased, it is found that the air traffic flows more slowly and the air traffic density increases more rapidly. In addition, the increase of the length would turn the air traffic into congested status more rapidly and make the congestion dissipate more tardily.

Key words：air transportation; traffic flow; airspace structure; following model; terminal area

doi:10.3963/j.issn.2095-3844.2016.02.028

中图法分类号：V355

收稿日期：2016-02-07

廖志华(1989- )：男，硕士生，主要研究领域为大型机场及复杂空域运行评估

*国家自然科学基金项目资助(61104159)