四桨双舵船操纵运动特性数值预报方法研究*

王慧婷　毕　毅　姚朝帮

(91404部队91分队1)　秦皇岛　066000)　(海军工程大学舰船工程系2)　武汉　430033)



四桨双舵船操纵运动特性数值预报方法研究*

王慧婷1)毕毅2)姚朝帮2)

(91404部队91分队1)秦皇岛066000)(海军工程大学舰船工程系2)武汉430033)

摘要：基于MMG模型，结合多桨船船后桨舵干扰的复杂特性，建立了四桨双舵船操纵性预报模型.以某四桨双舵船为研究对象，采用粘性CFD方法计算船体水动力导数、船-桨-舵干扰系数，龙格-库塔算法求解运动微分方程，开展了回转运动及Z形运动的数值预报，并与试验结果进行了对比分析，研究结果表明：回转运动中运动轨迹、角速度、横倾角及Z形运动中初转期、超越角的仿真结果与试验结果吻合良好，证明了此数值预报方法的可行性.

关键词：MMG模型；四桨双舵船；操纵性；数值仿真

0引言

船舶操纵性是船舶重要性能之一，对操纵性能进行准确预报是船舶设计的重要任务.预报操纵性有半理论半经验估算、自航模试验和计算机数值模拟方法3种，所依据的操纵运动方程有代表性的有2种：1967年Abkowitz推导出的运动方程和1977年日本操纵性数学模型小组提出的MMG方程.MMG方程以船、桨、舵单独性能为基础，合理表示出了作用于船体上的流体动力，得到了广泛的应用.起初，MMG方程的研究对象为单桨单舵船，H.Yasukawa等[1]以KVLCC2为研究对象，对1∶110,1∶45.7的船模及1∶1的实船基于MMG模型进行操纵性预报，对比尺度效应对预报结果的影响.随着深入研究，学者们将MMG模型的适用范围扩大到双桨双舵船上.Kobayashi等[2]基于MMG模型对双桨双舵船巡航速度和低速情况下提出一种数学模型，并用自航模试验进行了验证.随之Yumuro[3]基于MMG模型开始研究双桨单舵船的数学模型及对于舵的有效来流速度.Hamamoto等[4]将MMG模型应用于单桨双舵船的操纵性预报中.针对4桨2舵船，一些学者尝试将MMG方程应用于其静水中的操纵运动仿真[5-10]，但公开发表的文献中对水动力导数及船-桨-舵干扰系数均采用估算公式估算，估算结果存在着一定的误差.

本文基于MMG方程，在数值模拟斜航、纯首摇、漂角和首摇组合3种PMM运动求得的水动力导数及数值模拟船模直航操舵运动、运用估算公式等方法得到的船-桨-舵干扰系数基础上，采用四阶龙格-库塔算法对MMG操纵运动数值模型中的运动微分方程进行求解，开发出了四桨双舵船的操纵运动仿真程序，对回转、Z形运动进行数值仿真，并将结果与自航模试验结果进行对比，验证仿真结果的可靠性.

1研究对象

本文研究对象为4桨双舵船模，该船模量纲一的量化主要参数见表1.船后对称布置4桨2舵，舵位于内桨的正后方.桨舵相对位置见图1.其中：L为船模总长.

2坐标系定义

船舶运动中采用两种坐标系，即固定坐标系和运动坐标系，见图2.2种坐标系都为右手坐标系.固定坐标系固结于地球，记为O0X0Y0，运动坐标系固结于船体，其坐标原点O在船体重心G点处，X轴沿首尾方向，船首方向为正，记为OX，OY轴右舷为正，OZ轴垂直向下为正.左舵为负，右舵为正.

表1　船模量纲一的量化主要参数

图1　桨舵相对位置

图2　运动参量及坐标系

34桨双舵船操纵运动数学模型

因4桨2舵船在操纵运动过程中会产生较大的横倾角，数值仿真时选用4自由度运动模型，即

(1)

式中：下标H，P，R分别为船体、螺旋桨和舵；X，Y，N，K分别为操纵运动中船模所受的纵向力、横向力、摇首力矩及横倾力矩；IX，IZ分别为船对动坐标系GX，GZ轴的转动惯量；φ为横倾角；m11，m22为船舶运动时沿X，Y轴方向的附加质量，m66为绕Z轴的附加惯性矩，采用周昭明回归公式[11]进行估算；m44为绕X轴的附加惯性矩，用杜埃尔公式[12]进行估算，具体计算式为

(2)

(3)

(5)

式中：Zg为重心垂向坐标.

3.1船体水动力计算

船体所受的纵向力、横向力、摇首力矩及横倾力矩为

(6)

式中：纵向力的水动力导数采用经验公式进行估算，而横向力和力矩的水动力导数采用CFD方法数值模拟得到.

(7)

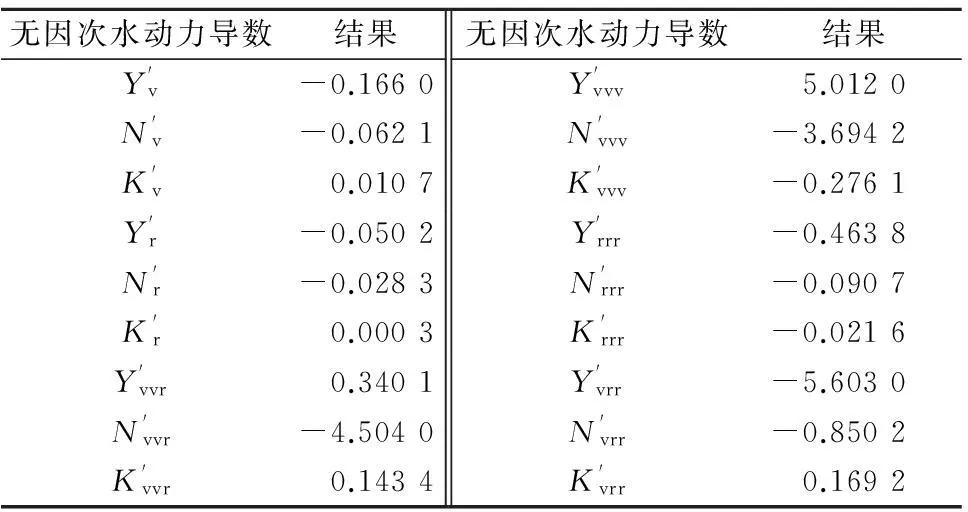
表2　无因次水动力导数结果

(8)

(9)

3.2螺旋桨水动力计算

对于4桨船舶，运动中双内桨与双外桨所受的实效伴流分数wp不同，则所产生的推力也不同.表达式如下.

式中：下标n，w和(n)或(w)分别表示内桨、外桨和内桨或外桨；k0，k1，k2由螺旋桨敞水曲线拟合得到.

对于螺旋桨推力减额分数tp的求解，根据数值模拟船模直航运动得到四个螺旋桨产生的总推力T，及模拟不带螺旋桨进行直航运动时船体的阻力R，可得直航时螺旋桨的推力减额tp，由于四桨船的推力减额分数尚无成熟的理论与试验分析方法，计算时认为4个螺旋桨的推力减额分数相同，以简化计算过程.当船体进行操纵运动时，tp基本保持不变.

对于实效伴流wp的求解，根据船模直航运动中测得两内桨与两外桨的推力Tn，Tw及螺旋桨的敞水性能曲线，利用等推力法求得2内桨与2外桨的进速Van，Vaw，进而计算出直航时2内桨与2外桨的实效伴流分数wp0=1-Va/V.操纵运动中的实效伴流wp与直航时的伴流分数wp0存在着一定的关系，关系式如下.

(11)

求得螺旋桨的常数干扰系数见表3.

表3　桨的常数干扰系数

3.3舵水动力计算

在操纵运动中，内、外舵产生的舵力不同，表达式如下.

(12)

式中：(n)或(w)表示内舵或外舵；fa=6.13λ/(2.25+λ)，其中舵展舷比λ=h/b；uPn，kTn，Jn均为内桨的运动参量，因双舵位于双内桨正后方，且距离很近，只考虑双内桨对舵的影响.

双舵产生的力和力矩的表达式如下.

式中：系数tR，αH，xH由数值模拟船模直航操舵运动，测得不同舵角下船模所受的水动力及左右舵的舵力，对水动力随舵分力变化曲线进行线性拟合得到.

求得的舵的常数干扰系数见表4.

表4　舵的常数干扰系数

4数值仿真结果分析

4.1回转运动仿真结果

通过对MMG操纵性模型的求解，得到船模回转运动过程中的结果，并对运动轨迹、角速度、横倾角随时间的变化情况进行输出绘制.将仿真结果与自航模操纵性试验结果进行对比分析.图3～4及表5～6分别给出了弗劳德数Fr=0.162 8、舵角δ=±15°时回转运动中各参量的仿真结果与试验结果的对比图及对比结果.

图3　δ=-15°时回转运动参量变化情况

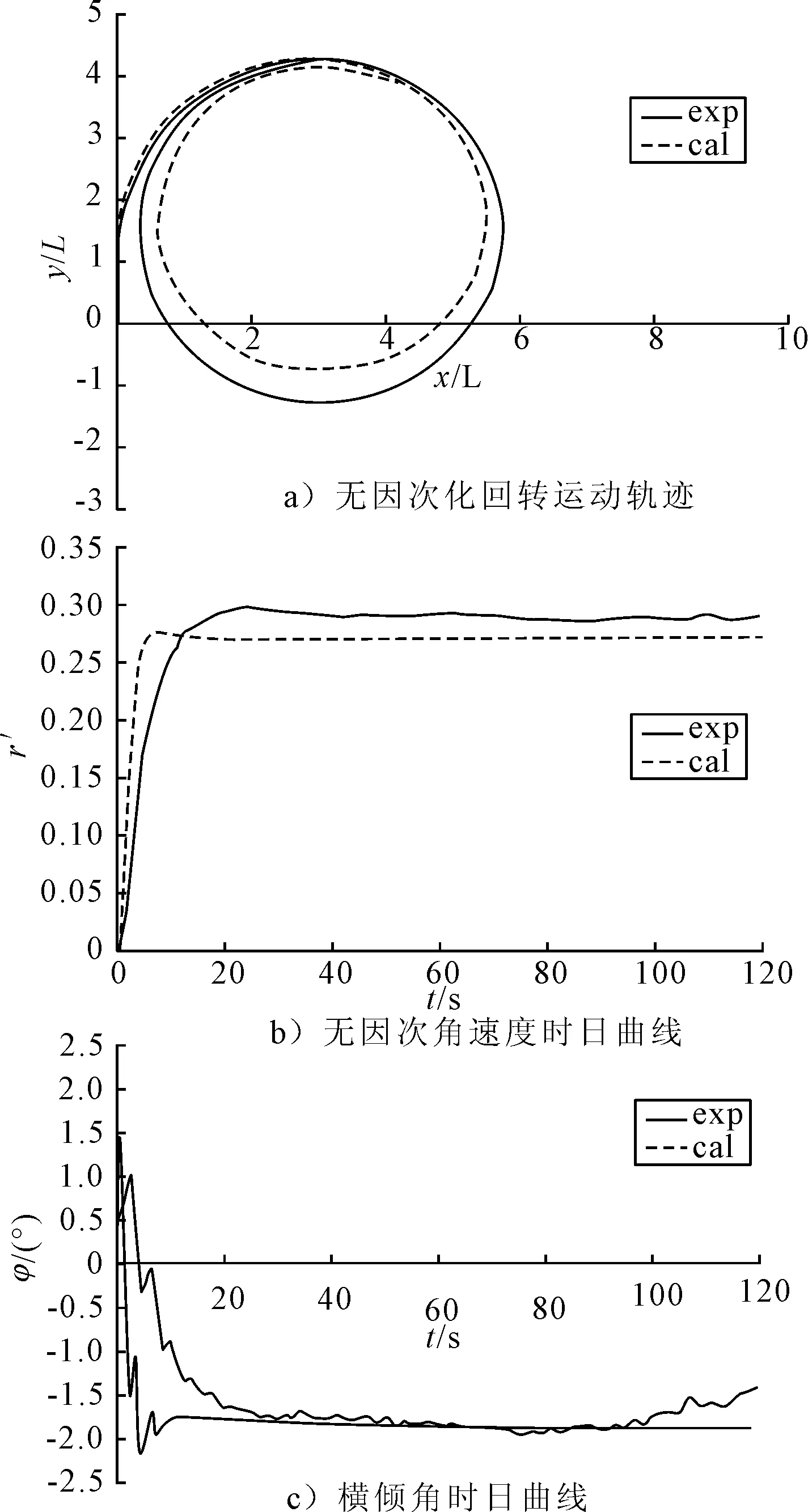
图4　δ=15°时回转运动参量变化情况

无因次回转直径D'无因次角速度r'横倾角φ/(°)试验结果5.137-0.2932.402仿真结果5.234-0.2671.994误差/%1.898.8716.99

表6　δ=15°回转运动时试验与仿真结果对比

由图3～4及表5～6可知，仿真结果与试验结果吻合良好，误差均在20%以内.自航模试验因受外界环境影响，所得结果会在范围内有一定的波动，而数值仿真则避免了这个影响，运动稳定后，各参量均稳定于某一值.同一舵角下，打左右舵时，各参量均体现出了很好的对称性.

4.2Z形运动仿真结果

对船模进行弗劳德数Fr=0.162 8、执行舵角ψe/δe=±10°/±10°和ψe/δe=±20°/±20°的Z形操舵运动，得到运动过程中舵角和首向角的变化情况.图5～6及表7～8分别给出了+20°/+20°，-20°/-20° Z形运动时舵角、首向角数值仿真结果和试验结果的时历曲线及对比结果.

图5　+20°/+20° Z形运动时的舵角和首向角时历曲线

初转期t'a/s第一超越角ψov1/(°)第二超越角ψov2/(°)试验结果1.80611.76014.605仿真结果1.4158.45911.305误差/%21.6528.0722.60

图6　-20°/-20° Z形运动时的舵角和首向角时历曲线

初转期t'a/s第一超越角ψov1/(°)第二超越角ψov2/(°)试验结果1.80613.08414.547仿真结果1.4178.65011.407误差/%21.5433.8921.59

由图5～6及表7～8可知，数值仿真所得的初转期和超越角均小于试验结果，存在着一定的误差.因对部分干扰系数进行了近似处理：对于推力减额分数，认为四个螺旋桨是相同的；忽略了双外桨对舵伴流的影响，只考虑了双内桨的影响；利用双桨双舵船部分干扰系数的估算公式对此四桨双舵船相应系数进行估算；直接根据其他类似四桨双舵船的干扰系数对此船部分干扰系数进行了选取，数值仿真结果与试验结果存在着误差；因Z形试验多次打舵，前一次打舵数值仿真与试验的误差将会影响下一次的打舵响应，因此，随着打舵次数的增加，偏离将越来越大.

5结论

本文基于MMG模型，利用求得的水动力导数及船-桨-舵干扰系数，分别求得船体、螺旋桨、舵上所受的水动力及运动中产生的附加质量，采用四阶龙格-库塔算法对MMG操纵运动数学模型中的运动微分方程进行求解，开发了四桨双舵船操纵运动仿真程序，并对回转、Z形运动进行数值仿真，所得结论如下.

1) 回转运动中回转运动轨迹、角速度、横倾角的仿真结果与试验结果均吻合良好，误差在20%以内.

2) Z形运动中初转期、超越角的仿真结果变化趋势上与试验结果一致，数值上稍有偏差.

参 考 文 献

[1]YASUKAWA H, YOSHIMURA Y. Introduction of MMG standard method for ship maneuvering predictions[J]. Journal of Marine Science and Technology,2015,20:37-52.

[2]KOBAYASHI H, ISHIBASHI A, SHIMOKAWA K, et al. A study on mathematical model for the maneuvering motions of twin-propeller twin-rudder ship[J].Journal of Japan Institute of Navigation,2014，91:263-270.

[3]YUMURO A. Some experiments on rudder force of a twin-screw ship with a single rudder[J]. Journal of the Kansai Society of Naval Architects Japan,2014，194:53-64.

[4]HAMAMOTO M, ENOMOTO T. Maneuvering performance of a ship with Twin rudder system[J]. Journal of Society Naval Architects Japan,2013，181:197-204.

[5]莫建.波浪中船舶六自由度操纵运动数值仿真[D].哈尔滨：哈尔滨工程大学，2009.

[6]祁宏伟.波浪中船舶六自由度操纵/摇荡耦合运动仿真研究[D].哈尔滨：哈尔滨工程大学，2008.

[7]刘杨.船舶操纵运动仿真中的水动力系数敏感性分析[D].哈尔滨：哈尔滨工程大学，2008.

[8]吴晗.大型舰船操纵性理论预报及视景仿真[D].哈尔滨：哈尔滨工程大学，2010.

[9]刘伟明.波浪中船舶六自由度“操纵-摇荡”耦合运动数值仿真[D].哈尔滨：哈尔滨工程大学，2010.

[10]徐明彩.大型水面舰船操纵性仿真软件开发[D].哈尔滨：哈尔滨工程大学，2011.

[11]范尚雍.船舶操纵性[M].北京:国防工业出版社,1988.

[12]盛振邦,刘应中.船舶原理[M].上海:上海交通大学出版社,2003.

[13]松本.操縱運動の數學モテルにおけら船體·推進器·舵的干涉效果[R]. 關西:關西造船協會志，1983.

[14]范尚雍,程智斌,吕韶康.高速双桨双舵船的船-桨-舵之间的水动力干扰[J].中国造船，1989(2):25-32.

Numerical Prediction Method of Four-propeller Twin-rudder Ship Maneuvering Characteristics

WANG HuitingBI YiYAO Chaobang

(DepartmentofNavalArchitecture,NavalUniversityofEngineering,Wuhan430033,China)

Abstract：Based on the MMG model and combined with the complex characteristics of the multi-propellers ship's interaction between propeller and rudder, four-propeller twin-rudder ship maneuverability prediction model is established. The study focuses on a four-propeller twin-rudder ship, using CFD method to calculate the hydrodynamic coefficients as well as hull-propeller-rudder interference coefficients and using Runge-kutta algorithm to solve the differential equation of motion. Numerical prediction of turning motion and zigzag motion is carried out. Meanwhile, the prediction results are compared with the test results. The comparison shows that the simulation results agree well with experimental results for motion trajectory, angular velocity and heeling angle in turning motion and first rollover and overshoot angle in zigzag motion. The results prove the feasibility of this numerical prediction method.

Key words：MMG model; four-propeller twin-rudder ship; maneuverability; numerical simulation

doi:10.3963/j.issn.2095-3844.2016.02.034

中图法分类号：U631.1

收稿日期：2016-02-14

王慧婷(1990- )：女，助理工程师，主要研究领域为舰船流体动力性能

*水动力学重点基金项目(9140A14030712JB11044)、海军工程大学自然科学基金项目(435517J4040)资助