多馈入直流输电系统谐波相互影响的研究

刘婷婷， 文 俊， 乔光尧， 符茜茜， 周胜军

(1. 华北电力大学电气与电子工程学院， 北京 102206； 2. 国网智能电网研究院， 北京 102211)

多馈入直流输电系统谐波相互影响的研究

刘婷婷1， 文 俊1， 乔光尧2， 符茜茜1， 周胜军2

(1. 华北电力大学电气与电子工程学院， 北京 102206； 2. 国网智能电网研究院， 北京 102211)

首先给出了交流系统各主要元件谐波频率下的数学模型，利用Ward多端等值法推导出多馈入直流输电系统各直流接入点在谐波频率下的节点导纳矩阵，进而可以得到各直流接入点的谐波电压。对上海电网500kV电压等级电网进行了等值并通过计算得到不同运行方式下各直流接入点的电压总谐波畸变率的范围，经分析可知上海地区多馈入直流输电系统谐波相互影响很小，各直流接入点电压的畸变主要受自身直流线路谐波的影响。

多馈入直流输电； 谐波影响； 数学模型； Ward多端等值法； 电压总谐波畸变率

1 引言

高压直流输电系统在电能传输的过程中会在交直流侧产生各种谐波，在对电力系统电能质量及通信系统产生影响的同时也给换流变压器造成了影响，使其噪音过大、局部过热，甚至损坏[1,2]。高压直流输电系统还有可能在交直流侧引起谐波放大现象，造成系统不稳定[3]。由于我国能源与负荷分布的特殊性，高压直流输电工程在我国得到了极大的发展[4]，使得上海等地区形成了多条直流同时馈入的格局，即多馈入直流(Multi-Infeed DC, MIDC)输电系统。而从直流接入点注入到交流侧的谐波通过交流电网的传递必然会对系统中其他直流接入点产生一定的影响[5,6]。

本文主要研究了MIDC输电系统谐波的相互影响。首先介绍了各元件谐波频率下的数学模型，通过Ward多端等值法推导出MIDC输电系统各直流接入点间谐波频率下的节点导纳矩阵，进而得到各直流接入点的谐波电压。在以上理论的基础上，对上海电网500kV电压等级电网进行了等值，通过计算得到上海地区MIDC输电系统在不同运行方式下各直流接入点电压总谐波畸变率的范围，分析得知上海地区MIDC输电系统中某一直流线路接入点的电压总谐波畸变率主要受自身直流线路谐波的影响，而受其他直流线路的影响很小。

2 各元件谐波频率下的数学模型

在对系统谐波影响进行分析时，系统元件的谐波模型对分析结果的准确性和可靠性具有关键性的作用[7,8]。而对于一个已知电网，想要对它进行完整的描述是不可能的，所以需要将电网进行合理的等值[9]。以下给出主要网络元件的谐波模型。

2.1 输电线路模型

文献[10]指出，在谐波分析中，架空线路的模型主要取决于线路单位长度参数的频率特性及线路长度。对于是否采用线路的分布参数模型取决于线路长度和谐波次数，其临界长度为(241.39/h)km，其中h为谐波次数。可见，谐波次数越高，线路的分布参数特性影响越显著。为了计算准确，本文在各次谐波下均采用输电线路的分布参数模型。

假设潮流数据给出的输电线路数据是集总π模型参数，线路在基频下总的串联阻抗为R+jX，对地导纳为jB，令线路长度为l，线路单位长度参数为[11,12]：

(1)

(2)

谐波分析时，第h次谐波频率下线路单位长度的参数为：

(3)

(4)

因此，第h次谐波频率下的传播常数为：

(5)

第h次谐波频率下的波速为：

(6)

则线路的等效π模型如图1所示，参数分别为：

Zh=Rh+jXh=Zssinh(γl)

(7)

(8)

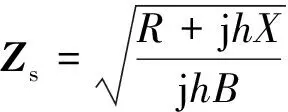
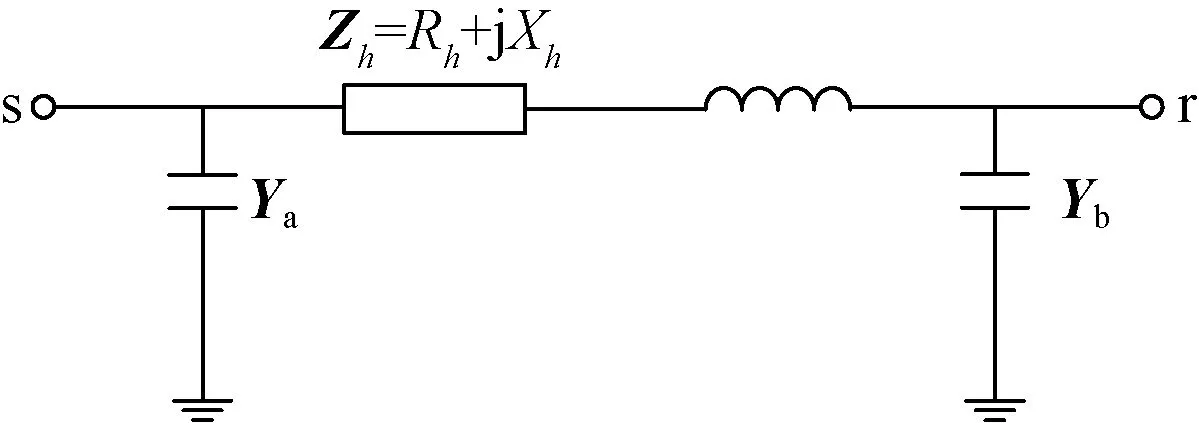
图1 输电线路的分布参数模型Fig.1 Distributed parameter model of transmission line

式(7)和式(8)表明，任意谐波频率下，考虑分布参数效应的等效π模型参数与线路长度l无关。因此，若已知输电线路的潮流计算数据，可以利用式(7)和式(8)直接导出用于谐波分析的等效π模型参数。

2.2 负荷模型

通常情况下，集中负荷所吸收的功率是十分容易获得的，在谐波分析中，可以用图2所示的并联模型来模拟负荷的阻抗。

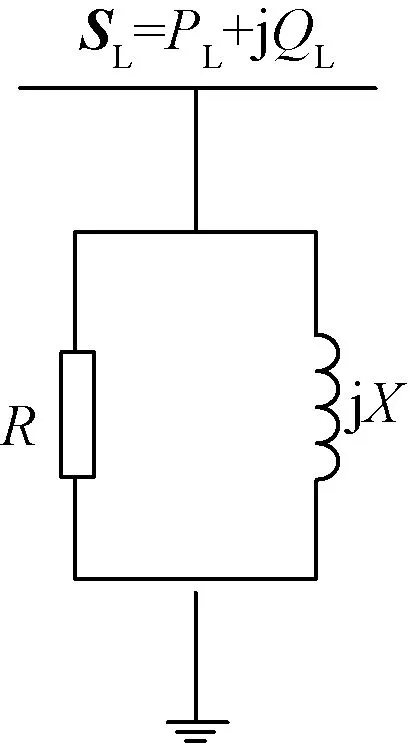
图2 负荷并联模型Fig.2 Parallel load model

假设在基波频率下负荷的等效模型为

ZL=RL+jXL

(9)

其中，RL为负荷的等效电阻；XL为负荷的等效电抗。二者可用式(10)得出：

(10)

在谐波分析中，当负荷为感性负荷时，第h次谐波下的等效阻抗可用式(11)表示，当负荷为容性时，第h次谐波下的等效阻抗可用式(12)表示：

ZL(h)=RL+jhXL

(11)

(12)

2.3 无功补偿模型

在实际分析中，当负荷点外接有较大容量的无功补偿装置时，由于电容的频率特性和电感全然不同，此时应将电容从综合负荷中分离出来作为一个独立支路对待[13]。其容抗可表示为:

(13)

如果已知电容器组的额定电压V(kV)和额定容量QC(Mvar)，则其容抗为：

(14)

电容在第h次谐波下的等效容抗为：

(15)

3 MIDC输电系统直流接入点谐波电压的计算

已知MIDC系统接入受端交流系统的节点在第h次谐波下的节点电压方程为：

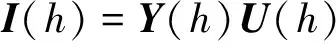
(16)

其中，I(h)为注入各节点的第h次谐波电流矢量；Y(h)为在第h次谐波下电网的节点导纳矩阵；U(h)为第h次谐波下各节点的电压矢量。

利用Ward多端等值法[14,15]，假设电网中共有n个节点，其中直流接入点为p个，并编号为1～p，则将式(16)展开得：

将式(16)表示成分块矩阵：

(17)

写成方程式为：

(18)

假设交流侧不存在背景谐波，所以I″h=0，由此可以得到：

(19)

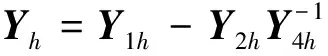
(20)

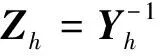
(21)

MIDC输电系统中的多回直流线路可以有多种不同的运行方式。不同谐波源作用下的同一节点的同一谐波频率分量存在相角差，在已知各直流线路注入交流侧谐波电流有效值的情况下，由于各分量之间的相角差不能确定，所以不能准确得到直流接入点在各谐波频率下的谐波电压，但是可以得到单回直流线路运行方式下各直流接入点的谐波电压有效值。多回直流线路运行方式下同一直流接入点同一谐波频率下的谐波电压有效值可以由所有参与运行的直流线路单独运行时此节点同一谐波频率下的谐波电压分量在不同相角下组合得到，通过Matlab程序可以求出所有组合下的最小谐波电压有效值Uh-min和最大谐波电压有效值Uh-max，再由式(22)和式(23)可以计算出多回直流线路同时运行方式下直流接入点的绝对最小电压总谐波畸变率THDu-min和绝对最大电压总谐波畸变率THDu-max，那么此运行方式下直流接入点的电压总谐波畸变率就界于绝对最小电压总谐波畸变率和绝对最大电压总谐波畸变率之间。

(22)

(23)

4 MIDC输电系统谐波相互影响的计算和分析

经过多年的发展，上海地区已经成为典型的含有多馈入直流输电系统的交流电网，其系统示意图如图3所示。其中包括±500kV的葛洲坝-南桥南、宜都-华新、荆门-枫泾以及±800kV复龙-奉贤四回直流线路。以下将在上海电网四回直流及500kV电压等级电网的基础上进行谐波计算和分析。

图3 上海电网500kV及部分220kV电压等级示意图Fig.3 Schematic of 500kV and part of 220kV voltage level network in Shanghai grid

4.1 电网等值

上海电网包含的多馈入直流输电系统中包括16个500kV站点以及4个直流线路受端站点，其中葛南直流工程通过220kV线路经变压器升压后接入到500kV电压等级电网中。本文主要研究接入上海电网的直流线路间谐波的相互影响，所以必须保留葛南站点，但需将其相关参数换算至500kV再进行电网等值。电网中220kV及以下电压等级电网与500kV电压等级电网具有电气联系，为了保证电网等效的完整性及计算结果的精确性，将其等效成负荷接入500kV电压等级电网。

按照第2节中各元件谐波频率下的数学模型，将500kV电压等级电网中各主要元件进行等效，并得到节点导纳矩阵；通过3.2节的Ward多端等值法在Matlab软件中计算得到4个直流接入点在不同谐波频率下的节点阻抗矩阵。

4.2 MIDC输电系统谐波相互影响分析

假设MIDC输电系统中交流电网不存在背景谐波，给定4个直流接入点注入交流侧的谐波电流源频谱如表1所示，可以得到在四回直流线路单独运行方式下各直流接入点的各次谐波电压有效值，根据第3节的介绍通过Matlab程序得到不同运行方式各直流接入点在不同谐波频率下的最小电压有效值和最大电压有效值，再由式(22)和式(23)计算得到不同运行方式下各直流接入点的绝对最小电压总谐波畸变率THDu-min和绝对最大电压总谐波畸变率THDu-max，那么各直流接入点的电压总谐波畸变率就界于THDu-min与THDu-max之间。

表1 谐波电流源频谱

表2给出了上海电网所包含的MIDC输电系统不同运行方式下的各直流接入点THDu-min和THDu-max，其运行方式包括以下几种：

(1)运行方式1～4表示MIDC输电系统中只有单回直流线路运行，包括华新站、枫泾站、南桥南站及奉贤站接入的直流线路分别单独运行；

(2)运行方式5～10表示MIDC输电系统中有两回直流线路同时运行，包括华新站-枫泾站、华新站-南桥南站、华新站-s奉贤站、枫泾站-南桥南站、枫泾站-奉贤站及南桥南站-奉贤站接入的直流线路同时运行；

(3)运行方式11～14表示MIDC输电系统中有三回直流线路同时运行，包括华新站-枫泾站-南桥南站、华新站-枫泾站-奉贤站、华新站-南桥南站-奉贤站及枫泾站-南桥南站-奉贤站接入的直流线路同时运行；

(4)运行方式15表示MIDC输电系统中所有直流线路同时运行。

多馈入交互作用因子(MIIF)是CIGREWGB4工作组提出的用于衡量多馈入直流输电系统中换流站之间相互作用强弱的指标[16]。由文献[17]可知:

(24)

由式(24)可以计算得到上海电网4个直流接入点的MIIF矩阵，如表3所示。

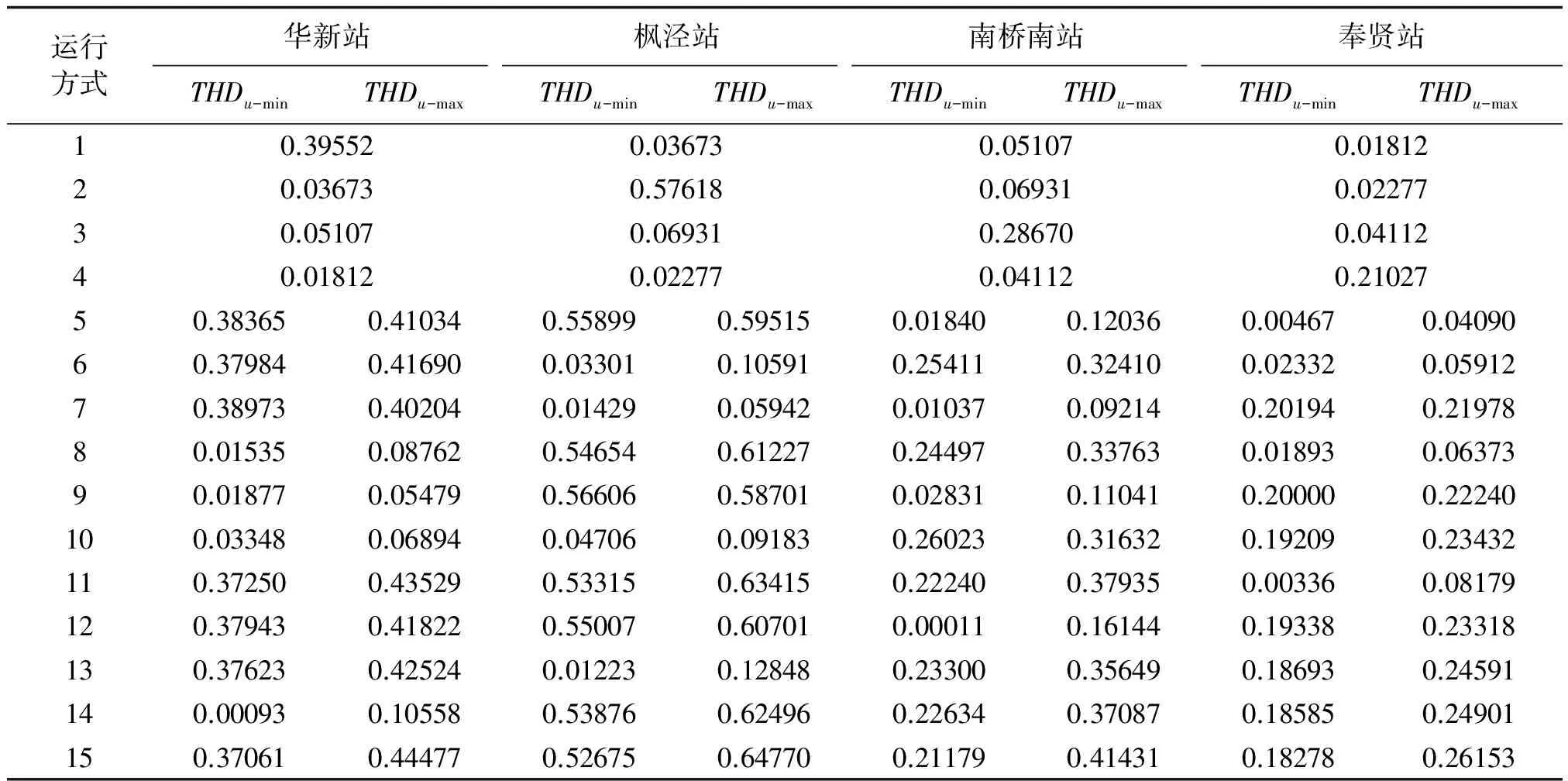
表2 MIDC输电系统在不同运行方式下各直流接入点的电压总谐波畸变率

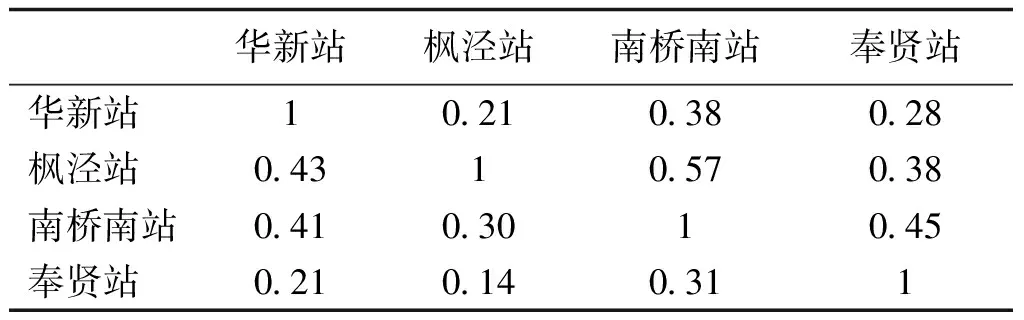
表3 MIDC输电系统各直流接入点间MIIF值

文献[15]指出，当多馈入直流输电系统各直流接入点间MIIFji<0.1时，各回直流间的谐波相互影响可以忽略不计；当0.1≤MIIFji≤1时，随着MIIF值的增大，各回直流间的谐波影响越大。表2中，运行方式1～4下各直流接入点的THDu的变化与表3中MIIF值的变化一致，所以用本文方法得到的各直流接入点的电压总谐波畸变率是符合实际情况的。由表2可以得出以下结论：

(1)在表1所示的谐波电流源频谱下，各直流接入点在MIDC输电系统不同运行方式下的电压总谐波畸变率都小于直流工程的限值1.75%；

(2)在各种运行方式下，各直流接入点的电压总谐波畸变率只有在接入自身的直流线路参与的运行方式下较大，其余情况均较小；

(3)对某回直流线路来说，在所有其参与运行的运行方式下，其接入点的电压总谐波畸变率的变化范围很小，且与其单独运行时的电压总谐波畸变率相近，所以可以认为其他直流线路的运行方式对其节点的电压总谐波畸变率影响很小，直流接入点电压的畸变主要受自身直流线路谐波的影响。

5 结论

本文首先给出了交流系统主要元件在谐波频率下的数学模型，利用Ward多端等值法推导出MIDC输电系统各直流接入点谐波频率下的节点导纳矩阵，进而可以得到节点谐波电压。之后，对上海电网500kV电压等级电网进行等值，通过计算得到上海电网包含的MIDC输电系统在不同运行方式下直流接入点的电压总谐波畸变率的范围。对计算结果分析发现，在不同运行方式下南桥南站的电压总谐波畸变率都远远小于直流工程的限值1.75%，华新站、枫泾站、南桥南站和奉贤站在自身接入的直流线路不运行的方式下，节点电压总谐波畸变率很小，只有在自身接入的直流线路运行的方式下，其节点电压总谐波畸变率才会较大，各直流接入点的电压总谐波畸变率变化范围很小，且与直流线路单独运行方式下相近。因此，对于上海地区多馈入直流输电系统，各直流接入点的电压总谐波畸变率主要受自身直流线路的影响，受其他线路的影响较小。

[1] 韩民晓，文俊，徐永海 (Han Minxiao，Wen Jun，Xu Yonghai). 高压直流输电 (High voltage direction current) [M]. 北京：机械工业出版社 (Beijing: China Machine Press)，2008.

[2] 梁继云 (Liang Jiyun). 高压直流输电中的谐波分析 (Harmonic analysis in high voltage direct current transmission system) [D]. 成都：西南交通大学(Chengdu: Southwest Jiaotong University)，2012.

[3] Nguyen Phuc Huy，韩民晓 (Han Minxiao). 直流阻容式电压互感器用于直流输电谐波电压测量的研究 (Study on application of DC resistive-capacitive voltage transformer in harmonic voltage measurement for HVDC) [J].电工电能新技术(Advanced Technology of Electrical Engineering and Energy)，2015，34(3)：54-60.

[4] 雷霄，王华伟，曾南超，等 (Lei Xiao, Wang Huawei， Zeng Nanchao, et al.). LCC 与VSC混联多端高压直流输电系统运行特性的仿真(Simulation research on operation characteristics of hybrid multi-terminal HVDC system with LCC and VSC) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy)，2013，32(2)：48-52.

[5] L Hu，R Yacamini. Calculation of harmonics and interharmonics HVDC schemes with low DC side impedance [J]. Generation, Transmission and Distribution, IEE Proceedings C，1993，140(6)：469-476.

[6] 颜伟，何宁 (Yan Wei， He Ning). 基于Ward等值的分布式潮流计算(Distributed power flow calculation based on the Ward equivalence method) [J].重庆大学学报(Journal of Chongqing University)，2006，29(11)：36-40.

[7] CIGRE Joint Task Force. AC system modeling for AC filter design - An overview of impedance modeling [J]. Electra，1996，164：131-151.

[8] Abu-Hashim R， Burch R， Chang G， et al. Test system harmonics modeling and simulation [J]. IEEE Transactions on Power Delivery， 1999，14(2)：579-587.

[9] 黄方能 (Huang Fangneng).天广交直流并联输电系统的谐波分析(The harmonic analysis of TIAN-GUANG AC/DC parallel transmission system) [D]. 南宁：广西大学 (Nanning: Guangxi University)，2001.

[10] Bonner A， Grebe T， Gunther E， et al. Modeling and simulation of the propagation of harmonics in electric power networks - I: Concepts models and simulation techniques [J]. IEEE Transactions on Power Delivery，1996，11(1)：452-465.

[11] 徐政，段慧 (Xu Zheng， Duan Hui). 全频段交直流系统等值与谐波计算程序的研发 (Program for AC system wide frequency range equivalence and harmonic calculation) [J]. 高电压技术 (High Voltage Engineering)，2008，34(6)：1131-1136.

[12] 段慧，肖海龙，徐政 (Duan Hui， Xiao Hailong， Xu Zheng). 基于潮流数据的输电线路谐波模型和电磁暂态模型研究 (Harmonic models and electromagnetic transient models of transmission lines based on power flow data) [J]. 华东电力 (East China Electric Power)，2007，35(9)：9-11.

[13] 段慧 (Duan Hui).交流系统谐波阻抗等值与背景谐波分析 (AC system harmonic impedance equivalence and background harmonic analysis)[D]. 杭州：浙江大学 (Hangzhou: Zhejiang University)，2008.

[14] 诸骏伟 (Zhu Junwei).电力系统分析 (Power system analysis) [M].北京：中国电力出版社 (Beijing: China Electric Power Press)，1995.

[15] 孙奇珍，蔡泽祥，朱林，等 (Sun Qizhen， Cai Zexiang， Zhu Lin， et al.). 互联电网的多端等值方法及其误差分析 (Multi-terminal equivalence method of interconnected power system and improvement based on its error analysis)[J]. 电网技术 (Power System Technology)，2008，32(23)：67-73.

[16] CIGRE Working Group B4.41．Systems with multiple DC infeed [R]．Paris：CIGRE，2008．

[17] 邵瑶，汤涌 (Shao Yao， Tang Yong). 采用多馈入交互作用因子判断高压直流系统换相失败的方法(A commutation failure detection method for HVDC system based on multi-infeed interaction factors) [J].中国电机工程学报 (Proceeding of the CSEE)，2012，32(4)：108-114.

Study on harmonic effects of multi-infeed HVDC systems

LIU Ting-ting1， WEN Jun1， QIAO Guang-yao2， FU Xi-xi1， ZHOU Sheng-jun2

(1. School of Electrical and Electronic Engineering, North China Electric Power University, Beijing 102206, China; 2. State Grid Smart Grid Research Institute, Beijing 102211, China)

Firstly, this paper introduces the harmonic mathematical model of the major components in the AC transmission system. The Ward multi-terminal equivalence method was used to get the node admittance matrix of the access points with DC link in the MIDC system. With the known current spectrum, the harmonic voltages of the access points with DC link can be calculated. At last theTHDuof the access points with DC link can be counted out. The 500kV voltage level network in Shanghai grid was made in equavalent based on the harmonic models. Then the ranges of the total harmonic distortion of voltage (THDu) for the access points with DC link were calculated. The conclusion based on the analysis is that the harmonic interaction between the DC access points of the multi-infeed DC system in Shanghai district is very weak. TheTHDuof the access point with DC link is mainly effected by the harmonics fed by the DC circuit linked to the access point.

multi-infeed DC; harmonic effects; mathematical model; Ward multi-terminal equivalence; total harmonic distortion of voltage

2015-03-22

刘婷婷(1989-)， 女， 河北籍， 硕士研究生， 研究方向为高压直流输电系统运行分析与规划的研究； 文 俊(1963-)， 女， 贵州籍， 教授， 硕士， 研究方向为高压直流输电系统运行分析与规划的研究。

TM714

A

1003-3076(2016)01-0042-06