基于TRIZ理论的单级功率因数校正电路拓扑分析

王尚宁， 丘东元， 张 波

(华南理工大学电力学院， 广东 广州 510640)

基于TRIZ理论的单级功率因数校正电路拓扑分析

王尚宁， 丘东元， 张 波

(华南理工大学电力学院， 广东 广州 510640)

发明问题创新理论(TRIZ)作为一种技术创新的方法论，已在诸多领域得到了广泛应用。本文尝试将TRIZ理论与电力电子变换器拓扑研究相结合，系统地提出一种电力电子变换器拓扑的构造方法。本文以单级功率因数校正电路为例，利用TRIZ理论中的冲突矩阵，深入分析了一些典型单级功率因数校正电路的拓扑构造原理，验证了TRIZ理论指导电力电子变换器拓扑设计的可行性和有效性，从而为构造性能更优越的功率因数校正电路提供了思路。

TRIZ； 冲突矩阵； 功率因数校正

1 引言

随着能源危机和全球环境的持续恶化，环保已经成为当今可持续发展的重要主题。由于电网也可以看作一种环境，故其同样面临着环保方面的问题。随着电力电子技术的快速发展，越来越多的电力电子设备接入电网，为负载提供所需的直流或交流电压，获得了显著的效益，但同时给电网带来了严重的谐波电流污染。最常用的二极管整流电路如图1所示，交流电压通过二极管整流，经电容滤波后供负载或后级电路使用。由于二极管仅在交流电压大于输出电压的时段内导通，造成了输入电流畸变，且整流电路的功率因数低。为此，需要采用功率因数校正(PFC)技术，提高电力电子设备的功率因数，降低其对电网的谐波污染。

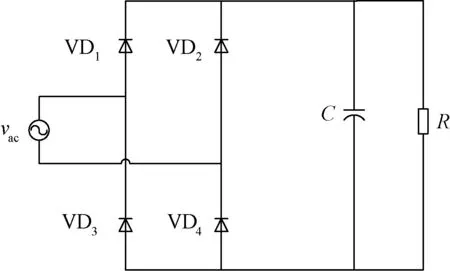
图1 二极管桥式整流电路Fig.1 Diode bridge rectifier circuit

功率因数校正电路可分为两级和单级两大类型。两级PFC含有两个变换器，其中前一级用于实现功率因数校正，而后一级用于实现对输出电压的快速调节。单级PFC则是将两级PFC中的前级电路和后级电路合二为一，共用一个开关管和一套控制电路，同时实现输入电流整形和输出电压调节，从而大大减小了器件的数量，降低了电路的成本。然而，现有的单级PFC电路或多或少还存在一些不足，如器件应力过高、控制复杂等，故高性能的单级PFC电路仍是当前的研究热点[1,2]。

发明问题创新理论(Teoriya Resheniya Izobreatatelskikh Zadatch，TRIZ)是前苏联发明家阿奇舒勒在分析了世界上近250万份高水平发明专利的基础上，于1946年提出的一套具有普遍适用性的发现问题并找到解决办法的发明理论。经过六十多年的发展，TRIZ已经发展为一套系统解决各类复杂问题的方法和工具[3,4]。一直以来，绝大部分电力电子变换器的拓扑结构都是设计者凭借自身的经验和灵感，并通过反复试验所得到的，至今尚未形成一套指导电力电子变换器拓扑构造的理论方法。因此，TRIZ的出现给电力电子变换器拓扑构造带来一个很好的启示。本文以单级功率因数校正电路为例，尝试用TRIZ理论分析该类电路的构造方法，以期提出一种构造电力电子变换器的系统方法。

2 TRIZ技术冲突解决原理

2.1 技术冲突

冲突是TRIZ理论的一个核心要素，表示隐藏在问题背后的固有矛盾。TRIZ理论认为创造性问题的解决至少要解决一对冲突[5]，而冲突主要分为两类，一类是技术冲突，一类是物理冲突。技术冲突指改进系统某一参数时，同时出现的不希望得到的结果，例如，提高汽车速度时需要耗费的燃料更多，速度和燃料就属于一个技术冲突。物理冲突则是针对物体的同一个参数提出两种完全相反的要求而产生的矛盾，例如，对于滤波电容来说，电容值越大滤波效果越好，但大电容往往意味着电容器的体积增大，此类矛盾属于物理冲突。本文在分析功率因数校正电路时，只涉及到技术冲突。

2.2 冲突矩阵

阿奇舒勒通过研究大量发明专利，分析、总结并提炼出了TRIZ理论中最重要的且具有普遍用途的40个发明原理，具体见附表1。同时，阿奇舒勒发现引起冲突的技术参数是有限的，所归纳出的39个通用技术参数见附表2。他将这39个技术参数构成一个39×39的矩阵，其中列代表冲突中改善的参数，行代表冲突中恶化的参数。那么，行列的交叉点就代表一个技术冲突，而解决该技术冲突的发明原理则用矩阵中的元素表示。矩阵元素或为空白，或为数字，其中数字代表发明原理的序号。完整的技术冲突矩阵可参见文献[6]。由此可见，该冲突矩阵将描述技术冲突的39个技术参数与可用于解决问题的40条发明原理建立了对应关系，很好地解决了设计过程中选择发明原理的难题。

2.3 解决实际问题的流程

冲突矩阵是TRIZ理论中实用率最高的工具。例如，若要设计一个具有省电模式却不影响照明效果的灯具，那么参考技术参数，可知需要改善的参数为20(静止物体的能量)，而恶化的参数为18(光照强度)。参考文献[6]，可知冲突矩阵中矩阵元素(20, 18)对应的发明原理序号是2、19、32和35，意味着可用于解决该技术冲突的发明原理为2-分离、19-周期性作用、32-改变颜色和35-参数变化。若采用周期性作用原理，可令该灯具间断性工作，即增加一个声电感应装置，就可以得到一个既具有省电模式又不影响照明效果的灯具[7]。

需要说明的是，实际遇到的问题并不能直接采用TRIZ发明原理来解决。因此，首先将实际问题转化为一般问题，也就是用TRIZ理论中的通用技术参数描述实际的技术冲突，进而构建冲突矩阵；其次，在冲突矩阵中找到解决该冲突的发明原理，这些原理提供了最有可能解决问题的思路；接着，根据系统的实际工作情况，过滤一些明显不适用的发明原理，得出一个或几个发明原理作为一般解；最后，结合相关领域的技术知识和实践经验将发明原理具体化，从而获得解决实际问题的方案，即特定解。上述利用冲突矩阵解决实际问题的流程如图2所示。

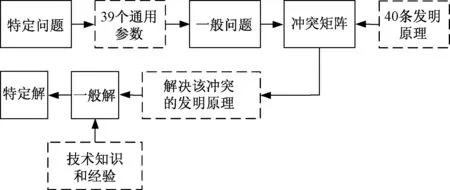
图2 冲突矩阵解决实际问题的流程图Fig.2 Diagram of conflict matrix to solve practical problems

3 TRIZ冲突矩阵与PFC电路

3.1 PFC电路的技术参数

若要利用冲突矩阵改进单级PFC电路的设计，按照图2，首先要将PFC电路中的技术参数用TRIZ的通用技术参数表示。如器件应力、有功功率、器件损耗等，可以直接用通用技术参数中的“应力、功率、能量损耗”等来描述；对于谐波含量，则可以用通用技术参数中的“物体产生的有害因素”来表示。经分析，用于描述单级PFC电路性能的常用技术参数共有8个，所对应的TRIZ通用技术参数见表1。由此可以构造出一个适用于单级PFC电路的8×8冲突矩阵，具体见表2。

表1 PFC电路的技术参数

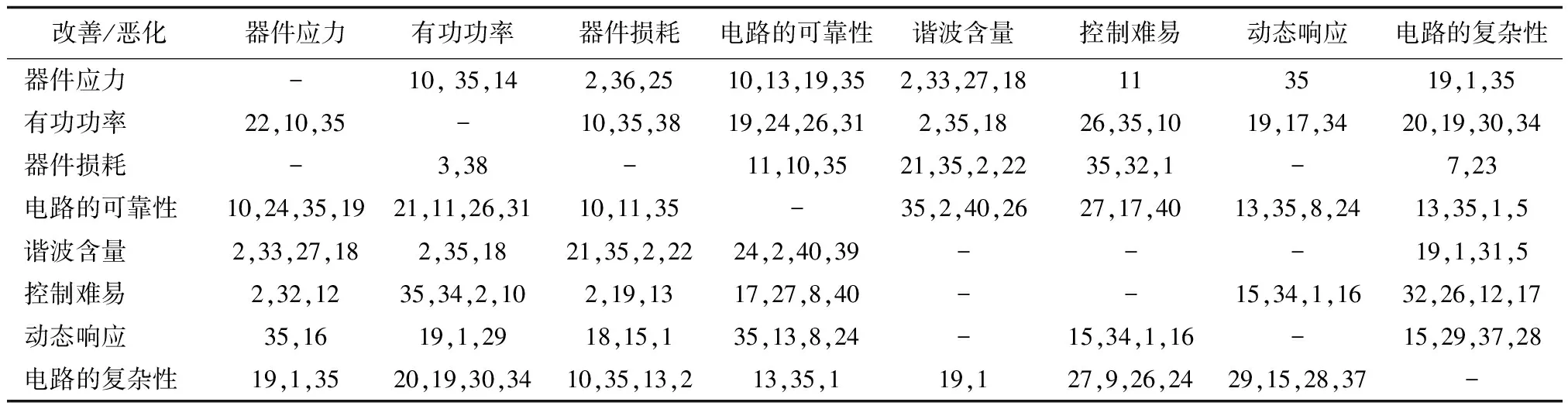
表2 PFC电路的冲突矩阵

3.2 PFC电路的改进过程

根据图2，在获得PFC电路的冲突矩阵后，需要确定电路的改造目标，即确定哪些技术参数需要改善，哪些技术参数可能恶化，才能在冲突矩阵中查找到解决该类冲突的发明原理。然后结合实际情况对PFC电路提出具体的改造方案，最后对新拓扑进行性能分析以及仿真和实验验证。若电路性能达到设计要求，那么所提出的改造方案可行；若未达到要求，则重新选择发明原理，设计改造方案，直到问题解决。

下面以一些典型的单级PFC电路为例，结合PFC电路的冲突矩阵，分析单级PFC电路的改进过程。

4 单级PFC电路的拓扑构造原理

4.1 无源PFC电路

PFC电路的基本形式是无源PFC电路，即采用无源元件构成的功率因数校正网络。对于图1所示的二极管桥式整流电路，如果采用无源PFC电路，那么欲改善的技术参数包括有功功率、谐波含量和电路的可靠性，但随之恶化的技术参数为器件损耗和电路的复杂性。参考表2，得到解决上述技术冲突的发明原理包括1-分割、11-预补偿、13-反向、19-周期性作用、20-有效作用的连续性、34-抛弃与修复、35-参数变化等。

若利用11-预补偿原理，可以在图1的二极管整流桥和滤波电容之间插入电感元件，如图3所示。利用电感抑制电流变化的特性，使输入电流变化平缓，由此提高功率因数。该基本无源PFC电路的优点是拓扑简单、无开关损耗、成本低、无需控制，但谐波含量仍然比较大，功率因数也不够高，且电感的体积较大。

图3 基本无源PFC电路Fig.3 Passive PFC circuit

若利用13-反向性原理，把电感放到整流桥之前，得到图4所示的电路[8]。与图3相比，该电路的电感电流不含直流分量，避免了电感磁心的饱和，从而提高了拓扑的可靠性。

图4 改进无源PFC电路Fig.4 Modified passive PFC circuit

利用20-有效作用的连续性原理，通过增加二极管的导通时间，也可以提高功率因数。若无源校正网络不采用电感元件，可将图1的滤波电容C改为由三个二极管和两个电容(C1、C2)组成的填谷式网络，如图5所示[8]。此时，只要输入电压的绝对值大于输出电压的一半，二极管就能导通，从而在不需要电感元件的情况下，提高功率因数。

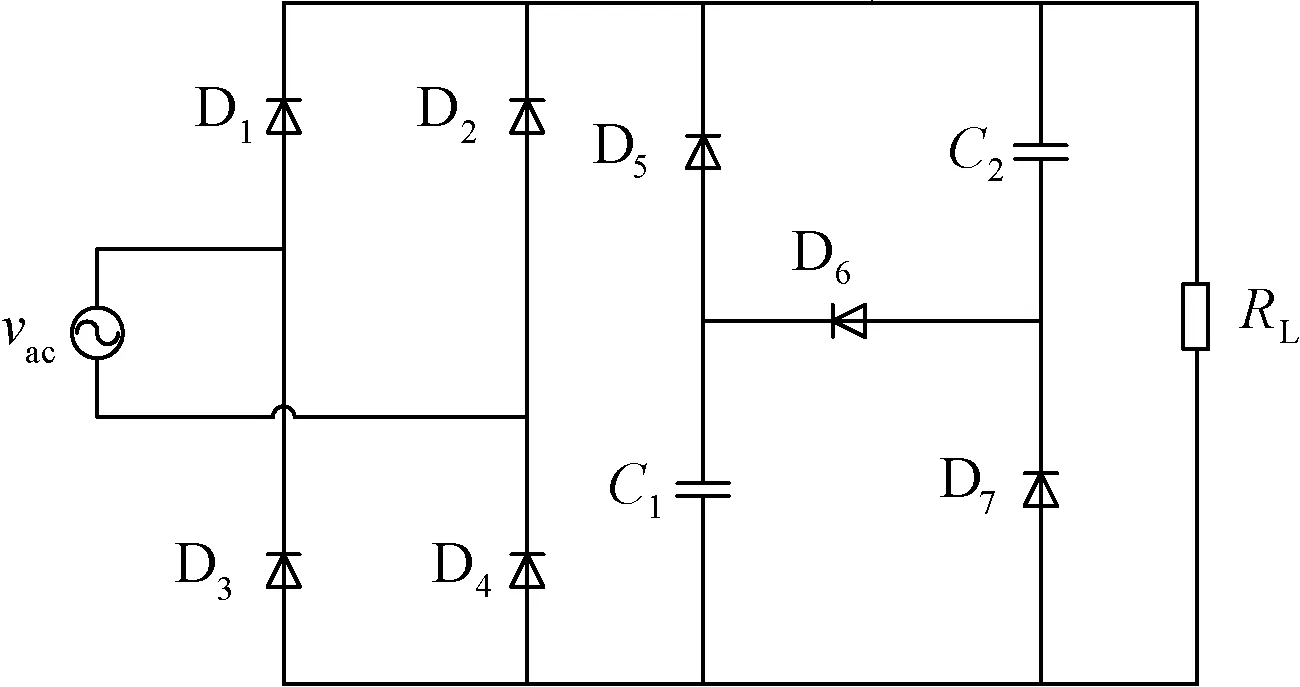
图5 填谷式PFC电路Fig.5 Valley type PFC circuit

由于图5所示的填谷式电路输出电压纹波较大，故可尝试利用34-抛弃与修复原理，对图5中的填谷网络进行局部改进。为了减小电容电压纹波，可以设法延缓电容充电和放电过程，即电容C1、C2分别串接一个电阻R1、R2，如图6所示[9]。经测试，此电路的功率因数比图5所示电路提高1～2个百分点。

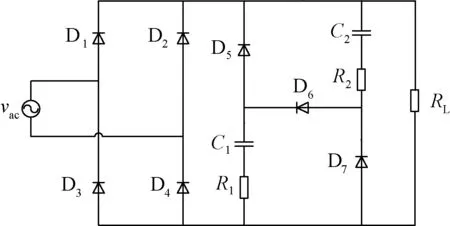
图6 改进型填谷式PFC电路Fig.6 Modified valley type PFC circuit

4.2 有源PFC电路

有源功率因数校正技术是一种强迫输入电流跟随输入电压，使输入电流正弦化，且与输入电压保持同相位的一种技术。在中小功率场合，图7所示的Boost PFC电路是目前广泛使用的一种有源功率因数校正电路。由于有源PFC电路含有控制电路，故欲改善的技术参数包括功率因数、谐波含量、器件损耗、动态响应以及拓扑的可靠性，而随之恶化的技术参数则是器件应力、控制复杂度以及电路的复杂性。参考表2，得到解决上述技术冲突的发明原理为1-分割、5-合并、10-预操性、13-反向性、19-周期性作用、20-有效作用的连续性和35-参数变化等。

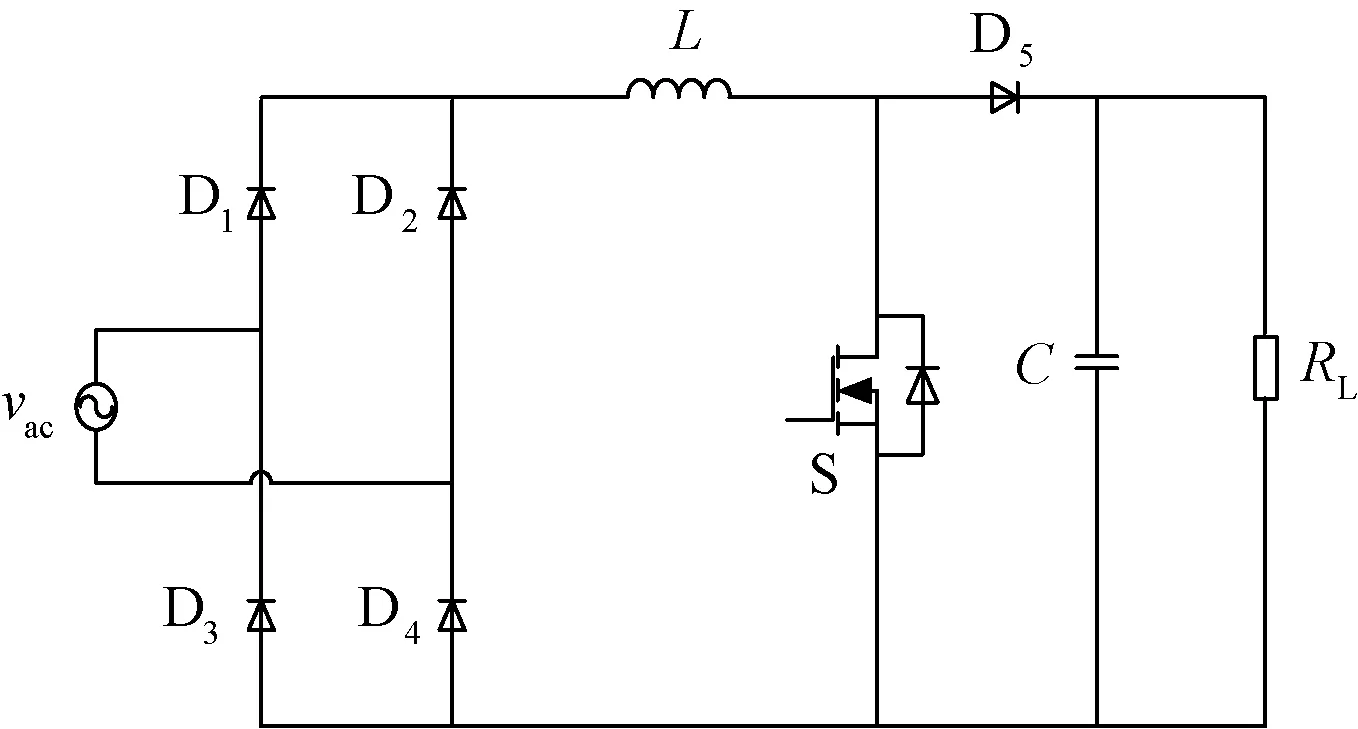
图7 传统Boost PFC 电路Fig.7 Traditional Boost PFC circuit

为了降低开关损耗，可利用19-周期性作用原理，用两个开关管S1和S2分别代替了图7整流桥中的两个二极管，得到的电路如图8所示，此电路被称为无桥PFC电路[10]。由于省略了整流桥，在电源电压每半个周期内，只有两个开关器件处于工作状态，比传统的Boost PFC电路少了一个二极管，通态损耗低，提高了效率。

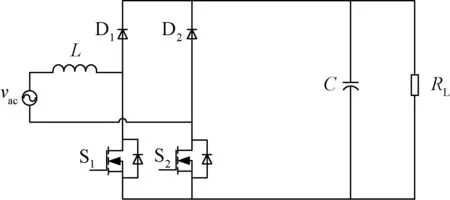
图8 无桥Boost PFC电路Fig.8 Bridgeless Boost PFC circuit

由于图8中电感直接与交流侧相连，对于高频信号来讲，电感相当于开路，PFC的输出与输入电源隔离而处于悬浮状态，因此电路的EMI问题比较严重，利用反向性原理把S2和D1互换位置，可得到新的无桥PFC拓扑，如图9所示[11]。分析电路可以发现，在输入电压正负半周期内，同样只有两个半导体器件处于工作状态，通态损耗低，且由于输入电源通过二极管D1和D2与输出端建立了联系，输出始终跟交流侧一端通过一个导通二极管相连，因此PFC输出不再处于浮动状态，共模干扰小。但在电感电流采样方面，此电路需要复杂的检测电路，同时两个开关管需要隔离驱动，驱动电路较为复杂。但由于该电路具有拓扑简单、器件利用率高、电磁干扰小等优点，在中低功率场合有较好的应用前景。

图9 改进无桥Boost PFC电路Fig.9 Modified bridgeless Boost PFC circuit

针对图9电路驱动电路复杂的问题，利用20-有效作用的连续性原理，借助二极管的续流作用，在图8中增加两个阳极共地的二极管D3和D4，而二极管的阴极分别与交流电源直接相连，如图10所示[12]。这样使输出端与电源建立了联系，同样减少了共模干扰。由于该电路的开关管S1和S2源极共地，所以可以共用一个驱动信号，驱动简单，通态损耗小。显然，该电路结合了图8和图9各自的优点。

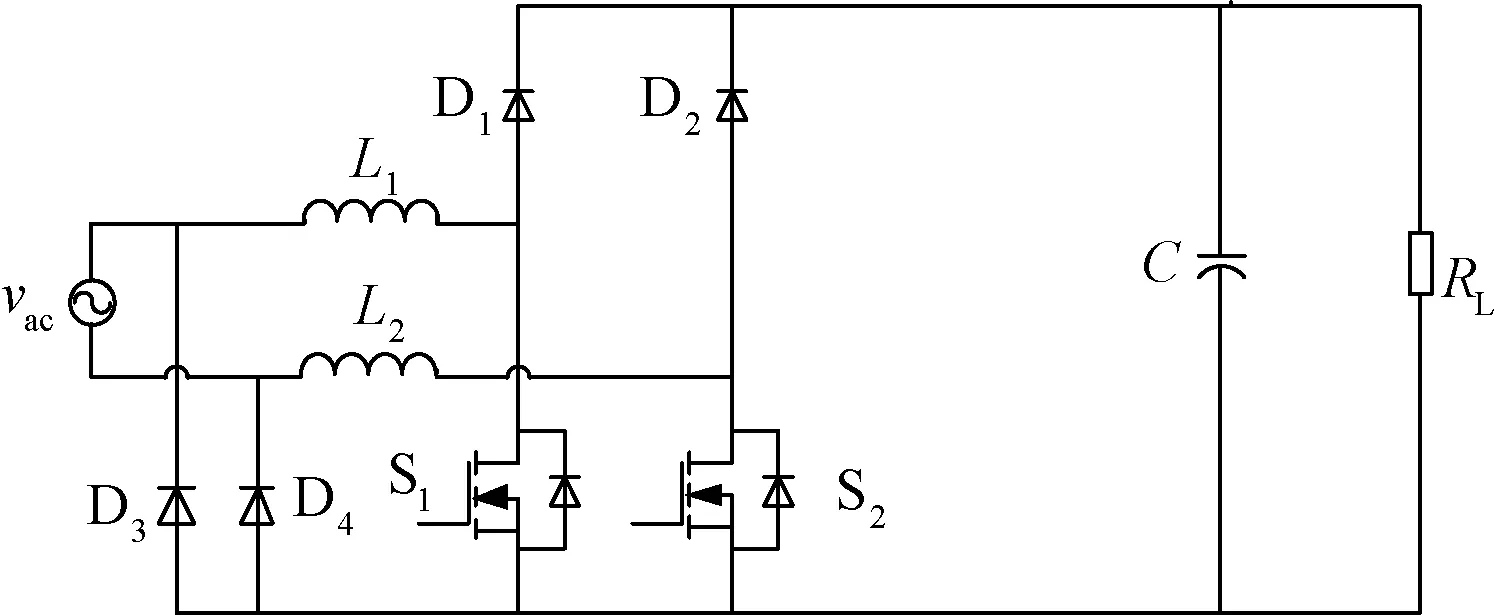
图10 双二极管式无桥PFC电路Fig.10 Double diode bridgeless Boost PFC circuit

传统Boost PFC主要用于输出电压高于输入电压的场合，当高电压输入时，往往需要具有升降压功能的Buck-Boost PFC。利用5-合并性这一发明原理，将传统的Buck与Boost前后合并起来，得到的电路如图11所示[13]。其中L既是Buck的输出电感也是Boost的输入电感，通过适当的方法可以提供一个直接从输入到输出的路径，有效解决了传统的Buck-Boost PFC器件应力高的问题。但需对该电路的两个开关管施加独立的驱动信号，使电路工作在两种状态，因此控制较为复杂。

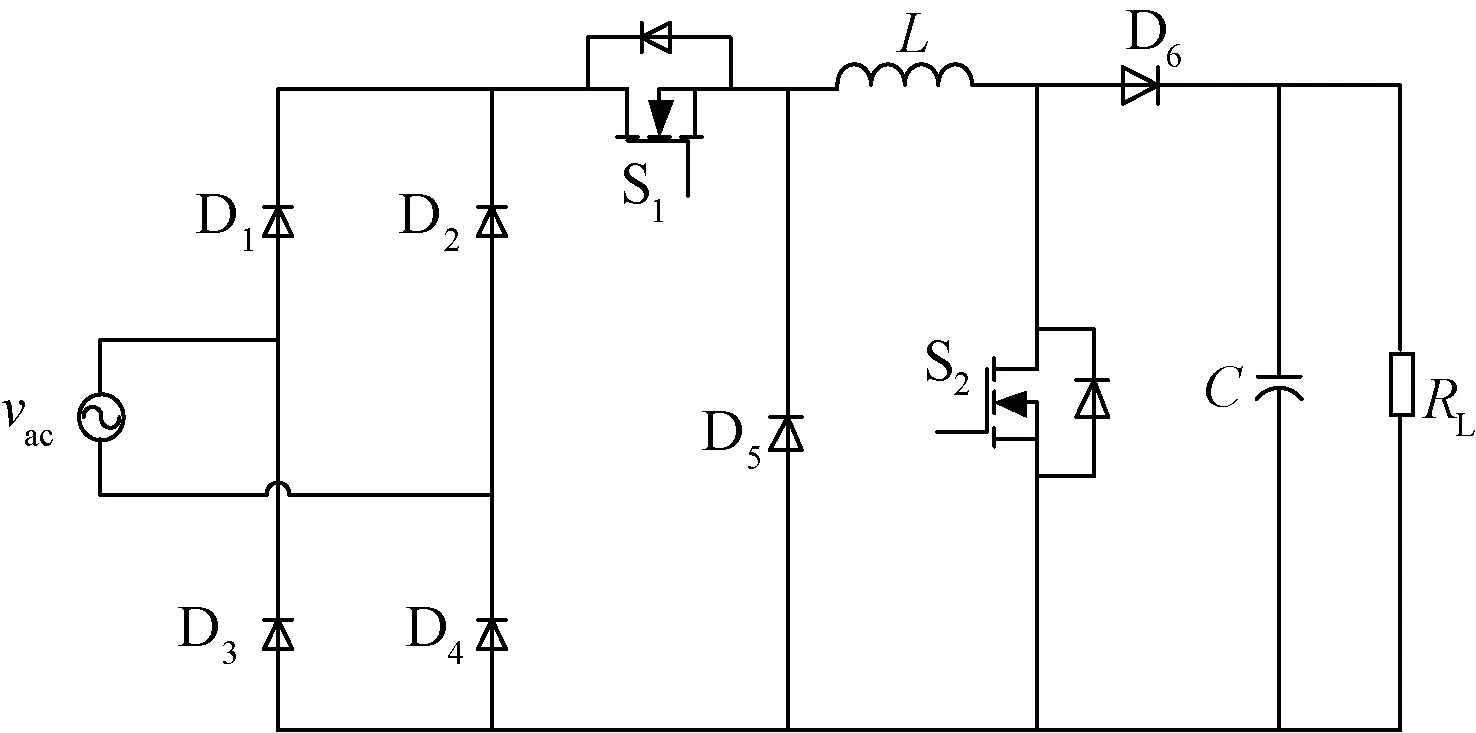
图11 级联式Buck-Boost PFC电路Fig.11 Cascading Buck-Boost PFC circuit

针对传统的Boost PFC电路器件应力高的问题，利用1-分割原理，可用两个Boost电路代替一个Boost电路完成相关功能，得到的电路被称为交错并联Boost PFC电路，如图12所示[14]。此电路的两个开关管占空比相同，交错工作，不仅可以降低器件的电流应力，还能有效降低输入电流纹波。

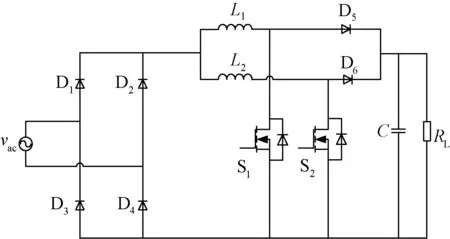
图12 交错并联Boost PFC电路Fig.12 Interleaved parallel Boost PFC circuit

综上分析可见，大部分单级PFC电路的拓扑构造思路都能通过分析技术冲突、根据发明原理而得到，由此证明了利用TRIZ冲突矩阵指导电力电子变换器拓扑设计的可行性。

5 结论

本文首次将TRIZ理论中的冲突矩阵应用于指导电力电子变换器的拓扑构造，并以一些典型的无源PFC电路和有源PFC电路为例，验证了该方法的有效性和可行性。初步研究成果表明，该方法与传统的依赖于设计者灵感和自身经验的设计方法不同，是一种具有系统性和理论性的拓扑设计方法，有助于促进电力电子变换器拓扑的发明与改进。

附录：

附表1 TRIZ的发明原理

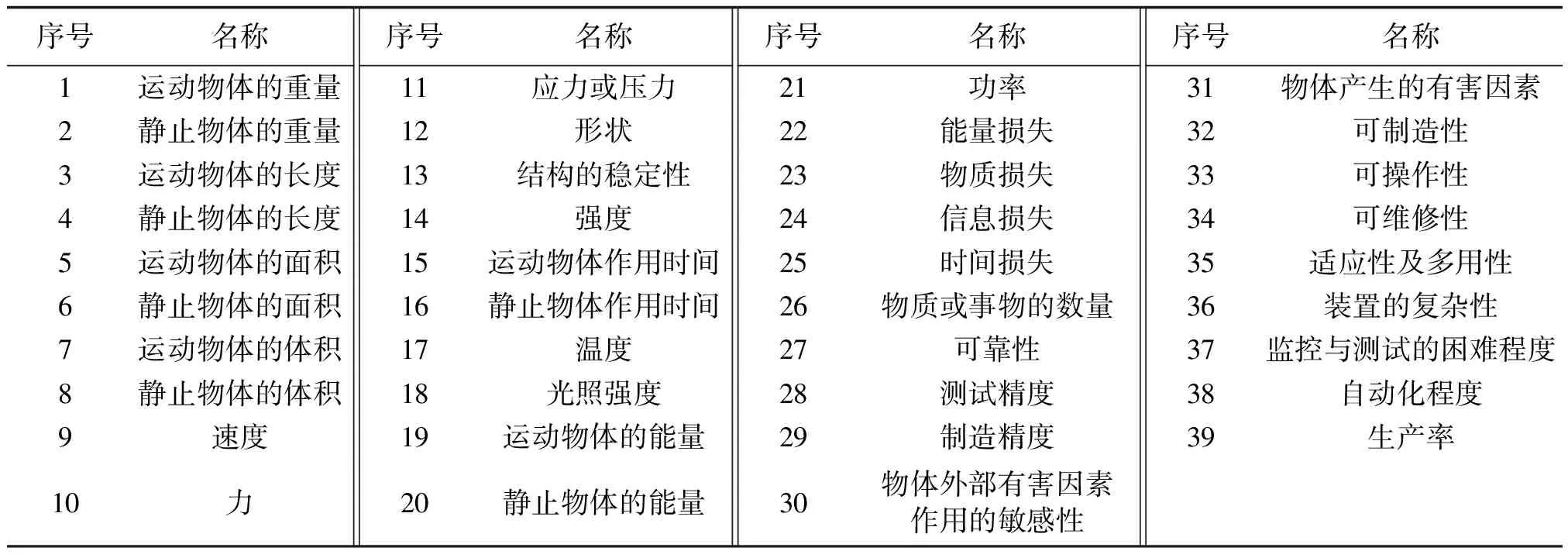
附表2 TRIZ的通用技术参数

[1] Zhang J, Jovanovic M M, Lee F C. Comparison between CCM single-stage and two-stage Boost PFC converters [A]. Applied Power Electronics Conference and Exposition [C]. 1999. 1: 335-341.

[2] 武杰，王春芳，刘茂盛 (Wu Jie, Wang Chunfang, Liu Maosheng).两级式高功率因数LED照明驱动电源的研究 (Research on two-stage LED power supply with high power factor) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering & Energy)，2014, 33(8): 73-76.

[3] Webb A. TRIZ: an inventive approach to invention [J]. Engineering Management Journal, 2002, 12(3): 117-124.

[4] Dwyer J. Problem solving the inventive way [J]. Engineering Management Journal, 2005, 15(2): 10-13.

[5] 檀润华 (Tan Runhua). TRIZ及应用技术创新过程与方法 (TRIZ and innovation process and methods applied technology) [M]. 北京：高等教育出版社(Beijing: Higher Education Press), 2010.

[6] 刘桂涛，袁春静，戴义贵 (Liu Guitao,Yuan Chunjing, Dai Yigui). TRIZ中技术矛盾解决矩阵的应用 (The application of technology contradiction solve matrix based on TRIZ) [J]. 机械设计与制造 (Machinery Dedign & Manufacture), 2007, 8(8): 63-65.

[7] 吕欣 (Lv Xin). 基于TRIZ理论中39矛盾矩阵与40创新原则的产品创新设计研究 (Research on product innovation design based on 39 contradictions matrices and 40 innovation principles of TRIZ) [J]. 包装工程 (Packaging Engineering), 2009, 30 (5): 211-213.

[8] Farcas C, Petreus D, Simion E, et al. A novel topology based on forward converter with passive power factor correction [A]. IEEE 29th International Spring Seminar on Electronics Technology (ISSE'06) [C]. 2006. 268-272.

[9] Itoh R, Ishizaka K. Single-phase sinusoidal convertor using MOSFETs [J]. IEE Proceedings B - Electric Power Applications, 1989, 136(5): 237-242.

[10] 林维明，洪翠，黄超，等 (Lin Weiming, Hong Cui, Huang Chao, et al.). 无桥PFC电路改进单周期控制的仿真与实验分析 (Analysis of a bridgeless PFC based on improved one-cycle-control) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering & Energy), 2013, 32(2): 21-23.

[11] Su B, Lu Z. An interleaved totem-pole Boost bridgeless rectifier with reduced reverse-recovery problems for power factor correction [J]. IEEE Transactions on Power Electronics, 2010, 25(6): 1406-1415.

[12] Jang Y, Jovanovic M M. A bridgeless PFC Boost rectifier with optimized magnetic utilization [J]. IEEE Transactions on Power Electronics, 2009, 24(1): 85-93.

[13] Mansouri M, Kaboli A, Hr S, et al. A review of single phase power factor correction AC-DC converters [A]. Clean Energy and Technology (CEAT) [C]. 2013. 389-394.

[14] Miwa B A, Otten D M, Schlecht M F. High efficiency power factor correction using interleaving techniques [A]. Proceedings of Applied Power Electronics Conference and Exposition (APEC'92) [C]. 1992. 557-568.

Topology analysis of single-stage power factor corrector based on TRIZ

WANG Shang-ning, QIU Dong-yuan, ZHANG Bo

(School of Electric Power, South China University of Technology, Guangzhou 510640, China)

As a methodology of technology innovation, TRIZ has been widely used in many fields. This paper attempts to combine TRIZ theory with power electronic converter topology research, and proposes a topology construction method for power converters systematically. Single-stage power factor corrector is used as an example in this paper, and some typical PFC circuits have been analyzed thoroughly by applying the conflict matrix in TRIZ, which proves the feasibility and effectiveness of the proposed method, and provides a guideline for designing the power factor corrector with better performance.

TRIZ; contradiction matrix; power factor correction (PFC)

2015-01-17

国家自然科学基金资助项目 (51277079)

王尚宁(1987-)， 男， 回族， 青海籍， 硕士研究生， 主要从事TRIZ理论在电力电子技术中的应用； 丘东元(1972-)， 女， 广东籍， 教授， 主要从事电力电子技术研究。

TM46

A

1003-3076(2016)01-0060-07