风力发电机自循环蒸发内冷系统并联回路两相流不稳定性的研究

李 旺， 王海峰， 顾国彪

(中国科学院电工研究所， 北京 100190)

风力发电机自循环蒸发内冷系统并联回路两相流不稳定性的研究

李 旺， 王海峰， 顾国彪

(中国科学院电工研究所， 北京 100190)

自循环蒸发内冷系统具有无泵自循环、冷却效率高、运行安全可靠和基本免维护等特点，非常适合在风力发电机中应用。由于风力发电机的特殊结构，其蒸发内冷系统需要采用具有一定垂直高度差的多通道并联结构。在这种结构中，各通道中的运行参数各不相同且相互耦合、相互影响，诱发系统的不稳定问题，对发电机的安全运行十分不利。本文基于一维均相模型，建立了多通道并联系统的模型，推导了其动阻力平衡方程组。基于平衡方程组，运用静态分岔理论及其DERPAR数值分析方法分析了三通道系统的静态稳定性及其参数效应，为风力发电机蒸发内冷系统的结构设计提供理论基础。

风力发电； 蒸发内冷； 倾斜并联通道； 两相流不稳定性； 静态分岔

1 引言

自循环蒸发内冷是一种安全高效的冷却方式，目前已成功应用于包括三峡700MW水轮发电机在内的多型发电机，并取得了非常好的运行效果。自循环蒸发内冷系统具有无泵自循环、冷却效率高、运行安全可靠和基本免维护等特点[1]。大型风力发电机安装高度高(一般为100m左右的塔台)，安装地点较为分散，这就要求发电机体积小、重量轻、运行安全可靠、维护量小。蒸发内冷式发电机恰能满足风力发电的特殊要求，利用风力发电机与水平方向有3°～5°夹角的特点，实现冷却系统的自循环[2]。

蒸发冷却技术在风力发电机上的应用，主要以直驱式风力发电机为主。直驱式风力发电机由于转速低，通常径长比较大，其定子直径较同等容量的双馈机型要大很多。目前而言，容量为5MW的直驱式风力发电机，其直径约为7～8m。在这种条件下应用蒸发内冷技术来冷却电机，位于定子槽内的倾斜空心导线相互之间就具有一定的垂直高度差[2]。多根具有一定垂直高度差的空心导线并联，由于高度差的存在，各个通道的运行情况存在差异，使得各通道的运行参数各不相同。而并联系统各通道共用一根回液管和集汽管，各通道参数相互耦合、相互影响，诱发系统的不稳定问题，对系统的安全稳定运行十分不利。因此，具有一定垂直高度差的多通道并联所引发的不稳定现象，是一个值得关注和研究的问题。

本文基于一维均相模型，推导了倾斜并联回路系统方程，运用静态分岔理论及其DERPAR数值分析方法[3]对并联系统的静态稳定性进行了分析，为风力发电机蒸发内冷系统的设计和运行提供理论参考。

2 自循环蒸发内冷系统并联回路模型

如图1所示，风力发电机蒸发内冷系统的并联回路主要由回液管、空心铜导体和集汽管组成。n根空心铜导体通过回液管和集汽管相连形成循环回路。图中各空心铜导体的长度均相等，设为L；各空心铜导体与水平面的夹角相等，设为θ；实际情况中，空心导体沿风力发电机定子圆周分布，导体间的高度差在1/4定子圆周内各不相同，假设第i根并联导体Li与第i+1根并联导体Li+1之间的高度差为Hi，且进出口两端的高度差相等。为便于分析，对系统作以下假定：

(1)冷凝器具有足够的冷却能力，确保其出口为单相液体，并可维持出口温度恒定，屏蔽了二次侧对一次系统的影响；

(2)空心导体通入电流，均匀加热，并且不计入过冷沸腾；

(3)两相段采用一维均相模型计算流动压降；

(4)不考虑沿程压力不同分布所引起的物性变化。

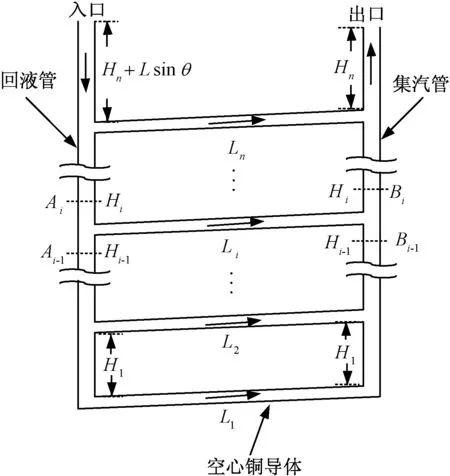
图1 风力发电机蒸发内冷系统并联回路系统Fig.1 Parallel loops system of IECS in wind turbine

根据以上假定，定义并联回路各段的参数，并推导并联系统的动阻力平衡方程组[4-6]。

2.1 并联回路系统参数

图1所示的系统中，每根空心铜导体加载的热负荷相等，均为Q；回液管和集汽管的等效水力直径相同，均为D1，且过流截面积为A1；各空心铜导体的等效水力直径相同，均为D2，且过流截面积为A2；空心铜导体入口介质(液相)密度均为ρin，运动粘度均为uin；第i条支路中介质的质量流量为mi。

2.1.1 空心导体段参数

式中，ρli为支路i中，蒸发点饱和压力对应的介质液相密度。

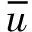
式中，uli为支路i中，蒸发点饱和压力对应的介质液相运动粘度。

空心导体i中单相段的长度Lli为：

式中，Hini为介质入口焓；Hsati为蒸发点饱和压力对应的介质焓值。

则两相段的长度Ltpi为：

空心导体i的出口干度xei为：

式中，Routi为出口处介质的汽化潜热。

空心导体i的出口焓汽率αi为：

式中，ρgi为支路i中，蒸发点饱和压力对应的介质液相密度。

空心导体i介质的出口密度ρtpi为：

空心导体i介质的出口运动粘度utpi为：

式中，ugi和uli分别为支路i中，蒸发点饱和压力对应的介质汽相和液相运动粘度。

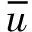
2.1.2 回液管中参数

回液管中为液体介质，忽略压力引起的物性变化，回液管各处介质的密度相等，即截面Ai处介质的密度为:

由质量守恒，有截面Ai处的介质质量流量为:

则介质的雷诺数为:

2.1.3 集汽管中参数

集汽管中为汽液两相介质，如图1所示，截面Bi处的介质的质量流量与截面Ai处相等，即：

截面Bi处介质的密度为:

干度(质量含汽率)为：

空泡率为：

运动粘度为：

雷诺数为:

2.2 系统的动力方程

从蒸发点之后，由于空心铜导体中汽液两相混合物的存在，介质的两相混合密度小于回液管中单相液体的密度，密度差在重力作用下形成了流动压头。故第i条支路的流动压头Pdrive(i)为：

(1)

2.3 系统的阻力方程

介质在流动通道内流动会受到阻力的作用产生压降。设回液管中Hi段的阻力压降为Pin(Hi)，集汽管中Hi段的阻力压降为Pout(Hi)；空心导体i中蒸发点前单相段的流动阻力压降为Pi(Ll)，蒸发点后两相段的流动压降为Pi(Ltp)；ΔPai为空心导体i中介质的两相加速压降。则第i条支路的流动阻力方程为：

(2)

式中

2.4 系统动阻力平衡方程

当第i条支路中介质的流动动力等于流动阻力时系统处于平衡状态。因此，第i条支路的动阻力平衡方程为：

(3)

由n条并联支路组成的系统的动阻力平衡方程组为：

(4)

将式(4)表示为：

(5)

式中，M=[m1,m2,…,mn]T为各支路的质量流量，Q=[Q1,Q2,…,Qn]T为各支路的加热功率。式(5)为n维非线性方程组，运用静态分岔理论及其DERPAR数值分析方法对该方程组进行数值求解，即可得到M随Q变化的静态分岔曲线。

3 实例分析

以n=3的三通道并联系统为例，其结构如图2所示，对系统的静态稳定性进行数值分析，其动阻力平衡非线性方程组为：

(6)

图2 三通道并联回路系统Fig.2 Three channels parallel loops system

系统主要参数为：H1=H2=0.3m，H3=2m，L=2m，入口欠热度为15K，D1=6.65mm，A1=34.68mm2，D2=4.43mm，A2=15.4mm2，θ=5°，且各支路的加热功率相等，设为Q。

根据式(6)，采用DERPAR数值分析方法，以质量流量m为状态变量，加热功率Q为分岔参数对系统进行静态分岔分析。分析结果如图3～图5所示。

图3 m1随Q变化的分岔曲线Fig.3 Bifurcation curve m1 changing with Q

图4 m2随Q变化的分岔曲线Fig.4 Bifurcation curve m2 changing with Q

图5 m3随Q变化的分岔曲线Fig.5 Bifurcation curve m3 changing with Q

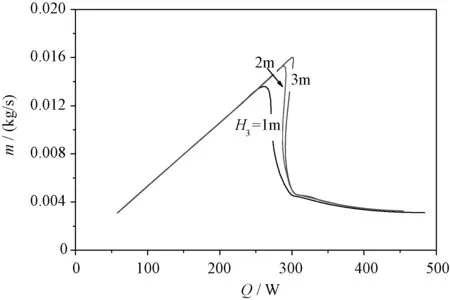
可以看出，在m1、m2、m3随Q变化的分岔中均存在一个非常小的多值区间，在此区间内系统存在三个平衡解，也就是说，在给定的热负荷Q下，系统有三种可能的运行状态，而系统到底在哪种状态下运行则取决于它的历史运行状况和外部扰动。在支路L2(或L3)中，随着Q的增大，支路的质量流量也增大，散热能力增强，当Q增大到Qmax2(Qmax3)时，该支路的稳定裕度[7]为0，此时任意微小的Q的增量都将导致系统质量流量m2(m3)的跃变，陡降到B2(B3)点的低质量流量状态。这种质量流量的跃变在蒸发内冷系统中是非常危险的，它将诱发沸腾危机，使发电机线圈温度猛升，甚至可能烧毁。而L1虽然也存在流量的突变点，但其质量流量降低值很小，不会引起沸腾危机。

为了避免沸腾危机的产生，将流量突降点所对应的Qmax定义为系统的散热极限[7,8]，L1、L2、L3的散热极限满足关系Qmax1

风力发电机自循环蒸发内冷系统的运行特性随系统运行参数、系统几何拓扑结构的不同而变化。研究风力发电机自循环蒸发内冷系统静态分岔现象的参数效应[9,10]，是研究风力发电机自循环蒸发内冷系统静态稳定性的一个重要内容。它对风力发电机自循环蒸发内冷系统的优化设计和安全运行有重要意义。对于各支路具有垂直高度差的多通道并联系统，垂直高度差所引起的系统不稳定现象，是一个值得研究的问题。

对图2所示系统，当保持H1=0.3m，H2=0.3m不变而改变H3时，各支路的最大质量流量和散热极限均随H3的增加而增大，如图6～图8所示。以m2为例，随着H3的增加，系统上升段提供了更大的驱动力使得介质的流速加快，在更高速度的流动状态下，内冷系统能够带走更多的热量。而当H3=1m时，虽然此时系统的极限散热能力相对较小，但各支路的静态分岔现象均消失，这意味着系统不会发生流量突变，稳定性增强。H3的增加虽然能够增大极限散热能力，但系统多值区间随之变大，稳定裕度变小，稳定性降低。因此，系统结构设计时应综合考虑各因素来选取H3的值。

图6 m1随Q变化的分岔曲线(H1=0.3m，H2=0.3m)Fig.6 Bifurcation curves m1 changing with Q(H1=0.3m，H2=0.3m)

图7 m2随Q变化的分岔曲线(H1=0.3m，H2=0.3m)Fig.7 Bifurcation curves m2 changing with Q(H1=0.3m，H2=0.3m)

图8 m3随Q变化的分岔曲线(H1=0.3m，H2=0.3m)Fig.8 Bifurcation curves m3 changing with Q(H1=0.3m，H2=0.3m)

保持H3=2m不变而改变H1、H2的取值，当H1、H2在小于0.5m的范围内变化时，m1、m2和m3的静态分岔曲线的变化趋势与保持H1=H2=0.3m而改变H3时的情况类似。而当H1和H2中有一个0.5m，或两者同时大于0.5m时，系统的静态分岔曲线会出现与上述情况迥异的多轨迹并行现象，且这种现象的出现与H3的大小无关。以H1=0.5m、H2=0.3m、H3=2m为例(其他参数不变)进行分析，结果如图9～图11所示。

图9 m1随Q变化的分岔曲线(H1=0.5m，H2=0.3m，H3=2m)Fig.9 Bifurcation curves m1 changing with Q(H1=0.5m，H2=0.3m，H3=2m)

图10 m2随Q变化的分岔曲线(H1=0.5m，H2=0.3m，H3=2m)Fig.10 Bifurcation curves m2 changing with Q(H1=0.5m，H2=0.3m，H3=2m)

图11 m3随Q变化的分岔曲线(H1=0.5m，H2=0.3m，H3=2m)Fig.11 Bifurcation curves m3 changing with Q(H1=0.5m，H2=0.3m，H3=2m)

可以看出，L1、L2和L3支路均出现了多条轨迹并行的分岔现象，各系统的多值区基本覆盖了整个热负荷Q的取值区间。三幅图中的1、2、3和4号运行轨迹分别对应，例如当L1运行于图9中的1号轨迹时，L2、L3则运行于图10和图11的1号轨迹。这种多轨迹并行的现象对支路L1的运行安全影响较小，因为其各条运行轨迹间的流量差很小，虽然在外部扰动下m1很容易产生波动，但其依然能够维持较大的值，不会发生局部过热。而L2、L3的运行轨迹间的流量差很大，且均存在低流量运行轨迹。由于各支路的平衡方程相互耦合，故m1的小范围波动会诱发m2、m3的大范围波动，甚至发生流量的大幅跌落，诱发沸腾危机，使得支路L2、L3的传热恶化，危及系统安全。

为了系统的运行安全，需要对并联回路结构进行合理的设计，避免出现上述容易诱发系统沸腾危机的不稳定现象。

4 结论

本文针对风力发电机蒸发内冷系统多支路并联通道，基于一维均相模型建立了并联通道流动不稳定性分析模型，推导了并联系统的动阻力平衡方程组。并联通道各支路互相耦合、互相影响，某一支路运行参数的改变会引起其他支路运行参数的改变。运用静态分岔理论及其DERPAR数值分析方法，对n=3的三通道并联系统的不稳定性及其参数效应进行了分析，并联通道之间的高度差对系统的稳定性有重要影响，当高度差超过一定数值时，并联支路出现多轨迹并行的分岔现象，对系统的安全运行十分不利。本文的研究能够为风力发电机蒸发内冷系统的结构设计提供理论基础。

[1] 阮琳(Ruan Lin).大型水轮发电机蒸发内冷系统的基础理论研究及自循环系统的仿真计算(The basic theory research of the inner evaporative cooling system for the large hydro-generator and the simulation of the CLSC system)[D].北京：中国科学院电工研究所(Beijing: Institute of Electrical Engineering，Chinese Academy of Sciences)，2004.

[2] 闫静(Yan Jing).风力发电机蒸发内冷系统中的两相流摩擦压降及不稳定性的基础研究(Study on the two-phase flow frictional pressure drop and instability of the evaporative inner cooling system)[D].北京：中国科学院电工研究所(Beijing: Institute of Electrical Engineering，Chinese Academy of Sciences)，2013.

[3] M 库比切克，M 马雷克(M Kubicek, M Marek).分岔理论和耗散结构的计算方法(Computational methods in bifurcation theory and dissipative structures)[M].北京：科学出版社(Beijing：Science Press)，1995.

[4] 鲁钟琪(Lu Zhongqi).两相流与沸腾传热(Two-phase flow and boiling heat transfer)[M].北京：清华大学出版社(Beijing: Tsinghua University Press)，2002.

[5] 徐济鋆，鲁钟琪(Xu Jijun, Lu Zhongqi).沸腾传热和气液两相流(Boiling heat transfer and gas-liquid two-phase flow)[M].北京：原子能出版社(Beijing: Atomic Energy Press)，2001.

[6] 陈听宽(Chen Tingkuan).两相流与传热研究(Two-phase and heat transfer)[M].西安：西安交通大学出版社(Xi’an：Xi’an Jiaotong University Press)，2004.

(，cont.onp.66)(，cont.fromp.29)

[7] 姚伟(Yao Wei).沸腾两相自然循环系统稳定性的试验与理论研究(Experimental and theoretical research on the instability mechanism of boiling two-phase natural circulation system)[D].上海: 上海交通大学(Shanghai：Shanghai Jiaotong University)，2000.

[8] 匡波，陈宏，徐继鋆, 等(Kuang Bo, Chen Hong, Xu Jijun, et al.).两相流自然循环流量漂移的分岔研究(Bifurcation investigation on flow excursion of two-phase natural circulation)[J].工程热物理学报(Journal of Engineering Thermophysics)，2005，26(1): 88-90.

[9] 佟立丽，姚伟，匡波, 等(Tong Lili, Yao Wei, Kuang Bo, et al.).两相自然循环系统的静态分岔特性机理分析(Mechanism analysis on static bifurcation of two-phase natural circulation)[J].核动力工程(Nuclear Power Engineering)，2001，22(3): 216-220.

[10] 王建军，杨星团，姜胜耀(Wang Jianjun, Yang Xingtuan, Jiang Shengyao).地干度自然循环两相流动系统的静态分岔特性(Bifurcation characteristic of two-phase flow in natural circulation system with low steam quality)[J].原子能科学技术(Atomic Energy Science and Technology)，2007, 41(2): 180-184.

Research of two phase flow instability in multiple parallel loops of natural circulation inner eaporative cooling system in wind turbines

LI Wang, WANG Hai-feng, GU Guo-biao

(Institute of Electrical Engineering, Chinese Academy of Sciences, Beijing 100190, China)

Natural circulation inner evaporative cooling system (IECS) has the advantage of self-circulation without pump, high cooling efficiency, safe and reliable operation, basically maintenance free, etc. It is very suitable for application in wind turbines. Due to the special structure of the wind turbine, its IECS needs to use parallel channels with different vertical heights. In this structure, each channel has different operation parameters, coupling with each other and influencing each other, induces instability problem of the system, and it is very detrimental for the safe operation of the generator. In this paper, based on one-dimensional homogeneous model, the model of multi-channel parallel system is established and the flow driving force and flow resistance balance equations are deduced. Based on the balance equations, static stability and its parameters effect of a three channel system are analyzed using the static bifurcation theory and DERPAR numerical analysis method. This can provide theoretical basis for the structure design of the IECS in wind turbines.

wind power generation; inner evaporative cooling; inclined parallel channels; two phase flow instability; static bifurcation

2014-11-21

国家自然科学基金资助项目(51177157)

李 旺(1987-)， 男， 广西籍， 博士研究生， 研究方向为风力发电机及其蒸发冷却技术； 王海峰(1966-)， 男， 河南籍， 研究员， 研究方向为可再生能源技术， 电机及其蒸发冷却技术。

TM315

A

1003-3076(2016)01-0024-06