关于河北省GDP问题的实证分析
杨茂梅
摘要:本文通过利用河北省1978-2012年GDP、CS(居民消费)、I(固定资产投资)的年度数据建立相关的经济时间序列的模型,通过对各变量序列的统计描述、单位根检验确定其相应特征,进行简单的趋势分解,建立VAR、VEC模型,并对模型进行检验得出结论。
关键词:时间序列;趋势分解;VAR模型;VEC模型
中图分类号:F127 文献识别码:A 文章编号:1001-828X(2016)010-000-02
一、引言
GDP是一个可以用来体现出某个地区的生活水平、经济水平以及发展水平的经济指标。GDP是考虑到了经济总量的影响。GDP的值一方面可以给某地区的领导人提供一定的依据来制定经济目标;一方面也可以让这些地区能够采取正确的方法,从而来解决在这些地区因为经济发展水平增长从而产生的一连串的社会问题。
这篇文章用河北省1978年到2012年的GDP的资料作为依据,用到固定资产投资I以及居民消费CS来作为解释变量,从而建立趋势分解、VAR和VEC模型,阐述了GDP增长的变化的规律,而且,还用这个规律来进行预测以及分析,为河北省未来的经济发展提供相应的依据。
二、数据描述
(一)原始数据
本文选取了河北省1978-2012年的GDP、居民消费(CS)和固定资产投资(I)的年度数据,用eviews对GDP、CS、I三个序列进行描述统计量,可以得到GDP、CS和I三个序列的标准差分别是7335.102、2060.237、4042.046,说明这三个序列之间的差异和离散程度很大。也就表明1978-2012这34年间河北省的经济发展速度十分迅猛。
三、实证分析
(一)VAR模型
所谓的VAR模型,也就是把模型中的全部的当期变量用来对全部的变量的无数个滞后变量来进行回归。对于一个含有了f个变量的p阶向量的自回归的模型,可以设为 VAR(p)。这样的模型的公式是:
在这个模型里面,Yt表示的是k维内生变量向量,p用来表示的是滞后的阶数;而则用来表示的是k维的扰动向量;Xt用来表示的是d维的外生变量的向量,维的矩阵,以及维的矩阵B则用来表示的是要被估计的系数的矩阵;最后用来表示的是这个样本的个数。
1.平稳性检验
在计量的角度对时间序列的数据作分析的时候,一开始就要把各个变量用来做平稳性检验,这样做就能够避免掉因为直接对非平稳的时间序列做回归而很有可能产生的误差。用ARIMA模型做平稳性检验可以得到:GDP、CS、I是二阶单整的。
2.Granger因果检验
本文通过运用Eviews7.0软件对GDP、CS和I序列进行了Granger因果检验,可以得出结论:由相伴概率得知I是GDP的格兰杰原因,GDP也是I的格兰杰原因;GDP是CS的格兰杰原因,CS也是GDP的格兰杰原因;I是CS的格兰杰原因,CS不是I的格兰杰原因。由此可以看出河北省的GDP、CS和I三个宏观经济变量之间是紧密联系的。
3.VAR模型的构建
这篇文章把CS和I看做是内生变量,同时各个变量是平稳的,此外这些变量间还存在着因果交叉的关系,因此,可以建立无约束的模型并且能够利用脉冲响应预测方差分解来阐述经济增长的变化情况。第一步是要确定这个模型的滞后阶数,关于滞后阶数的选取方法,这篇文章使用的是从一般再到特殊的方法 :从比较大的滞后阶开始 ,可以先利用t值检验来对滞后的阶数作出调整;或者是运用SC准则以及AIC信息准则来确定,用这个方法,要选择的阶数应该是使得SC和AIC的值越小的才越好。然而这篇文章把这两种方法综合在一起,通过试验, 就选了滞后阶数2 ,它的 AIC和SC的值比较小,然后建立了VAR模型。
4.脉冲响应分析
所谓的脉冲响应函数也就是能够用来衡量随机扰动项的一个标准差冲击对于其它的变量现在以及未来的取值的一个影响轨迹,这个函数可以很直白地体现出各个变量之间的动态交互作用以及这些变量之间的效应。
根据脉冲响应函数可以得到:GDP对其自身一个标准差冲击的影响立即就有反应,且在第三期后大致呈增加趋势;其对CS的一个标准差冲击在第一期为0,但随着时间的推移,其反应变化不大;在GDP对I的响应图中,可以看出GDP对I在这10期中存在负响应,且随着时间的推移,反应大体呈现下降趋势但变化幅度不大;而CS对GDP的一个标准差的冲击在缓慢的增加且在第一期就有反应;其对自身的一个标准差的冲击比较小,大体趋于稳定;而在CS对I的响应图中,看出在1-2期呈下降,第三期开始上升,第四期达到最高点,此后大致呈现下降趋势;I对GDP的一个标准差冲击在第一期就有反应,随着时间的推移,其反应伴随着小幅的波动;I对CS的一个标准差冲击呈现负响应,但在这10期中呈现平缓态势;最后在I对其自身的一个标准差冲击在第一期就有反应,随着时间的变化,其反应由最初的正响应变为最后的负响应。
根据以上检验,能够建立VAR模型,并且可以运用脉冲响应预测方差分解来阐述经济增长的变化情况。
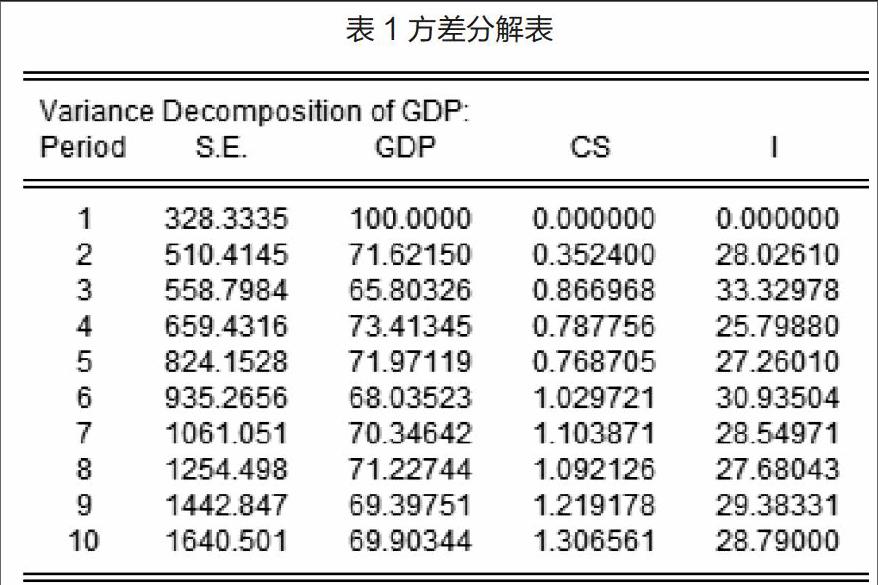
5.方差分解
从表1可以看出,河北省的GDP增长在第1期只受其自身波动冲击影响,从第2期开始,就有来源于它自己的扰动反复波动,一直到第9期开始,方差分解结果才平稳下来。通过长时间来看,GDP增长的变化当中,有69%左右的机会是通过它自己来决定的。消费这部分对GDP的影响,是从第2期才开始的,这部分的影响最终也只是保持在了1%左右,也就是说,消费对河北省的经济增长并没有起到很大的拉动作用。但是,固定资产投资的波动对河北省的经济增长却有着特别明显的影响,这部分的影响最终保持在了28%左右的水平,也就是说河北省的经济增长与投资的关系将会日益密切。
(二)VEC模型及建模过程
1.协整检验
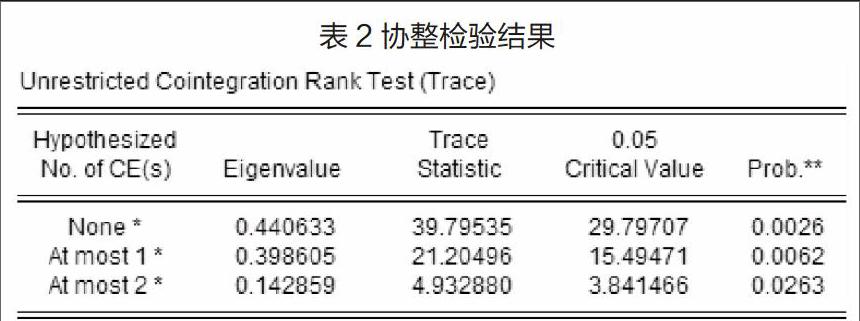
基于VECM的估计和Johansen协整检验需要系统里的每一个变量是同阶单整过程。为了不发生“伪回归”的问题,在进行协整分析的前面先进行变量的平稳性分析。且在上面ARIMA模型的构建中我们已经对GDP、CS、I序列进行了平稳性检验,而检验的结果显示:变量CS,I,GDP最开始的数据和CS,I,GDP的一阶差分序列在10%的置信水平下都不是平稳的,但是CS,I,GDP经过二阶差分之后全部在10%的置信水平上是平稳的,也就是变量GDP,CS,I都全部是二阶单整序列, 这样它们几个变量之间具备协整检验的必要条件。本文采用Johansen协整检验法,得到检验结果,如表2所示:
由表2各相伴概率可知:GDP、CS、I之间存在两个以上协整关系。
2.VEC模型的估计
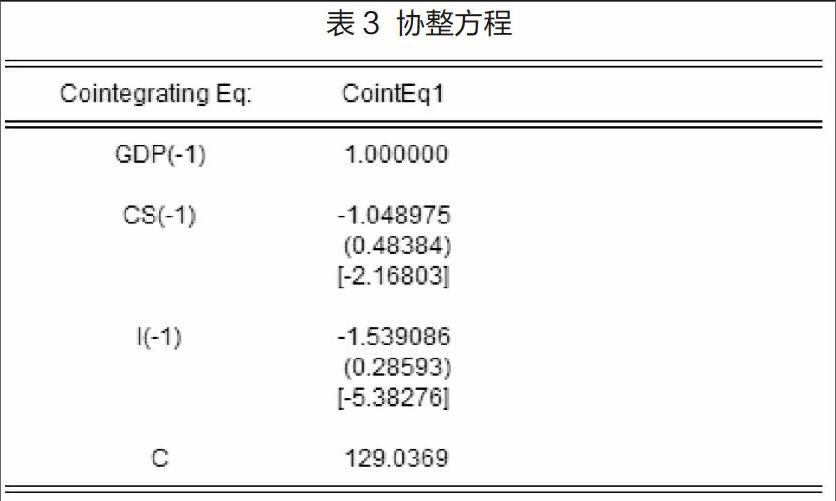
在进行序列的协整检验、平稳性检验、确定VAR模型的滞后阶数后,通过对初始数据的形态分析,得到VEC模型的估计,估计结果如下
从此误差方程中可知:GDP每增加1个单位,GDP(-1)对它的影响是-1.52个单位,GDP(-2)对它的影响是1.07个单位;CS(-1)对GDP的影响是0.06个单位,CS(-2)对GDP的影响是-1.91个单位;I(-1)对GDP的影响是1.60个单位,I(-2)对GDP的影响是-2.23个单位。
四、结论
这篇文章是依照1978-2012年河北省的GDP统计资料,变成平稳序列是通过差分,针对河北省GDP的非平稳特征,然后建立河北省每人平均GDP时间序列的VAR和VEC模型。依据模型能知道,河北省GDP的增长与上期增长有相关的联系,与随机误差也有关系。由实证分析结果可以看出来VAR和VEC模型可以比较好的解决河北省每人平均GDP的预测问题和估计,预测精度较高。
综上所述,可以得到相应的结论:GDP、居民消费和固定资产投资三者之间是紧密联系的,三者存在协整关系。所以河北省在发展经济的时候要注意协调发展,制定政策时应考虑到消费与投资之间的关系,统筹规划,合理发展。
参考文献:
[1]高铁梅.计量经济分析方法与建模—EViews应用及实例.清华大学出版社,2009(05).
[2]任英华.EViews应用实验教程.湖南大学出版社,2008(07).
[3]李惠.ARIMA模型在我国全社会固定资产投资预测中的应用.黑龙江对外经贸,2010(7).
[4]邓莉,段冬梅,陆凤彬,许伟,杨翠红,王寿阳.我国猪肉消费量集成预测—基于ARIMA、VAR和VEA模型的实证.系统工程理论与实践.2012(04).
[5]冯雅丽.河北省人均GDP时间序列的建立与预测.中国商界,2010(3).
[6]赵长城,李惠.基于VAR模型的河北省经济增长波动分析,华北金融,2010(6).

