基于VaR—GARCH模型对交易型货币基金风险的实证研究
郑荻+牛慧+万冬瑾
摘要:本文分别在正态分布、t分布和GED分布三种不同的假设条件下通过GACRH(1,1)模型,对我国市场中现有的七只交易型货币基金收益率的波动性进行分析,并建立一个基于GARCH模型的VaR计算方法,对我国交易型货币基金的风险进行估计,再利用失败概率对VaR估计结果的准确性进行返回检验,最终发现基于GED分布下的VaR-GARCH模型更能真实地反映基金风险。
关键词:交易型货币基金;VaR-GARCH模型;风险度量
中图分类号:F822 文献识别码:A 文章编号:1001-828X(2016)010-000-04
一、引言
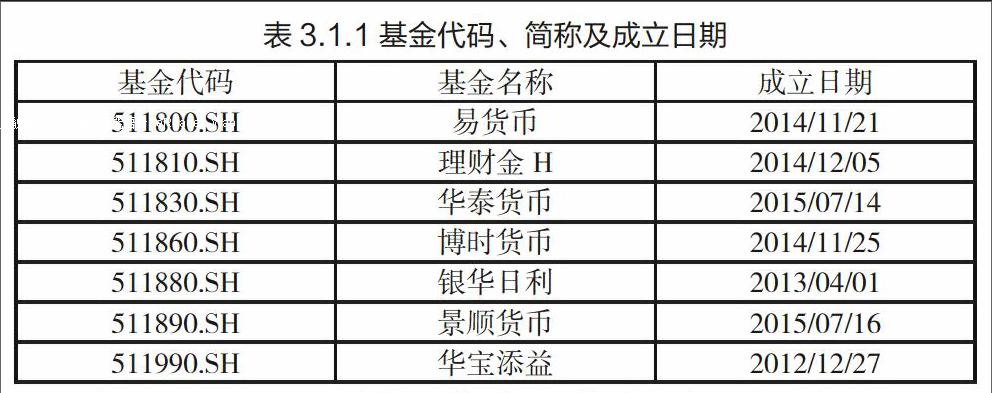
自2012年我国首只交易型货币基金华宝添益成立以后,目前我国市场共有七只交易型货币基金。交易型货币基金是近年来金融市场上的创新产品,相关领域的研究尚不完善,随着交易型货币基金的迅速发展,其投资风险日益显露,因此建立合适的模型对交易型货币基金的风险进行度量十分必要。
在对基金风险的研究中,目前多数学者用基金收益率的波动来刻画基金风险。在研究波动规律时,通常用方差或者标准差数据进行计量,自回归条件异方差模型最早在1982年由外国学者Engle提出,后经Bollerslev发展形成GACRH模型,现被广泛应用于波动性的分析与预测,特别是用在金融时间序列的研究中。
二、研究方法
在分析金融时间序列时,通常会遇到数列的方差具有时变性的现象,即在某段时间内收益率的波动在某一特征值附近成群出现,在统计学角度称该序列存在异方差现象。为了更好地体现出这种波动集聚效应,广义自回归条件异方差(GARCH)模型被广泛应用于金融时间序列数据的分析。本文拟采用VaR模型来刻画交易型货币基金的投资风险,考虑到收益率时间序列可能存在尖峰厚尾和波动成群等现象,在计算VaR过的程中,本文将引入GARCH模型,建立一个基于GARCH模型的VaR计算方法,从而对我国交易型货币基金的风险进行更为准确的估计。
1.在险价值(VaR)模型
在险价值(VaR)是指:在一定的置信水平(α)下,某一风险资产或组合在未来特定时期内可能发生的最大损失。当收益率r服从Z分布时,其计算公式为VaR=Zα,其中Zα 表示在α置信水平下的分位点,表示t时刻收益率的标准差。VaR的含义为该风险资产或组合在置信水平α下可能出现的最大损失。
2.广义自回归条件异方差(GARCH)模型
式中:是解释变量向量,是系数向量。式(2.2.1)为均值方程,将均值表示成一个带有扰动项的外生变量的函数。式(2.2.2)为条件方差方程,称作条件方差,是以之前信息为基础的向前预测方差,式(2.2.2)表示的含义是在时刻t状况下,的条件方差由t-1时刻下的残差平方(即ACRH项)和上一期方差的预测值(即GARCH项)决定。
三、实证部分
1.样本选取
通过对样本数据的初步观察与分析,本文在我国现有的7只交易型货币基金中,选取成立时间相对较早,数据完善程度相对较高,具有代表性的[511880.SH]银华日利为例,对其在2013/04/01至2016/03/31的每日单位净值和计算出的日收益率数据进行深入分析,建立一个能较好地反映交易型货币基金收益率波动规律的模型。
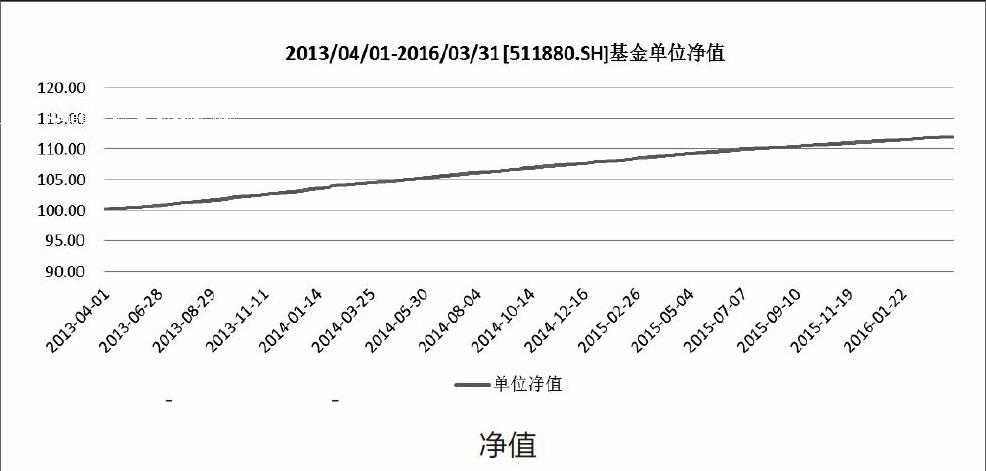
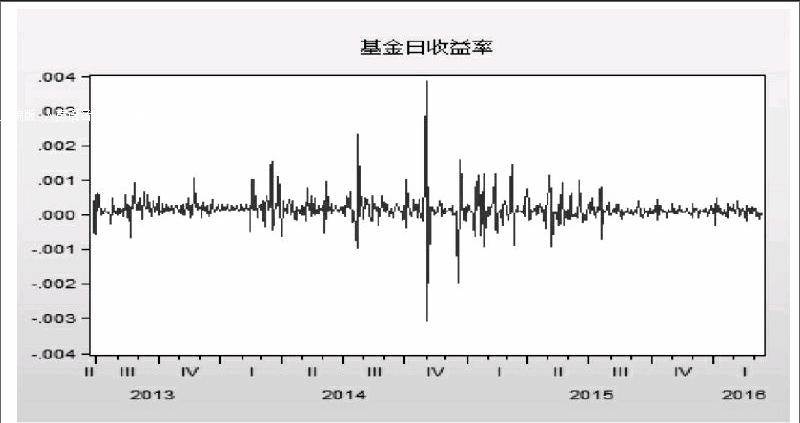
图3.1.1为基金[511880.SH]银华日利自成立以来的日单位净值折线图(数据来源于Wind数据库),从图中可以看出,从2013年4月1日到2016年3月31日期间,这只交易型货币基金日单位净值总体呈平稳增长状态。进一步地,通过式3.1.1计算得到交易型货币基金的日收益率时间序列,如图3.1.2所示。
2.平稳性检验及相关性分析
由于GACRH模型只适用于平稳序列建模,因此本文对[511880.SH]银华日利的日收益率进行单位根检验(ADF检验),检验结果如表3.2.1所示:
从表3.2.2可知,[511880.SH]银华日利的收益率的ADF值为-17.4262,均小于各显著性水平下的临界值,由此可以认为该收益率序列是平稳的。
3.最小二乘法估计
为了减少估计误差,在估计时对{511880.SH收益率}序列进行自然对数处理,即将序列{}作为因变量进行估计。由于基金收益率序列用一种随机游走模型描述,结合本例进行估计的基本形式为:
该方程的统计量显著,R2=0.999881说明拟合的程度也很好,但是观察图3.3.1:回归方程的残差图,可以观察到序列{}存在波动“成群”的现象,即波动集聚性,波动在一段较长的时间里非常小,如2013年7月与2016年1月;在其他一下较长的时间内非常大,如2014年6月与2015年4月。上述现象说明误差项可能存在条件异方差性。
从自相关系数和偏自相关系数可以看出,AC和PAC的系数显著不为0,而且Q统计量非常显著,可以说明式(3.3.2)的残差序列存在一阶ARCH效应。
4.GARCH(1,1)模型的拟合结果及检验
由于式(3.3.2)存在明显的ARCH效应,因此利用GARCH(1,1)模型对式(3.3.1)重新进行估计,为了更准确地描述时间序列的尾部特征,本文对GARCH模型中的扰动项的分布进行假设,假设残差序列分别服从正态分布、t分布和广义误差分布(GED)三种不同分布的,其估计结果如下:
通过对比GARCH(1,1)估计结果和最小二乘估计结果可以发现,在残差项服从上述三种分布的假设下,方差方程中的ARCH项和GARCH项的系数都是显著的,并且对数似然值相比于最小二乘估计都有所增加,同时AIC和SC值也均有所减小,说明GARCH(1,1)模型能够更好的拟合数据。再对这个方程进行条件异方差的ARCH-LM检验,得到的残差序列在滞后p=3时的相伴概率为0.93,不拒绝原假设,认为该残值序列不存在ARCH效应,说明利用GARCH(1,1)模型消除了残差序列的条件异方差性。
5.基于GARCH(1,1)模型的VaR估计
为研究我国市场上的交易型货币基金,本文通过对表3.1.1中的七只基金的日收益率数据进行整理分析发现, 基金收益率的标准差普遍偏高,具有较大的波动性。基金收益率序列的峰度在3.59到4.26之间,并在5%显著性水平下均大于3,说明基金收益率分布具有尖峰厚尾特征。
本文进一步地对上述7只交易型货币基金的日收益率进行平稳性检验(ADF检验),统计结果显示,基金日收益率序列是平稳的,随后又对基金日收益率序列进行自相关性检验,根据自相关函数值与偏自相关函数值以及序列的LM检验统计量结果可以看出,基金日收益率之间不存在自相关性。在此之后,本文对样本基金日收益率进行ARCH-LM检验,从F统计量及其概率可知基金收益的波动具有条件异方差性,即表中的七只基金的日收益率序列存在ARCH效应检验。
由于收益率序列通常具有尖峰厚尾特征,且存在条件异方差性,因此本文将建立一个基于GARCH(1,1)模型的VaR计算方法,在残差序列分别服从正态分布、t分布和广义误差分布(GED)三种不同分布的假设下,对我国交易型货币基金的风险进行估计。
利用式3.4.1、式3.4.2、式3.4.3、式3.4.4、式3.4.5和式3.4.6求出七只交易型货币基金分别在95%置信水平或99%置信水平下,当残差项分别服从标准正态分布、t分布和广义误差分布(GED)三种假设时的VaRt值,再求每只基金的VaRt值的算数平均,得到每只基金的VaR值,其计算结果如表3.5.1所示。
6.基于GARCH模型的VaR估计值的返回检验
VaR是反映基金投资风险的估计值,其测量结果的准确程度受到估计模型的影响,本文分别在三种假设分布下对基金收益率进行基于GARCH模型的VaR估计,因此需对不同模型所估计的结果分别进行返回检验,即检验三种假设分布下VaR的测量结果对实际损失的覆盖程度。
本文采用失败频率检验法对VaR估计值进行返回检验。观察七只基金的收益率序列和其在三种假设分布下计算的VaR均值,若损失超过VaR值则记为失败,若损失小于VaR值则记为成功。设实际检验天数为N,失败天数为n,失败频率为P=n/N。在95%和99%的置信水平下,分别比较其七只交易型货币基金在第t日的VaRt值与不同模型估计的VaR进行比较,得到每只基金返回检验的失败概率,结果如表3.6.1所示。
从表3.6.1可以看出,在95%的置信水平下,当残差序列服从正态分布和广义误差分布假设时,基于GARCH(1,1)模型计算出的VaR估计值的失败概率较低,均通过了返回检验,而t分布假设下基于GARCH(1,1)模型计算的VaR估计值则失败次数较多,有一只基金未能通过返回检验。在99%的置信水平下,只有当残差序列服从GED分布假设时,基于GARCH(1,1)模型计算出的VaR通过了返回检验,而正态分布假设和t分布假设下计算出的VaR估计值则失败概率较大,分别有一只和三只基金未能通过返回检验。
四、结论
通过上述分析和研究,本文发现交易型货币基金的收益率序列呈现尖峰厚尾特征,序列还存在波动集聚性,且由于基金收益率的残差序列具有条件异方差性,运用GARCH(1,1)模型能够消除残差序列的ARCH效应,更好的拟合数据。
本文通过运用基于GARCH(1,1)的VaR计算模型,对我国七只交易型货币基金的风险进行估计。通过观察估计值的返回检验结果可以发现:由于交易型货币基金的收益率序列具有尖峰厚尾特征,假设残差项服从标准正态分布时建立的GARCH(1,1)模型不足以刻画其尖峰厚尾特征,导致对金融资产风险的估计出现较大的误差;此外,当假设残差项服从t分布时所建立的GARCH(1,1)模型,虽然能够较好拟合数据,但利用其算出的VaR值低估了实际损失,返回检验的失败概率相对较高;相比之下,基于GED分布假设下建立的GARCH(1,1)模型具有较好的拟合效果,同时其所计算出的VaR值还能够比较真实地反映基金风险。
参考文献:
[1]高铁梅.计量经济分析方法与建模—EViews应用及实例[M].北京:清华大学出版社,2009,5.
[2]陈权宝,连娟.对我国开放式基金风险的实证研究—基于GARCH模型的VaR方法[J].经济问题,2008(9).
[3]周泽炯.基于VaR-GARCH模型对证券投资基金风险的实证研究[A].华东经济管理,2009,02.

