一个向量恒等式与三角形“四心”的联系
2016-05-24 07:55浙江省杭州高级中学310003
中学数学研究(江西) 2016年5期
浙江省杭州高级中学 (310003) 王 蕾
一个向量恒等式与三角形“四心”的联系
浙江省杭州高级中学(310003)王蕾
近几年在各个省份的竞赛中频繁出现与三角形“四心”(即外心,内心,垂心,重心)有关的向量问题,笔者出于兴趣,对三角形中的“四心”结合各个省的竞赛题做了对比研究,发现文中性质所提的这个一般性结论非常实用,于是笔者就竞赛题,说说这一结论的妙用,供大家参考.
一、一个向量恒等式

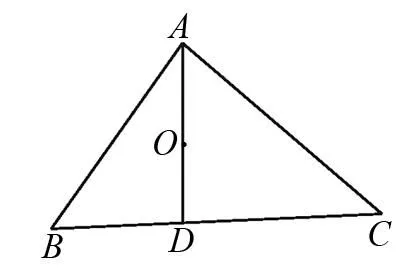
图1
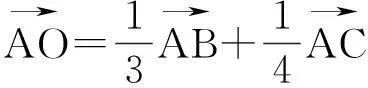
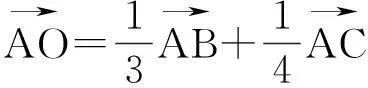
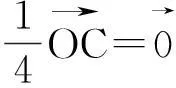
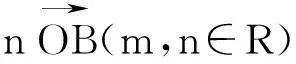
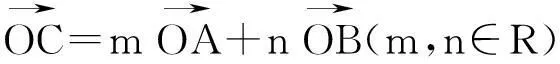

二、三角形“四心”的向量表示
上述恒等式中的O点是任意的,如果取三角形的”四心“这样的特殊点,会有怎样的结果呢?
推论1若O是三角形ΔABC的外心,则
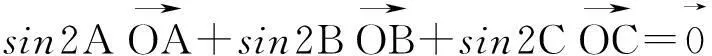


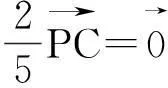
推论2若O是三角形ΔABC的内心,则

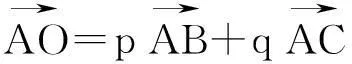
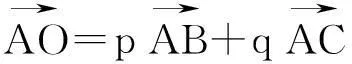
推论3若O是三角形ΔABC的垂心,则

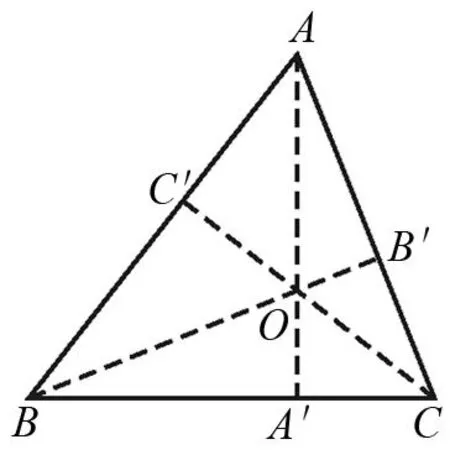
图2
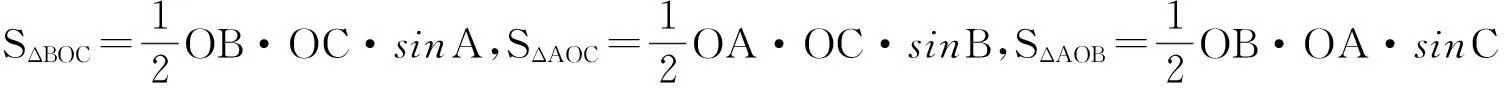
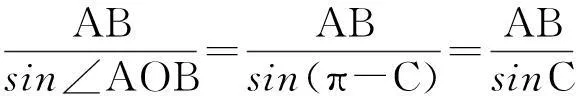


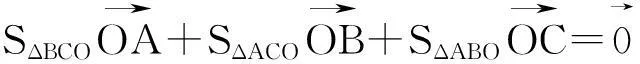
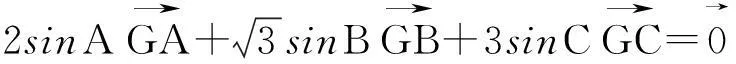
三、向量恒等式在空间的推广
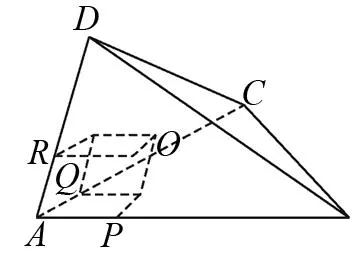
图3

猜你喜欢
中学生数理化·高一版(2023年2期)2023-03-23
歌海(2022年4期)2022-11-27
应用数学(2022年4期)2022-10-31
中等数学(2022年4期)2022-08-29
中等数学(2020年7期)2020-11-26
中等数学(2020年4期)2020-08-24
中等数学(2019年5期)2019-08-30
新闻前哨(2016年11期)2016-12-07
新教育时代·教师版(2016年27期)2016-12-06

