基于分支定界法的电能表计量电路容差设计方法

李求洋 ，李 新 ，王淑娟

（1.哈尔滨工业大学 电气工程及自动化学院，黑龙江 哈尔滨 150001；2.哈尔滨建成集团有限公司，黑龙江 哈尔滨 150030）

0 引言

为了适应现代化电网自动化管理的需要，智能电能表成为了电能计量表计的主流，直接关系着用户和电力企业之间的经济效益［1-2］。在智能电能表出厂检定时，通常不使用硬件方法调试计量误差，而是采用软件方法进行调整［3-4］。这种方法虽然调整了受检定的电能表测试精度，但并没有从根本上保证批量智能电能表的精度一致性要求。

近几年，批次智能电能表误差一致性问题渐渐得到重视，并且智能电能表相关国标也对其加以定义［5］。文献［6-7］通过定性地分析智能电能表误差的来源，给出了关键元器件的选型精度。文献［8］采用试验的方法，验证了相比传统模拟电路测量法，通过电子式电流传感器测量的负载电流误差一致性明显提高。然而，通过早期设计实现对误差一致性控制的文献还不多见。因此，有必要由设计入手保证测量精度，形成智能电能表的误差一致性设计方法。

容差设计是解决批次产品一致性问题的有效方法。但容差设计方法的研究对象多为机械结构，针对电子系统的设计优化仍停留在照搬用于机械结构的优化方法。然而，电子系统与机械结构的设计有所不同，如机械零件的制造公差在加工工艺允许范围内可以任意连续选定，而电子元器件的选型通常是按照等级离散划分。对于设计变量离散的情况，现阶段的容差设计方法主要通过不断地“试凑”来进行公差分配，设计效率依赖于设计人员的技术经验［9-10］。尤其对于包含大量元器件、计量质量要求高的智能电能表的设计优化，现有的容差设计方法更难以实现。

为此，本文提出以批次单相智能电能表的误差特性一致性为研究对象，首先分析单相智能电能表的结构和计量原理，其次基于整数规划思想通过分支定界算法实现对离散设计变量的优化，然后根据“成本-公差”模型建立容差设计优化方程，最后对单相智能电能表计量电路进行容差设计，并对优化方案进行分析。

1 单相智能电能表的工作原理

1.1 系统结构

智能电能表是指以智能芯片为核心，具有电功率计量、计时、计费、与上位机通信、用电管理等功能的电子式电能表。图1为典型单相电能表的硬件设计框图，包括计量系统和单片机处理系统两部分。其中计量部分是电能表计量准确性的关键部分，通常由电阻分压网络完成电压信号取样，微型电流互感器完成电流信号取样，取样后的电压、电流信号传送入计量芯片，并由内部乘法器转换为功率信号以脉冲信号通过SPI总线输出到单片机中。单片机处理系统对采样到的脉冲信号进行累加运算，同时根据设定的费率实现计量，实现各个部件协调控制等功能。

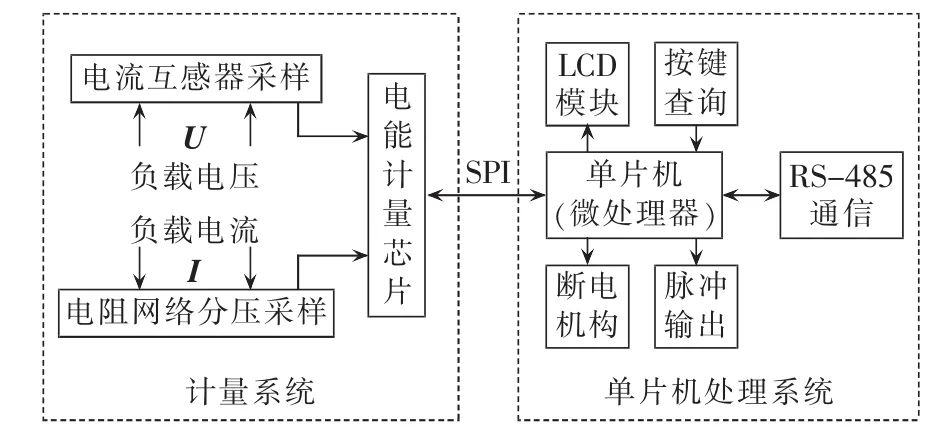
图1 电能表系统结构Fig.1 System structure of electrical energy meter

1.2 电能计量原理

电能计量主要把输入的动态电压和电流信号相乘，得到功率随着时间变化的信息，假设电流、电压为余弦函数，并存在相位差φ，则功率为：

经过变换，瞬时功率p（t）可以转化为：

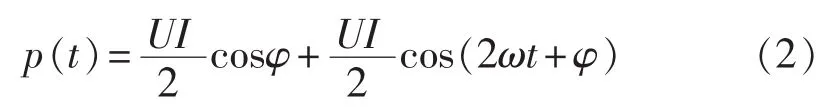
理想的瞬时功率信号只包括直流部分和频率为2ω的交流部分，而前者是电能表测量的首要对象。通过对电流、电压信号高精度采样和A/D转换后，电流、电压信号通过数字乘法器得到瞬时功率信号p（t）；再经一个截止频率很低的低通滤波器，将直流部分输送到数字/频率转换模块，转换为频率与能量消耗大小成正比的脉冲信号，并用计数器完成计量。

基本误差是考核电能表计量性能的最基本性能指标，电能表的等级指数一般是按基本误差确定的，通常用相对误差形式表示基本误差［11-12］。相对误差等于允许的绝对误差与输入量的约定真值的百分比，即：

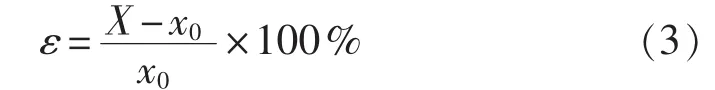
其中，X是测量值，x0是与X相对应的约定真值。对于智能电能表而言，这里的测量值即为功率值。设某批次共n只智能电能表，它们的计量误差为ε=（ε1，ε2，…，εn），则该批次产品的误差变化范围可表示为：

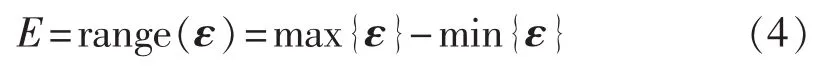
2 容差设计算法实现

2.1 “成本-公差”模型

智能电能表的质量要求和制造成本存在冲突，而元器件精度（偏差水平）是影响这一冲突的关键因素［13］。Chase等提出了制造成本与元器件偏差水平的关系曲线，曲线表明盲目地提高元器件的精度等级，虽然保证了产品质量，但产品的制造成本会随之增加，造成产品失去市场竞争力［14］；而随意地降低元器件精度等级要求，虽降低了成本，但会影响产品质量，导致批次产品性能分散大，用户投诉率上升［15］。制造成本由于其对容差影响的直观性，常被作为评定设计公差分配合理性的主要准则［16］。通常选用满足产品质量要求的最低成本进行公差分配，即容差设计。

半个多世纪以来，国内外学者提出了十余种“成本-公差”模型，例如倒数模型、指数模型、线性指数组合模型等，如表1所示。“成本-公差”模型的选择依照实际情况，通过获得有关成本和公差的经验数据，并在此基础之上选取合适的近似模型拟合得到。

表1 常见的“成本-公差”模型Table 1 General “cost-tolerance” models

2.2 分支定界算法

分支定界法（Branch-and-Bound）是 20世纪 60年代由Land、Doig和Dakin等人提出的可用于求解整数线性规划ILP（Integer Linear Programming）的算法。该算法通过放宽ILP问题的约束条件，得到其松弛问题，即线性规划 LP（Linear Programing）问题［17］。如果松弛问题的最优解保证每一个变量均为整数，则原问题得到解决。如果松弛问题的最优解中某个变量的值不为整数，则需要进一步地进行“分支”和“定界”运算。分支定界算法流程描述如下。

a.求解相应的LP问题，得到初始最优解x0，有最优目标函数值 f0=f（x0）。

b.若LP的初始最优解中任意变量为整数，它也是ILP的最优解，则优化停止。

c.若LP的初始最优解不符合ILP中的整数条件，记最终的ILP最优目标函数值为f，即有f≥f0。

d.在x0中任选一个不符合整数条件的变量xi，设其值为 li。 加入 2 个约束条件 xi≤［li］和 xi≥［li］+1（［li］是不超过li的最大整数），将原 LP问题分解为LP1和LP2 2个后继问题，并分别进行求解得到最优解 x1、x2和最优目标函数值 f1、f2。

e.对于2个后继问题中满足整数条件的最优解（若无可跳过此步骤），选取相应目标函数值最小者作为新的上界fU，即有fU≥f≥f0。

f.对于2个后继问题中不满足整数条件的最优解（若无可跳过此步骤），选取相应目标函数最小者作为新的下界fL代替f0，即有f≥fL=f0。

g.对不满足整数条件的分支，重复步骤d—f，比较各分支的最优目标函数值与fU的大小，若f≥fU，则剪掉这一支，进入步骤h；若f≤fU，且不符合整数条件，则重复步骤g。

h.最终的目标函数值f*=fU，对应的x*为最优解。

2.3 整数规划问题转换

分支定界算法针对的是ILP问题，而容差设计问题需经过相应的转换才能应用分支定界方法。转换过程包括2个方面：一方面是将各元器件的容差归一为正整数，另一方面是将非线性的目标函数和约束条件用近似模型近似。设n个元器件中的第m个元器件存在 k 个精度等级，用 m1、m2、…、mk表示，按照绝对值由小到大顺序，依次对应正整数1、2、…、k。以2个电阻R1、R2为例，假设它们的阻值为1kΩ，R1具有 3 个等级的容差分别是±10 Ω、±20 Ω、± 50 Ω，R2具有2个等级的容差分别是±10 Ω 和±50 Ω，则R1和R2的容差转化为正整数的形式如图2所示。设Ztol表示包含每个元器件精度等级信息的正整数矩阵，例如当 Ztol=［3，1］时，代表此刻 R1、R2的容差分别选择为±50 Ω、±10 Ω。

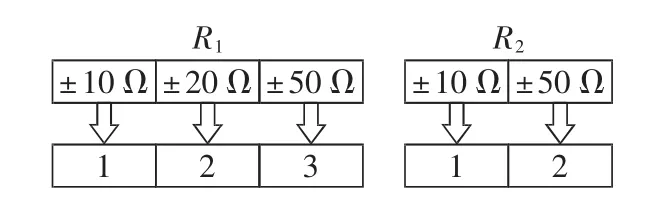
图2 容差整数化示例Fig.2 Example of tolerance integralization

3 智能电能表容差设计实例

本文以单相智能电能表的计量电路为研究对象，进行各元器件的容差优化设计，其流程如图3所示。在确定各元器件参数的容差等级并整数化后，采用蒙特卡洛法在参数的变化范围内生成若干样本点，并通过仿真得到样本点处的目标函数值和约束函数值。在此基础上，基于神经网络建立目标函数和约束条件的近似模型，并运行分支定界算法进行容差设计优化。在反复评估目标函数值和约束条件后，若无法得到最优解则插入更多样本点对模型加以精化，继续执行优化程序直到获得最优解。单相智能电能表计量电路的电压、电流通道电路图如图4所示。本文选取电压量限为220 V、负载电流为In、功率因数为1的情况，进行电能表的基本误差计算。

在保证批次智能电能表的误差范围不超过自定义界限EC的同时，产品具有最低成本，其容差设计模型可表示为：

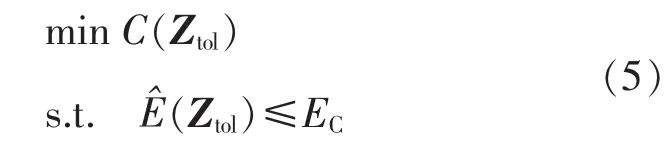
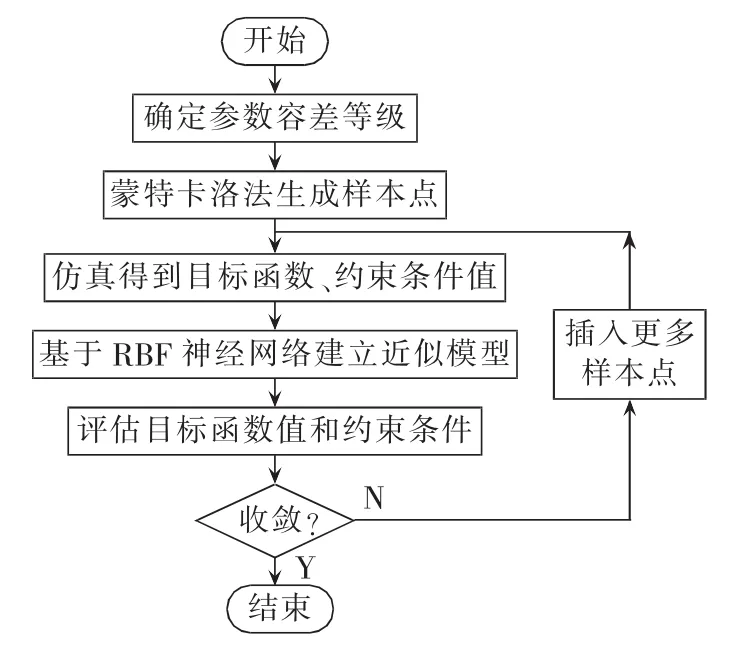
图3 计量电路容差设计流程图Fig.3 Flowchart of tolerance design of metering circuit

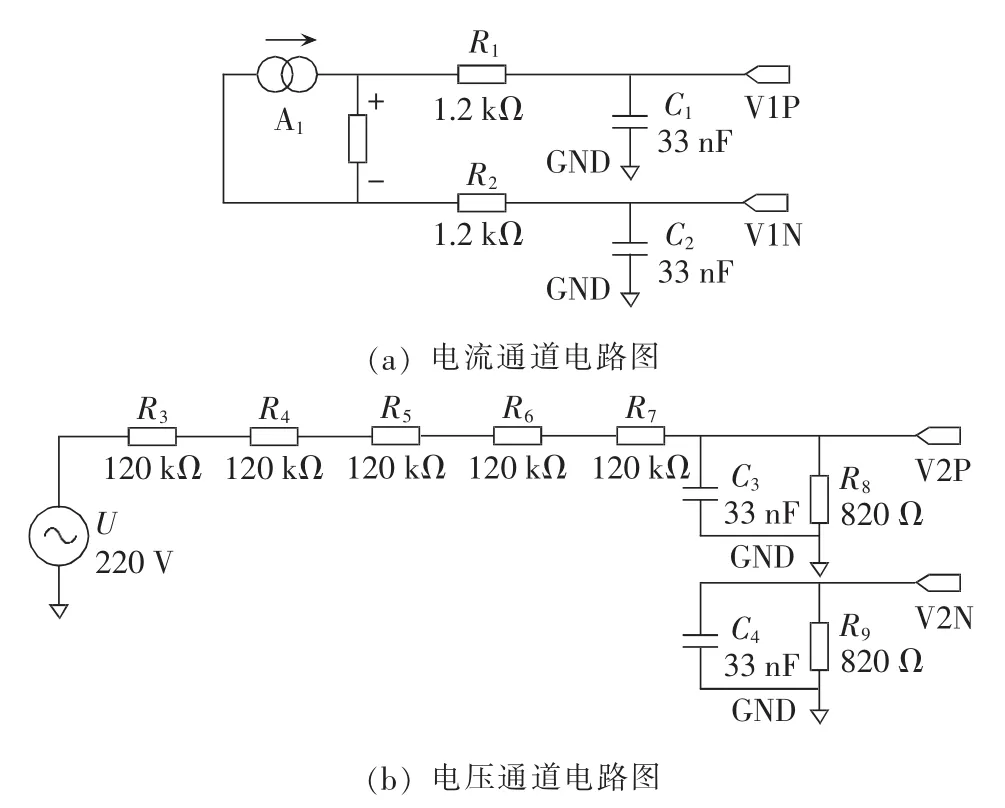
图4 计量电路原理图Fig.4 Schematic diagrams of metering circuit

其中，C（Ztol）是成本模型；（Ztol）是通过 RBF 神经网络模型近似后的基本误差范围模型。

计量电路中各元器件的精度等级转化为整数形式，如表2所示。采用试验设计方法，列举各种精度等级的组合情况，并对每一种情况下电压、电流通道的误差进行蒙特卡洛分析。针对一种精度等级组合，在各个元器件对应的容差范围内，通过随机生成15 000组描述电子元件参数数值的样本点进行蒙特卡洛分析。该15000个样本的生成根据6σ准则，且满足正态分布。在Simulink平台上建立计量电路的仿真模型，得到各容差组合下的计量误差分布。

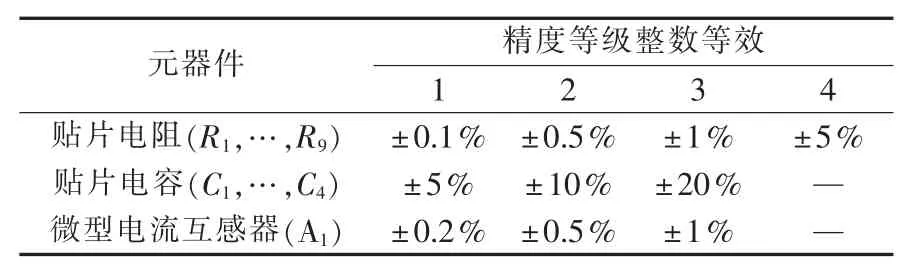
表2 各元器件精度等级Table 2 Accuracy grades for different components

反向传播（BP）神经网络是指基于误差反向传播算法的多层前向神经网络，具有较好的近似精度和实用性［18-19］。典型的BP神经网络由输入层、隐含层和输出层构成。将神经网络应用于产品容差设计时，输入层接收各设计参数的容差等级值进行内部学习和处理；输出层输出计量相对误差的具体值。本文应用神经网络建立基本误差的数值模型，选择收敛速度较快的L-M（Levenberg-Marquardt）算法，依据经验和实验的方法，选取隐含层神经元个数为8个，可获得较好的结果。根据90个数据样本，选取72个样本作为训练样本，另外18个样本作为检验模型的仿真预测结果，学习过程如图5所示。在训练68步后，满足所定义的拟合精度指标要求（误差为3%）。

图5 L-M优化学习算法的迭代效果Fig.5 Iteration effect of L-M optimization algorithm

各元器件不同精度等级时的成本如表3所示，分别选用倒数模型、线性模型和多项式模型对贴片电阻、贴片电容和微型电流互感器的“成本-公差”模型进行拟合，得到容差设计的目标函数为：

其中，ztolR、ztolC和ztolA分别是单只贴片电阻、贴片电容和微型电流互感器的等效容差值，有 ztolR∈｛1，2，3，4｝、ztolC∈｛1，2，3｝和 ztolA∈｛1，2，3｝。

表3 元器件成本模型Table 3 Cost model for different components

本文选取4个误差范围界限，根据式（5）和式（6）对电能表计量采样电路进行容差设计，优化结果如表4所示。当误差范围允许界限EC设置为相对较大值2.5%时，产品最低成本为3.38元，各元器件的容差等级取值较大；当EC逐渐减小，产品成本随之提高，某些元器件容差等级取值减小。在同样的误差范围界限设置下，采用传统面向连续设计变量的容差设计方法进行优化设计，元器件精度结果如表5所示，其中加粗数值的元器件精度在实际工程应用中无法提供。

表4 容差设计优化结果Table 4 Optimization results of tolerance design

对比表4和表5可知，在同一误差允许范围界限EC下，传统方法所给出的产品成本更低，但由于工程上无法满足部分元器件的精度要求，所以此时的产品成本并不是真实成本，而是需要进一步列举精度等级组合，直到获得最优组合为止。以EC取值2.5%为例，存在 R3、R4、R5、R6、R7、R86 个贴片电阻的精度未知，每一个电阻选取位于优化值附近的精度值，即R3、R4、R5、R6、R7选择 ± 1% 和 ± 5%，R8选择 ± 0.1%和±0.5%，则需要对26组精度组合进行比较，采用枚举法选取成本最小的组合。

由以上分析可知，传统容差设计方法无法直接获得最终优化值，需要再次通过枚举法进行选取，计算成本较高；而本文提出的方法在计算成本上更具优势，适用于离散设计变量的优化设计。

针对应用本文方法的4种优化方案，在对应的容差等级下分别选取2500个样本进行仿真计算，得到的误差分布直方图如图6所示。从图中可以看出：随着误差范围允许界限EC越来越小，电路成本增加，基本误差分布范围变小，即误差一致性提高。因此，设计人员可以通过设定目标误差范围，获得在此误差范围界定下使得成本最小的容差方案，以权衡成本和误差一致性。

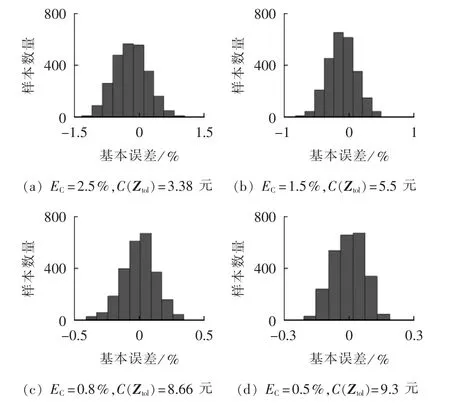
图6 基本误差分布直方图Fig.6 Histogram of basic error distribution

表5 传统方法优化结果Table 5 Optimization results of traditional method

4 结论

本文从“成本-公差”模型的角度出发，分析并建立了单相智能电能表的容差设计模型，提出了以生产成本最小作为优化目标、以计量基本误差范围为约束条件的优化方程。此外，针对包含离散设计变量的优化问题，提出了一种以整数线性规划思想为基础、基于分支定界算法的容差设计方法。最后，采用该算法对典型的单相智能电能表计量电路进行了容差设计，得到了在不同误差变化范围界限值下的各元器件公差值，验证了该算法的有效性。设计人员可以权衡待生产电能表的目标误差范围，灵活选取各元器件的精度等级，在保证批次计量误差一致性的同时，节约加工成本。

［1］沈明炎.单相智能电能表实际负载下的误差试验与分析［J］.工业计量，2014，24（2）：14-18.SHEN Mingyan.The error test and analysis of single-phase intelligent electricity meter with actual load［J］.Industrial Measurement，2014，24（2）：14-18.

［2］袁金灿，马进，王思彤，等.智能电能表可靠性预计技术［J］.电力自动化设备，2013，33（7）：161-166.YUAN Jincan，MA Jin，WANG Sitong，et al. Reliability prediction of smart electrical energy meter［J］.Electric Power Automation Equipment，2013，33（7）：161-166.

［3］黄艳，周文斌，吴晓昱，等.智能电能表的发展应用及误差调整［J］. 电测与仪表，2012，49（10A）：36-39.HUANG Yan，ZHOU Wenbin，WU Xiaoyu，etal.Development and the way of error adjustment of smart electricity meter［J］.Electrical Measurement&Instrumentation，2012，49（10A）：36-39.

［4］蓝永林.交流电能计量［M］.北京：中国质检出版社，2011：277.

［5］中华人民共和国国家质量监督检验检疫总局.多费率电能表特殊要求：GB/T115284—2002［S］. 北京：中国标准出版社，2002.

［6］李建华.智能电能表误差与一致性误差问题分析［J］.江苏现代计量，2014（8）：24-28.LI Jianhua.Error and consistent error analysis of intelligent electricity meter［J］.Jiangsu Present Day Metrology，2014 （8）：24-28.

［7］周文斌，黄艳.智能电能表的误差调整方式［J］.中国计量，2012（11）：69-70.ZHOU Wenbin，HUANG Yan.The way of error adjustment of smart electricity meter［J］.China Metrology，2012（11）：69-70.

［8］MCNEILL N，DYMOND H，MELLOR P H.High-fidelity low-cost electronic current sensor for utility power metering ［J］.IEEE Transactions on Power Delivery，2011，26（4）：2309-2317.

［9］PEREIRA P，FINO M H，COITO F V.Using discrete-variable optimization for COMOS spiral inductor design［C］∥International conference on microelectronics. Marrakech，The Kingdom of Morocco：［s.n.］，2009：324-327.

［10］ZHANG J，CHUNG H S，LO A W，et al.Extended ant colony optimization algorithm for power electronic circuit design ［J］.IEEE Transactions on Power Electronics，2009，24（1）：147-162.

［11］肖华辉.智能电能表误差分析及控制措施［J］.科技与创新，2015（1）：143-144.XIAO Huahui.Smart meter error analysis and control measures［J］.Science and Technology&Innovation，2015（1）：143-144.

［12］王学伟，温丽丽，贾晓璐，等.智能电能表动态误差的OOK激励测试方法［J］. 电力自动化设备，2014，34（9）：143-147.WANG Xuewei，WEN Lili，JIA Xiaolu，et al. OOK-driven dynamic error measurement of smart energy meter［J］.Electric Power Automation Equipment，2014，34（9）：143-147.

［13］朱学贵，覃阳，苏向丰，等.电动汽车充电机对电能计量的影响［J］. 电力自动化设备，2015，35（6）：52-57.ZHU Xuegui，QIN Yang，SU Xiangfeng，et al.Impact of electric vehicle charger on electric energy metering［J］.Electric Power Automation Equipment，2015，35（6）：52-57.

［14］李泽文，舒磊，邓丰，等.基于全数字锁相环的电力系统高精度同步时钟［J］. 电力自动化设备，2015，35（7）：32-36.LIZewen，SHU Lei，DENG Feng，etal.WhollyDPLL-based synchronous clock with high precision for electric power system［J］.Electric Power Automation Equipment，2015，35（7）：32-36.

［15］CHASE K W，GREENWOOD W H，LOOSLI B G，et al.Least cost tolerance allocation for mechanical assemblies with automated process selection ［J］.ASME Manufacturing Review，1990，3（1）：49-59.

［16］杨金涛，乐健，刘开培，等.基于LCC的配电网供电电压质量改善措施的优化［J］. 电力自动化设备，2015，35（8）：59-64.YANG Jintao，LE Jian，LIU Kaipei，et al.Improvement measure optimization based on LCC for voltage quality of distribution network［J］.Electric Power Automation Equipment，2015，35（8）：59-64.

［17］MEYER X，CHOPARD B，ALBUQUERQUE P.A branch-andbound algorithm using multiple GPU-based LP solvers［C］∥International Conference on High Performance Computing.Bangalore，India：［s.n.］，2013：129-138.

［18］戴志辉，李芷筠，焦彦军，等.基于BP神经网络的小样本失效数据下继电保护可靠性评估［J］. 电力自动化设备，2014，34（11）：129-134.DAI Zhihui，LI Zhijun，JIAO Yanjun，et al. Reliability assessment based on BP neural network for relay protection system with a few failure data samples［J］.Electric Power Automation Equipment，2014，34（11）：129-134.

［19］吴启蒙，魏明，樊高辉，等.基于BP神经网络的静电放电电流解析表达式［J］. 高电压技术，2012，38（11）：2912-2918.WU Qimeng，WEI Ming，FAN Gaohui，et al.Analytical expressions ofelectrostatic discharge currentbased on the BP neural network［J］.High Voltage Engineering，2012，38（11）：2912-2918.