TS-PID算法的直流伺服控制系统*

高　嵩，王　磊，陈超波，张彬彬（西安工业大学电子信息工程学院，西安710021）



TS-PID算法的直流伺服控制系统*

高嵩，王磊，陈超波，张彬彬
（西安工业大学电子信息工程学院，西安710021）

摘 要：针对传统的PID无法使得直流电机达到精确的控制效果，本文将TS模糊控制方法与PID控制器相结合并将其应用于直流电机的位置伺服控制系统当中．建立了直流电机的模型，根据TS模糊控制规则，在Matlab仿真环境中建立了基于TS-PID算法的直流电机的仿真模型，将控制系统的参数带入仿真模型中并进行实验仿真．通过与传统PID控制算法相比较．仿真实验结果表明：TS-PID控制的直流伺服控制系统在单位阶跃输入下上升时间降低了17．23%，调节时间缩短了29．32%，稳态误差减少了0．12%．系统具有较好的动态性能、较强的抗干扰能力和较快的跟踪速度．

关键词：TS-PID控制；伺服控制；直流电机；时域性能

基金资助：兵器预研支撑基金（62201070317）；陕西省国际科技合作重点项目（2015KW-024）

伺服控制系统是利用反馈原理通过各种控制方法和策略，使得输出量服从输入的运动控制系统．直流电机具有优良的性能，在电机控制领域获得了广泛的应用［1-6］．但是无刷直流电机存在参数时变和被控对象的非线性问题，传统PID控制器较难达到精确地控制．近年来，越来越多的研究关注于直流伺服控制系统的研究．如文献［7］采用基于改进遗传算法优化模糊PID的控制方法，不仅缩短了无刷直流电机的阶跃响应时间和延迟时间，而且降低了控制的误差，但是算法中的编码和解码过程较为繁琐．文献［8］提出了一种基于粒子群优化的PID控制器，使得优化后的控制器速度响应快，超调量小，系统具有较好的动静态性能，但是评价指标的选取较为困难．文献［9］采用神经网络自适应滑模变结构控制来提高无刷直流电机调速驱动系统的性能，控制系统具有较好的时域性能和鲁棒性，但是其运算量较大．文献［10］提出了基于自抗扰控制器的永磁无刷直流电机转矩波动抑制控制方法，使得电机具有良好的动静态性能、较好的适应性和鲁棒性，然而其设计较为复杂．

根据直流伺服控制系统的时域性能分析，采用TS-PID模糊控制器来控制直流电机．模糊控制器具有能适应被控对象非线性和时变性的特点，而且鲁棒性较好．但是其稳定精度较差，难以达到精确的控制，对此将位置环控制器采用模糊控制和PID控制相结合的方法来对其进行改进．模糊PID既具有模糊控制的优点，同时具有PID控制的能抑制稳态误差的特点，可实现对PID参数的在线调整．采用TS-PID控制算法，通过模糊控制的机理，根据控制系统实际输入输出响应来设置模糊规则，实现对TS-PID参数的最佳调整．

1　直流伺服控制系统

模糊控制和PID控制相结合的方法，相对比传统的PID控制算法，可以提高系统的时域性能以及抗干扰性［11］．TS模糊控制是采用分段线性控制实现全局的非线性控制算法，PID控制是将控制系统偏差的比例、积分和微分通过线性组合，实现对控制对象的控制．将TS控制与PID控制相结合构成TS-PID控制器并运用于直流伺服控制系统，根据系统的特征设计模糊规则，通过阶跃响应和正弦响应来验证算法对系统的作用．

1．1 伺服控制系统整体结构

伺服控制要求系统能够稳定快速的跟踪给定信号，与传统的位置速度环或位置加速度环相比，本文采用位置、速度和电流三闭环控制策略．电流环主要是构成电流负反馈，抑制电流的波动．速度环使得转速能够跟随给定电压的变化，对负载的变化起到抗扰作用．位置环实现对给定位置的准确与快速跟踪．

1．2 直流电机的数学模型

直流伺服控制系统的直流电机等效电路图如图1所示．图中Ud为功率驱动的输出平均电压，Id为电机回路的平均电流，电阻R为整个回路的等效电阻，L为整个回路的等效电感，E为电机的反电动势，n为电动机的转轴转速，Te为电动机的电磁转矩，TL为电动机的负载转矩．

图1　直流电机的等效电路图Fig．1 Equivalent-circuit of DC motor

直流电机的等效回路电压方程为

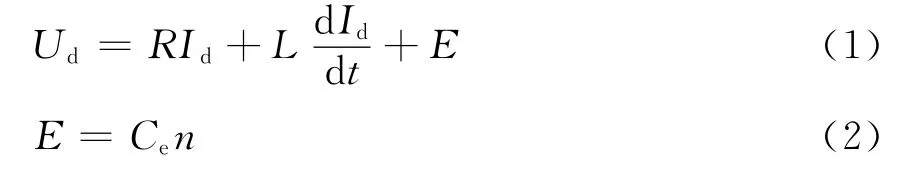
其中Ce为直流电动机的反电动势系数．电动机转轴的动力学方程为

式中：GD2为电动机的飞轮惯量．引入两个参数，电枢回路的电磁时间常数Tl和电机拖动系统中的机电时间常数Tm，其中

由此可得电压与电流的关系式为

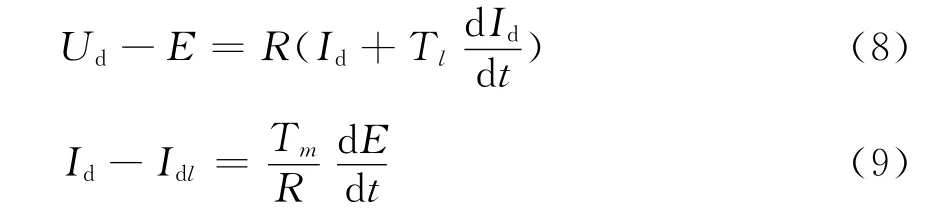
由式（8）～（9）可以分别得直流电动机内部的整体系统结构框图如图2所示．

图2　电动机内部的整体结构框图Fig．2 Internal structure of the DC motor

1．3 功率驱动模块

电机要求能实现正反转运行，所以直流电机驱动模块选择桥式功率放大电路．功率驱动模块结构图如图3所示．控制器的电源电压为Us，通过PWM变换器，输出的平均电压为Ug，通过功率放大后，得到直流电机的控制电压Ud．

PWM模块的平均输出电压Ug和占空比ρ满足数学关系为

整个功率驱动模块可以看成是一个纯滞后模型，其传递函数为

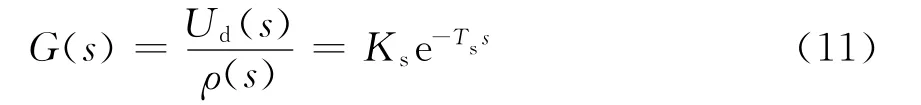
式中：Ks为变换器放大系数；Ts为变换器滞后时间常数．通常将PWM的传递函数当成一阶惯性环节，其近似传递函数为

图3　功率驱动模块示意图Fig．3 Structure of power driving module

1．4 转速和电流双闭环直流调速系统

直流伺服控制系统要求能够尽可能的减少启动和制动时间，其启动和制动过程为准时间最优控制．转速、电流双闭环直流调速系统的结构图如图4所示．

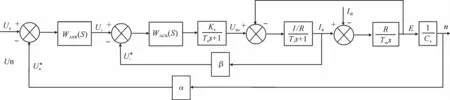
图4　转速和电流直流调速系统结构示意图Fig．4 Structure of DC speed control system for the speed and current

图4中电流控制器与速度控制器分别采用PI控制．其中电流环控制器和速度环控制器分别为

式中：KI与τI分别为电流环的比例参数和积分参数；KN与τN分别为速度换的比例参数为积分系数．

2　TS模糊控制算法

2．1 TS模糊模型的基本原理

Zadeh分别于1965年和1973提出了模糊集理论和模糊推理理论［11-13］．模糊控制是以模糊集合论和模糊逻辑推力为理论基础，以传感器技术和计算机技术为基础的控制方法．模糊控制方法通常应用于被控对象的模型没有精确的数学表达式，模糊控制需要通过专家的经验来建立适当的模糊控制规则．TS模糊控制器适用于局部非线性精确逼近，可以根据直流伺服控制系统进行分段控制，对于各个分段设计局部的控制规则，最后组成全局TS模糊控制．

2．2 TS模糊控制规则

TS模糊控制器输出的是数值函数，可以便于对整个系统进行精确控制．假设TS模糊模型的输入变量为x＝［x1，x2，…，xn］T，每个分量xj的模糊集为

做好绿色植保建设。以项目实施规模为以及，进行了5盏太阳能杀虫灯配备，安装了2800黄板，蓝板600张，食诱箱30个。

2．3 输入变量的模糊等级划分和隶属度函数

输入变量选择偏差e和偏差的变化率Δe，将偏差e划分为五个模糊等级，分别为NB、NS、ZO、PS 和PB．而偏差的变化率Δe划分为三个模糊等级，分别为N，Z和P．其模糊隶属度函数选择三角函数，其隶属度函数如图5和图6所示．偏差e和偏差的变化率Δe通过尺度变换求出其模糊集合．

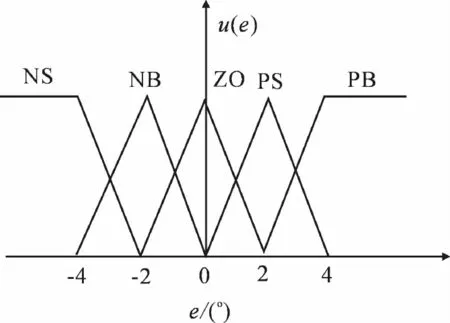
图5　偏差e的隶属度函数Fig．5 Membership function of bias of e

图6　偏差变化率Δe的隶属度函数Fig．6 Membership function of change rate bias ofΔe

2．4 TS型模糊推理

模糊推理是模糊控制的关键部分，它根据输入变量和模糊规则，通过逻辑运算得到系统的输出．计算控制器的输出时，采用线性加权求和方法，即

式中：m为某一种输入下激活的模糊规则数目；ω为每条规则的权重系数，文中采用的算法中规则的权重采用取小法．

3　TS-PID控制器的设计

TS-PID控制器是采用局部线性来实现全局的非线性控制．通过对控制过程进行分析，设计出合理的规则，将调节的经验设定为控制规则实现非线性控制，TS-PID控制器的控制原理图如图7所示．

通过经验总结可知，偏差e和偏差的变化率Δe 与PID控制器的三个参数Kp、Ki和Kd之间存在以下关系．当|e（t）|较大时，应取较大的比例系数Kp和较小的Kd，使控制系统具有较好的跟踪性能，同时对Ki进行限制，避免出现较大的超调．当|e（t）|处于中等时，应取较小的Kp和Ki，使得系统响应的超调量较小，Kd的取值要恰当，Ki不能过大．当|e（t）|较小时，主要是消除稳态误差，此时应增大Kp和Ki，减小Kd，并且避免出现振荡．

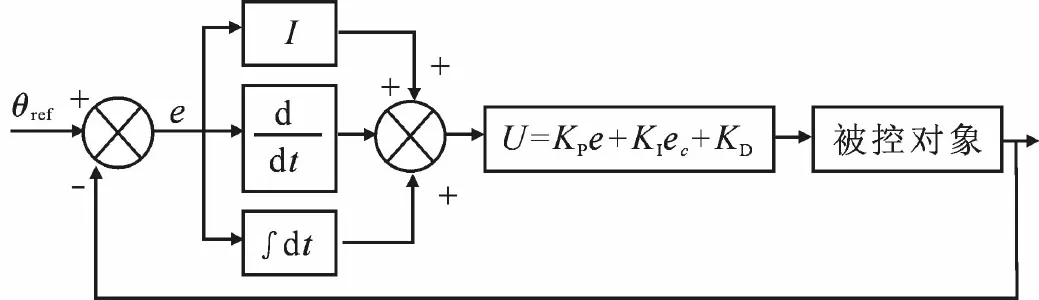
图7　TS-PID控制器结构图Fig．7 Structure of TS-PID controller

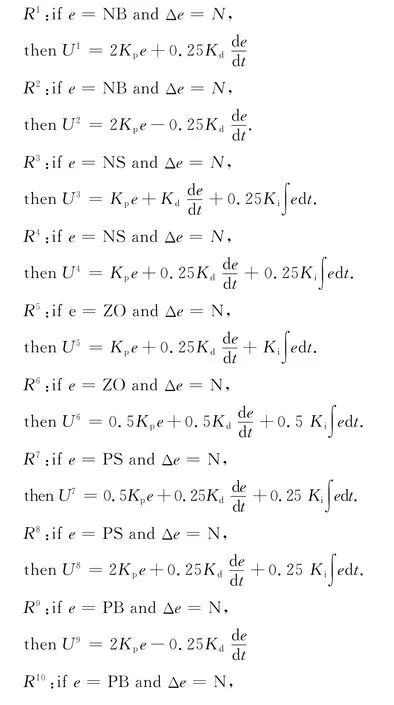
TS模糊推理的输出直接为数字量，通过模糊推理对分段线性输出的结果采用加权平均法得到控制器的输出量．

4　实验仿真分析

根据本文所采用的方法，在matlab仿真环境中搭建实验仿真模型．图8为模糊PID伺服控制系统的Simulink仿真模型．

图8　模糊PID控制系统的仿真模型Fig．8 Simulation model of fuzzy PID control system

文中采用直流电机调速系统电机参数见表1．

表1　直流电机调速系统的参数Tab．1 Parameters of DC motor speed control system

采用传统的PID参数整定方法得到的参数值为Kp＝5．5，Ki＝0．05，Kd＝0．01．当输入为单位阶跃函数时，在t＝2 s时，输入扰动d（t）＝－0．2（t－2），传统PID控制与TS-PID控制的阶跃响应如图9所示．

由图8可知，TS-PID控制算法使得控制系统具有较小的上升时间，并且在受到外界扰动时，能够快速的恢复到稳定状态，系统具有较强的抗干扰性能．

表2所示为传统PID控制器与TS-PID控制器下的系统性能指标．

图9　传统PID与TS-PID的单位阶跃响应曲线对比Fig．9 Comparison between unit-step responses of the traditional PID and TS-PID

表2　不同控制器下系统性能指标对比Tab．2 Comparison of Performance indicators with different control systems

由表2可知，采用TS-PID控制方法，系统的上升时间减少了17．23%，调节时间缩短了29．32%，稳态误差降低了0．12%，系统的性能指标较传统PID控制系统有较大提高．

当控制系统的输入为正弦波时，TS-PID控制与传统PID控制的系统输出响应曲线如图9所示．

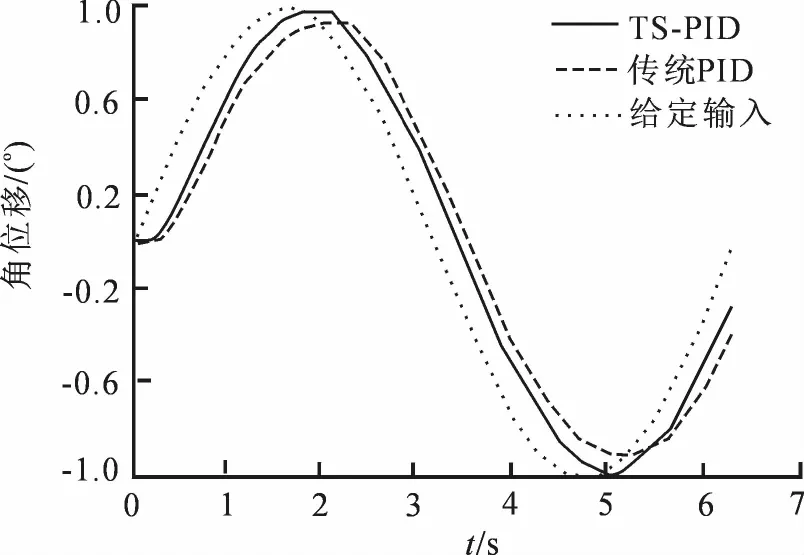
图10　传统PID与TS-PID的正弦响应对比Fig．10 Comparison between sine response of the traditional PID and TS-PID

由图10可知，当输入为正弦波时，TS-PID控制器的滞后时间比传统控制器较小，具有较快的跟踪速度．由此可知，TS-PID控制器的反应速度也较传统PID控制系统的反应速度更快．

5　结论

针对直流电机伺服控制系统的高阶次与非线性特性的特点，采用了基于TS-PID的控制算法．首先建立了直流电机的模型，然后根据TS模糊控制规则设计了TS-PID控制器，最后将其应用于直流电机位置伺服控制系统上．通过与传统PID控制算法相比较，仿真实验结果表明本文所提方法具有较好的动态性能，系统的抗干扰能力较强．

参考文献：

［1］ 夏长亮，方红伟．永磁无刷直流电机及其控制［J］．电工技术学报，2012，27（3）：25．XIA Changliang，EANG Hongwei．Permanent-Magnet Brushless DC Motor and Its Control［J］．Transactions of China Electrohnical Society，2012，27（3）：25．（in Chinese）

［2］ 纪梁洲，杨向宇，龚晟．多功能无刷直流电机驱动控制器的研制［J］．微电机，2011，44（4）：64．JI Liangzhou，YANG Xiangyu，GONG Sheng．Research on Multiple Eunctions of Brushless DC Motor Drive［J］．Micronotors，2011，44（4）：64．（in Chinese）

［3］ 余安富，于平，李先锋，赵昶宇．基于TMS320E28335的无刷直流电机调速系统设计［J］．仪表技术与传感器，2011（9）：102．YU An-fu，YU Ping，LI Xianfeng，ZHAO Changyu．Brushless DC Motor Speed Control System Design Based on TMS320E28335［J］．Instrument Technique and Sensor，2011（9）：102．（in Chinese）

［4］ 陆地，李甲锋，王建信．一种高可靠性直流无刷电机调速装置［J］．哈尔滨理工大学学报，2011，16（6）：46．LU Di，LI Jiafeng，WANG Jianxin．A Highly Reliable Brushless DC Motor Speed Control Device［J］．Journal of Harbin Unviersity of Science and Technology，2011，16（6）：46．（in Chinese）

［5］ 肖金凤，张垒，盛义发．无刷直流电机磁场定向控制策略研究与实现［J］．控制工程，2013，20（1）：158．XIAO Jinfeng，ZHANG Lei，SHENG Yifa．Research on and Implementation of Eield Orientation Control Strategy of Brushless DC Motor［J］．Control Engineering of China，2013，20（1）：158．（in Chinese）

［6］ 夏鲲，朱琳玲，曾彦能，徐鑫悦，杨益华．基于准Z源网络的永磁无刷直流电机换相转矩脉动抑制方法［J］．中国电机工程学报，2015，35（4）：971．XIA Kun，ZHU Linling，ZENG Yanneng，XU Xinyue，YANG Yihua．Research on the Method of Suppressing Commutation Torque Ripple for Brushless DC Motors Based on a Quasi-Z-Source Net［J］．Proceedings of the CSEE，2015，35（4）：971．（in Chinese）

［7］ 张淑梅．改进遗传优化的无刷直流电机模糊PID控制［J］．计算机仿真，2014，31（10）：410．ZHANG Shumei．Euzzy PID Control of Brushless DC Motor Based on Improved Genetic Algorithm［J］．Computer Simulation，2014，31（10）：410．（in Chinese）

［8］ 任志斌，王业占，梁建伟．基于粒子群优化设计的直流无刷电机控制系统研制［J］．微电机，2011，44（8）：64．REN Zhibin，WANG Yezhan，LIAN Jianwei．Controlling of Brushless DC Motor Based on Particle Swarm Optimization Controller［J］．Micromotors，2011，44 （8）：64．（in Chinese）

［9］ 李军红，李兰君，阳武娇．无刷直流电机调速系统神经网络自适应滑模变结构控制［J］．微计算机信息，2010，26（4）：68．LI Junhong，LI Lanjun，YANG Wujiao．Neural Adaptive Sliding Model Variable Structure Control for Brushless DC motor Speed Systems［J］．Control＆Automation，2010，26（4）：68．（in Chinese）

［10］ 夏长亮，俞卫，李志强．永磁无刷直流电机转矩波动的自抗扰控制［J］．中国电机工程学报，2006，26 （24）：137．XIA Changliang，YU Wei，LI Zhiqiang．Torque Rip-ple Reduction of PM Brushless DC Motors Based on Auto-disturbances-rejection Controller［J］．Proceedings of the CSEE，2006，26（24）：137．（in Chinese）

［11］ 高嵩，朱峰，肖秦琨，何宁．机载光电跟踪系统的模糊自整定PID控制［J］．西安工业大学学报，2007，27 （4）：312．GAO Song，ZHU Eeng，XIAO Qinkun，HE Ning．Research on Euzzy Self-adjusting PID Control of Airborne Electro-optical Pointing and Tracking Systems［J］．Jouranal of Xi’an Technological Univerity，2007，27（4）：312．（in Chinese）

［12］ ZADEH L A．Euzzy Sets［J］．Information and Control，1965，8（3）：338．

［13］ ZADEH L A．Outline of a New Approach to the A-nalysis of Complex Systems and Decision Processes ［J］．IEEE Transactions on Systems，Man and Cybernetics，1973，3（1）：28．

（责任编辑、校对 张立新）

DC Servo Control System Based on TS-PID Algorithm

GAO Song，WANG Lei，CHEN Chaobo，ZHANG Binbin
（School of Electronic Information Engineering，Xi’an Technological University，Xi’an 710021，China）

Abstract：The traditoinal PID control algorithm can not control DC motors accurately．In order to improve the control effect，the TS-PID algorithm is applied in the DC servo control system．The model of DC motor is built．According to the mechanisms of TS fuzzy control system，the simulation model of DC servo control system is established in the Matlab simulation based on TS-PID control algorithm．The comparison of the new algorithm with the traditional PID control algorithm shows that，with unit step input，the rising time reduces by 17．23%，the regulation time decreases by 29．23%and steady state error decreases by 0．12%．The system has better dynamic performance，faster tracking velocity and the stronger capability of anti-jamming．

Key words：TS-PID control；servo control；DC motor；time domain performance

作者简介：高 嵩（1966－），男，西安工业大学教授，主要研究方向为智能控制、多传感器信息融合、计算机控制、自主智能体及复杂网络控制等．E-mail：602507619＠qq．com．

*收稿日期：2014-11-13

DOI：10．16185／j．jxatu．edu．cn．2016．01．004

文献标志码：中图号： TP273＋．4 A

文章编号：1673-9965（2016）01-0014-07