双环重复控制三相四线制有源电力滤波器
黄海宏 ,王 钰,许若冰 ,杨佳能
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009;2.国网南京供电公司,江苏 南京 210019)
0 引言
随着现代工业的发展,非线性负载开始广泛使用,谐波及无功电流对电网的污染已不容忽视,有源电力滤波器APF(Active Power Filter)的诞生为此提供了有效的解决方案。目前三相三线制APF应用已较为成熟,而对于我国大多采用三相四线制线路的市政电网,三相四线制并联APF[1-2]由于能够补偿网侧三相和中线上谐波及无功电流,开始逐步受到关注。
目前,APF电网电流检测算法主要有如下4种。①基于瞬时无功功率理论的实时检测法[3],其主要包含p-q法和ip-iq法。这2种方法补偿效果都比较明显,但由于其原理是建立在对称的三相三线制电路基础上,三相电流不含零序分量,故而在应用广泛的三相四线制线路中并不适用。②基于傅里叶级数的变换法[4]。该方法具有较高的检测精度而且可以对基波和指定谐波进行检测,但由于对周期数据的分析,不适宜快速实时控制。③基于dq0坐标变换的广义瞬时无功功率法[5]。由于该方法可对零序电流进行运算变换,故而适用于三相四线系统。假设应用该方法进行同步坐标变换并断开瞬时无功q轴滤波通道得到指令电流,其补偿后三相网侧电流只含对称的基波正序有功分量且中线电流为0,这将导致APF向网侧注入大量基波电流不对称分量,严重增加了开关器件流通电流大小。④基于瞬时无功功率理论改进的单相谐波检测方法[6],该方法在单相APF中有过应用。本文考虑到三相四线制系统可以看作3个依次滞后120°的单相系统组合,故而可分别通过低通滤波器获得每相的基波有功电流,使得APF仅需补偿无功及谐波电流,并使中线补偿后只含基波电流。 而 FBD(Fryze Buchholz Dpenbrock)[7]、自适应、神经网络检测、小波检测等其他检测手段也曾是 APF 研究的热点[8-10]。
在控制算法层面,基于PI调节的三角载波比较控制法在传统的APF控制中被广泛应用,但由于PI控制只可以无静差地跟踪直流信号,该电流控制模式在实际的APF应用中并不能获得较满意的稳态特性。基于内模原理的重复控制理论上能够在谐波频率处获得无穷大增益[11],提高稳态特性,但是动态性能较差。为此本文总结其他改进方法[12-15]并简化得出了一种双环重复控制系统,将比例控制的快速性引入,使得整个APF系统能够获得快速高稳态的补偿性能。
在此基础上,在实验室搭载了一台380 V三相四线制APF,并采用TI公司的TMS320F2812DSP芯片作为主控系统,通过仿真和实验验证了本文提出方法的补偿效果。
1 谐波检测算法选择
对于三相四线制APF,目前应用较多的是基于dq0坐标变换的检测方法,即引言提及的方法③,其检测原理框图如图1所示。

图1 基于dq0坐标变换的检测原理框图Fig.1 Schematic diagram of detection based on dq0 coordinates transformation
通过图1可以看出,基于dq0坐标变换的检测方法是通过同步坐标变换,将abc坐标系下的三相负载电流变换到dq0同步旋转坐标系中,原三相基波正序电流分量转成dq0坐标系中直流分量,其余分量则转成dq0坐标系中交流分量。在这里设计APF可补偿谐波及基波正序无功电流,因此断开q轴通道,即只用低通滤波器(LPF)滤得d轴直流分量,再经同步坐标反变换得到的便是与三相系统基波正序电压同频同相的基波正序有功电流,从而可方便地得出需补偿的指令电流。
基于dq0坐标变换的检测方法能准确检测出三相四线系统中需补偿的指令电流(含基波正序无功电流、基波电流不对称分量及谐波电流)。其网侧补偿后理想效果为对称的基波正序有功电流,因此APF除需补偿基波正序无功及谐波电流外,还需补偿大量基波电流不对称分量。基波电流不对称分量在APF系统的能量流动中表现为瞬时无功功率,虽然对直流侧和交流侧进行的能量交换没有作用,但是在三相间的功率交换会严重增加开关管流通电流大小,在设计时也必须考虑到开关器件容量的增加。
由以上分析可以看出,APF应用dq0坐标变换检测法时的开关器件容量选取值要比仅补偿基波正序无功及谐波电流时增大不少。事实上,三相四线不平衡系统中的中线基波电流是由负载基波电流不对称分量中的零序分量导致的,原则上属于配电问题,不在APF的补偿范围内,一般对入网中线电流的要求是不超过其额定值的25%即可。故而在实际应用中从降低开关器件成本角度考虑,APF无需对基波电流不对称分量全部补偿,而对于基波电流不对称分量中的基波无功电流部分可给予补偿。
为了寻找解决以上问题的最佳方案,使得APF仅补偿无功及谐波电流并降低开关器件容量选取值,本文将基于单相谐波检测的新方法应用于三相四线制系统中,即引言部分提到的方法④推广。该方法的实质是将待测的三相瞬时电流与和电网电压同频同相的正弦信号相乘,并分别通过低通滤波器,再经运算得出每相的基波有功电流,最后通过负载电流与基波有功电流相减得到仅需补偿的无功及谐波电流。该方法的具体流程见图2,由逆变器向电网注入与检测出的无功及谐波电流相反的补偿电流,便可极大程度地改善网侧畸变电流波形,提高电能质量。
2 双环重复控制策略分析
重复控制器是基于内模原理提出的控制方案。若APF需补偿的谐波信号具有周期性,则在控制器中嵌入一个基波周期的延时,对误差信号进行周期性累加,便可减少系统的静态误差。由于重复控制器可在谐波频率处提供无穷大增益,能使电流控制环的稳态精度得到提高。但是传统的重复控制策略在补偿时存在一个周期的延迟,在动态性能上表现不佳。为此,本文总结其他改进方法并简化得出了一种双环重复控制策略,其结构框图如图3所示。
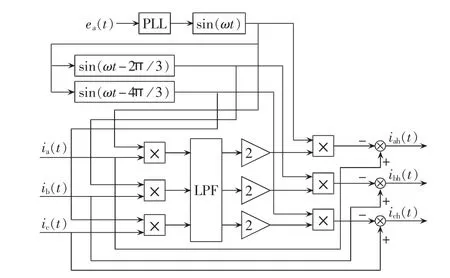
图2 谐波检测方法原理图Fig.2 Schematic diagram of harmonic detection

图3 双环重复控制策略结构图Fig.3 Structural diagram of dual-loop repetitive control
双环重复控制系统结构的设计主要分为重复控制器和电流内环两部分。谐波电流指令i*ref除输入给重复控制器外,还前馈至电流内环对Gp(z)进行比例控制。重复控制器保证了系统的稳定性,使系统做到无静差跟踪谐波指令;而电流内环的比例控制保证了系统的动态快速性,使系统可对谐波指令的变化产生快速响应。
2.1 电流内环设计
首先分析电流内环的受控对象离散模型Gp(z),采用单电感进行网侧滤波,被控对象的s域模型为:

取电感L=2 mH,电感等效电阻R1=0.05 Ω。实验中开关频率为9 kHz,采用双倍开关频率18 kHz来进行采样,则Gp(s)经过零阶保持器离散化得:

由于电流内环的闭环特性由其开环传递函数决定,故在电流内环前向通道中加入比例控制Kp以提高开环高增益并拓展带宽,其值由经验公式推导:

其中,Ts为载波周期;fPWM为开关频率。电流内环的闭环传递函数为Gc(z),且不考虑扰动分量,则:

其伯德图见图4。由图可知,电流内环在中低频段幅值接近于1,而在中高频段幅值衰减缓慢,且相位滞后严重,将引入系统高频分量并导致整个系统的不稳定,故而需要通过重复控制器外环进行校正。

图4 电流内环的闭环传递函数Gc(z)伯德图Fig.4 Bode plots of transfer function Gc(z) of inner current-loop
2.2 重复控制器外环设计
重复控制器的设计主要包括正反馈回路(重复内模)、周期性延迟环节 Z-N以及校正器(KrZkS(z))的设计。正反馈回路的传递函数为:

其中,Q(z)是衰减滤波器,目的是为了抑制高频领域增益引发的系统不稳定性,通常选为小于1的常数,本文选为0.96。式(5)可表示成如下差分方程形式:

该式表示正反馈回路以电网周期N为步长对误差进行积分,直到误差小于其输出值的4%,而指令的周期重复性与重复控制器前向通道中一个电网周期的延时控制可使系统具有提前控制的能力。这样,重复控制器可类似于PI调节器对直流量进行积分一样对周期性谐波信号进行积分,理论上能够达到几乎无静差的稳态特性效果。若加大Q(z),则可得到更小的稳态误差,但是会降低稳定裕度。
将重复控制器应用于电流环跟踪控制的关键在于前向通道中校正器的设计,其主要是针对电流内环的幅频与相频特性进行设计的,以确保整个系统的稳定运行。校正器中,Kr表示重复控制的增益;Zk表示超前环节,起相位补偿作用;而 S(z)可根据 Gc(z)的特性设计为陷波器或者低通滤波器等。校正器的设计准则是在1.25 kHz(25次谐波)以内的APF补偿范围内使得 ZkS(z)Gc(z)的频率特性校正为 0 dB和0°相位,以保证在足够的稳定裕度前提下获得良好的稳定精度。
由图4分析可知,高频段相位滞后严重难以校正,只有通过衰减高频段的幅值才能不受高频段谐波干扰,因此采用低通滤波器 S(z)对 Gc(z)的高频段幅值进行衰减。S(z)通常选为二阶巴特沃斯低通滤波器,且设计转折频率为3 kHz,阻尼比为0.707,其s域传递函数为:
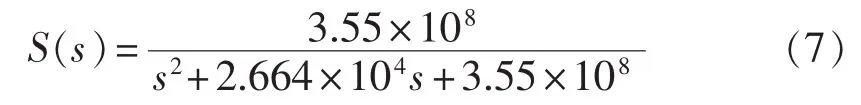
采样频率取18 kHz,经双线性变换法得:

为检验所设计的 S(z)对电流内环 Gc(z)的补偿效果,取 Kr=1,画出 KrS(z)Gc(z)的伯德图,见图 5中实线。

图5 KrS(z)Gc(z)与 Z-3伯德图Fig.5 Bode plots of KrS(z)Gc(z) and Z-3
由图5中实线可以看出电流内环Gc(z)经过校正后的伯德图幅频特性在1.25 kHz以内增益为1,在3 kHz以后开始有明显衰减,至开关频率附近为-60 dB左右,实现了滤波器校正后的高频滤波效果;而从中低频段开始,相角滞后的严重性依旧没有改善,故需加入相位补偿器Zk。Z-3的伯德图如图5中虚线所示,可以看出,在10 Hz~4 kHz的频率范围内 Z-3和 KrS(z)Gc(z)相位上基本一致,而在 4 kHz以上的高频段,由于 S(z)Gc(z)幅值已大幅降低,故而引入的相位滞后不对系统构成稳定性危害。因此,超前环节 Z3可以抵消 KrS(z)Gc(z)带来的相位滞后,使补偿电流可以良好地跟踪指令电流。在实际的程序控制中,考虑到超前环节在DSP中无法表示,一般取Zk-N来代替Zk,即利用DSP控制的存储记忆功能,将滞后第N-k点的重复指令信号保存后来代替超前的第k点的重复指令信号,故Zk取Z3-N。
为验证校正器设计的稳定性,根据小增益原理推导出重复系统稳定的充分条件:
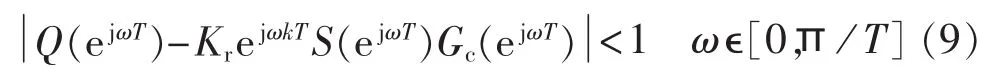
其中,T为采样周期即电网周期。将KrZkS(z)代入,由上文,Q(z)=0.96,k=3,并代入系统其他参数,经运算,式(9)成立,说明校正器设计方案可行。
3 仿真与实验结果分析
对于三相四线制系统,目前常用的2种主电路拓扑为三桥臂分裂电容式[16]和四桥臂式结构。鉴于四桥臂式结构APF比三桥臂分裂电容式APF在主电路中增加了一对桥臂为中线电流提供回路,使控制变得较为复杂且增加成本。本文采取较简单的三桥臂分裂电容式主电路拓扑进行仿真和实验,主电路拓扑见图6。

图6 三桥臂分裂电容式主电路拓扑Fig.6 Topology of main circuit with three bridges and split capacitors
3.1 谐波检测算法仿真结果分析
在MATLAB/Simulink模块中按照图6搭建仿真模型,针对三相四线制不对称阻容负载应用广泛性的特点,负载a、b、c相分别经单相整流桥后接500 μF滤波电容,负载电阻分别为 25 Ω、50 Ω 和 75 Ω,电网线电压为380 V,采样频率为18 kHz。
应用谐波检测算法后的效果见图7,由上至下依次为相负载电流、基波有功电流、无功及谐波电流波形。由图知该算法对a、b两相可提取出各自大小不一的基波有功电流。a、b两相负载电流减去基波有功电流后得到各自的无功及谐波电流。只要能够做到指令电流精确跟踪,便能取得良好补偿效果。

图7 a相和b相各检测电流波形Fig.7 Detected current waveforms of phase a and b
3.2 控制策略仿真结果分析
在APF控制环节仿真的设计中,电压外环的输出作为电容充放有功电流的给定,起到维持直流侧电压稳定的作用,并叠加反向的谐波指令作为前文提到的电流指令。本文仿真直流侧电压给定设为750 V,开关频率为9 kHz,其他控制环参数按照上文分析设计。 仿真中为模拟实际,特别加入 2.8 μs 死区[14],并考虑控制器输出一拍延时。图8为采用传统PI调节器、纯重复控制策略与双环重复控制策略的指令电流跟踪效果对比。图中,曲线1为指令电流波形,曲线2为采用PI调节器的电流跟踪波形,曲线3为采用双环重复控制策略的电流跟踪波形,曲线4为采用纯重复控制策略的电流跟踪波形。

图8 采用各种控制策略的电流跟踪波形对比Fig.8 Comparison of tracking current among different control strategies
由图8中曲线2可以看出,采用传统PI调节器进行电流跟踪虽然能够快速跟踪指令电流,但由于PI调节器无法精确跟踪交流信号以及存在死区和控制器一拍延时的影响,其跟踪的稳态静差较大;由图8中曲线3可以看出,采用双环重复控制策略进行电流跟踪,由于其内环可以对谐波指令做出快速响应,再通过重复控制外环对内环剩余误差进行抑制,只需1个电网周期的动态过程便能实现无静差跟踪,且几乎不受死区和控制器一拍延时输出的影响;由图8中曲线4可以看出,采用纯重复控制策略进行电流跟踪虽然最终可以实现无静差跟踪,但由于周期延迟环节的存在,整个动态过程需要3个电网周期,这点可以从第二个电网周期曲线4与曲线3还存在一定误差看出,但在第三个周期时2条曲线基本趋于一致。
3.3 实验结果分析
对本文提出的谐波检测算法和双环重复控制策略设计实验样机进行实验验证,测得三相电网线电压为 400 V/50 Hz,负载 a、b、c 相分别经单相整流桥后接 500 μF 滤波电容,负载电阻分别为 50 Ω、75 Ω和100 Ω,其余参数同仿真。主控芯片选用TI公司的 DSP芯片 TMS320F2812。使用 HIOKI公司的PW3198电能质量分析仪对实验进行调试和结果记录。
图9由上至下为a相的负载电流、补偿电流和补偿后网侧电流波形;图10由上至下为a、b、c三相不对称阻容负载电流波形;图11由上至下为补偿后a、b、c三相网侧电流波形。

图9 a相各电流波形Fig.9 Current waveforms of phase a
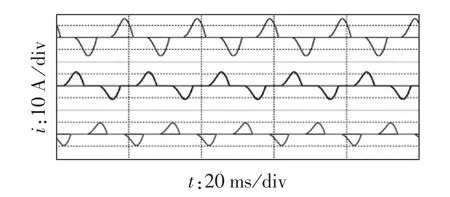
图10 三相负载电流Fig.10 Load current waveforms of three phases
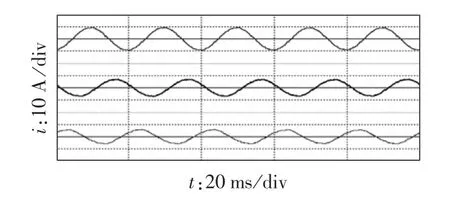
图11 补偿后三相网侧电流Fig.11 Grid-side current waveforms of three phases,with compensation
由图9可以看出,应用本文的谐波检测法和双环重复控制策略可以实现补偿网侧畸变电流的效果,且由于补偿电流能够快速无静差跟踪指令电流,补偿后网侧电流正弦度较好,没有相位偏差导致的缺口或毛刺出现。
对于三相四线制系统,每一相补偿后THD都应达到入网标准规定的5%范围内。由图10可看出,所搭建的三相负载各相大小不等,不对称情形明显,为三相四线制APF提供了恶劣的网侧畸变条件。而由图11可看出,经APF补偿后,三相网侧电流均具有良好的正弦度,波形平滑稳定。经电能质量分析仪检测:a、b、c三相THD分别由补偿前的54.4%、59.2%、65.2%降低至补偿后的2.6%、3.2%、4.4%,达到了入网标准规定要求。
图12为双环控制动态波形,由图可知,采用双环重复控制,当负载突变时,只要1个电网周期就可实现电流跟踪,2个电网周期后即可实现较好的补偿效果。

图12 双环控制动态波形Fig.12 Dynamic waveforms of dual-loop control
4 结语
为增强三相四线制APF的实用性并提高其补偿的快速性和稳态精度,本文对APF谐波检测算法和电流闭环控制算法进行了全面的研究。文中采用的谐波检测算法,可使APF无需补偿基波电流不对称分量,降低了开关器件容量的选取值。将双环重复控制策略应用于三桥臂分裂电容式结构三相四线制APF,仿真和实验验证了该控制策略可快速无静差地跟踪电流指令,且补偿后网侧电流具有较高的波形质量。
参考文献:
[1]PENG F Z,KOHATA M,AKAGI H.Compensation characteristics of shunt and series active filter[C]//Proceedings of 1992 Chinese-Japanse Power Electronics Conference.Beijing,China:[s.n.],1992:381-387.
[2]梁营玉,刘建政,许杏桃,等.基于电源电流和负载电流检测的前馈加反馈的三相四线制APF控制策略[J].电力自动化设备,2015,35(1):94-100.LIANG Yingyu,LIU Jianzheng,XU Xingtao,et al.Feedforwardfeedback control strategy based on detection of power current and load current for three-phase four-wire APF[J].Electric Power Automation Equipment,2015,35(1):94-100.
[3]AKAGIH,KANAZAWA Y,NABAE A.Instantaneousreactive power compensators comprising switching devices without energy storage components[J].IEEE Transactions on Industry Applications,1984,1A-20(3):625-630.
[4]SEBASTIEN M,ALFRED C R.Open loop and closed loop spectral frequency active faltering[J].IEEE Transactions on Power Electronics,2002,17(4):564-573.
[5]刘桂英,粟时平,秦志清.应用多倍频旋转坐标正交变换的三相四线制电路谐波检测方法[J].电网技术,2010,34(7):87-93.LIU Guiying,SU Shiping,QIN Zhiqing.A new harmonic detection method for three-phase four-wire system based on orthogonal transformation of multi-frequency rotating coordinate[J].Power System Technology,2010,34(7):87-93.
[6]黄海宏,刘鑫,薛欢,等.基于载波相移技术的H桥级联高压APF研究[J].电子测量与仪器学报,2012,26(8):687-692.HUANG Haihong,LIU Xin,XUE Huan,etal.Studyofhigh voltage H-bridges cascaded APF based on carrier phase-shift technique[J].Journal of Electronic Measurement and Instrument,2012,26(8):687-692.
[7]陈娟,郑建勇,丁祖军,等.p-q-r法与FBD法在三相四线制系统谐波电流检测中的对比[J].电力自动化设备,2007,27(11):30-33.CHEN Juan,ZHENG Jianyong,DING Zujun,et al.Comparision of harmonic detection in three-phase four-wire system between p-q-r and FBD method[J].Electric Power Automation Equipment,2007,27(11):30-33.
[8]赵伟,王文,肖勇,等.并联有源电力滤波器空间矢量电流控制新方法[J].电力自动化设备,2013,33(8):83-87.ZHAO Wei,WANG Wen,XIAO Yong,et al.Space vector current control of shunt active power filter[J].Electric Power Automation Equipment,2013,33(8):83-87.
[9]侯桂兵,涂春鸣,罗安,等.微电网中APF接入位置与容量优化配置方案[J].电力自动化设备,2012,32(5):29-33.HOU Guibing,TU Chunming,LUO An,et al.Optimal configuration of APF in microgrid[J].Electric Power Automation Equipment,2012,32(5):29-33.
[10]王盼,刘飞,查晓明.基于有源阻尼的并联有源滤波器输出LCL滤波器设计[J].电力自动化设备,2013,33(4):161-166.WANG Pan,LIU Fei,ZHA Xiaoming.Design of output LCL filter based on shunt APF with active damping[J].Electric Power Automation Equipment,2013,33(4):161-166.
[11]TZOU Y Y,OU R S,JUNG S L,et al.High-performance programmable AC power source with low harmonic distortion using DSP-based repetitive control technique[J].IEEE Transactions on Power Electronics,1997,12(4):715-725.
[12]唐健,王翔,何英杰,等.三相四线制有源滤波器的新型无差拍控制[J].电力系统自动化,2007,31(19):59-63.TANG Jian,WANG Xiang,HE Yingjie,et al.A novel deadbeat control scheme for three-phase four-wire active power filters[J].Automation of Electric Power Systems,2007,31(19):59-63.
[13]CASTELLO R C,GRINO R,FOSSAS E.Odd-harmonic digital repetitive control of a single-phase current active filter[J].IEEE Transactions on Power Electronics,2004,19(4):1060-1068.
[14]GRINO R,CARDONER R,COSTA-CASTELLO R,et al.Digital repetitive control of a three-phase four-wire shunt active filter[J].IEEE Transactions on Industrial Electronics,2007,54(3):1495-1503.
[15]ZHOU K L,LOW K S,WANG D W,et al.Zero-phase oddharmonic repetitive controller for a single-phase PWM inverter[J].IEEE Transactions on Power Electronics,2006,21(1):193-201.
[16]周晨,郑益慧,王昕,等.基于双环控制器的电容分裂式三相四线制 DSTATCOM 控制方法[J].电力自动化设备,2014,34(8):114-121.ZHOU Chen,ZHENG Yihui,WANG Xin,et al.Control strategy based on dual-loop controller for split-capacitor-type three-phase four-wire DSTATCOM[J].Electric Power Automation Equipment,2014,34(8):114-121.

