基于BPA数据的交流系统谐波阻抗等值方法研究与应用

吴方劼 ，史梦梦，胡志坚 ，王小飞 ，陈 彬 ，汤 鹏 ，邱骁奇

（1.国网北京经济技术研究院，北京 102209；2.武汉大学 电气工程学院，湖北 武汉 430072）

0 引言

特高压直流输电工程换流站接入系统的边界条件复杂，运行方式多样，合理确定用于交流滤波器设计的谐波阻抗等值参数，能够实现交流滤波器方案的合理配置［1-6］，同时也是研究高压直流输电（HVDC）系统谐波不稳定的关键［7-8］。现代电力系统节点数成千上万，节点方程规模庞大，因而研究一种既能高效处理大型矩阵，又能兼顾考虑电力网络中运行方式变化所引起的网络拓扑结构变化的谐波阻抗计算方法显得尤为重要。

加拿大太西蒙公司开发的NIMSCAN程序是目前世界上使用最广泛的谐波阻抗等值程序，该程序通过扫描BPA数据对系统阻抗进行计算，但扫描过程过于繁琐［9］，且没有核心源代码，特别是随着电网电压等级的增加、新元件的出现，现有计算平台无法有效应对后续的模型升级，已越来越不适应现代系统的计算。因此，开发符合我国实际电网的谐波阻抗计算软件十分必要，对实现我国直流输电工程自主化设计具有重要意义［10］。

文献［11］研究推导了变压器、发电机的数学模型，但没有对整个系统的等值做进一步研究。文献［9，12-13］给出了计算谐波阻抗的方法，却没有研究开断线路的影响，也缺少对某一特定频次下系统阻抗的分析。在滤波器设计中，需要提供观察点在各种不同运行方式下的阻抗扫描范围。文献［14］推导了稀疏矩阵的LU分解公式，但没有针对电力系统中导纳矩阵的对称性进行细化研究。文献［15-16］介绍了传统的节点导纳矩阵的生成方法，文献［17］采用邻接矩阵表示设备与进出线之间的连接关系，本文将该方法进行了改进，得到连线矩阵，应用于节点编号优化和节点导纳矩阵的形成，以减小程序的计算量。

本文基于BPA数据［18］，采用电力系统各元件典型谐波模型［19］，由改进的节点法得到导纳矩阵Y，根据YV=I，由单位电流注入法，计算得到V，即所需节点的等值谐波阻抗。为充分利用节点导纳矩阵的稀疏特性，减少不必要的计算以提高求解效率，本文提出基于半动态-遗传算法的节点编号优化方法，并采用排零存储和排零运算技术［20］进一步提高谐波阻抗计算程序的运行速度。对标准IEEE 9节点系统进行计算，将计算结果与该系统在PSCAD下的仿真结果进行对比分析。同时对湖南长沙特高压直流工程进行谐波阻抗计算，得到其可能发生的谐振频次，接着计算了该频次所有运行方式下±20 Hz范围内的阻抗值，得到该频次下的阻抗包络图，以此作为该直流工程滤波器调谐点和参数设计的输入条件。

1 元件的谐波阻抗模型

进行谐波分析时，准确的元件模型是保证获得精确、可靠结果的关键因素。在研究BPA中元件模型的基础上，参考各种典型的元件谐波阻抗模型，采用的元件模型如下。

1.1 同步发电机

忽略集肤效应对电阻的影响，采用发电机次暂态电抗。等值电路如图1所示。

发电机h次谐波下的阻抗表达式为：

图1 发电机等值电路Fig.1 Equivalent circuit of generator

其中，Ra为发电机电枢电阻；Xd″为发电机在基频下的次暂态电抗；h为谐波次数。

1.2 变压器

变压器π型等值电路如图2所示，与发电机相同，忽略集肤效应的影响，h次谐波下变压器阻抗可以用式（2）统一表达：

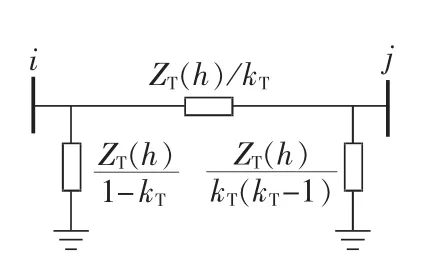
图2 变压器π型等值电路Fig.2 Equivalent pi circuit of transformer

其中，RT为变压器短路电阻；XT为变压器短路电抗。图2中kT为变压器变比。

1.3 输电线路

由于BPA中线路给出的是集中参数数据，故在计算等值阻抗时，输电线路也采用集中参数模型，如图3所示。图中，RL为线路总电阻；XL为线路总电抗；B1为线路i端电纳；B2为线路j端电纳。

B1=B2时，为对称线路；B1≠B2时，为不对称线路。

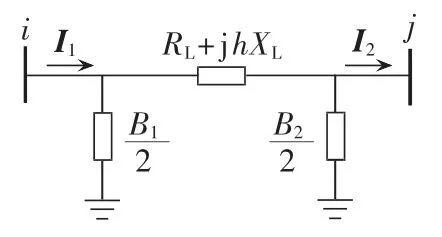
图3 输电线路模型Fig.3 Transmission line model

1.4 负荷

BPA潮流数据中负荷模型是已知负荷吸收功率的，电网中绝大部分负荷是集中负荷，并联负荷模型适合用于表示集中负荷。等值模型如图4所示。图中，RP和XP分别为负荷的等效电阻和等效电抗；P和Q分别为该处母线吸收的有功和无功功率；UP为该处的电压值。导纳YP（h）随Q的不同而有所不同，计算公式如下。

a.无功功率Q为正时，为感性负荷，此时有：

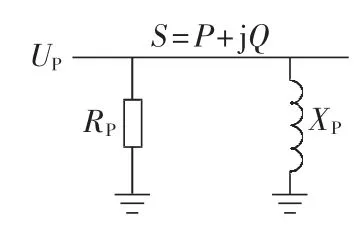
图4 负荷模型Fig.4 Load model

b.无功功率Q为负时，为容性负荷，此时有：

1.5 并联电容组

实际情况中，大容量无功补偿装置不作为负载，而是从负载中分离出来作为单独的支路进行处理。

已知额定容量为QC，额定电压为UC时，有：

其中，XC为容性电抗；QC单位为Mvar；UC单位为kV。

2 基于半动态-遗传算法的节点编号优化

2.1 半动态-遗传算法

在对网络节点进行编号优化时，半动态法以其简单易行、效果良好而得到广泛应用，但存在局部寻优、搜索方式单一等固有缺陷。遗传算法具有随机搜索、全局最优的优点［21］。本文将这2种方法结合，针对电力系统节点编号的特点，综合2种算法的优点，用于编号优化。其在优化效果上优于半动态法，在运行时间上优于遗传算法。

半动态-遗传算法的具体实现步骤如下：

a.因为消去出线度为1的节点不产生非零注入元，首先用半动态法消去出线度为1的节点；

b.在步骤a执行完毕后，节点之间连接关系发生变化，更新连线矩阵，若仍存在出线度为1的节点，继续执行步骤a，否则执行步骤c；

c.在步骤a、b执行完后，剩余的节点出线度均大于1，用遗传算法对出线度最少的所有节点进行选择、交叉、变异操作，得到最优编号；

d.重复执行步骤a、b、c，直到所有节点均被消去。

半动态-遗传算法流程图如图5所示。

图5 半动态-遗传算法流程图Fig.5 Flowchart of semi-dynamic genetic algorithm

2.2 优化目标函数

假设在节点消去的过程中，直接与节点k相连的节点数为Nk，这Nk个节点之间已经有Dk条支路。当节点k被消去时，增加的支路数，即新引入的非零元素数Δbk为：

若网络有n个节点，则编号优化目标函数为：

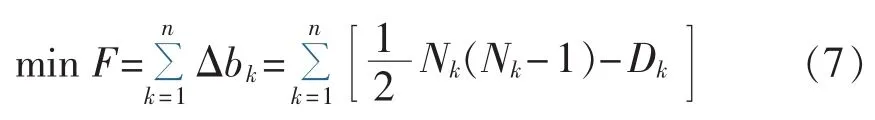
其中，每个节点的Nk和Dk将随着附近节点的消去而变化，应及时更新。

为此，本文程序采用连线矩阵M，其结构见式（8）。

连线矩阵表示节点之间的连接关系，一共有3列，前2列表示节点编号，第3列表示这2个节点所在的支路编号。例如式（8）第1行表示节点1和2相连，支路编号为1；最后1行表示节点p和q相连，支路编号为s。

3 导纳矩阵的形成及求解

3.1 改进的节点法

上文介绍的连线矩阵M包含了系统的支路连接信息，故用节点法形成导纳矩阵时，利用矩阵M改进传统节点法的操作，以提高程序的运行效率。

在形成M时，本文的改进方法是：依次扫描BPA数据中对称线路（LN）、不对称线路（EN）和变压器（T），设其数量分别为 nL、nE和nT，则连线矩阵第 3列的支路编号1—nL表示连接两节点的是LN，编号nL+1—nL+nE表示 EN，编号 nL+nE+1—nL+nE+nT表示T。根据M第3列可确定各节点所连支路类型，从而形成该节点的互导纳和部分自导纳，再扫描该节点连接的发电机、负荷等接地元件，即得到剩余部分自导纳值。形成每个节点导纳的流程图见图6。

图6 节点导纳矩阵形成流程图Fig.6 Flowchart of node admittance matrix formation

根据优化编号后的节点顺序，依次得到每个节点的导纳，最终得到整个系统的导纳矩阵。

在谐波阻抗等值计算中，往往还要考虑不同运行方式下的等值情况。例如，切除某电力线路或变压器。由于改变一个元件的参数或它的投入、退出只影响该支路两端节点的自导纳和它们之间的互导纳，可不必重新形成与新运行状况相对应的节点导纳矩阵，仅需对原有的矩阵作某些修改。

切除一条导纳为yij的支路相当于增加一条导纳为-yij的支路，与节点i、j有关的元素作如下修改：

至此，得到N-0、N-1及N-2方式下系统的导纳矩阵，可以计算在这3种方式下的等值阻抗。

3.2 LU分解及前代回代

由于导纳矩阵Y是一个对称矩阵，得到其上三角部分数据即可得到整个导纳矩阵数据。在本程序中，Y是逐行形成的且只求取其上三角部分数据，同时逐行进行分解。假设导纳矩阵第i行元素为Yi=［0 0 … yiyi＋1… yn］，上三角矩阵的第 i行为 Ui=［0 0 … uiui＋1… un］，下三角矩阵的第 i列为 Li=［0 0 … 1 li＋1… ln］T。 采用的LU分解公式如下：

其中，yj、uj对应矩阵Y和矩阵 U第i行的第j个元素；lj对应矩阵L第i列的第j个元素。

节点电压方程YV=I的矩阵形式如下所示：

将Y进行LU分解后，矩阵方程YV=I转化为LUV=I，令UV=X，有LX=I。求解网络节点方程分为2步：前代，求解LX=I，计算出X；回代，求解UV=X，得到需要的V。

交流系统谐波阻抗计算流程图如图7所示。

4 IEEE 9节点系统算例

以标准IEEE 9节点电力系统为算例，利用电力系统电磁暂态仿真软件PSCAD的谐波分析功能对本文方法进行验证。

图7 谐波阻抗计算流程图Fig.7 Flowchart of harmonic impedance calculation

IEEE 9节点系统PSCAD仿真示意图如图8所示。图中，发电机、变压器均采用PSCAD简化模型，输电线路采用π型电路，S1—S4为4个母线负荷，采用Fixed Load模型，QC1—QC3实现无功补偿的功能。在无直流输电的情况下，利用PSCAD中的Z（f）工具可以方便地对系统进行谐波阻抗扫描，扫描范围设置为 50～2500 Hz。

利用本文提出的半动态-遗传算法对系统进行节点编号优化，可快速得到最优编号方案，在此仅在表1中列出3种最优方案。分析结果可以看出，完成最优编号最少要注入3个非零元素。

表1 IEEE 9节点系统编号优化Table 1 Optimal node numbering schemes of IEEE 9-bus system

选择BUS2作为观察点，扫描1～50次谐波下的阻抗。2种方法的计算结果如表2所示。

由表2可以看出，本文方法计算得到的IEEE 9节点阻抗值和用PSCAD仿真得到的节点阻抗值偏差很小，验证了本文方法的正确性和有效性。

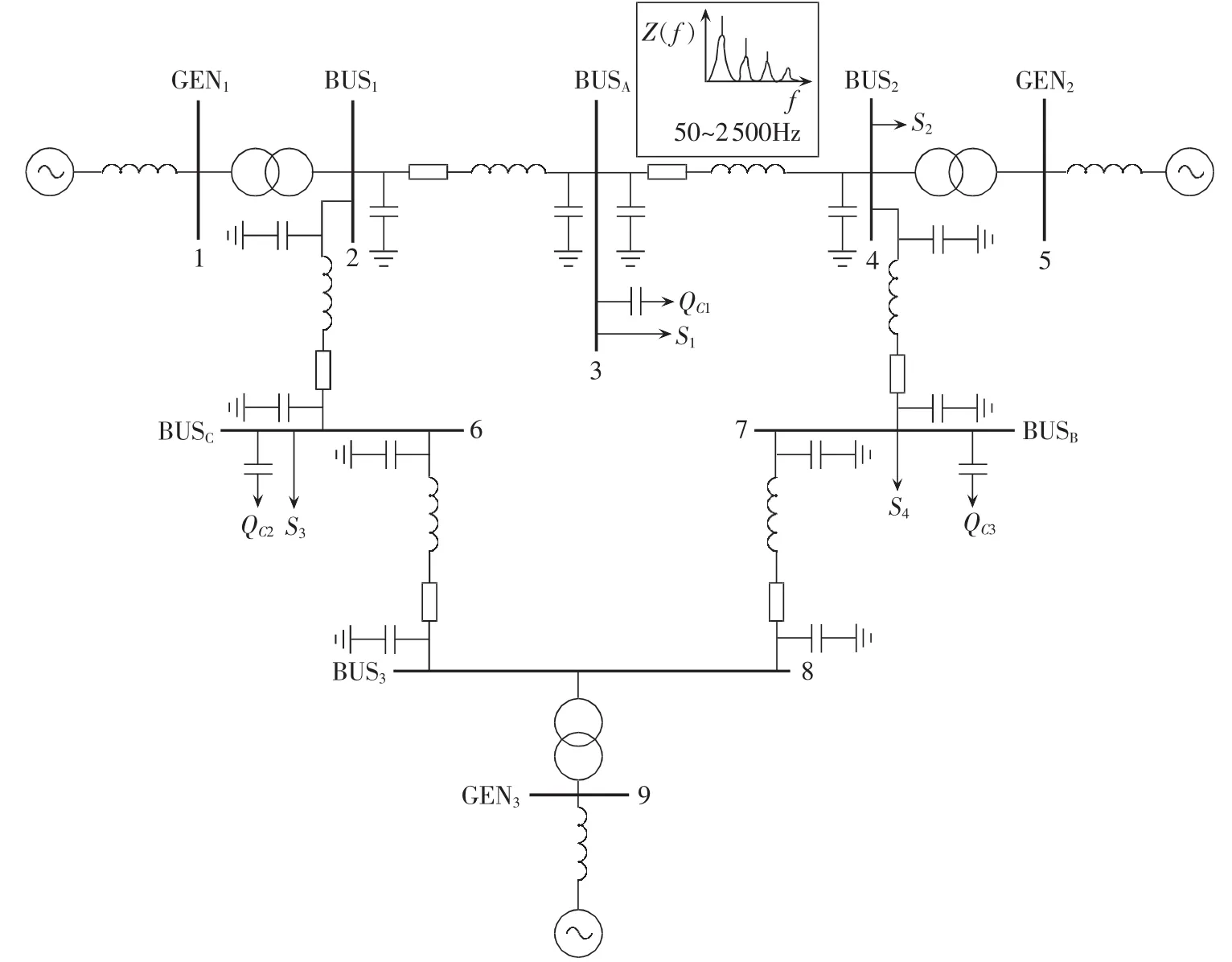
图8 IEEE 9节点系统Fig.8 IEEE 9-bus system

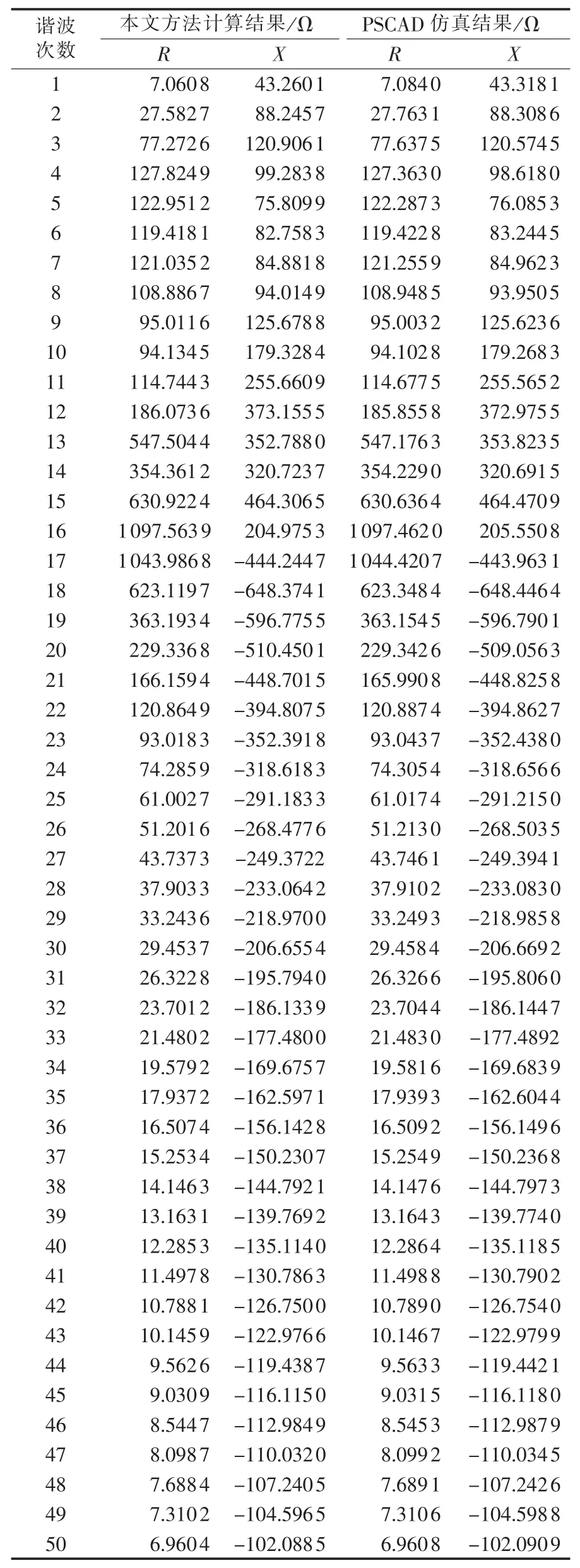
表2 本文方法计算结果与PSACD仿真结果对比Table 2 Comparison of calculative results between proposed method and PSACD simulation

从以上分析可知，PSCAD的谐波扫描工具使用方便，对节点数较小的系统可以进行精确的仿真，然而当系统较大时，手动搭建模型不仅工作量大而且可能出现人为误差［22］。本文提出的数值计算方法，以已有的BPA数据为依托，不必搭建庞大的模型，且在计算速度上要优于仿真。

5 湖南长沙特高压直流工程计算结果

以湖南长沙特高压直流输电工程2015年度基本潮流数据为依托，对丰大、丰小、枯大、枯小4种运行方式，N-0、N-1、N-2 3种线路开断方式分别进行了计算。该工程在丰大时有537条母线、102台发电机、241台变压器、82条不对称线路、575条对称线路。以换流站为中心的直流输电系统拓扑结构如图9所示。

图9中，虚线框内为直流输电部分，包括换流站和直流输电线路；左右两端交流系统各用戴维南电路等效为一个带阻抗的发电机。选择第一个出线母线为观察点，即图中的母线JQDC。

5.1 节点编号优化结果比较

计算机硬件配置为Pentium G2030，CPU主频3.0 Hz，内存 2 GB，操作系统 Windows 7，仿真环境VC6.0。分别用静态法、半动态法、遗传算法、半动态-遗传算法对该工程进行编号优化，比较其新增支路数及完成编号所用时间，结果如表3所示。

表3 不同优化算法所用时间对比Table 3 Comparison of calculation time among different optimization algorithms

由优化结果可以看出，遗传算法的新增支路数适中，用时较长；半动态法的新增支路数不是最优；半动态-遗传学算法新增支路数最少，用时介于半动态法和遗传算法之间。对于同一个系统，节点编号只需一次，下次计算可直接调用，故这里对编号优化用时不做严格要求。

对该工程深入分析发现，537条母线中，出线度为1的母线有238条，占总母线数的44.3%。将这类节点用半动态法消去，可以极大减轻编号优化的工作量。

5.2 不同运行方式下阻抗计算结果

对湖南地区的丰大、丰小、枯大、枯小4种运行方式，在N-0、N-1、N-2下的工况进行计算分析，选择母线JQDC为观察点，N-1断开母线JQDC与X03xtG所连线路，N-2在N-1的基础上断开母线JQDC与X02zznG所连线路。频率范围为50～2500 Hz，扫描步长为5 Hz，限于篇幅，本文只给出丰大方式下的计算结果。

丰大N-0方式下的阻抗图与幅频特性图分别如图10和图11所示。

图9 直流输电系统拓扑结构图Fig.9 Topology of HVDC system

图10 丰大N-0方式下的阻抗图Fig.10 Impedance diagram in flood season large power flow mode of N-0 pattern

图11 丰大N-0方式下的幅频特性图Fig.11 Impedance-frequency chart in flood season large power flow mode of N-0 pattern

丰大N-1方式下（断JQDC与X03xtG所连线路）的阻抗图与幅频特性图分别如图12和图13所示。

丰大N-2方式下（断JQDC与X03xtG所连线路及JQDC与X02zznG所连线路）的阻抗图与幅频特性图分别如图14和图15所示。

由以上阻抗图及幅频特性图可以得到在JQDC处，不同的运行方式下阻抗的分布情况及可能发生的谐振点，从而为JQDC节点处的滤波器参数设计提供了依据。

图12 丰大N-1方式下的阻抗图Fig.12 Impedance diagram in flood season large power flow mode of N-1 pattern

图13 丰大N-1方式下的幅频特性图Fig.13 Impedance-frequency chart in flood season large power flow mode of N-1 pattern

图14 丰大N-2方式下的阻抗图Fig.14 Impedance diagram in flood season large power flow mode of N-2 pattern

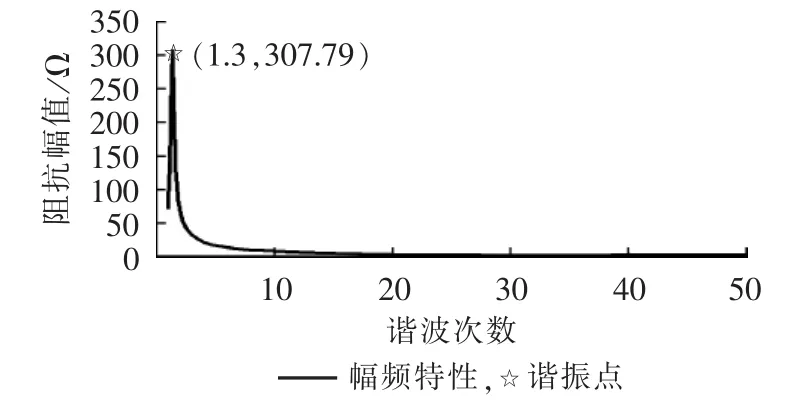
图15 丰大N-2方式下的幅频特性图Fig.15 Impedance-frequency chart in flood season large power flow mode of N-2 pattern

5.3 考虑某一特定频次下的阻抗结果

为了考虑某一节点的某一特定频次作为直流工程滤波器调谐点和参数设计的输入条件，需要得到所有运行方式下该频次的阻抗值。由5.2节的结果可以看出，在3次谐波附近容易发生谐振，对电网危害极大。选择母线JQDC为观察点，计算丰大、丰小、枯大、枯小分别在N-0、N-1、N-2运行方式下3次谐波及其±20 Hz范围内的阻抗值，得到其扇形包络图如图16所示。

图16 3次谐波在所有方式下扇形包络图Fig.16 Fan-shaped envelope diagram for third harmonic in all modes

由图16得到，阻抗值的最小相角为-88.01°，最大相角为33.16°，同时得到最大、最小相角对应的阻抗值。从而得到母线JQDC处3次谐波作为直流工程滤波器调谐点和参数设计的输入条件。

6 结论

本文提出了基于中国版BPA数据的电力系统谐波阻抗等值计算方法，通过PSCAD验证了本文方法的正确性。采用本文方法对湖南长沙特高压直流工程的谐波阻抗进行了等值计算，得到了在换流站（JQDC）处作为直流工程滤波器调谐点和参数设计的输入条件，为JQDC节点处的滤波器参数设计提供了依据。该方法具有普适性，弥补了现有谐波阻抗等值程序的不足，能满足现代电力系统谐波阻抗等值计算要求。

［1］舒印彪，刘泽洪，高理迎，等.±800 kV 6400 MW特高压直流输电工程设计［J］.电网技术，2006，30（1）：1-8.SHU Yinbiao，LIU Zehong，GAO Liying，etal.A preliminary exploration for design of±800 kV UHVDC project with transmission capacity of 6400 MW［J］.Power System Technology，2006，30（1）：1-8.

［2］邓旭，王东举，沈扬，等.±1100kV特高压换流站直流操作过电压研究［J］.电力自动化设备，2014，34（1）：141-147.DENG Xu，WANG Dongju，SHEN Yang，etal.DC switching overvoltage of ±1100 kV UHVDC converter station［J］.Electric Power Automation Equipment，2014，34（1）：141-147.

［3］马为民，聂定珍，曹燕明.向家坝—上海±800 kV特高压直流工程中的关键技术方案［J］.电网技术，2007，31（11）：1-5.MA Weimin，NIE Dingzhen，CAO Yanming.Key technical schemes for ±800 kV UHVDC project from Xiangjiaba to Shanghai［J］.Power System Technology，2007，31（11）：1-5.

［4］郭贤珊，马为民.向家坝—上海±800 kV特高压直流示范工程的低频谐振分析［J］.电网技术，2008，32（10）：1-10.GUO Xianshan，MA Weimin.Analysis on low frequency resonance in±800 kV UHVDC demonstration project from Xiangjiaba to Shanghai［J］.Power System Technology，2008，32（10）：1-10.

［5］邓旭，王东举，沈扬，等.±1100 kV准东—四川特高压直流输电工程主回路参数设计［J］.电力自动化设备，2014，34（4）：133-140.DENG Xu，WANG Dongju，SHEN Yang，etal. Main circuit parameter design of Zhundong-Sichuan±1100 kV UHVDC power transmission project［J］.Electric Power Automation Equipment，2014，34（4）：133-140.

［6］杨志栋，李亚男，殷威扬，等.±800kV向家坝—上海特高压直流输电工程谐波阻抗等值研究［J］.电网技术，2007，31（18）：1-4.YANG Zhidong，LI Yanan，YIN Weiyang，et al.Study on harmonic impedance equivalents used for AC filter design of±800 kV UHVDC transmission project from Xiangjiaba to Shanghai［J］.Power System Technology，2007，31（18）：1-4.

［7］王钢，李志锵，李海锋，等.HVDC换流器等值谐波阻抗的计算方法［J］.中国电机工程学报，2010，30（19）：64-68.WANG Gang，LI Zhikeng，LI Haifeng，et al.Calculation method of harmonic equivalent impedances of HVDC converter［J］.Proceedings of the CSEE，2010，30（19）：64-68.

［8］马玉龙，肖湘宁，姜旭，等.HVDC换流器的阻抗频率特性［J］.电力系统自动化，2006，30（12）：66-69.MA Yulong，XIAO Xiangning，JIANG Xu，et al.Study on impedancefrequency characteristic on HVDC converters［J］.Automation of Electric Power Systems，2006，30（12）：66-69.

［9］段慧.交流系统谐波阻抗等值与背景谐波分析［D］.杭州：浙江大学，2008.DUAN Hui.The AC system harmonic impedance equivalence and background harmonic analysis［D］.Hangzhou：Zhejiang University，2008.

［10］常浩，樊纪超.特高压直流输电系统成套设计及其国产化［J］.电网技术，2006，30（16）：1-5.CHANG Hao，FAN Jichao.System design and its localization of UHVDC transmission project［J］.Power System Technology，2006，30（16）：1-5.

［11］韩俊，徐韬，王峰，等.电力滤波器设计软件的开发和应用［J］.中国电力，2010，43（8）：46-50.HAN Jun，XU Tao，WANG Feng，etal. Developmentand application of power filter design software ［J］.Electric Power，2010，43（8）：46-50.

［12］DE OLIVEIRA A，DE OLIVEIRA J C，RESENDE J W，et al.Practicalapproaches for AC system harmonic impedance measurements［J］.IEEE Transactions on Power Delivery，1991，6（4）：1721-1726.

［13］DENSEMTJ，BODGER PS，ARRILLAGA J.Threephase transmission system modelling for harmonic penetration studies［J］.IEEE Transactions on Power Apparatus and Systems，1984（2）：310-317.

［14］徐晓飞，曹祥玉，姚旭，等.一种基于Doolittle LU分解的线性方程组并行求解方法［J］.电子与信息学报，2010，32（8）：2019-2022.XU Xiaofei，CAO Xiangyu，YAO Xu，etal.Parallelsolving method of linear equations based on Doolittle LU decomposition［J］.Journal of Electronics&Information Technology，2010，32（8）：2019-2022.

［15］谭李师.基于母线的节点导纳矩阵计算机生成方法［J］.电力建设，2008，29（4）：92-94.TAN Lishi.Generation method of bus node admittance matrix based on computer［J］.Electric Power Construction，2008，29（4）：92-94.

［16］何仰赞，温增银.电力系统分析［M］.华中科技大学出版社，2002：70-76.

［17］陈晨，刘俊勇，刘友波，等.一种考虑变电站内部的电力系统可靠性分析［J］.电力自动化设备，2015，35（2）：103-109.CHEN Chen，LIU Junyong，LIU Youbo，etal.Powersystem reliability analysis considering substation interior［J］.Electric Power Automation Equipment，2015，35（2）：103-109.

［18］中国电力科学研究院.PSD-BPA潮流程序用户手册［M］.北京：中国电力科学研究院，2007：68-85.

［19］STEVENSON W D.Elements of power system analysis［M］.New York，USA：McGraw-Hill，1982：47-84.

［20］TINNEY W F，WARLKER J W.Direct solutions of sparse network equations by optimally ordered triangular factorization［J］.Proceedings of the IEEE，1967，55（11）：1801-1809.

［21］罗军，于歆杰.基于遗传算法的稀疏节点优化编号方法［J］.电网技术，2006，30（22）：54-58.LUO Jun，YU Xinjie.Sparsity node ordering technology based on genetic algorithms［J］.Power System Technology，2006，30（22）：54-58.

［22］陶华，许津津，邹文聪.BPA向PSCAD模型转换的研究［J］.电力自动化设备，2013，33（8）：152-156.TAO Hua，XU Jinjin，ZOU Wencong.Model conversion from BPA to PSCAD［J］.Electric PowerAutomation Equipment，2013，33（8）：152-156.