使用GA初始化CGHMM参数的轴承故障诊方法

陆汝华，颜文燕(湘南学院软件与通信工程学院，湖南郴州423000)



使用GA初始化CGHMM参数的轴承故障诊方法

陆汝华，颜文燕
(湘南学院软件与通信工程学院，湖南郴州423000)

摘要：连续高斯混合密度隐马尔可夫模型（ContinuousGaussian MixtureHidden Markov Model, CGHMM）在故障诊断领域得到了广泛应用，取得了较好效果。CGHMM训练模型较大、局部最优，但模型参数初始化值会直接影响迭代收敛速度和模型效用。全局最优的遗传算法（GeneticAlgorithm, GA）初始化CGHMM模型参数，为CGHMM训练提供了一个好的初始值，不仅可以加快收敛速度，还可以得到一个更好的模型。通过GA初始化CGHMM、CGHMM训练和CGHMM诊断过程等三个方面的仿真实验和比较分析可以得出，该方法具有训练速度快和CGHMM模型好的优点。在最后的CGHMM诊断仿真实验中，该方法诊断精度为100%，高于经典方法的96%，表明GA确实可以成功应用于CGHMM参数初始化，是一种可行的故障诊断方法。

关键词：振动与波；遗传算法；初始化；连续高斯混合密度隐马尔可夫模型；故障诊断

在旋转机械设备中，滚动轴承是应用最为广泛、同时也是最重要的部件之一，其运行状态好坏直接影响整个设备的性能、寿命、功能和效率，如果滚动轴承发生故障，往往会导致异常噪声和振动，严重时还会损坏设备，造成工业生产效率下降，甚至带来严重事故和安全问题[1]，因此，对滚动轴承进行在线监测与故障诊断，及时准确检测出轴承工作状态具有十分重要的应用价值和意义[2]。在这种背景环境中，如何针对滚动轴承的微弱故障特征进行故障诊断是成为机械领域的热点和难点问题之一[3]。

故障诊断实质上是一个模式识别过程，近年来，学者们相继提出各种故障特征分类有效方法，除了神经网络和支持向量机等之外，研究数量较多、性能效果较好的还有隐马尔可夫模型(Hidden Markov Model，HMM)[4]。HMM分为离散HMM（DHMM）和连续HMM（CHMM），基于高斯密度混合函数的CHMM又称为CGHMM。与DHMM相比，CGHMM涉及到更为复杂的数学模型，能够得到更高的诊断精度，当然是以运算速度作为代价。也正因为如此，学者对CGHMM方法进行了多种改正，尤其是在HMM训练算法中对HMM参数的初始化问题上面。对于数据量大的CGHMM而言，随机初始化导致训练算法的迭代过程很难收敛，不仅造成训练时间的延长，不停的数据运算也会降低数据精度，因而出现了使用聚类算法等初始化方法[5]。但HMM训练算法（经典的Baum-Welch算法）只是一种局部最优的梯度下降算法，在训练过程中存在陷入局部的缺点，而遗传算法(Genetic algorithm，GA)可以克服这个缺陷[6]。因此，作者利用GA的全局搜索能力优化CGHMM训练过程，得到全局最优的CGHMM模型。最后仿真实验中的各种实例验证了该方法的有效性，为轴承故障诊断提供了一种新方法。

1　CGHMM训练模型

CGHMM模型包括初始概率分布π，状态转移概率A和观察值概率B，而B=(μ，σ2，ω)又由均值矢量μ、协方差矩阵σ2和权值ω三个参数组成，可以说CGHMM模型包含五个参数，记为λ=(π，A，μ，σ2，ω)。对CGHMM模型进行训练，即CGHMM五个参数π、A、μ、σ2、ω的迭代重估过程，通常采用Baum-Welch算法[7]。首先是输入一系列观察值，并初始化五个参数值π、A、μ、σ2、ω，再根据CGHMM训练算法不断迭代获得新的模型参数，使输出概率P(O/λ)达到最大[7]。

CGHMM参数可以采取随机初始化方法，不过会造成很多次的迭代才能收敛，这样不仅增长训练运行时间，也会降低数据运算精度。有不少研究者提出采用k-means聚类算法进行初始化，这样基于观察值序列的初始化会使初始模型来源于样本数据，在一定程度上优化训练算法。但是，由于CGHMM是一个含有隐变量的统计模型，在Baum-Welch迭代重估过程中存在陷入局部的缺点，只能找到一个局部最大的输出概率P(O/λ)，也就是局部最优的CGHMM参数π、A、μ、σ2、ω。GA算法依据自然界适者生存、优胜劣汰的进化机制来搜索和计算问题最优解，主要特点是群体搜索策略和群体中个体之间的信息交换，搜索不依赖于梯度信息[8]，因此，使用GA初始化CGHMM参数进行CGHMM训练，以达到全局最大的输出概率P(O/λ)，获得全局最优的CGHMM模型，以便在轴承故障诊断过程中能够得到更好的诊断效果。

2　GA初始化CGHMM参数的改进算法

GA是全局最优的搜索算法，当确定个体组成的种群之后，使用适应度函数通过一系列选择、交叉、变异等操作获得最优的个体[9]，详细算法流程如图1所示。

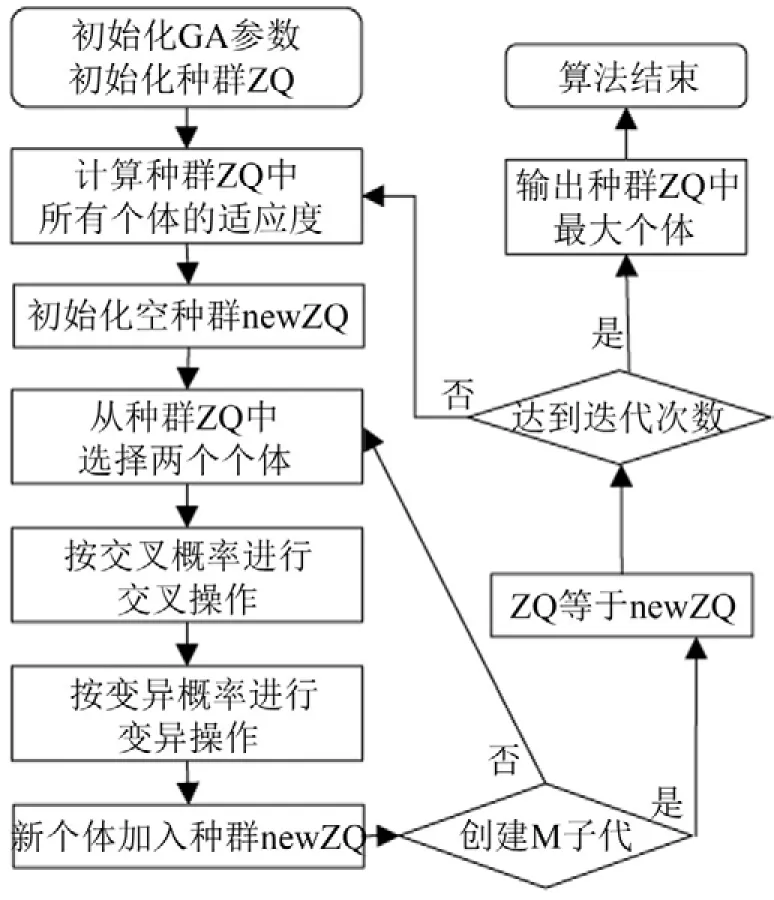
图1　遗传算法流程图

在图1所示流程图中，GA初始化CGHMM参数主要包括如下几个步骤。

（1）个体的定义与组成结构

在CGHMM初始模型中，π、A的选取对模型性能影响不大，可以随机初始化，这里只考虑GA初始化其它三个参数μ、σ2、ω，获得参与CGHMM训练的初始模型。但不可将μ、σ2、ω三个参数作为个体，不仅是因为三类组成个体增加程序的复杂性，还因为这三者之间存在一定关联，并不是独立无关的三个变量。也不能将CGHMM模型中的B作为个体，因为在CGHMM模型中，B又是由三个参数μ、σ2、ω组成，通过GA算法之后即使获得了B值，也无法分别确定μ、σ2、ω的值。考虑到三个参数μ、σ2、ω可通过观察值序列计算得出，因此定义观察值序列为个体，获得最优个体之后，再根据最优个体计算出μ、σ2、ω三个参数的值，得到最优的CGHMM初始模型。

不过，GA算法输出的最优个体只是一串二进制符号，需要确定个体组成才能知道如何参与运算。而个体组成与原始信号特征提取有关，记观察值序列长度为T，MFCC特征提取维数为L，每一个浮点数对应的二进制位数为M，个体的组成结构如图2所示，可以看出，一个个体包括T×L×M位二进制码。

图2　个体的组成结构

（2）个体适应度函数定义

适应度是生物学中用于表示物种对生存环境适应的程度，在GA中是选择和评价个体的依据。CGHMM模型的好坏取决于输出概率P( O/λ)是否尽可能最大，O是输入的观察序列样本，λ是CGHMM训练的初始模型，其中μ、σ2、ω参数由GA获得的个体分别计算得出的均值、方差和权值。以多样本观察序列为CGHMM训练数据，记为，N为样本数，则定义个体适应度函数为

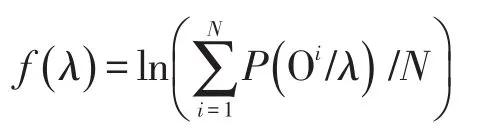
（3）遗传算子

遗传算子包括选择、交叉、变异等基本操作，在算法中执行的次数是迭代次数乘以遗传代数。

选择操作使用通常的轮盘赌算法，从已有的种群中根据概率选择一些个体来产生下一代，而这个概率与个体的适应值函数成正比关系。设种群中个体数为n，个体i的适应度函数为Fi，个体i被选择的概率为Pi，则存在下列比例关系

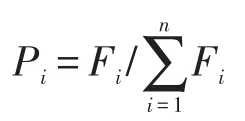
从种群ZQ中选择一个个体的基本步骤分为四步。

Step2:产生一个0到sum之间的随机数；

Step 3:将种群ZQ中所有个体根据适应度大小值从小到大排序；

Step 4:从种群ZQ中第1个个体开始，将适应度值与后面个体的适应度值依次相加，直到累加和大于等于sum，最后一次加进去的个体即为选择的新个体。

对选择之后的个体按交叉概率Pc执行交叉操作，通过两个父代的部分结构加以替换组成新的个体，是获取优秀个体最重要的步骤，GA的搜索能力得以飞跃性提高。由于CGHMM模型中个体的复杂性和个体间线性关系的特殊性，需要通过线性组合完成交叉。设线性组合系数为λ1和λ2，个体Oi和Oj的交叉公式为

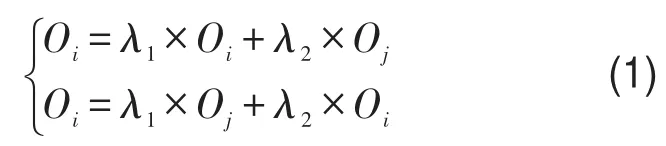
交叉之后的新个体按变异概率Pm随机生成几个位置点对父代执行变异操作，以便繁殖更优秀的后代，获得更优的个体，同时也保持了种群中个体的多样性。

（4）获得新种群

种群通过随机初始化获得多个个体，但经过选择、交叉、变异等操作多次循环之后的新种群并不一定优于旧种群，为了让每次繁殖至少不会降低最大适应度，最确定新种群之前，先判断旧种群的最大个体适应度是否大于新种群的最大个体适应度，如果是，则将旧种群最大适应度对应的个体替换新种群中最小适应度对应的个体，以保证新种群最大个体适应度只增不减。

3　故障诊断仿真实验

3.1仿真实验准备

（1）数据准备

在CGHMM训练与诊断中，所使用的原始数据是6202 CM深沟球滚动轴承，在转速为1 800 r/min运行速度下采集的音频信号。然后将音频信号进行预处理，划分为256帧长的多段部分重叠帧、12维MFCC进行特征参数提取，最后得到长度36的观察值序列。采集的数据包括轴承正常音、内圈异音、外圈异音、滚动体异音、保持架异音等五种工作状态下的音频信号各50个，每一种的前20个作为CGHMM训练样本，后30个用于CGHMM故障诊断测试。

（2）参数设置

通过不断反复实验，采用自编程序测试不同参数设置的诊断效果，最后得到一组效果最好的参数值。在GA中，种群中个体数为50，因为MFCC参数绝对值最大数在500以内，因此浮点数转换为二进制串的位数为9，最重要的两个参数交叉概率和变异概率分别为0.88和0.02。在CGHMM模型中，状态数设置为7，混合高斯数设置为3，以完成CGHMM训练和故障诊断实验。

3.2 GA初始化CGHMM实验

实验采用的GA包括两种方法，方法一：个体选择三个参数μ、σ2、ω随机初始化种群，经过选择、交叉、变异等操作之后获得新种群；方法二：个体定义为观察值序列O，经过选择、交叉、变异等操作之后，再从旧种群最大适应度和新种群最小适应度中的较大者选择，以获得新种群。都以种群内最大适应度变化很小为收敛条件，两种方法各自运行50次的繁殖代数实验结果比较如表1所示。从繁殖代数的最大值、最小值和平均值可以说明，方法二的收敛速度远远快于方法一。

表1　遗传算法繁殖代数

为了能够直观显示迭代过程，方法一与方法二都选取一次繁殖代数接近平均值的实验，每一次繁殖之后获得的种群最优适应度和平均适应度如图3所示。从图中可以得出，方法二的最优适应度和平均适应度都高于方法一，并且，方法二的曲线变化更加平滑，基本是一直上升，50次迭代即达到收敛条件，这也正说明了利用GA初始化CGHMM的有效性。

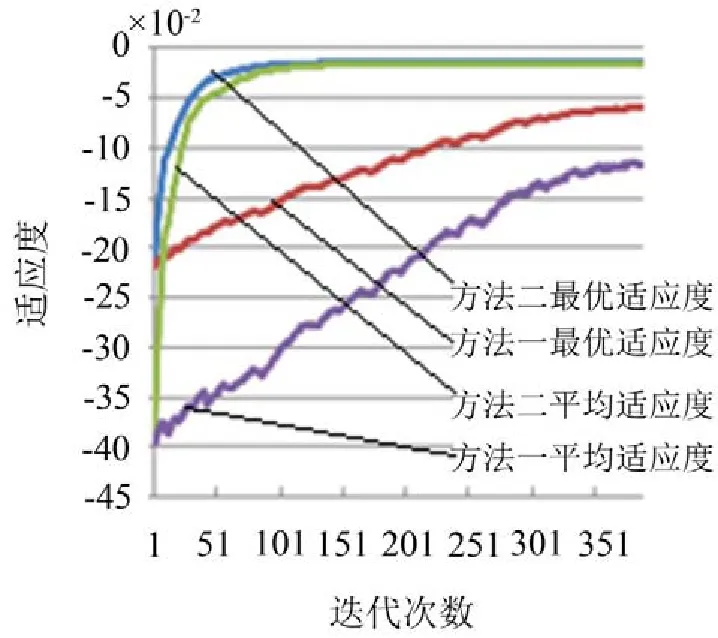
图3　繁殖过程的适应度变化图

3.3 CGHMM训练实验

为了验证方法的有效性，训练实验与后面的诊断实验都包括两种方法，即本文方法和经典方法，分别使用GA和k-means算法初始化CGHMM参数进行模型训练。CGHMM模型的初始化值直接影响到CGHMM训练模型的好坏，训练时不同迭代阶段的输出概率变化能直观显示出模型的优化过程。以正常音训练过程的前50次迭代为例，每一次迭代之后的输出概率如图4所示。

在图4中，本文方法的起步概率较大，是因为使用了GA初始化CGHMM参数的缘故，正因为如此，收敛速度非常快，只需要迭代10次就达到收敛条件，而经典方法迭代了28次才收敛，最终的收敛概率本文方法也高于经典方法，表明本文方法训练过程的速度和效果都要优于经典方法。

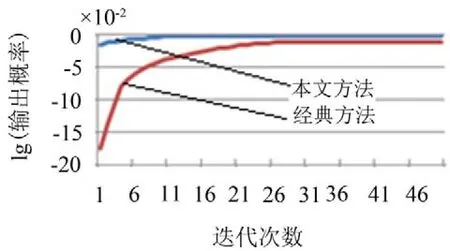
图4　训练迭代过程的输出概率

3.4 CGHMM诊断阶段输出概率实验

多个模型训练好了之后，便可以进入诊断阶段。训练过程中的输出概率能够说明模型好与坏的变化方向，但并不能表明其诊断效果也是相同的变化。为了更进一步测试故障诊断方法的诊断效果，本小节对故障诊断过程中各种故障类型数据在所有模型下的输出概率进行了比较。以30个测试用正常音数据为例，分别使用本文方法和经典方法，在所有故障类型模型下的平均输出概率（因为输出概率太小，取其对数作为纵坐标值）如图5所示，图中未画的部分代表输出概率为零。

图5　诊断阶段正常音的平均输出概率

总的来说，正常音模型下的输出概率都是最高，两种方法的诊断效果都好。不过，为了比较本文方法与经典方法诊断效果好的程度与深度，着重于从下面三个方面分析：

（1）正常音模型下的输出概率，本文方法高于经典方法；

（2）滚动体异音和保持架异音两个模型下的输出概率，本文方法低于经典方法；

（3）正常音模型与其它模型下的输出概率差距，本文方法大于经典方法。

本文方法在三个方面都优于经典方法，并且本文方法在正常音模型与其它模型下的输出概率差距较大，从诊断过程表明，将GA引入到CGHMM模型训练确实是一种可行方法。

3.5 CGHMM诊断精度实验

最终故障诊断精度直接决定着故障诊断方法的好坏，分别使用本文方法和经典方法，以最大输出概率为匹配结果，对正常音、内圈异音、外圈异音、滚动体异音、保持架异音等五类故障状态30个测试用数据所获得的诊断精度如图6所示。

图6　诊断精度

本文方法每一类测试用数据的诊断精度都达到100 %，所有数据测试全部正确，总的诊断精度也是100 %。经典方法对150个数据测试共有6个误识，总的诊断精度为96 %，可以得出，本文方法优于经典方法。

4　结语

基于GA和HMM建模的基本理论，提出了一种故障诊断新方法：CGHMM训练阶段使用GA初始化CGHMM参数。在介绍了该方法总体框架和重要步骤之后，从GA初始化CGHMM、CGHMM训练过程、CGHMM诊断阶段输出概率、CGHMM诊断精度等四个方面详细描述实验仿真的过程与结果，并将本文方法与其它方法进行了比较分析，得出了本文方法效果较好的结论。

参考文献：

[1]艾延廷，冯研研，周海仑.小波变换和EEMD-马氏距离的轴承故障诊断[J].噪声与振动控制，2015，35(1)：235-239.

[2] GAO Hui- zhong, Liang Lin, CHEN Xiaog- uang, et al. Feature extraction and recognition for rolling element bearing fault utilizing short- time fourier transform and non-negative matrix factorization[J]. Chinese Journal of Mechanical Engineering, 2015, 1:96-105.

[3]梁双印，潘作为，祖勇海，等.短时有效值包络分析在风机轴承故障诊断中的应用[J].噪声与振动控制，2015，35 (4)：48-51.

[4] Cody Hudson, Bernard Chen, Dongsheng Che. Hierarchically clustered HMM for protein sequence motif extraction with variable length[J]. Tsinghua Science and Technology, 2014, 6:635-647.

[5]章登义，欧阳黜霏，吴文李.针对时间序列多步预测的聚类隐马尔科夫模型[J].电子学报，2014，12：2359-2364.

[6] Sunil Nilkanth Pawar, Rajankumar Sadashivrao Bichkar. Genetic algorithm with variable length chromosomes for network intrusion detection[J]. International Journal of Automation and Computing, 2015, 3:337-342.

[7]陆汝华，段盛，杨胜跃，等.基于CGHMM的轴承故障音频信号诊断方法[J].计算机工程与应用，2009，45(11)：223-225+234.

[8] Kong Haipeng, Li Ni, Shen Yuzhong. Adaptive double chain quantum genetic algorithm for constrained optimization problems[J]. Chinese Journal of Aeronautics, 2015, 1:214-228.

[9] Morteza Vadood, Majid Safar Johari, Ali Reza Rahai. Relationship between fatigue life of asphalt concrete and polypropylene/polyester fibers using artificial neural network and genetic algorithm[J]. Journal of Central South University, 2015, 5:1937-1946.

Fault Diagnosis Method of Bearings Based on CGHMM Initialization by Genetic Algorithm

LU Ru-hua , YAN Wen-yan
( School of Softwareand Communication Engineering, Xiangnan University Chenzhou 423000, Hunan China)

Abstract:Thecontinuous Gaussian mixturehidden Markov model (CGHMM) hasbeen widely and successfully used in fault diagnosis. However, the traditional CGHMM has some inherent disadvantages, such as the model complexity, the local optimization, low iterativeconvergencespeed and modeling effect dueto initialization of CGHMM parameters. In this paper, the CGHMM model parameters initialized by genetic algorithm were used as the reasonable initial values for CGHMM training. Using this method, the convergence speed can be accelerated and a better effect of modeling can be obtained. Through the simulation experiments in three aspects of CGHMM initialized by genetic algorithm, the CGHMM training process and the CGHMM diagnosis process, it was verified that this method have the advantages of fast training speed and better CGHMM model. The CGHMM diagnosis result demonstrates that the diagnosis precision can achieve 100 %, which ishigher than that of 96 % of theclassical method. Thisresult showsthat thegenetic algorithm can beapplied to CGHMM parameter initialization, andtheproposedmethodisafeasiblemethodfor fault diagnosis.

Key words:vibration and wave; genetic algorithm; initialization; continuous Gaussian mixture hidden Markov model (CGHMM); fault diagnosis

通讯作者：颜文燕（1986-），女，湖南人，硕士，主要研究方向为光通信技术、智能信息处理。E-mail:yanwenyan333@163.com

作者简介：陆汝华（1980-），女，湖南人，硕士，主要研究方向为模式识别、智能信息处理。

基金项目：国家自然科学基金青年资助项目（61402540）；湖南省教育厅资助科研项目（13C879）；湘南学院[2012]125号NO2计算机应用技术创新训练中心项目；湘南学院“十二五”重点学科计算机应用技术学科资助项目。

收稿日期：2015-09-14

文章编号：1006-1355(2016)02-0180-05

中图分类号：TP206+.3

文献标识码：ADOI编码：10.3969/j.issn.1006-1335.2016.02.040