扇扫雷达多目标航迹跟踪算法研究
桂林长海发展有限责任公司 于文才
扇扫雷达多目标航迹跟踪算法研究
桂林长海发展有限责任公司 于文才
【摘要】针对扇扫雷达多目标跟踪时,目标易丢失,精确度低等问题,提出基于传统航迹跟踪技术的改进算法。该算法在数据关联方面采用优化版的ONNCJPDA,并针对雷达扇扫的特征,实时修正两目标点的航迹预测时间,进而修正此种情况下卡尔曼滤波的滤波和外推方程,从而获得正确的目标航迹。
【关键词】多目标;航迹跟踪;ONNCJPDA;航迹动态预测
0 引言
随着信息技术的发展,人们对雷达系统的要求越来越高,原始雷达回波经过点聚处理后在屏幕上显现点迹,已不能满足现在的需求,而是需要显示目标航迹的要求。所谓航迹,指的是对多个目标的若干点迹,进行处理后将同一目标点迹连成的曲线。通过目标跟踪所得到的航迹,与仅有孤立的点信息相比,更加容易获取到目标速度、方向、运动轨迹等目标参数。
1 算法设计原理
航迹跟踪算法设计过程中首先进行确认航迹的数据关联再进行试验航迹的数据关联;随后是航迹跟新和预测,采用卡尔曼滤波对航迹进行更新,并根据目标航迹信息特征对下一时刻的状态信息进行预测;最后是自由点相关,包括了新航迹的建立和自由点的录取。整个航迹跟踪算法设计原理图如图1所示。

图1 航迹跟踪算法设计原理图
2 算法关键技术
航迹跟踪算法包括目标与测量模型、航迹的起始、数据关联、航迹更新与预测和航迹管理。
2.1目标运动模型
本系统针对的目标为地面目标,其特点为机动性较小,可近似为匀速直线运动运动模型。所以跟踪算法运动模型采用CV模型。
针对扇扫雷达扇扫周期之间的差值偏大问题,分析同目标相邻点间的规律,推测目标出现的时刻与扇扫方向、扇扫速度及位置之间的关系,动态的计算获得航迹预测时间,修正不同目标对应的当前状态转移方程,提高跟踪精度。天线扫描模型如图2所示。

图2 雷达天线扫描示意图
若当前天线扫描方向为顺时针,则天线再次扫描到目标A的轨迹如图2中①所示,则航迹预测时间:

若当前天线扫描方向为逆时针,则天线再次扫描到目标A的轨迹如图2中②所示,则航迹预测时间:
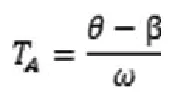
2.2目标量测模型
实际雷达天线连续扫描得到的是极坐标系下的目标的位置信息,即目标距离和方位信息,且所得到的量测值对应雷达固有的量测误差。而目标运动模型是在笛卡尔坐标系下,所以首先应该进行目标量测信息和相应量测误差协方差矩阵的转换。直角坐标系下,目标的状态向量前两帧由目标回波量测向量转换得到:

根据状态转移方程由前一帧的状态向量得到下一帧的状态向量。直角坐标系下回波的测量模型可以用测量方程表示,其中z(k)是目标量测,H为观测矩阵,v(k)为零均值的高斯观测噪声,其协方差矩阵用R表示:

2.3航迹的起始
航迹的起始是指目标点连成曲线航迹的过程。本文采用优化直接法(Rule-Based),最大速度vmax、最小速度vmin,最大加速度amax(amax>0)及最大偏移角度等参数要预先估测,再通过下面的公式判断试验航迹:
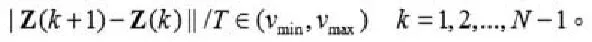
2.4数据关联
数据关联是将相关的数据进行关联,确保航迹正确规划,当新一帧的量测到来时,则要进行数据关联,过程如图3所示。

图3 数据关联过程图
数据关联中提出优化最近邻域简化联合概率数据关联算法(Optimize Nearest Neighbor Cheap Joint Probabilistic Data Association,ONNCJPDA)是在NN、PDA、JPDA、CJPDA之后出现的,如图4所示。
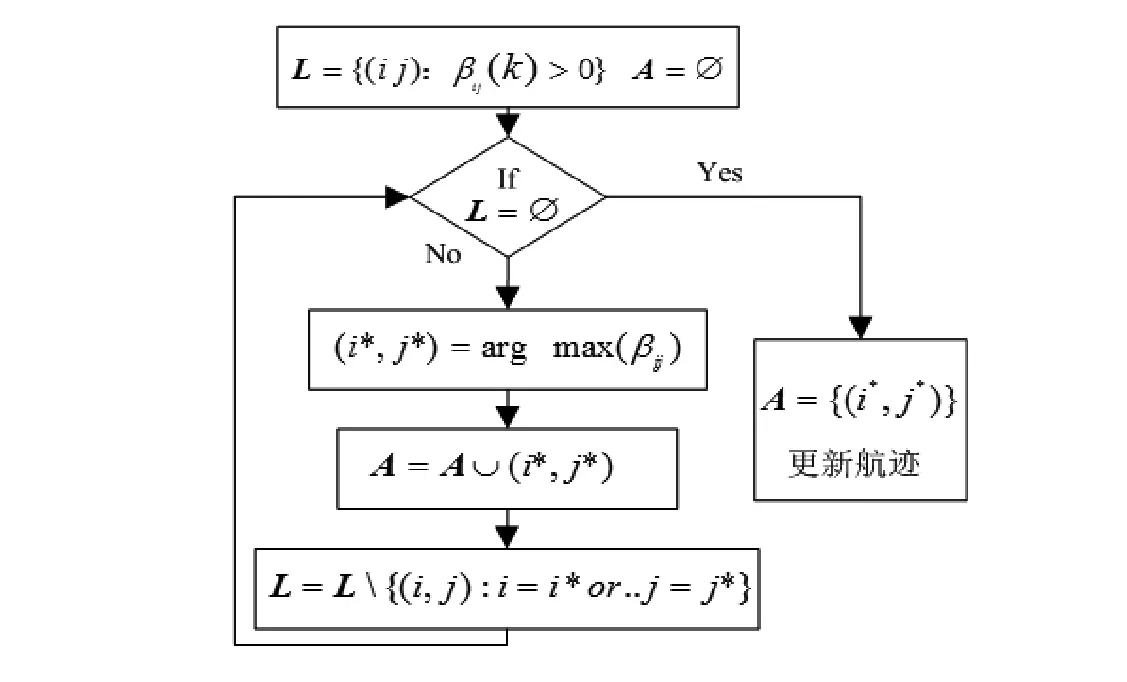
图4 ONNCJPDA处理过程
2.5航迹预测与更新
Kalman滤波中预测与更新,步骤如下:
第1步:预测状态与残差:

第2步:预测误差自相关矩阵和计算新息(残差)的自相关矩阵:
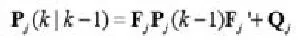

第3步:滤波器增益的计算:

第4步:更新状态和误差自相关矩阵:

2.6航迹确认方法
航迹确认方法是通过相应的准则,判断 试验航迹是否为目标航迹,步骤如下:
第3步:继续N帧重复第2步。
2.7航迹删除方法
为了使虚假航迹减少,通常需要进行航迹终止,其过程通过相应方法对确认航迹判决处理,当确认航迹满足该条件时,则断定是虚假航迹,给以终止,否则维持,其步骤如下:
第2步:重复第1步,直到l=L,则认为该确认航迹为虚假航迹给以终止,否则维持。
当l 本文针对项目所使用的扇扫雷达以及其用途,提出的利于工程实现的改进目标跟踪算法,利用MATLAB仿真,从仿真结果分析,该算法能够有效的实现多目标的实时跟踪,并且达到项目在跟踪模式、目标容量、跟踪精度等各方面的指标要求。但仿真和工程实用有一定的差别,可以在实用时根据跟踪场景、跟踪需求等对例如速度门、波门、M/N准则、L逻辑等一些参数进行相应调整,以达最优效果。 参考文献 [1]张明友,汪学刚.雷达系统[M].电子工业出版社,2006. [2]王国涛,王东进,陈卫东.基于距离和信息的单目标精度跟踪[J].中国科学技术大学学报,2015,35(2). [3]高勤,李志强,都学新.一种新型自适应卡尔曼滤波算法[J].现代雷达,2001(6). [4]戴勇,罗耀华.一种激光雷达的目标跟踪算法[J].电子科技大学学报,第25卷(增刊2). [5]胡峰,孙国基.Kalman滤波的抗野值修正[J].自动化学报,第25卷(第5期). [6]胡晓冬,董辰辉.MATLAB从入门到精通[M].人民邮电出版社,2010,6.3 结论

