基于和差单脉冲天线的多目标分辨算法
吴湘霖+吕晖


摘要: 基于和差脉冲多普勒雷达分辨波束内多目标的应用需求, 建立了天线的阵列流形矩阵数学模型, 提出了一种有效的和差MUSIC算法。 该算法能够在目标角度、 多普勒频率间隔均小于系统分辨率的条件下, 有效完成对多目标的分辨与测量任务。 数字仿真实验验证了新算法的有效性。
关键词: 脉冲多普勒雷达; 和差单脉冲天线; 多目标; MUSIC算法
中图分类号: TN959.1+7 文献标识码: A文章编号: 1673-5048(2016)05-0039-06
Abstract: Based on the requirements of ∑Δ monopulse doppler radar resolving multitargets, an array manifold matrix model is established, and an efficient ∑Δ MUSIC algorithm is presented. This algorithm can resolve and measure multitargets in the condition that the target angle and doppler frequency interval are less than the system resolution. Simulation results verify the algorithm effectiveness.
Key words: pulse doppler radar; ∑Δ monopulse antenna; multitarget; MUSIC algorithm
0引言
脉冲多普勒(PD)体制、 和差单脉冲测角目前在机载[1]与弹载雷达领域广泛使用, 但对目标参数的测量分辨性能存在一定的限制。 和差比幅、 比相等单脉冲测角的角度分辨率为所使用天线的波束宽度, 该宽度由天线阵面孔径的电尺寸决定; 而采用脉冲多普勒工作体制的雷达导引头多普勒分辨率由相参积累周期的倒数决定, 同时受到抗频域泄露所需窗函数对回波信号谱线的展宽, 以及分辨算法本身的损失影响, 通常为数百至数千赫兹。
对于比较理想的单目标环境, 脉冲多普勒体制、 和差单脉冲测角的目标分辨与参数测量能力已经足以满足需求。 但在实际作战环境中, 往往面临如群目标攻击、 拖曳或伴飞诱饵干扰等多目标分辨的需求, 此类多个目标(或真假目标)之间的角度与多普勒频率差异经常小于雷达的波束与多普勒分辨单元, 使用现有脉冲多普勒体制、 和差单脉冲测角方法通常难以有效分辨[2-3], 多目标回波(或回波与干扰)相互干涉混叠, 测量输出的目标信息往往位于群目标的矢量中心。 对于机载雷达而言, 这一现象就代表着对目标威胁特性与对机载武器指示的误差, 对弹载雷达而言则代表着攻击方向偏差, 导致脱靶。
波束/多普勒分辨单元内的多目标检测与测量问题, 已有较多文献进行研究。 双基SAR、 前视SAR技术理论上可以有效提高机载、 弹载雷达前视探测的角度分辨率, 但需要通过构造复杂几何观测模型或者大天线阵列, 代价昂贵; 文献[4-6]分别通过瞬时匹配矩方法、 模型简化似然求解方法以及计算质心角度与加窗聚类相结合的方法, 各自获得了多目标高分辨角度估计, 但这几类方法或必须已知各目标的信号功率、 或已知二者的相对功率比、 或仅适用于两个完全对等目标, 对于实际应用难以保证。
基于特征子空间的高分辨率算法, 如MUSIC[7-8]等是有效的解决途径。 此类算法通常要求使用多通道相控阵天线, 且要求多目标之间具有非相干特性, 如何改造此类算法, 在现有和差单脉冲测角与脉冲多普勒体制基础上, 实现对角度、 多普勒频率差异小于常规分辨率的多目标分辨与测量, 是本文需解决的主要问题。
1和差单脉冲测角
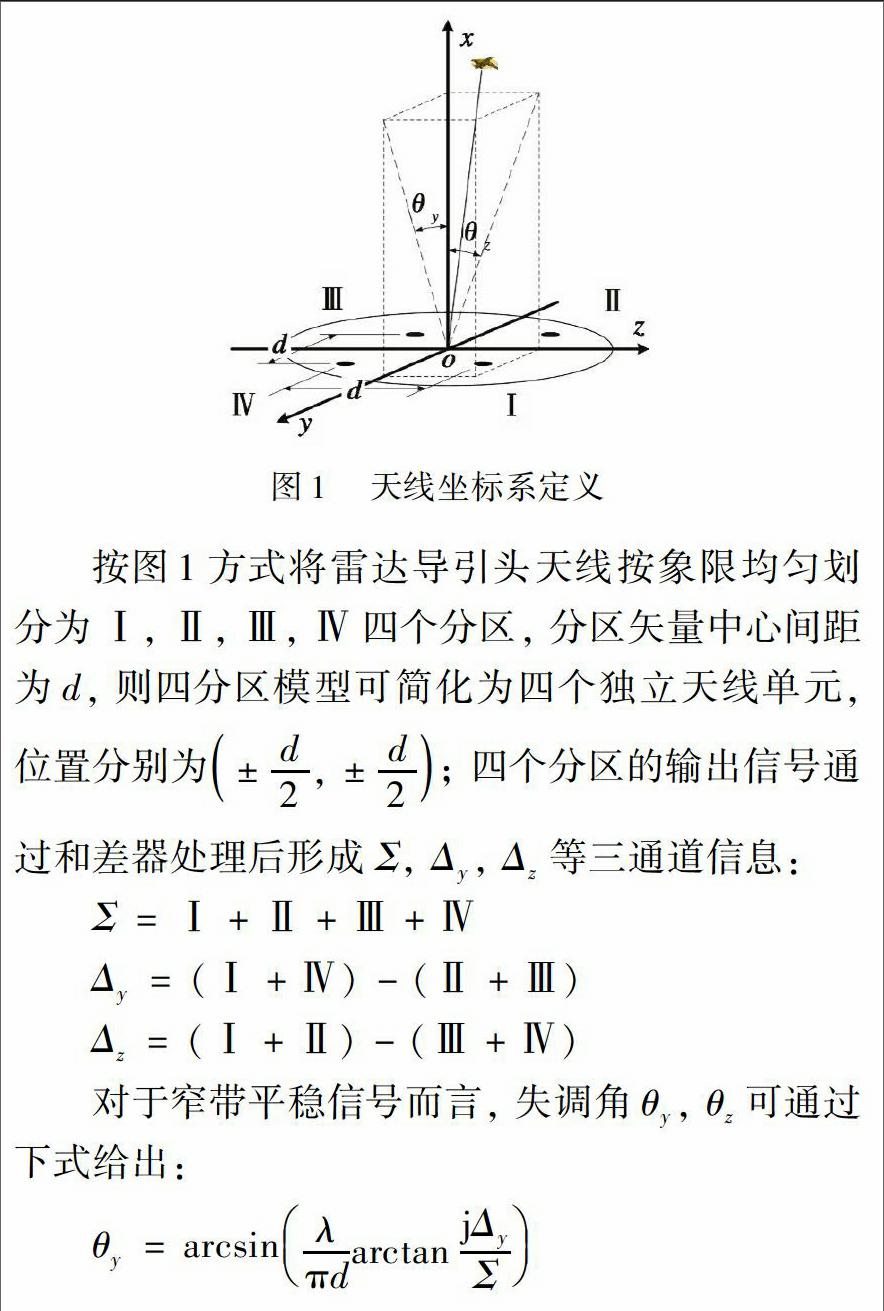
定义坐标系如图1所示。 其中坐标系原点定义为天线阵面中心; x轴定义为天线法线方向; y, z轴在天线阵面上正交建立。 目标空间位置信息通过失调角θy和θz确定, 失调角θy和θz分别定义为目标与坐标系原点连线在xoy, xoz平面上的投影与x轴之间的夹角。
2和差MUSIC
2.1MUSIC算法原理
多信号分类算法(MUSIC)最初由Schmit在1981年提出, 属于特征结构类高分辨率阵列处理技术。 该方法通过协方差矩阵的特征分解, 构造与阵列流形空间相一致的信号子空间, 以及与之正交的噪声子空间, 并利用子空间正交性构造空间伪谱, 以实现对相关参数的渐进无偏估计。
2.2和差MUSIC算法
如前所述, 常规MUSIC算法存在的问题主要在于: 该算法是针对阵列天线系统设计, 输出信号模型对于导向矢量/流形矩阵的定义根据独立单元天线阵列建立, 未考虑最常使用的和差单脉冲天线模型; 另外, 上述定理成立的一个重要前提条件是多个回波信号之间不相关, 但实际应用中多目标之间的频率差异往往小于系统分辨率, 这使得多个目标的回波信号之间具有较强的相关性, 直接使用常规MUSIC算法会导致信号子空间非正常降维, 相关目标的MUSIC伪谱发生谱峰融合, 算法失效。
该虚拟天线由物理天线的K个延时输出在空间域上扩展得到, 实质就是域输出信号的对时平滑处理。
和差MUSIC算法时域平滑阶数K的选取取决于多目标之间的角度、 多普勒频率以及幅度差异。 角度、 多普勒频率差异越小、 幅度差异越大时, K值应适当取大。 时域平滑阶数K设定过小将导致无法正常分辨多目标, 但设定过大时会导致计算量增加。
按常规MUSIC算法原理, 对虚拟天线输出z(t)构造协方差矩阵, 并通过特征分解构造噪声子空间, 使用如上虚拟天线导向矢量(θy, θz, fd)对定义域范围内的失调角θy和θz, 以及多普勒频率fd进行搜索, 即可通过三维谱峰获得对目标与诱饵的参数估计。
3数字仿真
3.1常规算法仿真
考虑一个典型的X波段弹载应用环境:
(1) 工作频段X波段λ=0.025 m;
(2) 天线分区间距d=0.07 m;
(3) 相参积累周期T=2 ms;
(4) FFT积累使用Hamming窗加权。
在此条件下天线波束宽度大约为±5°, 多普勒分辨率为714 Hz。 设置典型双目标, 如表1所示。
3.2MUSIC单次仿真分析
使用相同的X波段弹载雷达设置, 对如表2所示的典型三目标场景进行单次的和差MUSIC仿真, 其中时域平滑阶数K取8。
受多目标相关性影响, 在为搜索矢量(θy,θz, fd)设置不同的多普勒频率试探值fd后, (θy,θz)二维谱均会出现局部峰值, 但(θy, θz, fd)三维全局峰值仅在预设各个目标位置出现。 因此三维谱全局搜索可以正常发现真实目标, 全局峰值对应的(θy, θz, fd)设置值即为三目标的参数测量值, 如表3所示。
3.3蒙特卡罗仿真分析
为验证和差MUSIC算法的有效性, 采用同样仿真条件, 对3.1节所示双目标场景, 重复100次蒙特卡罗仿真实验。
对和差MUSIC算法输出的双目标三维参数测量信息进行统计, 结果如图4所示。 其中图4(a)给图4和差MUSIC算法参数分布
出了100次仿真的θy, θz测量散布情况, 图4(b)给出了这些仿真中局域峰值随多普勒频率的变化情况。 可以看出, 仿真算法有效, 通过三维谱的全局搜索可以有效分辨双目标。 给出的参数测量均值如表4所示, 进一步显示和差MUSIC算法有效完成了对双目标的分辨任务, 双目标参数测量值与真实值差异很小, 满足系统需求。
4结论
针对现有机载、 弹载单脉冲PD雷达对抗群目标、 拖曳或伴飞诱饵干扰等多目标分辨的需求, 在现有和差单脉冲天线与接收系统的基础上建立了对应的阵列流形矩阵数学模型, 提出了一种有效的和差MUSIC算法。 数字仿真结果显示: 和差MUSIC算法能够在目标角度、 多普勒频率间隔均小于系统分辨率的条件下, 有效完成对多目标的分辨与测量任务。
参考文献:
[1] 贲德, 韦传安, 林幼权. 机载雷达手册技术[M].北京: 电子工业出版社, 2006.
[2] Zhang X, Willett P K, BarShalom Y. Monopulse Radar Detection and Localization of Multiple Unresolved Targets via Joint Bin Processing[J].IEEE Transactions on Signal Processing, 2005, 53(4): 1225-1236.
[3] Sherman S M. Complex Indicated Angles Applied to Unresolved Radar Targets and Multipath [J]. IEEE Transactions on Aerospace and Electronic Systems, 1971, 7(1): 160-170.
[4] Blair W D, BrandtPearce M. Monopulse DOA Estimation of Two Unresolved Rayleigh Targets [J]. IEEE Transactions on Aerospace and Electronic Systems, 2001, 37(2): 452-469.
[5] Wang Z, Sinha A, Willett P, et al. Angle Estimation for Two Unresolved Target with Monopulse Radar [J]. IEEE Transactions on Aerospace and Electronic Systems, 2004, 40(3): 998-1019.
[6] Zhou Lanfeng, Zhang Min, Zhao Yinan. Angle Estimation of Two Unresolved Swerling I Targets in Monopulse Radar[C]∥International Conference on Microwave and Millimeter Wave Technology, Chengdu, 2010: 1622-1625.
[7] Schmit R O. A Signal Subspace Approach to Multiple Emitter Location and Spectral Estimation[D]. Palo Alto: Stanford University, 1981.
[8] Farrier D R, Jeffries D J, Mardani R. Theoretical Performance Prediction of the MUSIC Algorithm[J].Communications, Radar and Signal Processing, IEE Proceedings F, 1988, 135(3): 216-222.
[9] 刘德树, 罗景青, 张剑云. 空间谱估计及其应用[M]. 合肥: 中国科学技术大学出版社, 1997.
[10] Lemma A N, Van der Veen A-J, Deprettere E F. Analysis of Joint AngleFrequency Estimation Using ESPRIT[J]. IEEE Transactions on Signal Processing, 2003, 51(5): 1264-1283.

