基于Q学习的多目标分时段路口交通控制
张辰
摘 摘要:针对路口堵塞,提出了一种基于Q学习算法的多目标分时段路口信号灯控制方法。该方法在多个单路口交通性能评价指标的基础上,考虑了不同时段所具有的不同流量特征,从而设计了一套混合型的综合信号灯控制策略。最后在VISSIM上对本策略进行了仿真实验,验证了有效性。
关键词: Q学习;多目标;分时段;交通控制
中图分类号:TP393.08 文献标识码:A 文章编号:1009-3044(2016)03-0291-02
1 引言
当今,汽车已经成为人们出行的主要手段。然而,汽车的普及与城市路口建设的局限性,使得如何有效地管理交通成为了一个非常重要的课题。为了做好路口的交通控制问题,国内外许多专家都对此进行了大量的研究,近年来,交通控制理论越来越成熟。在路口控制问题上,提出了很多不同的性能评价指标,并且从这些基本指标出发,逐渐从对单一目标的优化发展到对多目标的优化。但是后者存在一个问题,就是多目标之间可能会有冲突,从而无法左右兼顾,达到最理想的情况。为了解决这个问题,研究人员采用了诸如遗传算法,模糊偏好,粒子群等多种算法,并由此产生了一套日趋完善的多目标优化理论。同时,交通控制方法已经从传统的理论发展到与人工智能,神经网络,自学习等结合起来应用,并且产生了大量实际有效的成果[1]。其中,强化学习算法(Reinforcement Learning, RL)被认为是一种利用自学习来解决交通控制的非常有效的方法。而Q学习[2]则是强化算法中非常具有代表性的一种算法,对于其在路口交通控制中的应用也已经有了一定的研究历史。
本文在国内外已经取得成果的基础上[3],结合Q学习算法,提出了一种多目标,多时段的混合控制策略。该策略考虑了不同交通状况和时段下,人们所着重的优化目标也会不同,因此需要根据实际情况,自动权衡,修正各目标之间的权重关系。接着利用Q学习算法,将混合策略应用到信号灯的控制上,使得控制具有自适应的特点。最后与传统的策略[4][5]进行比较,证明了本混合策略的显著的优化效果。
2 基于Q学习的控制策略
本文提出的方法是一种多目标,多时段的混合控制策略。本策略由主要有两个方面:多目标,多时段。
对于多目标来说,本文具体分析了各个路口性能评价指标的意义,并选取了几个具有较好代表性的指标来作为优化目标。在策略中,我们采取线性组合的方式,将几个目标组合在一起。每一个目标之间通过权重来确定其对整个优化函数所做的贡献,从而达到最优化的操作。
对于多时段来说,在交通控制中,评价指标如何选取与当前交通流的具体情况有着密切的联系。随着路口交通堵塞情况的变化,优化目标之间的权重也应该有所改变。
2.1 参数设计
本策略采用了如下多目标参数:
通行能力(Capacity)
通行能力是指在其余条件不变的情况下,在单位时间内,通过交叉口的最大车辆数。通行能力在一定程度上可以反映交通情况是否畅通,以及畅通的程度。
延误时间(delay time)
延误时间是指,当一辆车从进入交叉口道路一直到离开,由于交叉口不畅通所导致的额外的行驶时间。延误时间一般由停车时间和因为拥堵而导致的缓慢行驶所浪费的时间组成。
饱和度(saturation degree):
饱和度是指,路口中入口方向的到达车流与通行能力的比值。
2.2 Q学习参数设计State
在单交叉口中,由一个Agent负责感知和接收当前路口的环境参数值。在本算法中,我们考虑了以下几个常用参数:
1. 当前相位的编号。
2. 当前相位中,红灯方向的排队长度和。
3. 当前相位中,绿灯方向的车流数量和。
Action
采用(保持/切换)的两种行为组成的集合。相对前者来说,后者不仅简单,适合可变周期,其只有两个值的优点更使得在与state进行结合配对时,状态空间呈指数级的减小,从而在一定程度上加快了Agent的响应速度。
Reward
定义回报函数为两个相邻时段的交通性能值的差。
3 实验结果分析
实验在VISSIM上仿真了一个主要交通路口。路口信息为:4方向,每个方向3条车道(进车道,直行/右转出车道,左转出车道)
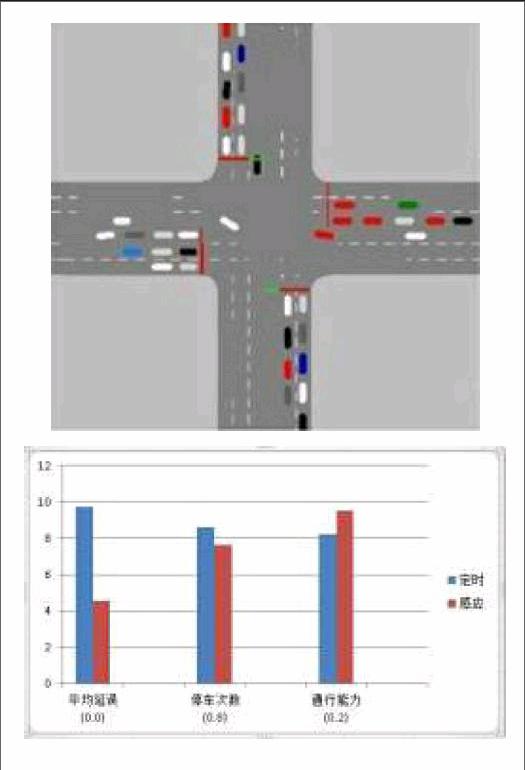
这是中度拥堵的情况下,自适应策略的相对百分比评价指数提升。在中度拥堵的情况下,三个指标的提升相对来说比较平均,基本都围绕8%的水平。在中度拥堵的情况下,策略对平均停车次数具有强烈的偏好性(0.8),对通行能力具有次级偏好(0.2),因此,策略在执行过程中以这两个为目标进行优化。相对于重度和轻度两种情况来说,停车次数指标在中度拥堵情况中得到了最好的提升,而通行能力的提升水平也是比较高的。
4 结论
本文提出了一种分时段,多目标混合交通控制策略,设计将分时段与多目标进行结合,并应用到路口控制中,可以最大限度,最广面积的考虑到路口的复杂的需求。通过Q学习实现了该策略,展示了以Q学习为代表的RL算法在交通路口控制中的可行性和所具有的优势。使用Q学习算法,路口的性能评价得到了显著有效地提升。结果显示了Q学习在复杂多变的路口交通情况中,与传统的通过建立固定模型进行控制的方法,具有更大的灵活性和自适应性。
参考文献:
[1] 卢凯.交通信号协调控制基础理论与关键技术研究[D].华南理工大学,2010:46-48.
[2] Watkins P Dayan. Q-learning. Machine Learning, 1992, 8(3): 279-292 .
[3] 徐建闽.交通管理与控制[M]. 北京:人民交通出版社,2007:139-140.
[4] Waltz M D,Fu K S. A Heuristic Approach to Reinforcement Learning Control System[J].IEEE Transaction on Automatic Control, 1965, 10(4):390-398.
[5] Siagh S P. Reinforcement Learning with Replacing Eligibility Traces[J].Machine Learning, 1996, 22: 159-195.

