加权分数傅里叶变换在混合系统中的应用

陈　青， 孙海信， 齐　洁， 顾亚平， 王华奎

(1. 水声通信与海洋信息技术教育部重点实验室(厦门大学)， 361005 福建 厦门；2. 中国科学院声学研究所， 100190 北京； 3. 水声对抗重点实验室(91388部队)， 524022 广东 湛江)



加权分数傅里叶变换在混合系统中的应用

陈青1， 孙海信1， 齐洁1， 顾亚平2， 王华奎3

(1. 水声通信与海洋信息技术教育部重点实验室(厦门大学)， 361005 福建 厦门；2. 中国科学院声学研究所， 100190 北京； 3. 水声对抗重点实验室(91388部队)， 524022 广东 湛江)

摘要:为提高通信系统在复杂水声环境下的鲁棒性，提出基于加权分数傅里叶变换WFRFT(weighted fractional Fourier transform)的混合载波系统. 对混合系统进行优化设计，以最低误比特率为优化目标，求解得到系统的最优变换阶次，得到优化的系统性能. 仿真和水池实验表明，基于WFRFT的混合载波系统在多径信道下的误比特率介于传统的单/多载波系统之间；而在双选信道下，其最优阶的系统性能优于单/多载波系统. 该混合系统具有单/多载波的优良性能，在提高通信系统鲁棒性方面，具有很大的应用前景.

关键词:加权分数傅里叶变换；混合载波系统；水声环境；最优阶

目前，水声通信中主要应用两种机制：多载波正交频分复用OFDM(orthogonal frequency division multiplexing)[1]与单载波频域均衡SC-FDE(single carrier-frequency domain equalization)[2]. OFDM系统主要用于克服多径传输，且频谱利用率高[3]，但存在高峰均比和对频偏敏感等问题[4]；SC-FDE系统能够降低峰均比，对频偏不敏感，但频谱利用率低[5]. 可见，OFDM和SC-FDE各有优缺点.

本文提出一种基于WFRFT的混合载波系统. 它只需一套物理层传输设备就可实现单/多载波系统以及分数域系统，是一种真正意义上的混合载波调制系统[6]. 他可与现有的传输体制相兼容，也可在各分数域系统间平滑过渡，能与实际信道相匹配. WFRFT系统作为一种将单/多载波结合的传输手段尚未受到广泛研究，它在不同传输环境下的最优化传输也未发现相关文献. 本文将在水声信道典型的多径和多普勒环境下，研究基于WFRFT的混合载波通信系统性能，并提出该系统最优阶的选取方法.

1加权类傅里叶变换基本理论

1.1加权分数傅里叶变换[7]的定义

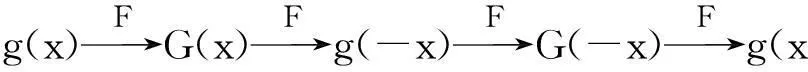
Fα[g(x)]=w0(α)g(x)+w1(α)G(x)+

w2(α)g(-x)+w3(α)G(-x).

(1)

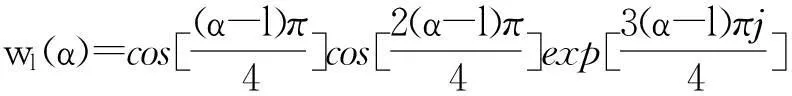
(2)

式中α的周期为4，一般将区间[0,4]定义为α的主周期.

传统傅里叶变换将时域信号由时域轴逆时针旋转π/2到频域轴. 时域信号和频域信号在时频域平面上是正交的.

1.2加权分数傅里叶变换的物理实现

离散序列的反转操作(以g(-m)为例)为

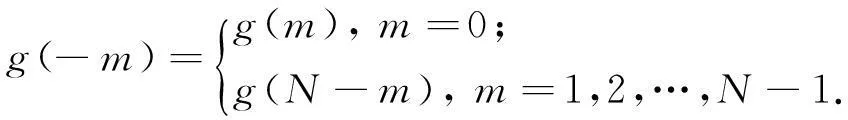
(3)

WFRFT可用FFT实现，从而降低实现的复杂度. 具体实现见图1系统结构[6].

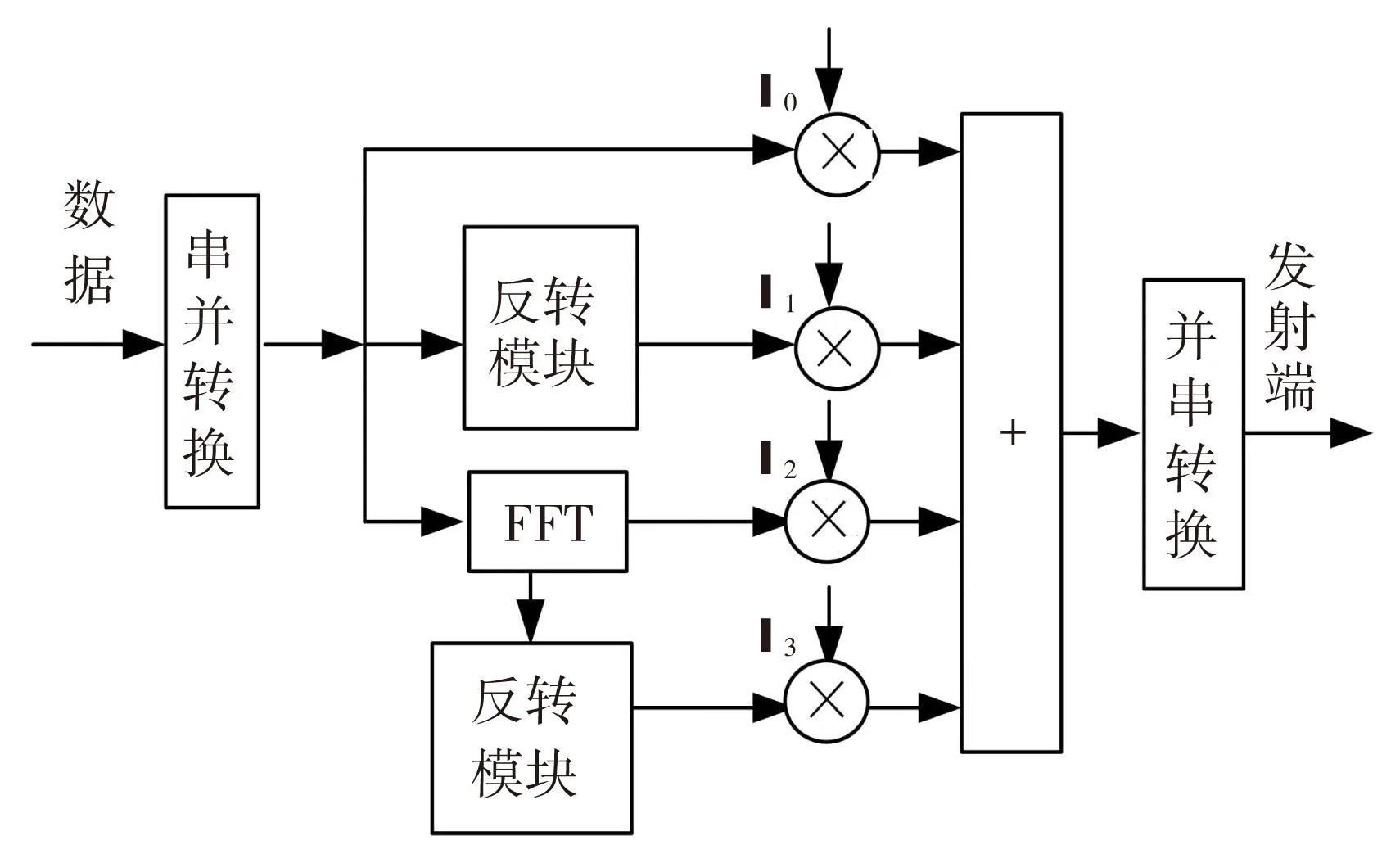
图1　基于FFT的WFRFT系统实现结构

由图1可见，一次WFRFT只需进行一次相同长度的FFT运算，从乘法次数角度，两者的复杂度基本处于同一数量级上. WFRFT只是在加权过程中多了4N次乘法运算. 因此，WFRFT算法在硬件上可实现.

2基于WFRFT的混合载波通信系统

将WFRFT引入通信系统，并利用WFRFT的边界性和可加性构建混合载波系统[9],见图2. WFRFT的边界性即时域信号g(x)的0阶变换结果为信号时域形式，α=1时为信号频域形式；可加性可描述为

(4)

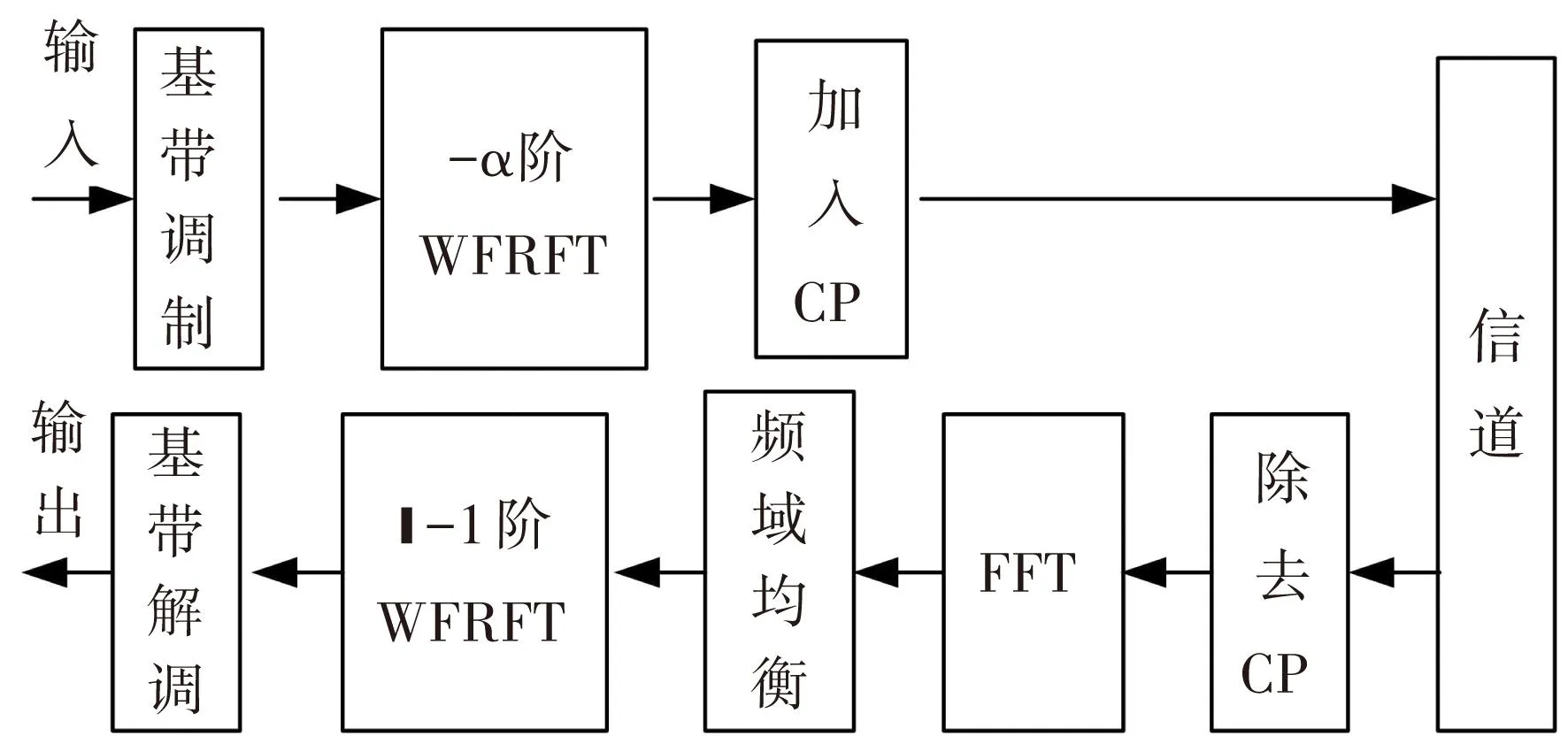
图2　基于WFRFT的混合载波系统框图

输入信号是由α阶分数域变换到时域，接收信号先经过FFT变换到频域进行均衡后，再经过(α-1)的 WFRFT变换回α阶分数域. 混合系统在取特定参数时可转化为现有的单/多载波系统. 当α=0时，混合系统为SC-FDE系统见图3；当α=1时，对应OFDM系统[10]见图4.

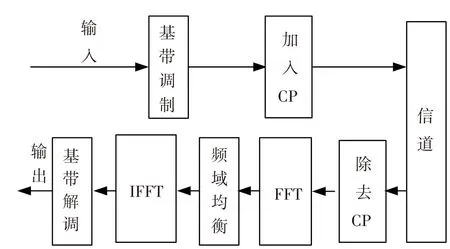
图3　SC-FDE的基本系统框图

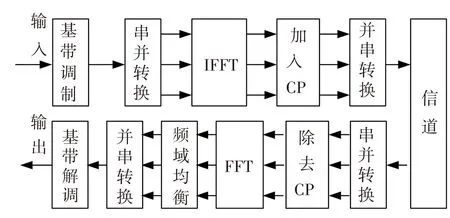
图4　基于FFT的OFDM系统实现框图

3WFRFT系统优化

在不同环境下，通信系统的性能会差别很大，多径和多普勒的影响也会非常明显. 因此在不同环境下，如何设计最优系统和求得系统最优解，对于提升WFRFT系统的性能，具有重要意义.

最佳通信系统是与信道不同传输条件紧密结合的. 一般情况下，通信系统是以误比特率作为系统性能的衡量标准.

(5)

式中:biterr为传输中错误比特数，bitall为传输的总比特数.

考虑到信号传输会受到通信环境中各种干扰的影响，而不同变换阶次下系统受这些干扰影响的程度也不同. 干扰程度越小，对应误比特率也越小. 因此结合变换阶次，设计系统优化目标，实现最优的WFRFT系统设计.

主要考虑多径和多普勒这两个因素，水声信道的冲激响应为

(6)

式中: L,ai,τi,fdi分别为多径数、幅度、时延、多普勒频移.

源信号x(t)经过信道传输后，接收信号y(t)为

(7)

式中：n(t)为高斯白噪声信号,当采样频率为Fs时，接收信号的离散表示形式为

(8)

接收信号y(k)包含了源信号x(k)信息以及多径、多普勒和噪声造成的干扰信息d(k). 可用另一种表达形式:

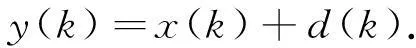
(9)

在通信系统中，接收端接收信号后还要经过解调和判决，d(k)的大小会影响信号最终的正确判决，从而影响系统性能. 而WFRFT系统中，选择不同的变换阶次，信号经过信道所受到的干扰程度也不同. 令x=(x(1),x(2),…),y=(y(1),y(2),…)，则在WFRFT系统中

(10)

Nα越小，即干扰信息对源信号的影响越小，系统误比特率越小，系统性能更好. 因此，以Nα的最小值为优化目标，在α主周期内进行搜索，当Nα最小时对应的α即为最优阶. 最优阶选取问题的解可描述为

(11)

式中：‖·‖2为2-范数，Fα[·]为α阶WFRFT. 算法具体流程见图5.

将最优阶选取算法引入图2所示系统中，得到的系统结构图见图6.

在发送信号s前，先发送一串具有和s相同长度及结构的已知序列x. y为接收信号. 根据图5所示算法，选取最优阶αopt. 将αopt反馈回发送端，再发送s. 此时，基于WFRFT的混合载波系统是在αopt模式下通信的，系统误比特率最低，性能最好.

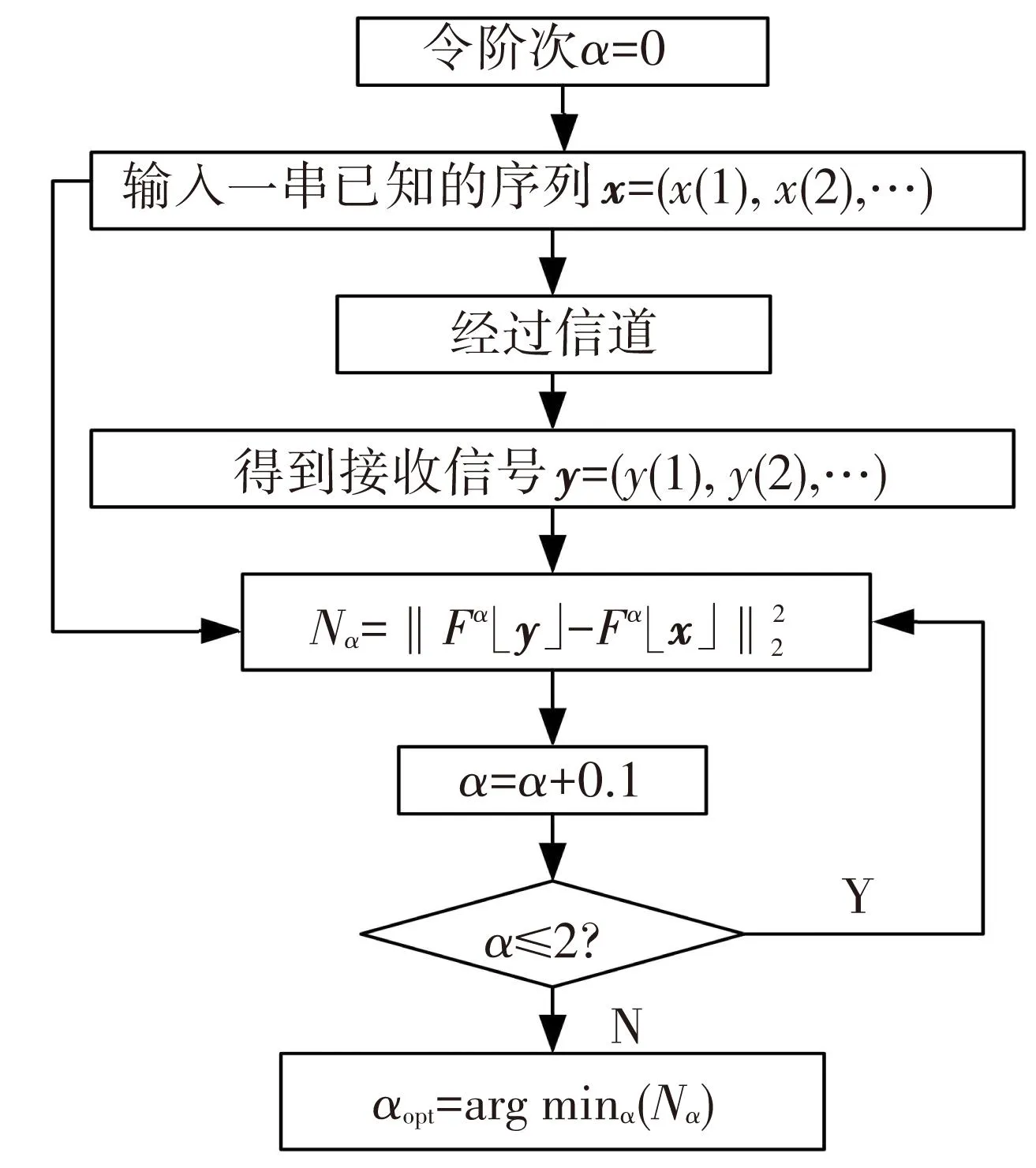
图5　最优阶选取算法流程

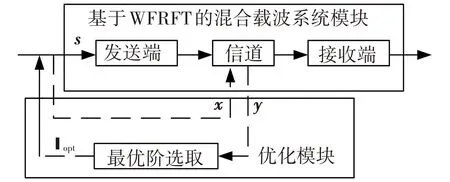
图6　引入最优阶选取算法的WFRFT系统

4仿真和水池实验

4.1仿真

考虑到水声环境多径时延严重，在多径信道下进行了仿真. 当多普勒频移为0 Hz时，根据式(6)，由表1参数建立多径仿真信道. 其中最大多径时延为12 ms，且第二径的信号幅度衰减为源信号的0.82倍，对第一径信号干扰比较大，则该多径信道造成的码间干扰会比较严重. 相关仿真参数见表1、2.

表1　信道的时延和幅度衰减

表2　系统仿真参数

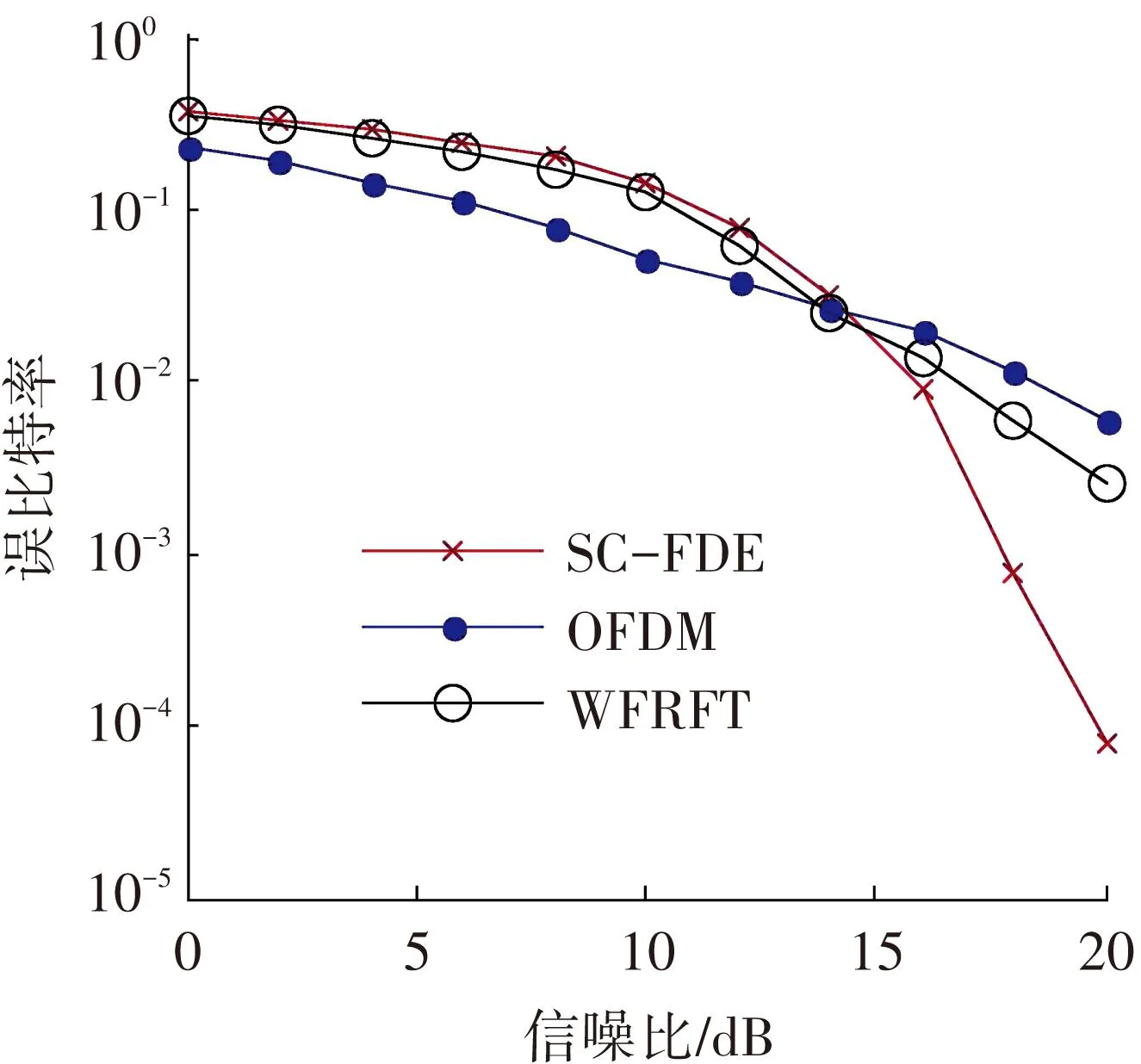
在多径仿真信道下，由式(5)可得SC-FDE系统、OFDM系统和WFRFT系统的误比特率. 3种系统在不同信噪比下的误比特率曲线见图7. 由图7可见，当信噪比<14 dB时，3种系统的性能排序为OFDM14 dB时有SC-FDE

图7　3种系统在不同信噪比下的误比特率(α=0.5)

图8　不同变换阶次下的混合载波系统性能

因为WFRFT系统可兼容单/多载波系统，经过最优阶算法，在低信噪比下系统选取α=1，WFRFT系统转换为OFDM系统，此时系统得到最低误比特率；在高信噪比下系统选取α=0，WFRFT系统转换为SC-FDE系统，此时系统得到最低误比特率. 在多径信道下，基于WFRFT的混合载波系统可依具体情况选择最优阶，从而更好地匹配信道，达到最优性能. 仿真结果见图9. 另外，作为单/多载波混合体制存在的WFRFT系统对时间选择性衰落与频率选择性衰落都存在抵抗性，从而比单独的单/多载波系统拥有更优异的系统性能. 因此，在多径和多普勒信道下进行仿真，最大多普勒频移为200 Hz，具体仿真参数见表1、2. 在该双选信道下，混合系统经过最优化过程，选取α=0.4，此时系统得到最低误比特率. 仿真结果见图10.

图9　3种系统在不同信噪比下的误比特率(α可变)

图10　3种系统在双选信道下的性能比较

由图10可见，信噪比在0～5 dB时，3种系统的误比特率相差不大；信噪比>5 dB时，基于WFRFT的混合载波系统的误比特率很明显低于其它两种系统. 以信噪比为20 dB为例，WFRFT系统比OFDM系统的误比特率降低0.008，比SC-FDE系统降低0.017，显示出WFRFT系统比其它两种系统具有更强的抗衰落能力，有一定实用价值.

综上所述，基于WFRFT的混合载波系统只需一套物理层传输设备，可根据不同信道环境选择合适的α，以更好地匹配信道，比传统的单/多载波系统具有更好的性能.

4.2水池实验

该实验是在厦门大学通信工程系实验水池中完成的. 水池4面铺设瓷砖，声信号在水池中传输时存在严重的多径时延. 实验过程见图11，换能器和水听器相距8 m. 系统参数的设置见表3.

图11　水池实验过程示意

信号映射同步信号数据长度有效带宽/kHz有效速率/(kbit·s-1)采样频率/kHz载波频率/kHzQPSKChirp信号1024636611

换能器和水听器保持静止，此时信道表现为多径时延特性，在信噪比估计值分别为18.801 0、12.658 8 dB时得到第1、2组数据；水听器以20 m/s的速度移动造成约147 Hz的最大多普勒频移，此时信道表现为多径时延和多普勒频移的特性，在该信道下得到第3组数据. 实验数据见表4.

表4　水池实验结果(误比特率)

由表4第1、2组数据可得，WFRFT系统性能介于其它两种系统之间. 在信噪比为18.801 0 dB且α=0时，WFRFT系统与SC-FDE系统性能相近，可得最小误比特率；在信噪比为12.658 8 dB且α=1时，WFRFT系统与OFDM系统性能相近，可得最小误比特率. 由表4第3组数据可得，WFRFT系统有优于其它两种系统的变换阶次，当α=0.4时，WFRFT系统的误比特率最低.

因此，在不同信噪比以及多径、多普勒的信道环境下，WFRFT系统通过选取最优阶可得最优系统性能. 与传统的单/多载波系统相比，WFRFT系统具有更好的性能.

5结语

现有的两种载波系统—单载波系统和多载波系统，各自存在优缺点. 本文提出的WFRFT混合载波系统能体现单/多载波系统混合的特性，通过研究该系统在多径信道和双选信道下的性能，结合信道特点和WFRFT变换性质，以最低误比特率为优化目标，可得系统最优阶，得到在不同传输环境下的最优传输系统. 最后经过实验验证：该混合系统在多径信道下，系统性能处于单/多载波系统之间；在双选信道下，混合系统有优于其它两种系统的变换阶次. 混合系统可根据信道环境选择最优阶，使系统跟信道匹配，保持最优的系统性能，具有一定应用前景.

参考文献

[1] WANG Zhaohui, HUANG Jie, ZHOU Shengli, et al. Iterative receiver processing for OFDM modulated physical-layer network coding in underwater acoustic channels [J]. IEEE Transactions on Communications, 2013, 61(2): 541-553.

[2] 郭瑜晖,孙海信,程恩,等. 水声系统单载波频域均衡方法比较[J]. 厦门大学学报(自然科学版),2012,51(5): 849-853.

[3] 徐小卡,桑恩方,李娜,等. 基于DFT的OFDM水声通信信道估计算法[J]. 数据采集与处理,2009,24(1): 44-48.

[4] 黄新林,王钢,马永奎,等. 一种高效的OFDM比特功率分配算法[J]. 哈尔滨工业大学学报,2010,42(9): 1379-1382.

[5] 王荆宁,沙学军,谭学治. 单载波频域均衡中的协作分集方法[J]. 哈尔滨工业大学学报,2011,43(7): 42-45.

[6] MEI Lin, SHA Xuejun, ZHANG Naitong. The approach to carrier scheme convergence based on 4-weighted fractional Fourier transform [J]. IEEE Communication Letters, 2010, 14(6): 503-505.

[7] MEI Lin, SHA Xuejun, RAN Qinwen, et al. Research on the application of 4-weighted fractional Fourier transform in communication system [J]. Science China (Information Sciences), 2010, 53(6): 1251-1260.

[8] WANG Kun, SHA Xuejun, MEI Lin. On interference suppression in doubly-dispersive channels with hybrid single-multi carrier modulation and an MMSE iterative equalizer [J]. IEEE Wireless Communications Letters, 2012, 1(5): 504-507.

[9] WANG Kun, SHA Xuejun, MEI Lin, et al. Performance analysis of hybrid carrier system with MMSE equalization over doubly-dispersive channels [J]. IEEE Communications Letters, 2012, 16(7): 1048-1051.[10]CVIJETIC N. OFDM for next-generation optical access networks [J]. Journal of Lightwave Technology, 2012, 30(4): 384-398.

(编辑王小唯苗秀芝)

Application of weighted fractional Fourier transform in hybrid system

CHEN Qing1, SUN Haixin1, QI Jie1, GU Yaping2, WANG Huakui3

(1. Key Laboratory of Underwater Acoustic Communication and Marine Information Technology, Ministry of Education, School of Information Science and Engineering, Xiamen University, 361005 Xiamen, Fujian, China;2. Institute of Acoustics, Chinese Academy of Sciences, 100190 Beijing, China;3. Science and Technology on Underwater Acoustic Antagonizing Laboratory, No.91388 Unit of PLA, 524022 Zhanjiang, Guangdong, China)

Abstract:To improve the robustness of the communication system in complex underwater acoustic environment, the hybrid carrier system based on WFRFT was put forward. To obtain the optimal transformation order, the hybrid carrier system is designed with the lowest bit error rate as optimization goal. Simulation results show that BER performance of hybrid carrier system is between the traditional single/multi carrier systems in multipath channels.However, system performances with the optimal order are superior to single/multi carrier systems under the doubly selective fading channels. It has the excellent characteristics of the single/multi carrier systems and it is thus prospective in improving the robustness of the communication system.

Keywords:weighted fractional Fourier transform; hybrid carrier system; underwater acoustic environment; optimal order

中图分类号:TN914

文献标志码:A

文章编号:0367-6234(2016)05-0100-05

通信作者:齐洁， qijie@xmu.edu.cn.

作者简介:陈青(1991—),女，硕士研究生;孙海信(1977—)，男，博士生导师.

基金项目:国家自然科学基金(61471309); 福建省自然科学基金(2013J01258).

收稿日期:2014-11-17.

doi：10.11918/j.issn.0367-6234.2016.05.016