一种适于无源LANDMARC算法的定位性能评价方法

史伟光， 韩晓迪， 李建雄， 于　洋， 杜凯旋， 宋战伟

(天津工业大学 电子与信息工程学院， 300387 天津)



一种适于无源LANDMARC算法的定位性能评价方法

史伟光， 韩晓迪， 李建雄， 于洋， 杜凯旋， 宋战伟

(天津工业大学 电子与信息工程学院， 300387 天津)

摘要:针对现有基于无源LANDMARC算法的改进研究主要以提高定位精度为目标，并没有考虑无源半双工通信机制引起的标签读取耗时较长的问题，引入路径损耗公式推导出基于辐射半径的功率能级映射模型. 通过分析阅读器最大功率能级、参考标签布设密度对定位精度及系统耗时的影响，结合多目标优化的联合控制机制，提出一种适用于无源LANDMARC算法的定位性能评价方法. 多种环境下的仿真结果表明，所提评价方法具有良好的稳定性和实用性,对于无源RFID定位系统的参数选择及性能评定具有一定的实际意义.

关键词:射频识别技术; 室内定位； LANDMARC算法； 最大功率发射能级; 定位性能评价方法

射频识别RFID(radio frequency identification)技术是20世纪90年代开始兴起的一种自动识别技术，通过近场耦合或远场耦合方式可以实现阅读器与标签之间的非接触双向数据通信. 相比于传统的条码识别技术，RFID技术无需人工干预即可完成信息的输入和处理，且具有更大的存储容量，因此广泛应用于运输、医疗、防伪、跟踪、设备和资产管理等领域[1-2].

目前，无线室内定位是RFID技术的一个重要应用领域，现有基于RFID的室内定位研究主要围绕LANDMARC系统开展[3-6]. LANDMARC系统的核心思想是通过引入位置固定的有源参考标签动态捕捉环境信息，计算定位标签和参考标签在多个阅读器上的场强欧式距离，依据经验残差算法对近邻参考标签的位置加权，进而完成定位标签的位置估计. 典型的LANDMARC定位系统采用RF Code公司的Spider射频模块搭建，由阅读器和有源标签两部分组成，工作频率为308 MHz. 其中，阅读器具备8个可测功率能级，功率能级1对应最小的识别范围，功率能级8对应最大的识别范围，阅读器通过检测接收到的有源标签的信号强度，完成对定位标签的信息读取等操作.

近年来，得益于无源超高频RFID技术的迅速发展，为进一步降低系统成本、降低标签的体积以增强系统的适用性，越来越多的研究人员搭建了基于915 MHz的无源LANDMARC定位系统，并提出了相应的改进措施. 文献[7]提出一种收信场强矫正机制以剔除无用的参考标签. 文献[8]采用Intel公司的R1000开发平台分析算法性能，因此定位精度较高. 文献[9]充分发挥R1000平台的多路射频端口和二次开发优势，采用多天线复用串行工作方式替代多阅读器并行工作方式进一步降低了系统成本，并提出了动态k值设定机制和误差校正机制.

现有基于UHF RFID的无源LANDMARC定位相关研究主要以提高定位精度为目标，而对定位系统的工作效率分析较少，因此系统性能的评价方式也较为简单，实际指导意义略差. 针对上述问题，本文结合路径损耗模型，依据阅读器最大功率能级、参考标签布设密度对无源LANDMARC算法的定位精度及定位效率进行量化分析，提出一种适用于无源LANDMARC定位系统的定位性能评价方法.

1无源LANDMARC算法的定位原理

现有射频阅读器并不能提供标签的连续、准确的收信场强值，只能依据离散的功率能级提供环境场强信息. 在无源定位初始阶段，阅读器将发射功率调至最大，即以最大功率能级工作，当标签收到阅读器的连续波请求信号后，激活自身电路，并回发应答信号. 阅读器收到应答信号后，逐级降低功率能级，当不能再继续收到标签应答信号时，则认定当前功率能级为标签的收信场强指示. 假设定位环境中共有U个阅读器，依据LANDMARC算法原理，对于第l次定位过程，第i个定位标签的位置可以估计为

(1)

(2)

(3)

式中参数意义如表1所示.

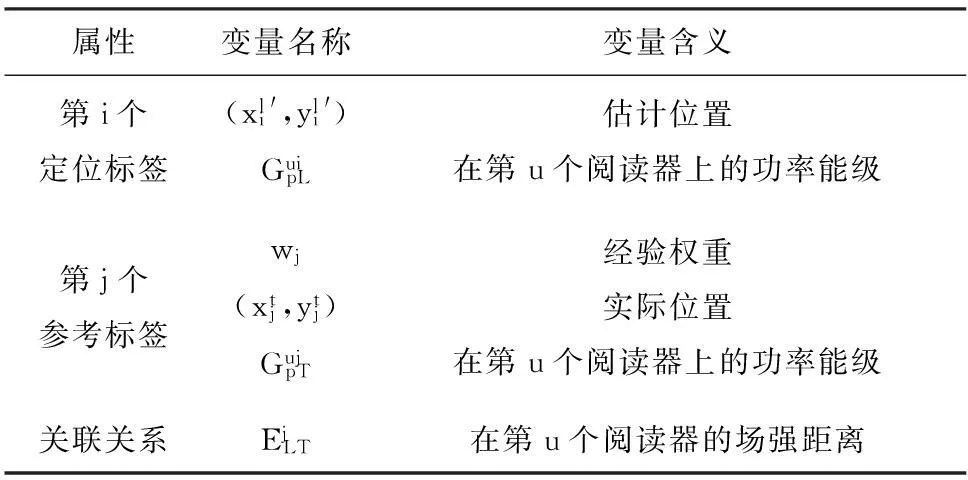
表1　无源LANDAMRAC算法参数设置

2无源LANDMARC算法的定位性能评价2.1基于辐射半径的功率能级映射模型

为研究无源UHF RFID定位系统中功率能级对系统定位性能的影响，依据文献[10]中的式(11)，首先建立基于辐射半径的阅读器功率能级映射模型，可以得到

(4)

式中：Pr表示无源标签接收到的信号功率；Pt表示阅读器的发射功率；R表示Pt对应的读写区域辐射半径；R0表示参考距离；Gr、Gt分别表示阅读器和标签的天线增益；ε表示路径损耗指数，表2列出了典型室内环境下ε的参考值.

表2　室内常见情况下路径损耗指数ε参考值

对式(4)两边取对数运算，可得

(5)

对式(5)展开有

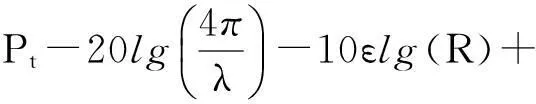
10(ε-2)lg(R0)+Gr+Gt.

(6)

(7)

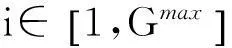
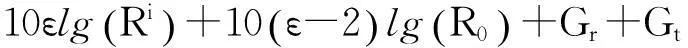
(8)

针对室内环境中由人为扰动和障碍物阻挡引起的幅度衰落，使得无源标签收信功率降低进而造成的漏读现象，本文引入服从正态分布、期望为0、标准差为σ的高斯白噪声Xσ对式(5)中的无源标签收信功率进行修正，从而有

(9)

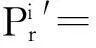
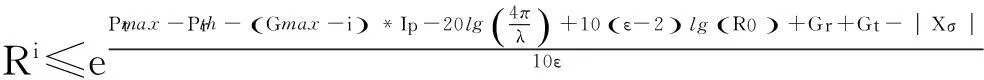
为便于分析说明，本文以自由空间为例，由表2令ε=2，则有

2.2无源LANDMARC算法的定位精度评价

以系统完成L次定位服务的估计误差均值AEtol为指标，来评价定位算法的性能. AEtol越小，即定位精度越高. 显然有

2.3无源LANDMARC算法的定位效率评价

以系统对C个定位标签完成L次定位服务的系统耗时均值Ttol为指标，来评价无源LANDAMRC系统的定位效率. Ttol越小，定位速度越快，则单位时间内完成定位功能的标签数量越多，即定位效率越高.

显然有

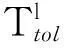
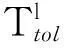
表3　定位环境参数设置

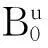
典型的时隙ALOHA算法在纯ALOHA算法基础上将时间分成多个离散时隙，标签在响应过程中选择不同的时隙向阅读器发送数据，当单个时隙中仅有一个标签发送数据时，则该标签被阅读器成功识别. 各时隙存在碰撞、空闲、成功3种可能状态，分别代表该时隙内有多个标签响应、无标签响应、唯一标签响应.

不同于有源RFID系统可以采用标签先发言的单工通信机制，无源UHF RFID通信必须采用基于阅读器先发言的半双工通信机制，阅读器读取全部标签的耗时主要受阅读器请求时间tE和时隙响应时间tD影响[12]. 则对于耗时函数有

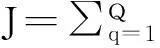
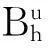
在上述调整功率过程中，第u个阅读器的读取标签耗时可以记为Tru，且有

相应地，第u个阅读器的功率能级切换耗时可以记为Tzu，且有

步骤4上位机系统依据各阅读器关于参考标签和定位标签的功率能级信息，依据式(1)～(3)得定位标签的估计位置.

综上，无源RFID定位系统完成一次定位服务的耗时可以描述为

式中:Tc为系统对C个定位标签执行LANDMARC算法运算的耗时，Tz为系统中全部阅读器功率能级调整的综合耗时，Tr为系统中全部阅读器读取标签的综合耗时.

对于Tc，显然有

Tc=C*tc.

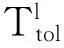
若系统采用并行方式工作，则有

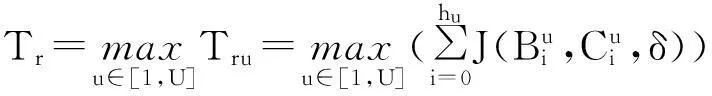
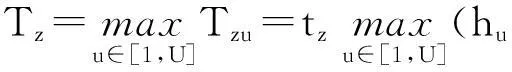
(10)

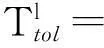
(11)

若系统采用串行方式工作，则有

(12)

(13)

由式(11)、式(13)可知，在定位标签数目一定的前提下，阅读器的最大功率能级和参考标签布设密度将直接影响系统耗时，采用复用串行方式尽管能够降低系统成本，但却以更大的系统耗时为代价.

2.4基于联合控制机制的品质函数构建

结合文献[14]中的全局优化目标函数的构建方法，本文采用联合控制机制，以估计误差均值最小化、系统耗时均值最小化为目标，构建适于评价无源LANDMARC算法的定位性能品质函数为

(14)

需指出，权重系数的选取至关重要，并决定估计误差和系统耗时在定位性能品质函数中的比重. 本文分别引入CWA(conventional weight aggregation典型权重聚焦)算法和DWA(dynamic weight aggregation动态权重聚焦)算法实现权重系数的优化选取.

2.5基于CWA/DWA算法的权重系数选取

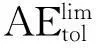
(15)

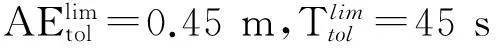
然后选取DWA算法对式(15)中的权重系数的关系进行性能评价. DWA算法的核心思想是通过优化过程中目标函数的权重系数的周期性变化以得出帕雷托边界曲线. 需指出，帕雷托边界曲线是DWA算法中判断权重系数是否为最优值的重要标准. 帕雷托边界是指在某种既定的资源配置状态下，任何改变都不可能使当前的状况变好或变坏. 满足帕雷托最优状态标准的资源配置可以被认为是最优配置方法.

依据DWA算法寻优机理，令权重系数按式(16)、(17)周期变化，以获得基于帕雷托边界的多种权重系数配置方式[16]：

(16)

(17)

其中F表示权重系数变化的频率，f表示权重系数的寻优尺度. 令F=200，f=0,1,2,…,200，则可得到如图1所示的f/F和k1(f)/k2(f)的关系. 结合图1中呈现的周期性和对称性，为提高仿真运行效率，在本文仿真分析中限定f的最大值为F/4.

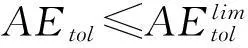
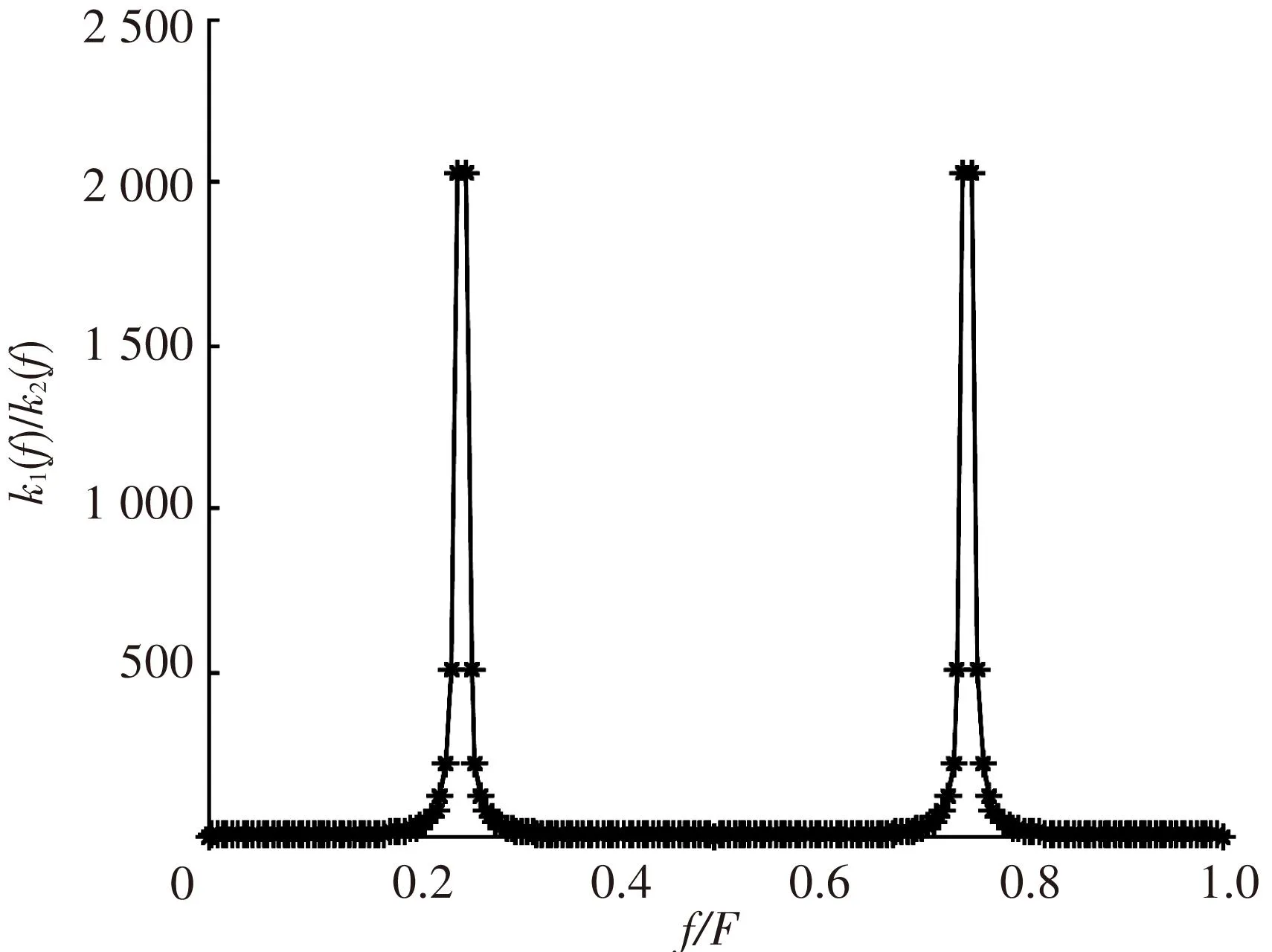
图1　DWA算法中f/F和k1(f)/k2(f)的关系

3仿真分析

表4　仿真参数设置

3.1权重系数选取分析

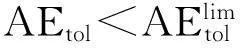
3.2基于品质函数的性能评价

依据图2结论，选取0.3≤σ≤2的室内环境进行分析，得到两种工作方式的品质函数表达式为

(18)

(19)

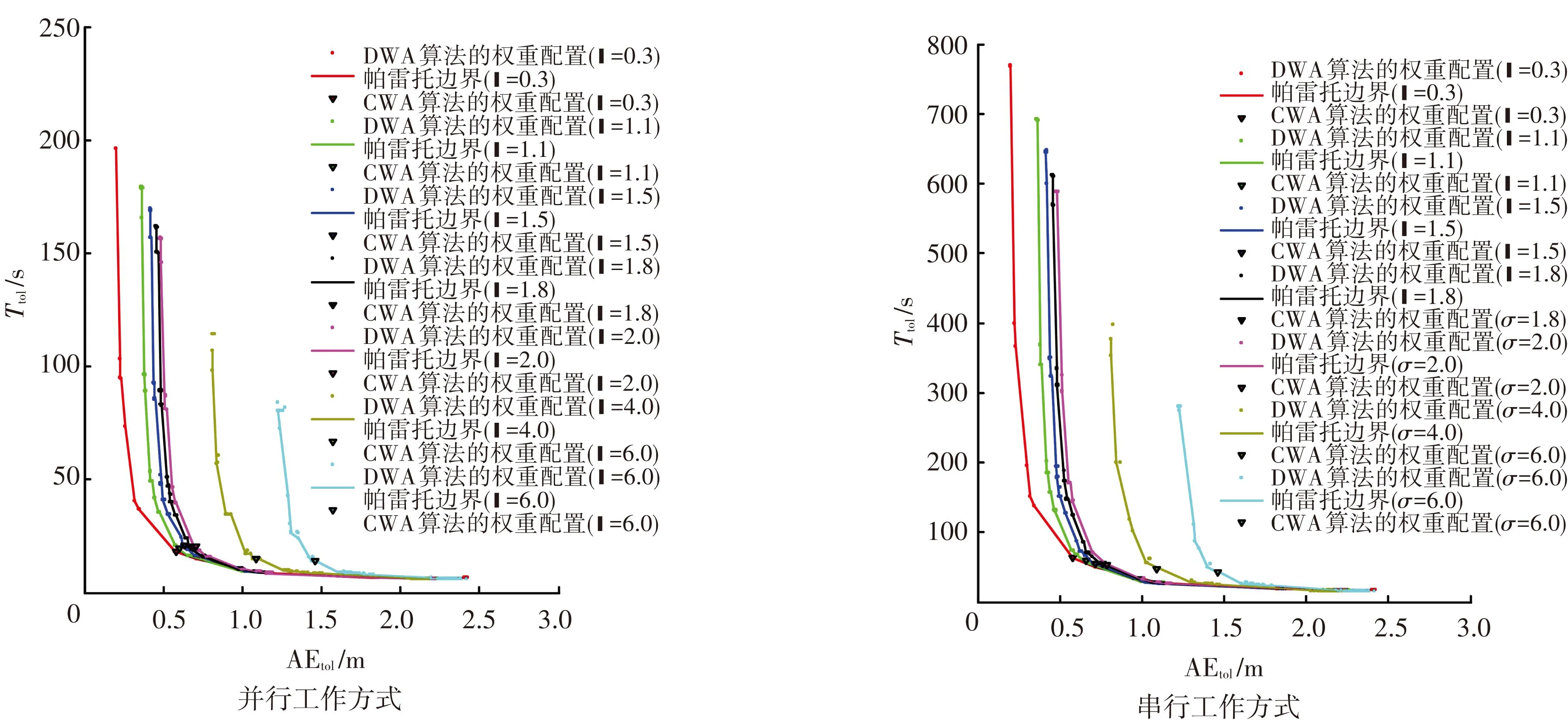
图2　权重系数配置及帕雷托边界

表5反映了基于式(18)、式(19)得到的多噪声环境下的最优资源配置方式及系统性能. 分析可知，对于并行工作方式，随着环境噪声的逐渐增大，最优参考标签排列方式由8×8提高为9×9以缓解收信功率失真对定位精度的影响，并在σ∈[0.3,2]区间内稳定在10×10均匀排列. 尽管在上述渐变过程中，参考标签数量由64增大至100会增加系统耗时，但最优Gmax始终稳定在16，将Ttol始终控制在[18.15,20.61]范围内，并满足40 s的上限要求. 对于串行工作方式，随着环境噪声逐渐增大，最优Gmax仍稳定在16，而最优参考标签排列方式由8×8降低为7×7，上述变化趋势与并行工作方式显然相同. 对比式(10)和式(12)可知，串行工作方式中的阅读器采用时分复用方式调用系统射频通信资源，叠加效应使得系统耗时随参考标签布设密度的提升而急剧加大. 以σ=1.5为例，当ρ=10、Gmax=16时，并行工作方式下达到最优性能且Ttol=19.25 s，若串行工作方式也采用上述资源配置方式，其系统耗时将逼近80s的上限要求，而若采用参考标签7×7方式排列，其系统耗时将控制在55 s，远低于80 s的上限要求.图3反映了多种噪声环境下两种工作模式下的估计误差和系统耗时均值的累计分布函数CDF(cumulative distribution function)曲线性能. 在多种噪声环境下，两种工作模式的CDF曲线平滑，反映出本文建立的定位精度评价模型和定位效率评价模型具有良好的稳定性和适应性. 以σ=1.1为例，对于并行工作方式，估计误差的最小值为0.382 6 m，以92.33%的概率低于0.7 m，系统耗时的最小值为15.9340 s，以100%的概率低于40 s；对于串行工作方式，估计误差的最小值为0.4316 m，以94%的概率低于0.8 m，系统耗时的最小值为45.12 s，以100%的概率低于80 s.

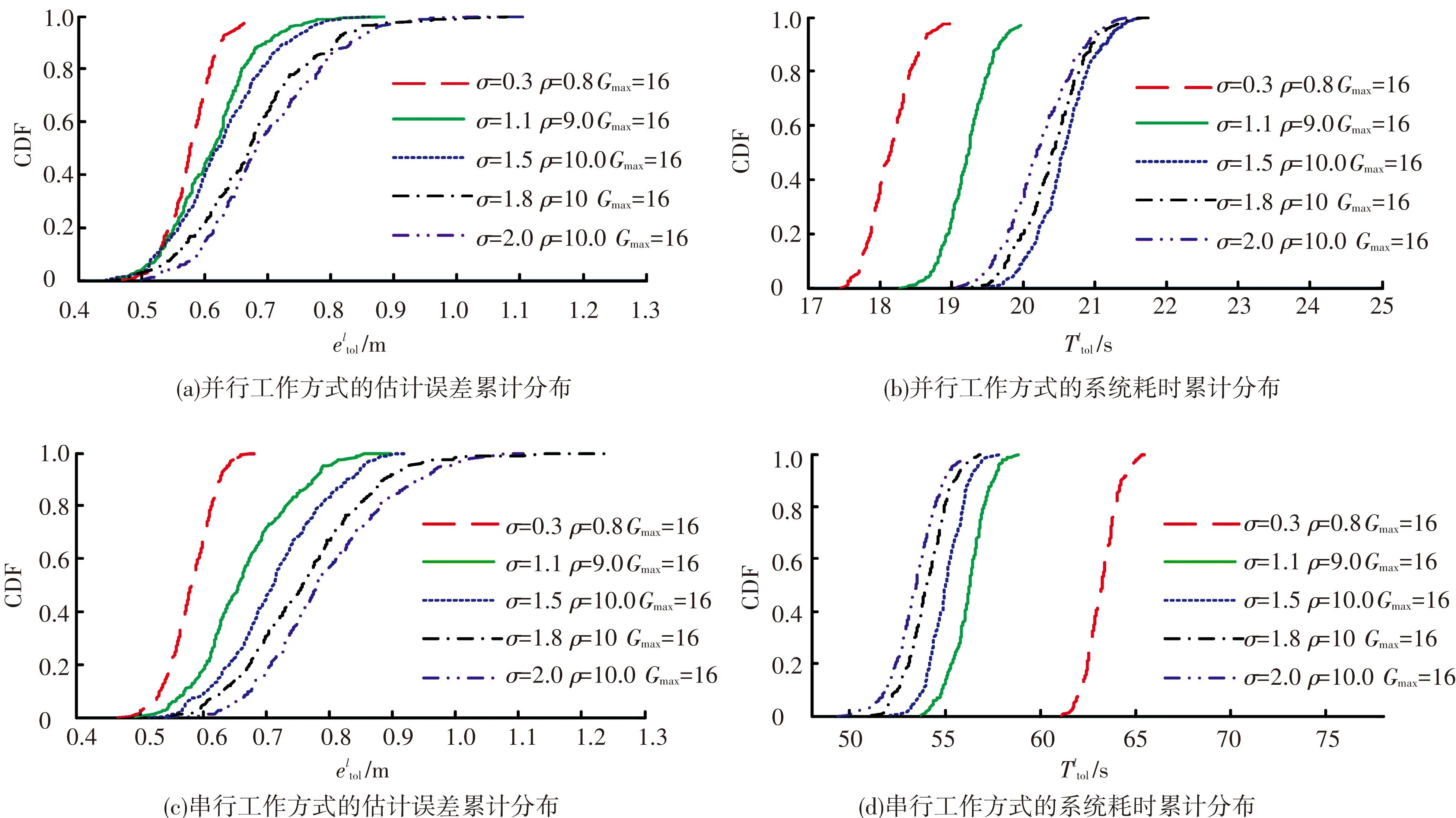
图3　两种工作模式下的估计误差和系统耗时的累计分布函数

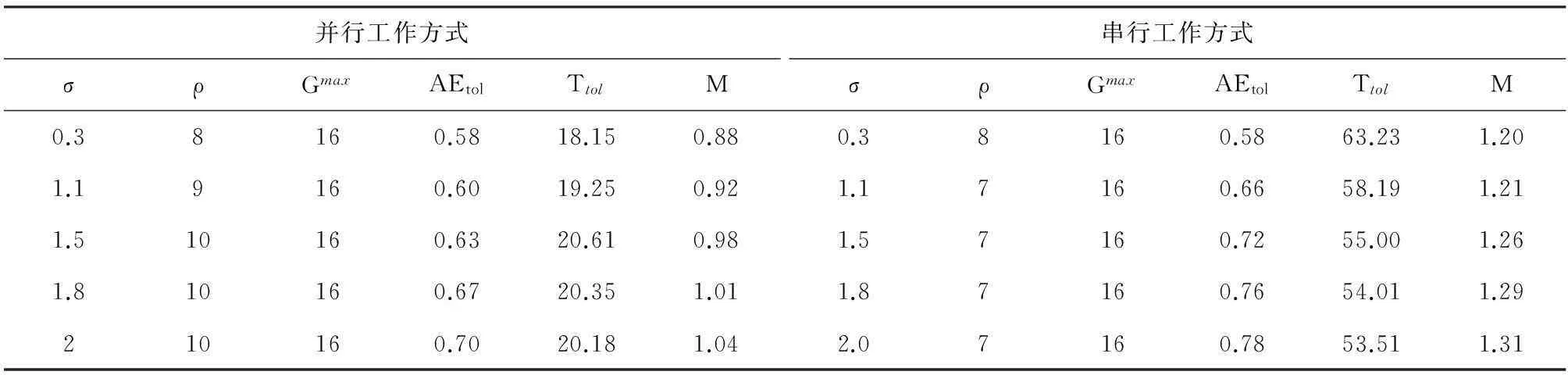
并行工作方式σρGmaxAEtolTtolM串行工作方式σρGmaxAEtolTtolM0.38160.5818.150.880.38160.5863.231.201.19160.6019.250.921.17160.6658.191.211.510160.6320.610.981.57160.7255.001.261.810160.6720.351.011.87160.7654.011.29210160.7020.181.042.07160.7853.511.31

综上，并行工作模式以提高系统成本的方式降低系统耗时，而串行工作模式以时分复用方式提高资源的利用率，降低系统成本要求，但系统耗时急剧增加，且在环境噪声较大的环境中，系统不得不降低参考标签布设密度以牺牲定位精度来换取系统耗时，从而保证全局定位性能的最优，显然这一结论与实际应用情况吻合.

4结语

针对现有基于无源LANDMARC算法的改进研究主要采用定位误差评价系统性能，而没有考虑无源半双工机制引起的系统效率较低的问题，本文结合路径损耗模型，通过分析阅读器最大功率能级、参考标签布设密度对定位精度及定位实时性的影响，构建系统耗时模型，并以估计误差均值的最小化、系统耗时均值的最小化为目标，引入基于联合控制机制构建的品质函数，同时采用CWA算法和DWA算法选取权重系数，提出了一种适用于无源LANDMARC算法的定位性能评价方法. 多种噪声环境中的仿真结果表明，所提评价方法对于无源RFID定位系统的参数选择及性能评定，具有一定的指导意义.

参考文献

[1] ZHOU J, SHI J. RFID localization algorithms and applications—a review [J]. Journal of International Manufacturing, 2008, 20(6):695-707.[2] SANPECHUDA T, KOVAVISARUCH L. A review of RFID localization: applications and techniques [C]//Proceeding of the 5th International Conference on Electrical Engineering/Electronics, Computer, Telecommunications and Information Technology. Krabi: IEEE, 2008:769-772.

[3] NI L M, LIU Y, LAU Y C, et al. LANDMARC: indoor location sensing using active RFID[J]. Wireless Networks, 2004, 10(6):701-710.

[4] ZHAO Yiyang, LIU Yunhao. VIRE: Active RFID-based localization using virtual reference elimination[C]//Proceeding of International Conference on Parallel Processing. Xi’an: IEEE, 2007:56.

[5] 史伟光,刘开华,于洁潇,等.基于加权欧式算子的射频识别定位算法[J].计算机工程, 2011, 37(9): 22-24,28.

[6] HAN K, CHO S H. Advanced LANDMARC with adaptive k-nearest algorithm for RFID location system [C]//Proceeding of the 2nd IEEE International Conference on Network Infrastructure and Digital Content. Beijing: IEEE, 2010: 595-598.

[7] CHOI J S, LEE H, ELMASRI R, et al. Localization systems using passive UHF RFID [C]//Proceeding of 5th International Joint Conference on INC, IMS, and IDC. Seoul: IEEE, 2009:1727-1732.

[8] KHAN M A, ANTIWAL V K. Location estimation technique using extended 3-D LANDMARC algorithm for passive RFID tag[C]//Proceeding of International Advance Computing Conference. Patiala: IEEE, 2009: 249-253.

[9] 王远哲,毛陆虹,刘辉,等.基于参考标签的射频识别算法研究与应用[J].通信学报, 2010, 31(2): 86-92.

[10]任智,李晴阳,陈前斌.无线网络衰落和损耗的建模与仿真研究[J].系统工程与电子技术, 2009, 31(12): 2813-2819.

[11]佐磊,何怡刚,李兵,等.无源超高频射频识别系统路径损耗研究[J].物理学报, 2013, 62(14): 150-157.

[12]CHEN W. A feasible and easy-to-implement anticollision algorithm for the EPCglobal UHF class-1 generation-2 RFID protocol [J]. IEEE Transactions on Automation Science and Engineering, 2014, 11(2):485-491.

[13]SCHOUTEF C. Dynamic frame length ALOHA [J]. IEEE Transactions on Communications, 1983, 31(4):565-568.

[14]MANMUEL L, JAVIER O R, ANTONIO R J, et al. Diversified local research for the optimal layout of beacons in an indoor positioning system [J]. IIE Transactions, 2009, 41(3):247-259.

[15]FLEMING P J. Computer aided control systems using a multi objective optimization approach [C]//Proceeding of IEEE Control’85 Conference. Cambridge: IEEE, 1985:174-179.

[16]JIN Y, OLHOFER M, SENDHO B. Dynamic weighted aggregation for evolutionary multi-objective optimization: why does It work and how?[C]//Proceeding of the Genetic and Evolutionary Computation Conference. San Francisco: ACM, 2001:1042-1049.

(编辑王小唯苗秀芝)

A performance evaluation mechanism suitable for passive LANDMARC algorithm

SHI Weiguang, HAN Xiaodi, LI Jianxiong, YU Yang, DU Kaixuan, SONG Zhanwei

(School of Electronic and Information Engineering, Tianjin Polytechnic University, 300387 Tianjin, China)

Abstract:Considering most advanced LANDMARC algorithms based on passive RFID mainly aimed at enhancing the accuracy of the localization but neglecting the long time consumed in reading tags because of the by half-duplex mechanism, we leverage the distance loss formula and put forward power level model based on the radiation radius. After analyzing the influences of the maximum power grades of the RF reader and the arrangement density of the reference tags, an evaluation method of localization is proposed for the passive LANDMARC algorithm. Simulation results in a wide range of environments showed that the proposed method has the good stability and practicability. The method also makes sense of system evaluation and parameter selection for the passive RFID Localization Algorithms.

Keywords:radio frequency identification; indoor location; LANDMARC algorithm; maximum emission level; evaluation method of location performance

中图分类号:TN925.93

文献标志码:A

文章编号:0367-6234(2016)05-0127-07

通信作者:史伟光，shiweiguang12345@126.com.

作者简介:史伟光(1985—)，男，博士，讲师.

基金项目:国家自然科学基金(61372011).

收稿日期:2015-05-30.

doi：10.11918/j.issn.0367-6234.2016.05.021