超塑性自由胀形温度对Ti2AlNb板材壁厚分布的影响
马俊林, 刘雨生, 李 萍, 薛克敏
(合肥工业大学 材料科学与工程学院,230009 合肥)
超塑性自由胀形温度对Ti2AlNb板材壁厚分布的影响
马俊林, 刘雨生, 李萍, 薛克敏
(合肥工业大学 材料科学与工程学院,230009 合肥)
摘要:为研究Ti2AlNb合金高温超塑性自由胀形时的壁厚分布规律,对初始厚度均匀的Ti2AlNb板材进行有限元模拟和试验研究. 在胀形温度分别为910、930、950和970 ℃时,采用恒应变速率法对最终胀形试样的壁厚分布进行数值模拟,研究了胀形后试样的壁厚分布规律. 结果表明:Ti2AlNb板材在胀形后曲面壁厚分布不均匀,易呈现出不规则球形;胀形温度对曲面形状和壁厚具有较大的影响,变形温度对Ti2AlNb板材超塑性自由胀形壁厚分布影响较大. 在此基础上,引入温度敏感性指数n,对预测胀形壁厚的E-K模型进行修正. 研究结果为Ti2A1Nb合金在航空航天复杂薄壁结构件的超塑成形提供一定的参考依据.
关键词:超塑性自由胀形; Ti2AlNb合金; 壁厚分布; 温度; 有限元
Ti2AlNb是以有序正交结构O相为基础的金属间化合物合金(简称为Ti2AlNb基合金),由于长程有序的超点阵结构减弱了位错运动和高温扩散,因而该合金不仅具有较高的高温抗拉强度、室温塑性和疲劳强度,而且抗氧化性、抗高温蠕变性能良好[1-3]. Ti2AlNb合金作为高密度镍基高温合金的替代材料被寄予极大的期待[4-5].
板料超塑胀形是利用板料在超塑性状态下具有的良好成形性,可以一次成形出传统工艺难以实现、形状复杂的零件,被广泛应用于航空航天、机械制造等工业领域[6-7]. 目前,对普通钛合金超塑性变形机制和基于有限元的材料变形行为数学模型等的研究较多,利用超塑性自由胀形技术制造Ti2A1Nb合金薄壁结构零件的研究仍处于起步阶段[8-10]. 文献[11]对粗晶态Ti2AlNb合金的超塑性行为进行了试验研究,系统研究了Ti2AlNb合金在1213~1263 K内的超塑性变形机制,并得到本构方程. Enikeev和Kruglov[12](E-K模型)假设材料为各向同性的均质材料,并且在胀形过程中中间剖面呈标准椭圆形或圆形,计算得到厚度解析式.
本文采用有限元模拟与试验相结合的方法,对Ti2AlNb合金在910 、930 、950 和970 ℃下的超塑胀形工艺进行研究,分析不同成形温度下最终胀形试样的厚度分布规律,获得了最佳的超塑胀形成形温度,并修正了钛合金自由胀形预测壁厚的E-K模型,对促进Ti2AlNb合金结构件的工业应用具有指导意义.
1试验
试验所用材料为O相基合金Ti2AlNb合金化热轧态板材,板材尺寸为140 mm×140 mm×1.0 mm,密度为5.28 g/cm3,极限抗拉强度为1126 MPa,其化学成分如表1所示. 经过热处理后,晶粒尺寸只有5 μm左右,并且合金中含有体积分数相近的α2/O相和B2相,在变形中能相互制约来抑制晶粒的长大,如图1所示. 因此,该Ti2AlNb基板材具有良好的超塑性性能,可以满足自由胀形试验要求. 采用压力可控的气压胀形设备进行超塑性自由胀形试验,通过加热设备保证板材在各温度下恒温变形,胀形部分的板材直径为110 mm.

表1 Ti2AlNb合金的化学成分 wt.%

图1 初始Ti2AlNb板材组织
2有限元模拟
2.1力学模型
超塑性材料是应变速率敏感性材料,变形过程呈稳态变形,一般可忽略应变硬化现象. 超塑成形的流变方程为[13]
(1)
基于SPF模块的MSC.MARC可以很好地模拟板材的超塑性变形过程,方程(1)对应于MARC中的POWER LAW准则:
其中,B和N的值对应于式(1)中的K和m的值.
温度/℃延伸率/%mK9101450.243559301600.304609501750.4210009701300.13100
2.2几何模型
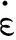
2.3基本假设
相比普通塑性变形过程,超塑性变形过程更为复杂,涉及到材料非线性、几何非线性等诸多问题. 为便于有限元模拟研究,对Ti2AlNb板材超塑性自由胀形作如下假设:
1)板材采用理想刚塑性材料模型,不考虑弹性变形的影响,模具定义为刚性.
2)在胀形过程中的各个温度参数保持恒定不变.
3)材料体积不变且各向同性,忽略超塑成形中的应变硬化效应.
4)板材和模具在整个过程不发生侵入和贯穿现象.
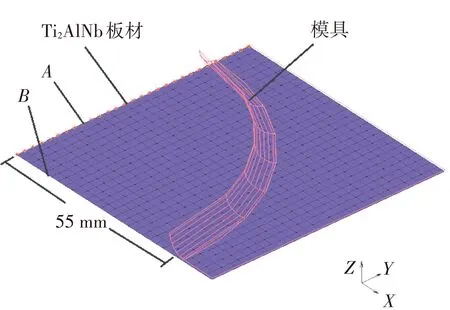
图2 几何模型
2.4摩擦与边界条件
超塑性自由胀形过程是未被模具压边的坯料不断胀形的过程. 在数值分析中,坯料与模具接触的部分计算距离公差、摩擦力等,本文采用库伦摩擦模型[15]. 考虑试验的工况条件,摩擦因子取0.3.
定义板材和模具边缘节点的x、y、z方向位移为0,定义对称面A和B处分别在x和y方向的位移为0,如图2所示. 对板材所有单元施加面载荷,压力方向均指向模具,并定义为跟随力,在成形过程中压力方向始终垂直于单元.
3结果及讨论
3.1模拟结果
各温度下有限元模拟设置的参数只是m和K的值不同,因此各温度下模拟的板材胀形壁厚分布规律也较相似,故以950 ℃胀形的模拟结果为例. 如图3所示,Ti2AlNb板材在950 ℃下胀形至最终阶段时(t=3 000 s),曲面顶点处板料厚度为0.324 mm,最大减薄率达到67.6%. 模拟结果显示,胀形至饱满曲面时,曲面最薄处位于曲面最顶点,板材厚度自曲面底部边缘至曲面顶点呈梯度减小. 在后处理中,根据最大应变速率控制法可以自动计算出各温度胀形的压力-时间曲线(如图4所示),这为后期试验的压力加载提供了参考,有利于减少胀形时间,得到壁厚分布均匀的样件.
3.2试验结果
试验在910、930、950和970 ℃下的极限胀形最大气压分别为2.6、2.0、2.0和1.6 MPa. 由于忽略材料本身组织和性能的不均匀等影响,与图4的模拟结果相比,试验胀形气压偏大. 极限胀形后的试样如图5所示,随着胀形温度的增加,球形越饱满,表明变形温度越高,Ti2AlNb合金胀形可变形程度越高. 在胀形的最终阶段,曲面减薄严重,在靠近球顶处产生破裂,导致最终曲面形状不规则. 根据投影法,测得各胀形温度下的α角分别为73°、76°、90°和90°,说明Ti2AlNb板材的可胀形程度随变形温度的升高而不断增大. 如图6所示,随变形温度逐渐增加,板材的最终胀形高度不断增大,曲面顶点处厚度反而越小. 表明较高的胀形温度有利于Ti2AlNb合金超塑性的发挥. 为了准确研究Ti2AlNb板材超塑性自由胀形最终壁厚分布的规律,沿胀形后试样中间剖面,每隔弧度5 mm做标记. 每个点附近使用游标卡尺测量三次,取平均值为该点壁厚的试验值.
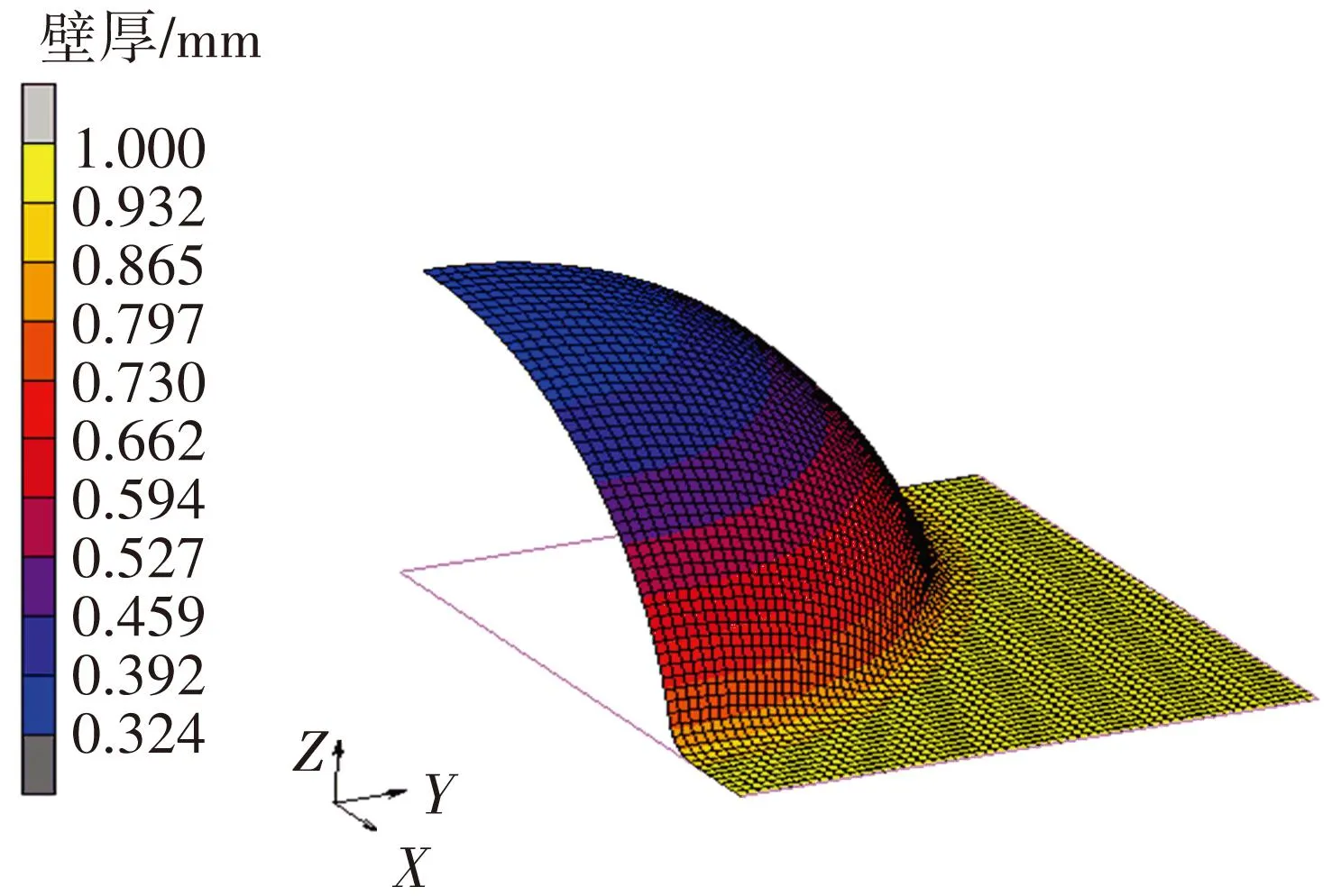
图3 950 ℃时胀形模拟结果(t=3 000 s)
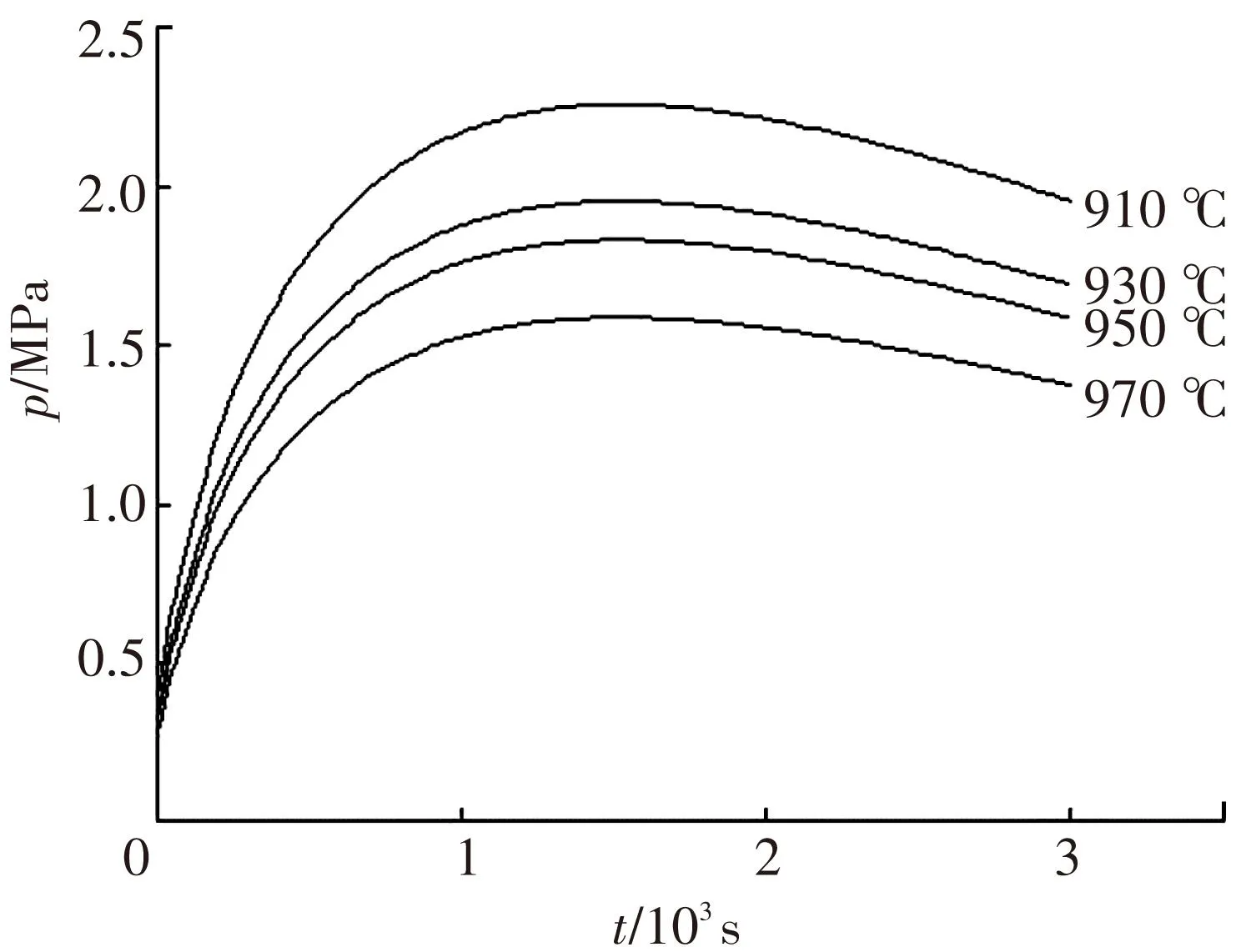
图4 压力-时间曲线
图7所示为各胀形温度下Ti2AlNb板材胀形的试验测量、有限元模拟和E-K预测模型计算的壁厚沿曲面的分布结果. 可以发现,对于整个曲面壁厚分布,有限元模拟结果和试验结果比较吻合,特别是在曲面顶点区域和曲面底部区域吻合最好,原因是有限元模拟时考虑了温度的影响(不同温度下的m和K值). 模拟结果表明,有限元模拟可以为Ti2AlNb板材超塑性自由胀形后曲面壁厚分布提供一定的参考. 而E-K模型在910~970 ℃内的计算结果与试验结果误差较大,说明E-K模型不能够准确预测Ti2AlNb板材在910~970 ℃内低应变速率自由胀形的壁厚分布情况.

(a) T=910 ℃

(b) T=930 ℃

(c) T=950 ℃

(d) T=970 ℃
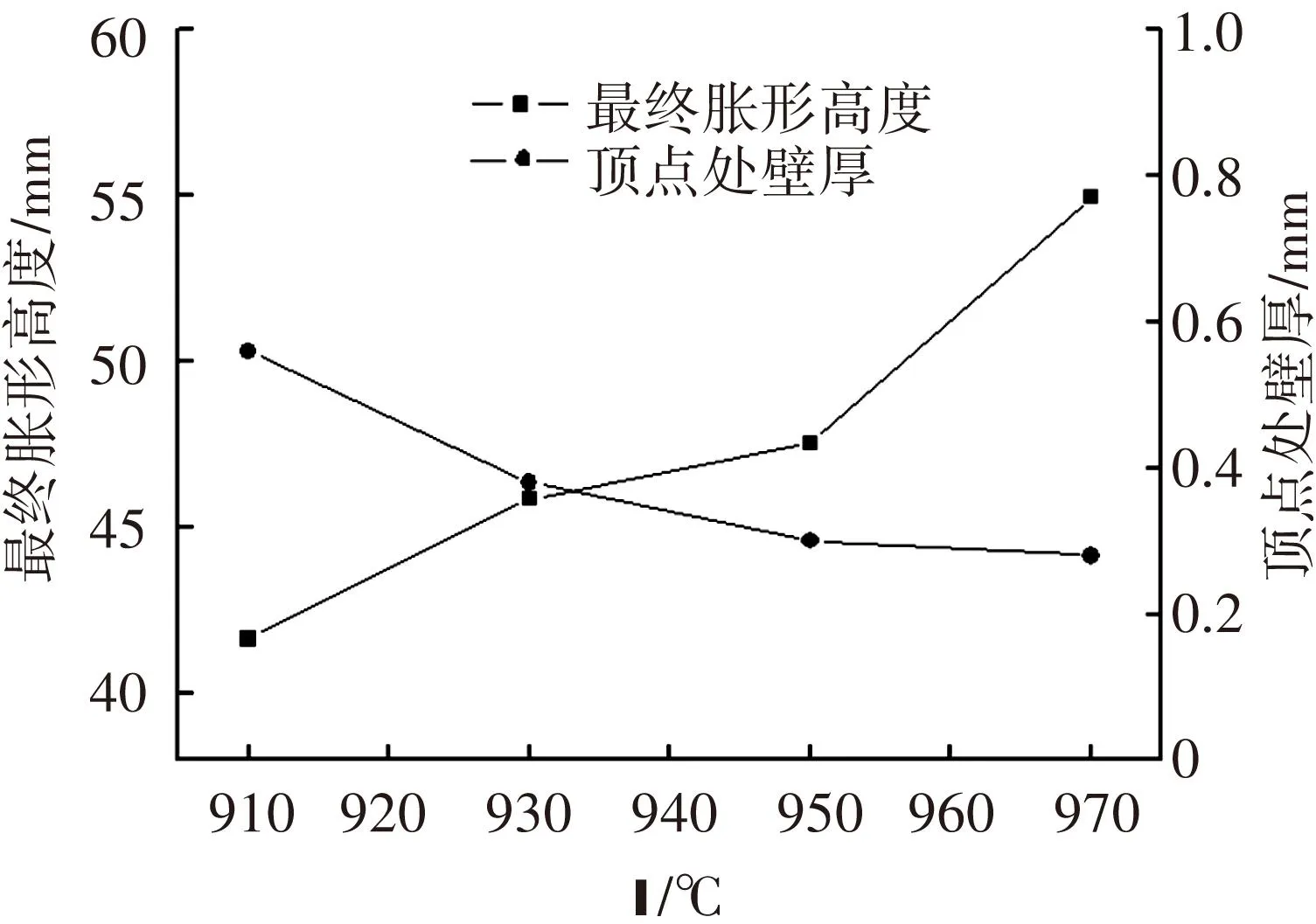
图6 试样最终胀形高度和顶点处的壁厚
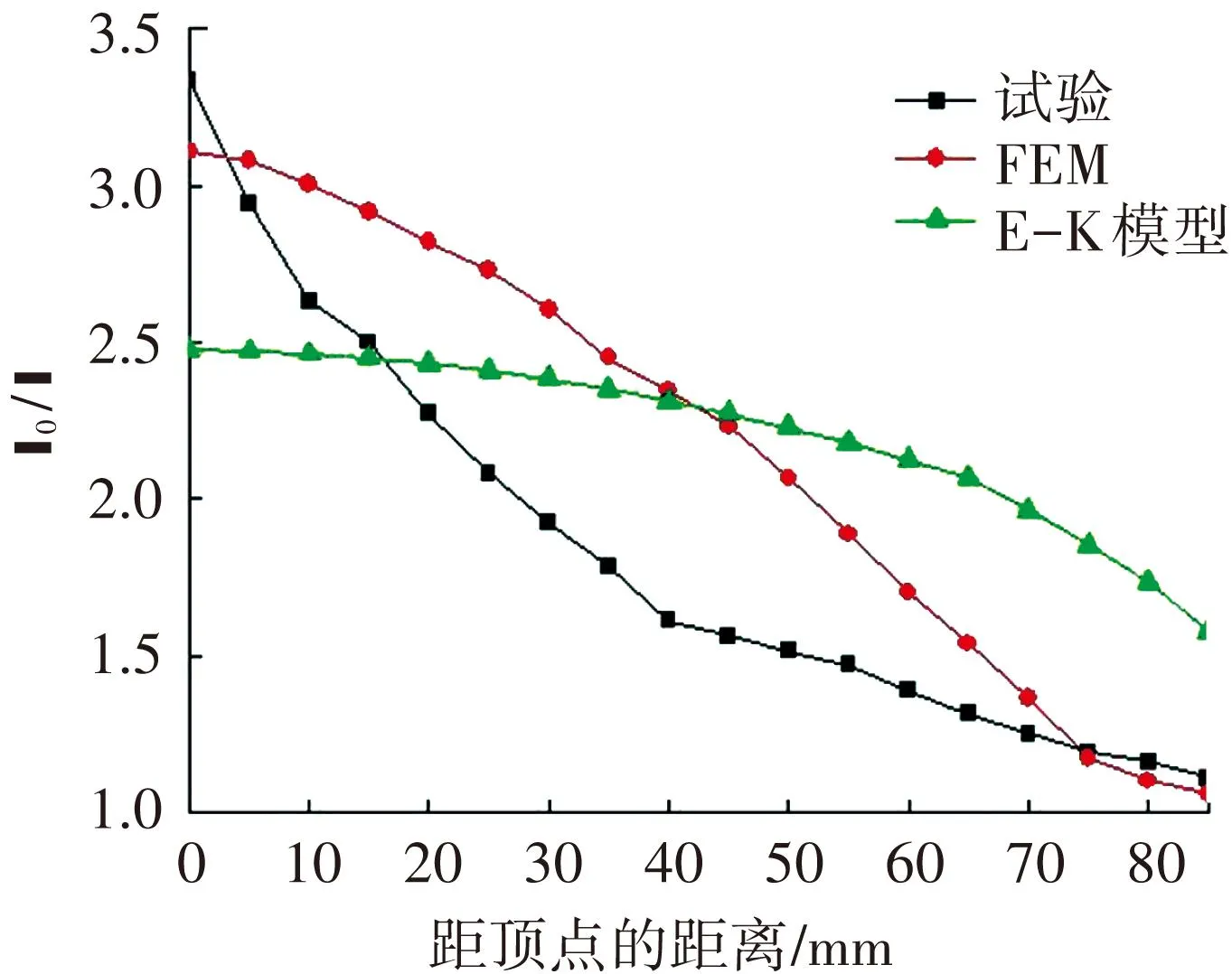
(a) T=910 ℃
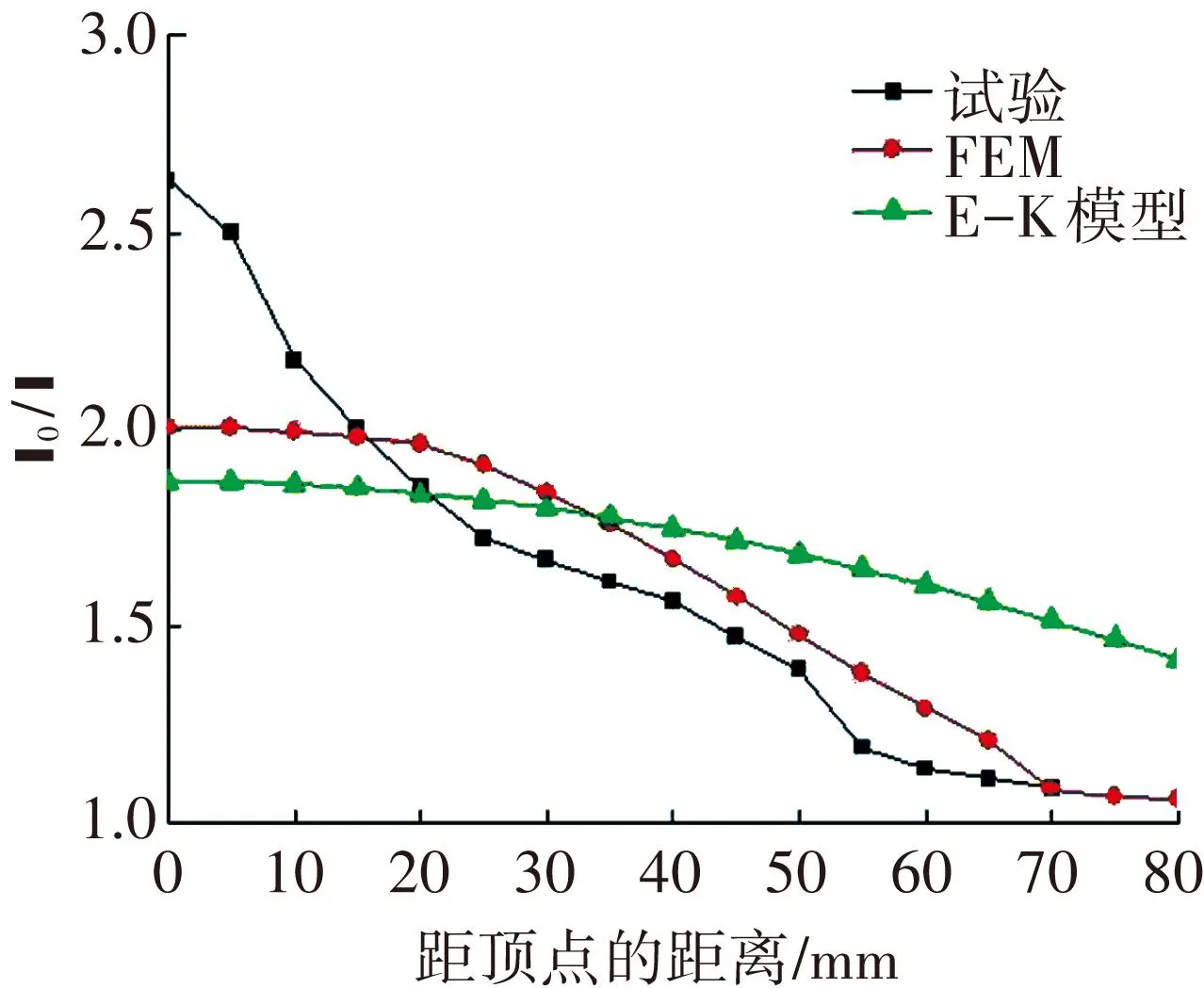
(b) T=930 ℃
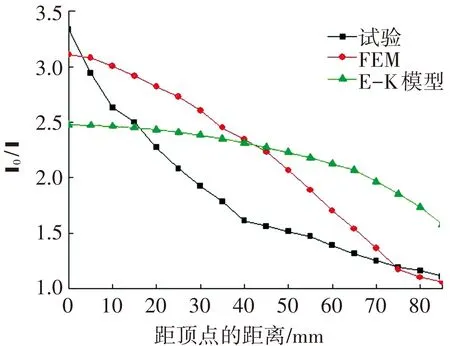
(c) T=950 ℃
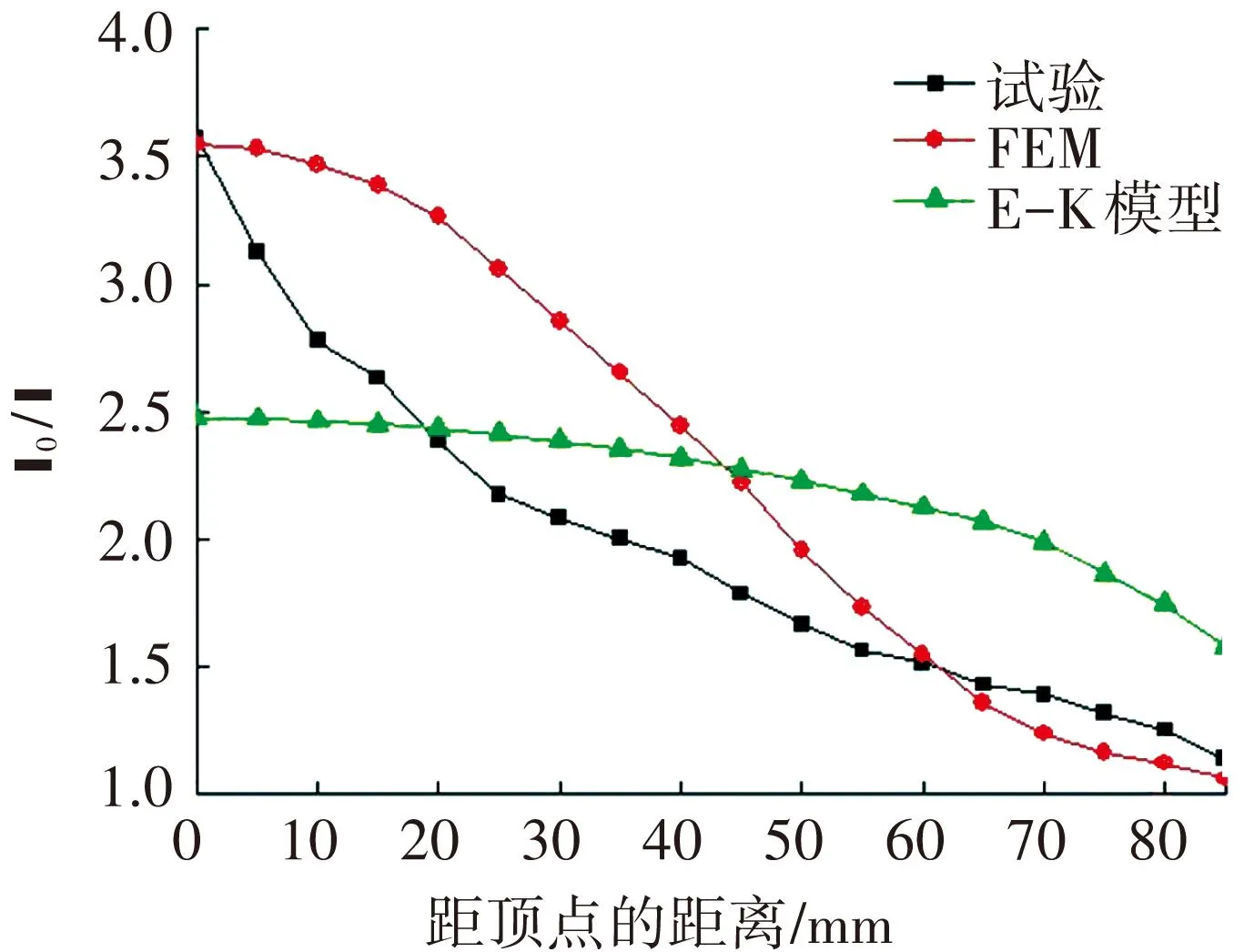
(d) T=970 ℃
3.3讨论
钛合金在高温变形时流动应力和温度之间满足包含激活能和温度的双曲正弦关系[16]. 根据表2,变形温度对Ti2AlNb合金的超塑性变形影响较大,表明该材料在超塑性变形过程中具有温度敏感性的特征. 而E-K预测模型没有考虑变形温度对超塑性胀形壁厚分布的影响,而且实际胀形过程中曲面各点的应变速率各不相同,这些因素都会导致Ti2AlNb板材试验的壁厚分布情况与数学模型预测结果之间产生较大的误差.
通常,温度敏感性指数n表达式如下[17]:
(2)
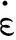
为研究温度对Ti2AlNb合金胀形的影响,在已确定的应变速率的基础上,根据课题组已有的研究成果,得到σ-T曲线,如图8所示. 对图9中的数据点进行线性拟合,计算拟合直线的斜率,得到Ti2AlNb合金在910~970 ℃内的n=0.364.

图8 Ti2AlNb合金的σ-T曲线
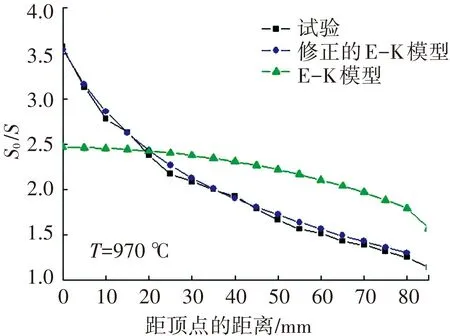
图9 E-K模型修正前后的比较
E-K模型胀型原理如图10所示[12],在胀形前板材上的一点M,在胀形的某一阶段会移至M′点. Enikeev和Kruglov[12]研究发现,经过M′点的曲面经线胀形α角后被拉长(α/sinα)倍,经过M'点的曲面纬线会被拉长ρ/ρ0倍,得到曲面M'点的厚度为(假设材料不可压缩)
(3)
但是,Enikeev和Kruglov并没有考虑温度对金属材料胀形时的影响,随着胀形温度的提高,金属材料会不断软化. 因此,M′点在经线方向或是纬线方向上,其被拉伸的程度可能会更高. 并且沿M′点经线方向,自曲面顶点至边缘处,温度对这种拉伸作用的影响越来越小. 为了衡量胀形温度对壁厚分布的影响,引入温度敏感性指数n,则式(3)可表示为
(4)
式中: ρ和ρ0分别为M点和M'点的水平坐标;系数a、b和c是与材料、胀形温度有关的常数,可根据具体胀形工艺参数确定.
根据图10中的几何关系可知
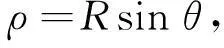
(5)
(6)
结合式(4)~(6),得到修正后的E-K模型表达式为
取温度T=970 ℃,在此温度下,a=0.60,b=1.54,c=0.95,得到Ti2AlNb合金在970 ℃胀形时的壁厚分布模型. 如图9所示,与E-K模型相比,修正后的E-K模型对实际胀形壁厚分布的预测更加准确.
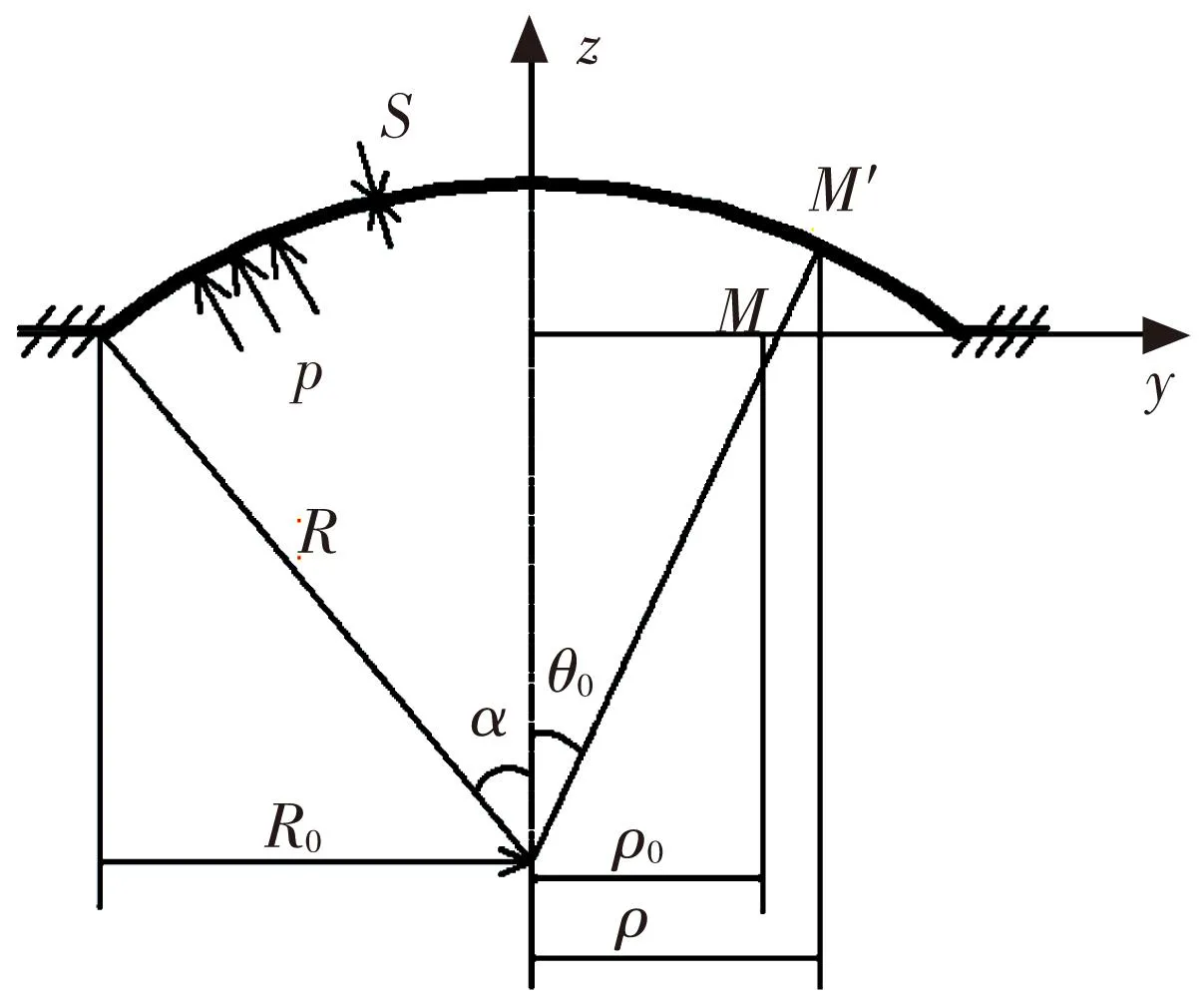
图10 胀形原理示意
4结论
1)在整个曲面区域,模拟结果和试验结果吻合较好,原因是有限元模拟设置不同温度下m和K的值,考虑了胀形温度的影响. 因此,有限元模拟可以为Ti2AlNb合金在该温度范围内的超塑性极限自由胀形的壁厚分布提供一定的参考.
2)较低的胀形温度易导致Ti2AlNb合金流动变形困难,m的值较小,难以在胀形时产生超塑性变形,容易破裂;较高的胀形温度有利于发挥该Ti2AlNb合金的超塑性性能,但曲面顶点处的壁厚减薄严重,易产生破裂.
3)在910~970 ℃内,E-K模型计算结果与试验结果相差较大,主要原因是E-K模型没有考虑胀形温度的影响,E-K模型不能准确预测Ti2AlNb合金在该温度范围内的超塑性自由极限胀形壁厚分布情况;引入温度敏感性指数对E-K模型进行修正,修正的E-K模型预测结果与试验的壁厚分布情况吻合较好,可以为预测Ti2AlNb合金在910~970 ℃内的胀形壁厚分布情况提供较好的参考.
参考文献
[1] DAI Jingru, LU Huimin, CAI Zhijin. Effect of erbium addition on microstructre of As-Cast Ti-22Al-25Nb alloy[J]. Materials Processing and Interfaces, 2012, 1: 955-961.
[2] BRAUN R, LEYENS C. Protective coatings on orthorhombic Ti2AlNb alloys[J]. Materials at High Temperatures, 2005, 22(3/4): 437-447.
[3] WU H Y,ZHANG P Z,XU Z. Study on nanomechanical and high temperature tribological behaviour of Ti2AlNb based alloys by plasma surface alloying[J]. Surface Engineering, 2008, 24(6): 464-469.
[4] WANG Yuanhong, LIU Zhanguo, OUYANG Jiahu, et al. Preparation and high temperature oxidation resistance of microarc oxidation ceramic coatings formed on Ti2AlNb alloy[J]. Applied Surface Science, 2012, 258(22): 8946-8952.
[5] MALECKA J. Investigation of the oxidation behavior of orthorhombic Ti2AlNb alloy[J]. Journal of Materials Engineering and Performance, 2015, 24(5): 1834-1840.
[6] LIU G, WU Y, ZHAO J, et al. Formability determination of titanium alloy tube for high pressure pneumatic forming at elevated temperature[J]. Procedia Engineering, 2014, 81: 2243-2248.
[7] TABATABAEI S M R, SAFARI M, ESFAHANI R S, et al. Experimental and numerical investigation of cold bulge forming of titanium alloy Ti55[J]. World Journal of Mechanics, 2013,3(9):323-327.
[8] LIU Jingyuan, ZHANG Kaifeng. Resistance heating superplastic forming and influence of current on deformation mechanism of TA15 titanium alloy[J]. The International Journal of Advanced Manufacturing Technology, 2015, 76(9): 1673-1680.
[9] BRUSCHI S, ALTAN T, BANABIC D, et al. Testing and modelling of material behavior and formability in sheet metal forming[J]. CIRP Annals-Manufacturing Technology, 2014, 63(2): 727-749.
[10]张久文,陈国清,周文龙,等. 热轧态Ti2AlNb 合金超塑性变形行为的研究[J]. 航空制造技术,2007(增刊):449-453.
[11]周伟, 姚泽坤, 秦春. 工艺参数对粗晶Ti2AlNb合金超塑性行为的影响[J]. 稀有金属材料与工程, 2014(1): 209-213.
[12]ENIKEEV F U, KRUGLOV A A. An analysis of the superplastic forming of a thin circular diaphragm[J]. International journal of mechanical sciences, 1995, 37(5): 473-483.
[13]MIRACLE D B, TAMIRISAKANDALA S, BHAT R B, et al. Titanium alloy microstructural refinement method and high temperature-high strain rate superplastic forming of titanium alloys: U.S. Patent Application 13/344, 818[P]. 2012-1-6.
[14]刘胜京, 徐永超, 姜波, 等. 基于椭球曲面的超塑自由胀形力学解析[J]. 机械工程学报, 2014, 50(18)73-81.
[15]蒋少松, 张凯锋, 吴海峰, 等. 变摩擦控制厚度分布的 TC4 深筒形件正反向超塑成形[J]. 航空材料学报, 2008, 28(6): 16-22.
[16]张雪敏, 曹福洋, 岳红彦, 等. TC11 钛合金热变形本构方程的建立[J]. 稀有金属材料与工程, 2013, 42(5): 937-941.
[17]潘晓华. Ti-6Al-4V 合金等温压缩变形时的温度敏感性指数[J]. 热加工工艺, 2012, 41(14): 89-93.
(编辑王小唯苗秀芝)
The influence of temperature for thickness distribution of Ti2AlNb alloy sheet formed by superplastic free bulging
MA Junlin, LIU Yusheng, LI Ping, XUE Kemin
(School of Material Science and Engineering, Hefei University of Technology, 230009 Hefei, China)
Abstract:In order to research the thickness distribution laws of Ti2AlNb alloy when it is deformed with the superplastic free bulging in high temperature, the Ti2AlNb sheet with an uniform initial thickness, has been studied by the finite element simulation and experiment in this paper. Laws of the limit bulged samples are experimented in the 910 ℃, 930 ℃, 950 ℃ and 970 ℃. And the thickness distribution of finally bulged samples are simulated numerically with the constant strain rate. It is found that, the spherical thickness distribution is uneven after bulging; and Ti2AlNb sheet is bulged into irregular spherical easily; and the temperature relatively effects the spherical shape and the thickness as well. The temperature can affect the thickness distribution of Ti2AlNb alloy sheet formed by superplastic free bulging, based on which the temperature sensitivity index n is considered to correct the E-K model which predicts the thickness of the bulged sheet. The study provides a reference basis for the superplastic deformation of complex thin-walled structures in aerospace of Ti2AlNb alloy.
Keywords:superplastic free bulging; Ti2AlNb alloy; thickness distribution; temperature; FEM
中图分类号:TG306
文献标志码:A
文章编号:0367-6234(2016)05-0172-06
通信作者:李萍,li_ping@hfut.edu.cn.
作者简介:马俊林(1990—),男,硕士研究生;薛克敏(1963—),男,教授,博士生导师.
基金项目:国家自然科学基金资助项目(51175137); 教育部新世纪优秀人才支持计划(NCET-13-0765).
收稿日期:2015-05-08.
doi:10.11918/j.issn.0367-6234.2016.05.028
李萍(1973—),女,教授,博士生导师;

