雷诺数对大跨屋盖结构表面风压的影响
张 建,李 天,杨庆山
(1.北京交通大学 土木建筑工程学院,100044 北京;2.结构风工程与城市风环境北京市重点实验室,100044 北京)
雷诺数对大跨屋盖结构表面风压的影响
张建1,2,李天1,2,杨庆山1,2
(1.北京交通大学 土木建筑工程学院,100044 北京;2.结构风工程与城市风环境北京市重点实验室,100044 北京)
摘要:为研究不同雷诺数对大跨度屋盖结构表面风压分布特性的影响,采用大涡模拟计算流体动力学方法,计算二维屋盖表面平均和脉动风压系数;系统分析雷诺数对屋盖表面风压分布、流动分离及再附着现象的影响.数值计算结果表明:随着屋盖表面特征雷诺数的变化,屋盖表面风压分布亦发生明显变化,特征雷诺数较低时屋盖表面风压较平稳,特征雷诺数升高时屋盖前部的风压系数大幅增大,但增幅逐渐降低,最终趋于稳定.结果验证了雷诺数效应在屋盖结构风荷载模拟中的重要影响.关键词: 大跨屋盖结构;雷诺数效应;计算流体动力学;平均风压系数;脉动风压系数
受到建筑物阻碍作用的影响,建筑附近的气体流动现象十分复杂.当气流冲击到建筑表面时,在其迎风面形成冲击域;随后气流绕过建筑结构向各个方向运动,其中当气流越过迎风面到达建筑屋顶时,沿高度方向产生分离;从屋顶的角部或最高点开始,在屋顶上方产生一个旋涡,其内部缓慢旋转的空气气团形成闭合分离泡.随着来流的变化,建筑结构附近的特征流场亦随之变化,造成建筑结构表面风荷载分布的改变,特别是对于建筑结构的气流分离区、边界和转角的位置,风荷载分布变化程度最剧烈[1-2].
基于上述分析可知,大跨度屋盖表面复杂风压分布不但受到屋盖几何外形的影响还会随着来流条件的变化而变化[3-6].目前对于屋盖结构风压特性的研究方法多采用风洞实验和数值计算方法[7-8].数值模拟方法可精确计算屋盖表面的平均与脉动风压分布,分析不同来流条件下屋盖附近的流动状态,进而获得屋盖表面的压力分布[9-14].本文以二维平屋盖为例,采用大涡模拟方法,进行大跨度屋盖结构的绕流数值模拟,研究不同雷诺数条件下,不同特征来流对屋盖表面风压分布的影响,为后续柔性屋盖结构风致流固耦合效应研究做铺垫.
1数值模型
1.1控制方程
常用的湍流模拟方法包括雷诺时均法和大涡模拟法.相比雷诺时均法,大涡模拟建立在湍流统计理论和拟序结构认识的基础上,因而其对小尺度的流动模拟更为精确,更适用于脉动压力场的分析,所以本文采用大涡模拟方法对屋盖的平均风压和脉动风压分布进行计算.对Navier-Stokes方程在波数空间或者物理空间进行过滤,得到大涡旋的控制方程[15]:
(1)
(2)
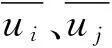
本文采用Smagorinsky-Lilly亚格子模型来表示亚格子雷诺应力,其表达式为
(3)
式中μt是亚格子尺度的湍动粘度,其表达式为
(4)

(5)
式中:K是Karman常数,d是计算单元到壁面的最近距离,V是计算单元的体积,Cs是Smagorinsky常数,根据亚格子应力的耗散性取为0.10.
1.2计算模型
计算模型为一个四周封闭的平屋盖结构(图1),尺寸为L×H=50cm×10cm,宽高比为L/H=5.模型置于250cm×100cm的计算域中,模型前缘距离入口80cm.网格采用四边形结构网格,共约有20万网格(710×280),其中壁面网格厚度为2mm,沿高度方向和沿流向的网格尺寸变化率均为1.05(图2).

图1 计算区域(dm)

图2 网格划分
来流只考虑平均风成分,其剖面表达式为u=u0(z/z0)α,α=0.12;参考高度z0=10cm;u0为参考高度处的平均风速.雷诺数的定义为[7]
(6)
式中:空气密度ρ=1.225 kg/m3,空气动气粘度μ=1.789 4×10-5kg/(m·s).通过调整参考高度处的平均风速u0来改变雷诺数,进而描述不同特征来流条件.
出口边界处采用完全发展出流条件,即出口处所有物理量垂直于出口方向的法向梯度等于零;计算域顶边采用滑移壁面条件;地面和建筑结构表面为无滑移壁面条件(见表1).

表1 边界条件
计算差分格式为二阶中心差分.由于计算初始压强场赋零值,计算初始阶段流场会出现波动,为了保证得到稳定的压力场并分析屋盖旋涡运动的完整过程,计算时长取80 s,时间步长取0.001,内迭代步为20.
2计算结果分析
考虑不同雷诺数下的平屋盖表面风压分布特性的数值模拟,首先通过记录屋盖上若干测点(图3)的风压时程,分析计算时长的影响;将数值计算结果与对应结果[16]进行比较,验证计算方案的精度;最后对比不同雷诺数下的风压特性,分析不同特征来流对屋盖表面风压分布,进而分析屋盖附近的旋涡演变规律.
2.1计算时长对结果的影响
如图3所示,在屋盖表面沿顺风向选取a、b、c、d和e等5个监测点,其距离屋盖前沿的距离分别为0.1L、0.3L、0.5L、0.7L和0.9L(L为屋盖跨度),用来监测流场变化对风压的影响.图4、5分别给出雷诺数1 000与3 000条件下,计算时间内监测点的风压时程,分别代表低雷诺数与高雷诺数条件下的变化特性.

图3 屋盖表面监测点

图4 风压时程(Re=1 000)

图5 风压时程(Re=3 000)
如图4所示,当雷诺数为1 000时,屋盖表面风压波动幅度较小、频率较低,沿流向波动幅度增大.流场初始阶段的波动相对于低雷诺数下的流场不可忽略,会影响屋盖风压计算结果.但当雷诺数为3 000时(图5),屋盖风压本身波动幅度大频率高,受初始化影响较小.为进一步说明流场初始波动的影响,对于不同雷诺数,分别取不同计算时段计算屋盖表面平均风压与脉动风压,计算结果见图6、7.

图6 风压系数(Re=1 000)

图7 风压系数(Re=3 000)
可以看出,当风压计算统计流场初始波动阶段时,对于低雷诺数条件,计算得到的平均风压与脉动风压峰值偏大,且分布规律与稳定阶段的计算结果不同,峰值点前移;对于高雷诺数条件,是否统计流场初始波动阶段影响较小.因此,根据雷诺数的不同合理选取流场稳定时段进行风压统计计算,有利于得到准确结果.为了保证计算结果不受初始化流场波动的影响,本文算例统一选取20~70 s时段进行风压计算.
2.2对比验证
考虑20~70 s内的屋盖表面风压分布,计算文献[16]中的算例(Re=10 000)验证本文方法.如图8所示,通过比较发现,两者得到的屋盖表面风压分布趋势基本一致,风压数值有一些偏差,究其原因,一方面因为采用了不同的湍流模型,另一方面也可能是因为本文采用的LES方法与文献[16]采用的RSM模型计算精度不同,使结果有一定偏差.因此可以说本文的数值模拟结果能得到与文献结果基本一致的风压分布,具有相当的可信度,可用于结构静力风荷载的分析研究.

图8 本文数值模拟结果与文献[16]数值模拟结果对比
2.3不同雷诺数下的风压特性
图9、10给出了不同雷诺数下屋盖表面平均风压与脉动风压的计算结果.屋盖表面的平均风压峰值与脉动风压峰值一一对应,通过风压分布可以描述屋盖表面的旋涡运动情况,并预测雷诺数继续增大后风压分布的变化情况,主要包括以下几点:

图9 不同雷诺数下的平均风压
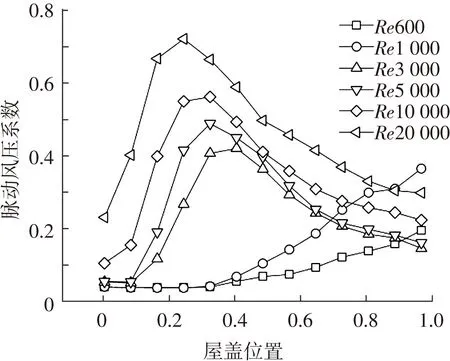
图10 不同雷诺数下的脉动风压
1)屋盖表面的风压分布形态与扰流模式在低雷诺数和高雷诺数条件下有明显区别.对于高雷诺数(Re≥3 000),屋盖前缘负压急剧下降达到极大值,同时脉动风压也达到最大值,这说明在此处产生流动分离,并在屋盖上部形成旋涡,引起强风吸力;随后负压减小,到屋盖中部达到极小值,说明在此处发生流动再附着;最后在屋盖后缘负压再次增大趋势,同时脉动风压也急剧上升,说明在此处再次产生流动分离.
2)对于低雷诺数(Re≤1 000),屋盖前缘产生流动分离,产生风吸力,但是没有较强的旋涡形成,因此平均风压比较平稳,脉动风压很小;在屋盖后部负风压达到极小值,说明此处发生再附现象,同时脉动风压达到极大值,是因为低雷诺数下再附引起的波动性相对于旋涡本身更强;在屋盖后缘发生与高雷诺数相同的流动再次分离现象.
3)对于雷诺数1 000~3 000过渡阶段,风压分布可以根据计算结果推断出大致的趋势,平均风压与脉动风压分布介乎高雷诺数与低雷诺数之间,其峰值点在此期间随雷诺数增大向屋盖前缘移动.
4)对于相同的分布形态,随着雷诺数的改变,平均风压的峰值基本保持不变,而脉动风压的峰值随雷诺数增大逐渐提高.如在高雷诺数条件下,在本文所计算的3 000≤Re≤20 000区间内,随雷诺数增大平均风压增幅约为3%,而脉动风压增幅达到约80%.同时,随雷诺数增大风压分布的变化率逐渐减小,由此可推断出,当雷诺数增大到一定程度,在附着点不会继续移动,屋盖表面形成较为稳定的风压分布,甚至不再受到雷诺数变化的影响.
3结论
1)采用大涡模拟方法进行钝体结构准定常绕流流场研究时,需考虑流场初始化的影响,特别对低雷诺数流动问题,初场会导致风压异常波动,因此,根据流场雷诺数的不同合理选取流场稳定时段进行风压统计计算,才可得到准确结果.
2)随着雷诺数的提高,屋盖表面流场发生较大变化,分离区与再附区的位置均随着雷诺数的变化而变化,因此雷诺数引起的特征流动对屋盖风压分布具有重大影响.
3)待流场稳定后,虽然屋盖表面的平均风压分布形态基本相似,不再受来流雷诺数的影响;然而脉动风压分布仍然随雷诺数的增大而变化,因此对于对脉动风压敏感的柔性屋盖结构,需要重点考虑雷诺数效应的影响.
参考文献
[1] 张建. 采用修正来流条件和粗糙壁面处理方法的绕流问题研究[D].北京:北京交通大学,2011.
[2] 谢壮宁, 倪振华, 石碧青. 大跨屋盖风荷载特性的风洞试验研究[J]. 建筑结构学报,2001,2:23-28.
[3] 顾明, 王新荣. 工程结构雷诺数效应的研究进展[J]. 同济大学学报, 2013, 41(7): 961-969.
[4] LAROSE G L, D’AUTEUIL A. On the Reynolds number sensitivity of the aerodynamics of bluff bodies with sharp edges[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2006,94(5): 365-376.
[5] SCHEWE G. Reynolds-number effects in flow around more-or-less bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2001, 89(14/15): 1267-1289.
[6] ROBERTSON J M, CERMAK J E, NAYAK S K. A Reynolds-number effect in flow past prismatic bodies[J]. Mechanics Research Communications,1975(5/6): 279-282.
[7] 张建, 杨庆山. 基于标准k-ε模型的平衡大气边界层模拟[J]. 空气动力学学报, 2009(6):729-735.
[8] 朱伟亮. 基于大涡模拟的CFD入口条件及脉动风压模拟研究[D]. 北京:北京交通大学, 2011.
[9] 杨庆山, 王基盛, 朱伟亮. 薄膜结构与空气环境静力耦合作用的试验研究[J]. 土木工程学报,2008(5):19-25.
[10]ALRAWASHDEH H, STATHOPOULOS T. Wind pressures on large roofs of low buildings and wind codes and standards[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2015, 147: 212-225.
[11]FU J Y, ZHENG Q X, WU J R, et al. Full-scale tests of wind effects on a long span roof structure [J]. Earthquake Engineering and Engineering Vibration, 2015, 14(2): 361-372.
[12]KAWAI H. Structure of conical vortices related with suction fluctuation on a flat roof in oblique smooth and turbulent flows[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71:579-588.
[13]RIZZO F. Wind tunnel tests on hyperbolic paraboloid roofs with elliptical plane shapes[J]. Engineering Structures, 2012, 45: 536-558
[14]ZHOU Z, LI Z M, MENG S P,et al. Wind-induced vibration responses of prestressed double-layered spherical latticed shells[J]. International Journal of Steel Structures, 2011, 11(2): 191-202.
[15]埃米尔.希缪. 风对结构的作用——风工程导论[M]. 上海:同济大学出版社, 1992.
[16]武岳.考虑流固耦合作用的索膜结构风致动力响应研究[D].哈尔滨:哈尔滨工业大学,2003.
(编辑赵丽莹)
Reynolds number effectson wind pressure distribution of large-span roof structure
ZHANG Jian1,2, LI Tian1,2,YANG Qingshan1,2
(1.School of Civil Engineering, Beijing Jiaotong University,100044 Beijing, China;2.Beijing’s Key Laboratory of Structural Wind Engineering and Urban Wind Environment, 100044 Beijing, China)
Abstract:Reynolds numbers have great effects on the pressure distribution of large-span roof structure. To explore these issues, Large Eddy Simulation (LES) numerical method was adopted to calculate mean and fluctuation wind pressure distributions. The pressure values, flow separation and reattachment patterns were examined by corresponding experiment data. Results indicate that the pressure distribution changed dramatically with different Reynolds numbers. Pressure distribution keep srelatively stable in low Reynolds number flow field, while for high Reynolds number flow,pressure varies rapidly at the leading edge area of the roof and gradually decreases to a constant value. The simulation results prove that Reynolds numbers have critical effects on the pressure distribution of the large-span roof structures.
Keywords:large-span roof structure; Reynolds number effect; computation fluid dynamics; mean wind pressure coefficient; fluctuation wind pressure coefficient
中图分类号:TU312
文献标志码:A
文章编号:0367-6234(2016)06-0038-05
通信作者:张建, zhangjian@bjtu.edu.cn.
作者简介:张建(1981—),男,讲师;杨庆山(1968—),男,教授,博士生导师.
基金项目:国家自然科学基金 (51578059);
收稿日期:2015-02-12.
doi:10.11918/j.issn.0367-6234.2016.06.006
中央高校基本科研业务费(2015JBM074).

