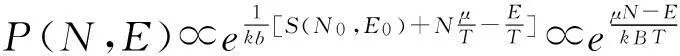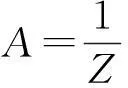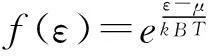关于近独立子统计分布导出的探讨

李建英

(忻州师范学院，山西忻州 034000)



关于近独立子统计分布导出的探讨

李建英

(忻州师范学院，山西忻州 034000)

[摘要]本文采用Darwin-Fowler平均法和Gibbs统计系综理论，由熵和巨正则分布分别导出近独立子的三种统计分布，克服了Boltzmann概率法在数学上人为假设的缺点，为三种统计分布的正确性提供了坚实的理论基础。

[关键词]玻色-爱因斯坦分布；费米-狄拉克分布；麦克斯韦-玻耳兹曼分布

任一宏观量都是在一定宏观条件下所有可能达到的微观运动状态的相应微观量的统计平均值，在这一观点的前提下，有不同的求统计平均值的方法，如Boltzmann的概率法、Darwin-Fowler的平均法、Gibbs的统计系综理论.对于近独立子的三种统计分布律导出，绝大部分教材采用Boltzmann的概率法，在导出过程中都假设ωi>>1，ni>>1，并使用了Stirling近似公式，实际上所作的假设未必能满足，因此这是严重的缺陷，采用Darwin-Fowler的平均法和Gibbs的统计系综理论导出所述的分布律则不存在数学上人为假设的缺点，为它们的正确性提供了坚实的理论基础.

1用Gibbs的统计系综理论，由巨正则分布导出近独立子的三种统计分布

考虑全同近独立子体系的巨正则系综，其布函数为

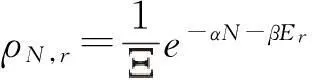
配分函数为

1.1Boss-Einstein分布律

玻色子的能级分布{ni}的总量子状态数为

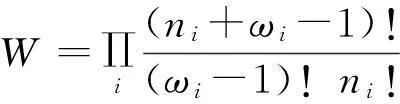
配分函数为

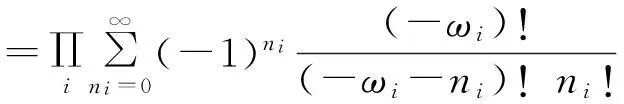
能级εi上的平均粒子数为

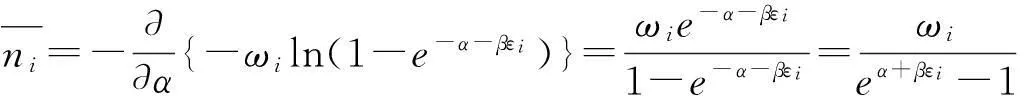
1.2Fermi-Dirac分布律

费米子遵守Pauli原理，ωi≥ni，能级分布{ni}的总量子状态数为

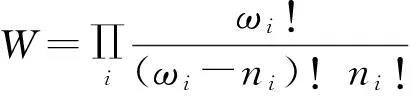
巨正则配分函数为

能级εi上的平均粒子数为

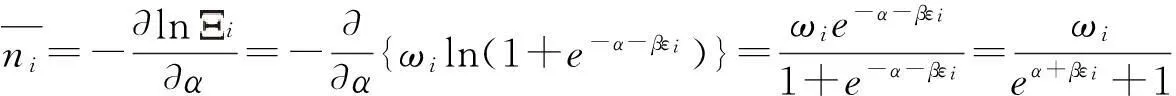
1.3Maxwell-Boltzmann分布律

离域独立子经典体系，能级分布{ni}的总量子状态数为

巨正则配分函数为

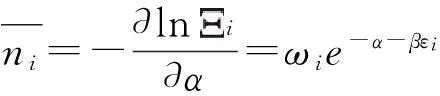
2用Darwin-Fowler的平均法，由熵引出三种统计分布

考虑一个具有恒定能量E0与恒定粒子数N0的很大的孤立系统，它由系统与其余很大的称为媒质的部分构成，系统与媒质可以交换能量与粒子.当系统的能量为E，粒子数为N时，媒质的能量则为E0-E，粒子数为N0-N.当系统与媒质处于热平衡时，两者的温度T与化学势μ相等.

设系统对应于能量E的状态数为WE，为一小量，因此系统与媒质所拥有的状态数近似为媒质所拥有的状态数，W(N0-N，E0-E)，系统有N个粒子，能量为E的概率也就是媒质有N0-N个粒子，能量为E0-E的概率，这个概率和状态数W(N0-N，E0-E)成正比，即P(N，E)∝W(N0-N，E0-E).

现用媒质的熵表示，则有

S(N0-N，E0-E)=kBlnW(N0-N，E0-E).

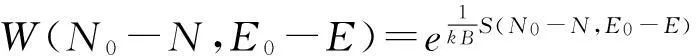
设N<

所以

若系统的能级E对应的状态数WE≠1，则有

2.1Fermi-Dirac分布

现考虑由N个费米子构成的孤立系统，总能量为E，它由一个小系统与大媒质组成，取1个或0个费米子占据的单个量子态作为系统，取N个或N-1个费米子占据的其它量子态作为媒质.系统与媒质可以交换一个粒子和能量ε.由于费米子服从泡利原理，所以，对应的媒质所拥有的状态数为W(N，E)或W(N-1，E-ε).熵为S(N，E)=kBlnW(N，E)或kBlnW(N-1，E-ε).

设系统的能量ε对应的状态数WE=1，则系统有n个费米子，能量为nε的概率为

P(n，nε)∝W(N-n，E-nε).

或

2.2Boss-Einstein分布

现考虑玻色子系统，方法与费米子系统相同，差别在于对于费米子系统，n=0，1，而对玻色子系统，由于不受泡利原理制约，能量为ε的单个量子态允许有任意个玻色子占据，n=0，1，2，….

设系统的能量ε对应的状态数WE=1，则系统有n个玻色子，能量为nε的概率为

P(n，nε)∝W(N-n，E-nε).

或

2.3Maxwell-Boltzmann分布—经典情况

这是费米分布与玻色分布的共同极限情况，这就是经典的玻耳兹曼分布.

3讨论

(1)用Darwin-Fowler的平均法，在数学方法上比概率法严格；另外，由熵引出三种统计分布，更突出了熵概念在统计物理中的重要地位，是对熵概念的进一步深化.

(2)Gibbs的统计系综理论，由巨正则分布导出近独立子的三种统计分布，数学严谨，物理概念清晰，对独立子体系与相依子体系都适用，是平衡态统计理论最完美的方法.

[参考文献]

[1]高执棣,郭国霖.统计热力学导论[M].北京:北京大学出版社,2004.

[2]汪志诚.热力学·统计物理[M].北京:高等教育出版社,2003.

[3]严燕来,叶庆好.大学物理拓展与应用[M].北京:高等教育出版社,2002.

[4]梁希侠,班士良.统计热力学[M].呼和浩特:内蒙古大学出版社,2000.

A Study on Derivating the Statistical Dstribution of Approximately Independent Partical

LI Jian-ying

(Xinzhou Teachers University, Xinzhou Shanxi 034000, China)

Abstract:In the artical,statistical distributions of the appximately independent partical are derivated from entropy and grand canonical distribution through Darwin-Fowler statistical average and Gibbs statistical ensemble theory. It overcomes the shortcomings of Boltzmann probability statistics that gives the man-made assumption in mathematics and provids the solid theoretical basis for the correctness of three statistical distributions.

Key words:Boss-Einstein distributions; Fermi-Dirac distributions; Maxwell-Boltzmann distributions

[中图分类号]O21

[文献标识码]A

[文章编号]2095-7602(2016)04-0008-04

[作者简介]李建英(1967- )，女，副教授，硕士，从事热力学、统计物理和基础物理实验教学研究。

[基金项目]忻州师范学院基金项目“地方师范院校物理学专业实验教学体系构建和创新人才培养模式研究”(JGZD201511)。

[收稿日期]2015-12-30