Experimental Evaluation on a Newly Developed Dynamic Positioning Time Domain Simulation Program

(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;School of Naval Architecture,Civil and Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Experimental Evaluation on a Newly Developed Dynamic Positioning Time Domain Simulation Program

XÜ Sheng-wen,WANG Lei,WANG Xue-feng,LI Bo

(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China; Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration(CISSE),Shanghai 200240,China;School of Naval Architecture,Civil and Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Numerical and experimental evaluation methods including static capability analysis,time domain simulation and model test should be used to design,analyze and predict the performance of a dynamic positioning system(DPS)before commissioning it.To validate the performance of the DPS in an accurate and economic way,a new software program which is able to conduct an‘experiment’to evaluate a newly designed dynamic positioning system and its subsystem was developed in the MatlabSimulink environment.And,the reliability of the newly developed Dynamic Positioning Time Domain Simulation Program,DPTDSP was evaluated by a simplified model test on a semi-submersible.The results show that the program could be used as a marine research tool to investigate the performance of the newly designed DPS or new modules of the system.

DPS;DPTDSP;time domain simulation;marine research tool

0 Introduction

Dynamic positioning system(DPS)has been widely used in offshore engineering over the last five decades.A dynamically positioned(DP)vessel is by the International Maritime Organization(IMO)and the certifying class societies(DNV,ABS,LR,etc.)defined as a vessel that maintains its position and heading(fixed position or pre-determined track)exclusively by means of active thrusters.Dynamic positioning system mainly consists of four primary sub-systems:the power generation and distribution system,the control system,the sensor system and the thrust system,as described in Sørenson(2011)[1].The power generation and the distribution system comprises all units necessary to supply the DP system with power.The control system generally includes the main control unit which generates the required thrust forces with the optimal thruster allocation unit.The sensor system provides the position and heading infor-mation of the vessel to the control system.The sensor system is composed of the position reference unit,gyros,wind sensors and the relevant hardware and software.The thrust system involves all components necessary to supply the DPS with thrust forces.

Over the last five decades,dynamic positioning in deep water has been used in the marine sector,oil and gas industries,military services in many tasks such as drilling,oil and gas floating production platforms,cable and pipe laying,docking and towing,side by side arrangement of FPSO and shuttle tanker,see Mahfouz and El-Tahan(2006)[2].Each of these operations benefits from a DPS’s ability to include precise position-keeping,freedom from the restrictions of mooring spread systems,the ability to move quickly from one site to another,applies easily to any depth of water and track-keeping capabilities.

Numerical and experimental evaluation methods including static capability analysis,time domain simulation and model test should be used to design,analyze and predict the performance of a newly designed DPS before commissioning it.The static dynamic positioning capability analysis generally provides a primary investigation of the DPS.Model test in an ocean basin is a reliable or the best way to evaluate the DPS.However,the model test is always constrained by the significant consumption of time and money.Time domain simulation may be an alternative tool for design,analysis and predication of the DPS under these circumstances.

The main objective of this paper is to propose a newly developed software program which is able to conduct an‘experiment’to evaluate a newly designed dynamic positioning system in the MatlabSimulink environment.In addition,the reliability of the developed Dynamic Positioning Time Domain Simulation Program,DPTDSP was validated by a simplified model test on a semi-submersible.

This paper is logically constructed in six chapters.Chap.1 contains the mathematical modeling of DP vessels.In Chap.2 the developed Dynamic Positioning Time Domain Simulation Program,DPTDSP is presented.Chap.3 is about the setup of the experiment.In Chap.4 the comparison between the simulation and experimental results is given.Finally,conclusions are drawn in Chap.5.

1 System modeling

1.1 3 DOF Kinematics

The different coordinate systems used in this paper are illustrated in Fig.1 and described below,see Sørensen and Peter Strand(2000)[3].

·The Global coordinate system also named Earth-fixed coordinate system is denoted as the XGYGZGcoordinate system.

·The vessel-parallel XVYVZVcoordinate system is fixed in the Global coordinate system and rotated to the desired heading angle ψ0.The origin is translated to the desired x and y positions.

·The body-fixed XYZ coordinate system is fixed to the vessel body with the origin located at the mean oscillatory position in the average water plane with(xG,0,zG). The x axis points towards the head of the semi-submersible.

The linear and angular velocity of the vessel in the body-fixed coordinate system relative to the Global coordinate system is given by Eq.(1).

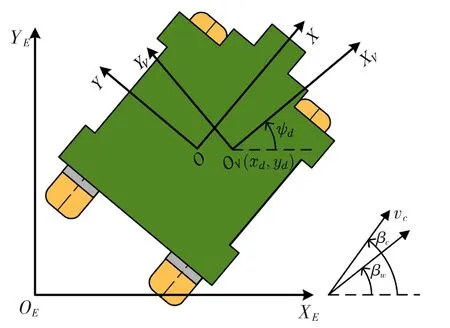
Fig.1 Reference coordinates

The vectors defining the vessel’s Global coordinate position and orientation,and the body-fixed translation and rotation velocities are given by

1.2 Nonlinear low-frequency vessel model

The nonlinear 3 DOF coupled equations of the low frequency motions in surge,sway and yaw are written as follows:

where M is the system inertia matrix including the added mass,which can be found in Faltinsen(1990)[5]for detailed expression.CRB∈R3×3is the skew-symmetric Coriolis and centripetal matrix due to the rotation of the body coordinate system about the inertial earth coordinate system,which can be found in Fossen(2011)[6]for detailed expression.Wichers(1988)[7]divided the effect of current into two parts:the potential part and the viscous part.The potential part is formulated as CAvr（）vraccording to Fossen(2011)[6].Notice that the so-called Munk moments appear from the expression CAvr（）vr.The damping vector may be divided into nonlinear and linear components according to:

For most vessels it is hard to calculate the damping coefficients.A combination of empirical formulas,model tests and computational fluid dynamics(CFD)are normally used to find the damping coefficients.The detail formulation of D vr（）can be found in Sørensen and Ronxssis the restoring vector which is a zero vector here considering the horizontalplane model.

The right-hand expression of Eq.(5)represents generalized external forces on the vessel. Forces in surge and sway and moment in yaw are referred to as the generalized forces.τenv∈R3represents the slowly varying environmental loads with the exception of current loads acting on the vessel(i.e.the wind loads and the second order mean and low frequency wave loads). The effect of current is already included on the left-hand side of Eq.(5)by the introduction of the relative velocity vector.If the vessel is attached to a mooring system,the effect of this is represented by τmoor∈R3.τ represents the generalized forces generated by the propulsion system.

The wind loads on a marine vessel are proportional to the projected area above the waterline and square of the wind speed.The components of the wind velocities are defined according to:

where Vwand βware the wind velocity and direction,respectively(see Fig.1).ψ is the heading of the vessel in the Global coordinate system.The wind velocity assumed to be much larger than the vessel velocity,such that the wind load vector is formulated:

where ρais the density of air;Loais the overall length of the vessel.Lxzand Lyzare the vertical distances between transverse and longitudinal origin and the wind load point of attack.Axand Ayare the lateral and longitudinal areas of the non-submerged part of the vessel projected on the yz-plane and xz-plane.Cwx,Cwyand Cwψare the non-dimensional wind coefficients in surge,sway,and yaw,respectively.These coefficients are often found by model test or by employing formulas as presented in Isherwood(1973)[9].In addition,CFD method can also be implemented to evaluate the wind loads,see Gosman(1999)[10]and Zhang et al(2010)[11].

The second order wave forces are often divided into three components:mean drift forces, low(difference)frequency forces and high(sum)frequency forces.The mean and low frequency forces contribute a significant part of the total excitation forces in the low-frequency model.However,for the applications considered here,the effect of the rapidly varying high frequency forces can be neglected.The determination of the second order mean and low frequency wave forces can be done by means of quadratic transfer functions,as described in Faltinsen (1990)[5]and Newman(1977)[12]:

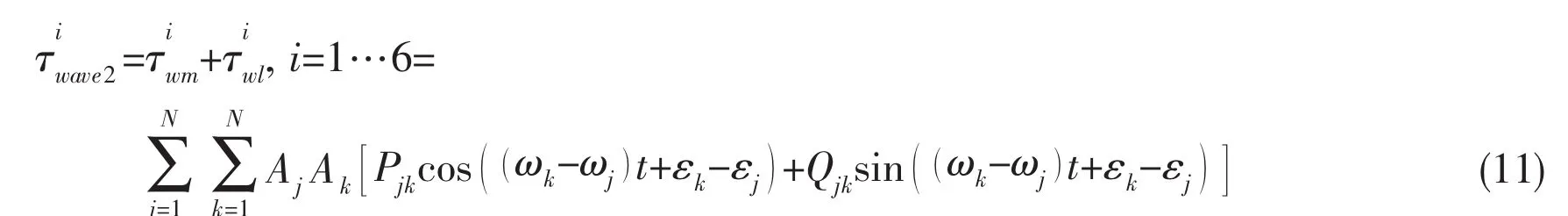
where ωjis the wave frequency;Ajis the wave amplitude and εjis a random phase angle.The quadratic transfer operators Pjkand Qjkare dependent on both first and second order velocity potentials,which can be obtained from potential software program.

The generalized forces generated by the propulsion system can be expressed as:

The vector u∈Rmcontains the magnitudes of the force produced by each individual actuator.The angle αiis the azimuth angle of the i-th actuator,defining the direction of the force produced in the vessel body-fixed coordinate system.The is-th column of the 3×m matrixis given by

The location of the i-th actuator in the vessel isin the body-fixed coordinate system.

1.3 Linear wave-frequency model

1.4 Controller

A nonlinear horizontal plane positioning feedback controller of PID type is formulated as:

where,e∈R3is the position and heading deviation vector,is the velocity deviation vector,and z∈R3is the integrator states defined as:

ψd∈R3is the vector defining the desired position and heading angles in the Earth-fixed coordinate system.Kp,Kd,Ki∈R3×3are the non-negative controller gain matrices found by appropriate controller synthesis method or trial-and-error method in some complex cases.

1.5 Observer

A nonlinear passive observer proposed by Fossen and Strand(1999)[13]is adopted here as a low pass filter.The DP observer model is formulated as follows:

where Eq.(20)is a vector form of Eq.(14).Eq.(21)represents the state space model of the wave frequency motions.The first order Markov model is applied for simulating the low frequency environmental loads in Eq.(22).w1,w2and w3are white noises.

1.6 Thruster allocation

Thrust allocation problem can be formulated as optimization problems,where the objective is typically to minimize the use of the control power and the gap between the commanded and achieved force subjected to actuator rate and other operational constraints.The commanded forces(moments)come from the corresponding control law.

Johansen et al(2004)[14]proposed a constrained nonlinear control allocation method with singularity avoidance.The method uses sequential quadratic programming,solving at each sample a convex quadratic program approximating the nonlinear program.The following optimization problem is defined.

subjected to

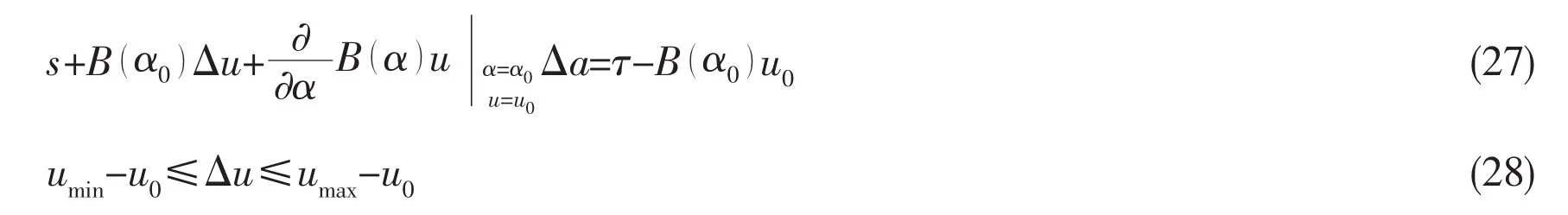
where Wi,uiare the i-th actuator’s consumed power and thrust force,respectively.Δα,Δu are the azimuth actuator’s angle and thrust difference between this sample and the last sample,respectively.The second term sTQs in Eq.(26)penalizes the error between the commanded and achieved force.The maximum and minimum forces by the actuators are specified through the constraints in Eq.(28).The azimuth angles α,are required to be constrained to given sectors defined by the vectors with lower and upper bounds,αminand αmaxin Eq.(29).Moreover,the rate-of-change in azimuths is constrained in Eq.(30)and minimized by the third term in the criterion.Singularity is avoided through the last term in the criterion,where є＞0 is required to avoid numerical problems and ρ＞0 is a weighting parameter.

2 Numerical simulator,DPTDSP

Based on the present study,a time domain simulation program is developed in the MatlabSimulink environment.The main structure of the Dynamic Positioning Time Domain Simulation Program,DPTDSP is illustrated in Fig.2.Actuators can be disabled or enabled during the simulation,thus one can evaluate the positioning performance of DPS under actuator failures.The modules of the program given in Fig.2 are described below.

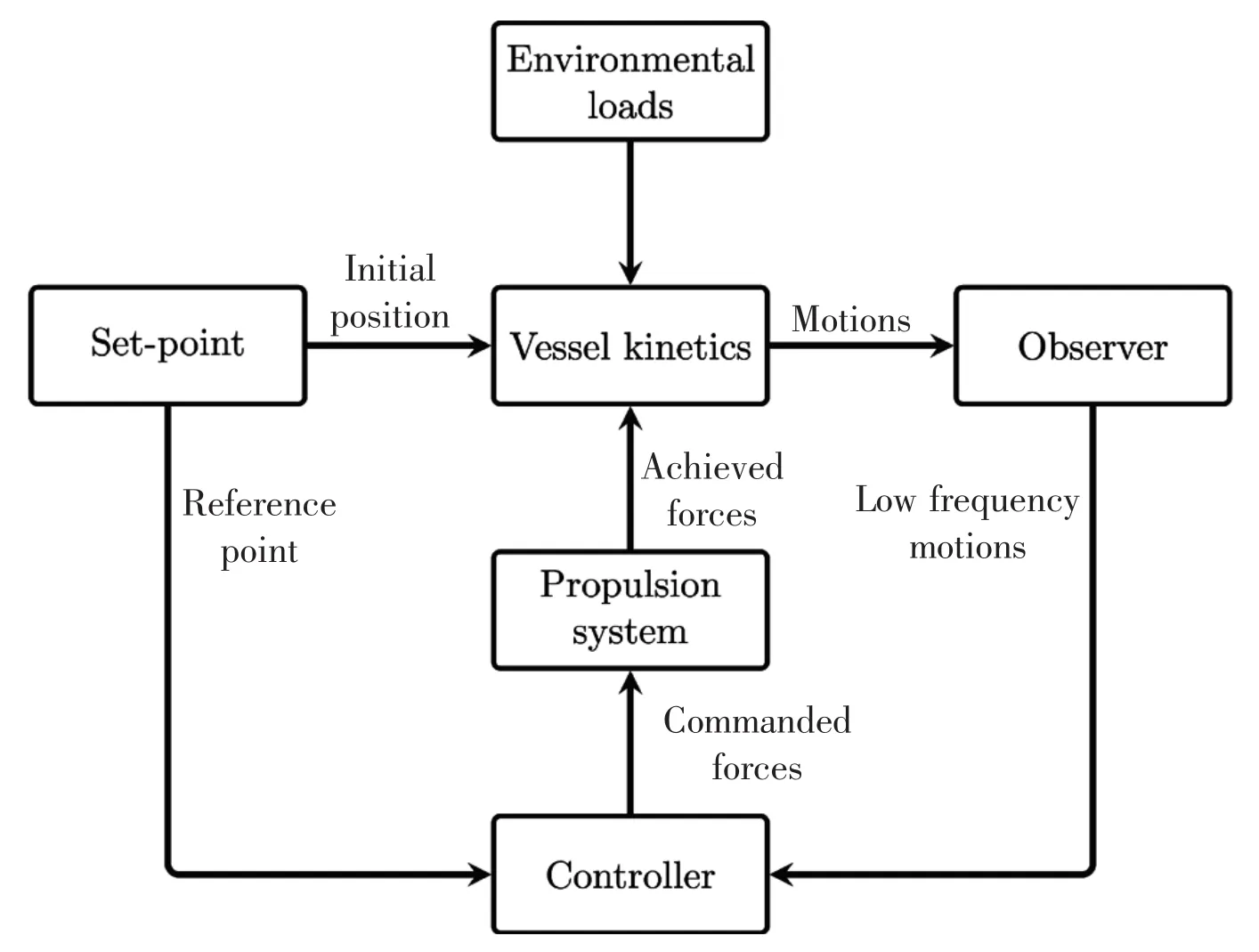
Fig.2 Description of the DPTDSP

·Set-point module

Set-point module is used to set the desired position and heading angle x,y,（ ）ψ for the vessel to be positioned.Initialization of set-point has been done.However,one can modify theset-point before and during the simulation.

·Environment loads module

The wind loads and low frequency second order wave loads are estimated in this module. Wind forces and moment are estimated by CFD method or model test.Low frequency second order wave loads are estimated by means of quadratic transfer functions.The irregular waves are generated in this module given the wave spectrum,significant wave height and peak spectrum periods.

·Vessel kinetics module

The nonlinear low frequency vessel model derived from Chap.1 is implemented here.The input of the vessel kinetics module is the low frequency environmental loads from the environmental loads module,propulsion forces and moment,current velocity and direction.Wave frequency motions are obtained by the transfer functions RAO based on the waves generated in the environmental loads module.The output of the vessel kinetics module is the sum of the low frequency and wave frequency motions and velocities.

·Observer module

The nonlinear passive wave filter is employed to separate the high frequency components from measurement signals obtained from the vessel kinetics module.Such a decomposition must be performed since the DPTDSP controller module must only take the low-frequency motion into consideration.Suppressing high frequency motion requires enormous power to be attenuated and can cause extra tear and wear on actuators.

·Controller module

The controller uses the low frequency motions obtained from the observer module to calculate the commanded forces and moment which should be provided by the propulsion module.A wind feed forward‘enable/disable’option can be checked.Control parameters can be defined here during the simulation.

·Propulsion module

Propulsion module is required to provide the commanded forces and moment against the environmental forces.Thrust allocation must be used to allocate commanded forces and moment among the whole thrust system.The thrust allocation guarantees minimum power consumption based on the premise that the thrust system generates the required forces and moment.

3 Experimental set-up

In order to validate the DPTDSP,an experiment was implemented in the deep ocean basin of the State Key Laboratory of Ocean Engineering,SKLOE,SJTU.The basin size is 6 m deep, 30 m wide and 50 m long.Wind,current,and wave were generated in the unique direction. In the experiment,a semi-submersible with eight azimuth thrusters was adopted,with a scale factor λ=50.Parameters of the semi-submersible are tabulated in Tab.1.The coordinate systems adopted in the experiment is the same as given in Fig.1.Thruster configurations are giv-en in Fig.3.

Tab.1 Parameters of the semi-submersible

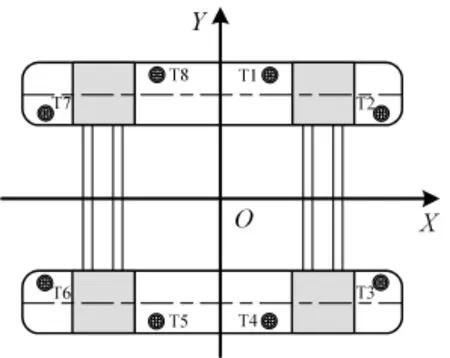
Fig.3 Thruster configuration of the semisubmersible

Fig.4 Ka 4-70 thruster and No.19A tunnel model

Ka 4-70 thruster and No.19A tunnel model designed by SKLOE is shown in Fig. 4 and curves of Kt,Kqand η obtained from model test are illustrated in Fig.5.The full scale tunnel thruster has the similar open water performance with the tested model.

An illustration of the experimental setup is given in Fig.6.The experimental results are transformed to full scale by requiring that the Froude numberis constant.

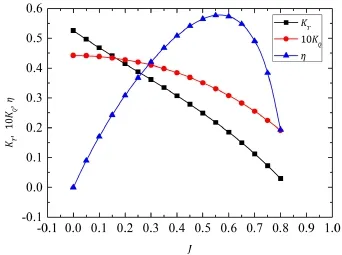
Fig.5 Open water performance of Ka 4-70 thruster and No.19A tunnel model

The environmental condition in the experiment is determined as the scaled operation condition(see Tab.2)of the semi-submersible in South China Sea.JONSWAP wave spectrum was adopted in the experiment.

Tab.2 Environmental conditions in experiment and simulation

Fig.6 Illustration of the experimental set-up

The wind was generated by a conventional fan.The wind velocity was calibrated with an anemoscope.The current was generated by means of water pumps in a re-circulation duct, moving the water from one side of the basin to another.Prior to the wave adjustment,the current speed was adjusted.For the generation of waves,the controlled flap type wave makers are oscillated with varying velocity and stroke.The requested wave conditions were adjusted prior to the model tests for duration of 3 hours full scale,without model present in the basin.This was done by measurement at the equilibrium position of the positioned semi-submersible without environment.The wave elevation was measured by means of a resistance wire wave probe.

The position and heading angle of the semi-submersible are measured by the data acquisition software called Qualisys Track Manager,QTM,with which the real time 3D and 6D motions can be acquired.Rigid body is defined by five LEDs installed on the semi-submersible.The LEDs are tracked and their positions are acquired by the QTM server.With such information,the software is able to evaluate the position and heading of the semi-submersible.

All numerical calculations are carried out by a Pentium II 1.3 GHz computer,with a timestep of 1 s.A PID controller was adopted to generate the commanded forces and moment. Kalman filter was adopted to filter out the high frequency motions from the motions measured by the QTM.The commands to the electric motor were sent to the semi-submersible model via a motor drive controller.

Tab.3 Investigated cases for thruster failure mode analysis

As there was no anemometer available in the experiment,the wind feed-forward control was not enabled.Fifteen cases were investigated both in the simulation and experiment,as given in Tab.3.Wind,waves and current are coincident in the same direction with β=0.Thruster failure modes were considered in the thruster configuration.

4 Results and discussions

The results in the experiment are scaled to the real dimension of the semi.As the observers used in the simulation and experiment are different,the time traces of the position and heading are not congruous.Even though it is meaningless to compare the time traces,a statistical analysis of the results may be helpful.

Tab.4 Standard deviations of the semi’s motions in numerical simulation and experiment

The results in the simulation and experiment were statistically analyzed to obtain the standard deviations of the semi’s positions and headings,as shown in Tab.4.The surge motion and the drift radius coincide with each other very well for cases C21～C35.The sway and yaw motions in the numerical simulation and experiment coincide very well for cases Case11～C25.However,for cases C11～C15,the surge and yaw motions do not coincide well;for cases C31～C35,the sway and yaw motions do not coincide well,either.This phenomenon may be caused by the lack consideration of noise in the simulation.The noises are very significant in the experiment.Moreover,the waves used in the experiment are not exactly long crested waves. Orthogonal wave forces can not be omitted and they may cause large orthogonal motions. However,in the numerical simulation,since the waves are strictly long crested waves,little force comes from the orthogonal directions for cases C11～C15 and C31～C35,the motions arevery moderate.

The program can predict the drift radius very well.Even though the numerical simulation results do not coincide well with the results of experiment in yaw direction,the program can give a rough estimation of the performance of the newly designed DPS and its subsystem.The efficiency of the numerical simulation is very high.Therefore,the program can be used as a main research tool to validate the newly designed dynamic positioning system.

5 Conclusions

In this study,a new software program DPTDSP which is able to conduct an‘experiment’to evaluate a new designed dynamic positioning system and subsystem in the MatlabSimulink environment has been proposed.In addition,the effectiveness of the developed Dynamic Positioning Time Domain Simulation Program,DPTDSP as a marine tool was investigated by a simplified model test on a dynamic positioned semi-submersible.The results showed that the program could predict the position and heading of the vessel,especially the drift radius well.It can be concluded that the program can be used as a main research tool to validate the new designed dynamic positioning system or its subsystem.

[1]Sørensen A J.A survey of dynamic positioning control systems[J].Annual Reviews in Control,2011,35:123-136.

[2]Mahfouz A B,El-Tahan H W.On the use of the capability polar plots program for dynamic positioning systems for marine vessels[J].Ocean Engineering,2006,33:1070-1089.

[3]Sørensen A J,Strand J P.Positioning of small-waterplane-area marine constructions with roll and pitch damping[J].Control Engineering Practice,2000,8:205-213.

[4]Fossen T I.Guidance and control of ocean vehicles[M].New York:John Wiley&Sons Inc,1994.

[5]Faltinsen O M.Sea loads on ships and offshore structures[M].Cambridge(UK):Cambridge University Press,1990.

[6]Fossen T I.Handbook of marine craft hydrodynamics and motion control[M].New York:John Wiley&Sons Inc,2011.

[7]Wichers J E W.A simulation model for a single point moored tanker[D].Dissertation of Technical University Delft,1988.

[8]Sørensen A J,Ronxss M.Mathematical modeling of dynamically positioned and thruster-assisted anchored marine vessels [C].In:The Ocean Engineering Handbook,Ferial El-Hawary Ed,2001.

[9]Isherwood R M.Wind resistance of merchant ships[J].R.I.N.A.Supplementary Papers,1973,115:327-338.

[10]Gosman A D.Developments in CFD for industrial and environmental applications in wind engineering[J].Journal of Wind Engineering and Industrial Aerodynamics,1999,81:21-39.

[11]Zhang S,Wang L,Yang S Z,Yang H.Numerical evaluation of wind loads on semi-submersible platform by CFD[C].In: ASME 2010 29th International Conference on Ocean,Offshore and Arctic Engineering,2010.

[12]Newman J N.Marine hydrodynamics[M].Cambridge(MA):MIT press,1977.

[13]Fossen T I,Strand J P.Passive nonlinear observer design for ships using Lyapunov methods:Full-scale experiments with a supply vessel[J].Automatica,1999,35:3-16.

[14]Johansen T A,Fossen T I,Berge S P.Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming[J].Control Systems Technology,IEEE Transactions,2004,12:211-216.

动力定位时时域模拟程序试验验证

徐胜文，王 磊，汪学锋，李 博

（上海交通大学 海洋工程国家重点实验室，上海 200240；高新船舶与深海开发装备协同创新中心（船海协创中心），上海 200240；上海交通大学 船舶海洋与建筑工程学院，上海 200240）

在启用新的动力定位系统时，数值和试验验证方法，包括静态动力定位能力分析、动态的时域模拟和模型试验应该用来设计，分析和预测新系统的性能。为了精确并经济地验证动力定位系统的性能，在MatlabSimulink环境中，开发了一个能够进行一个"试验"来评估一个新设计的动力定位系统和其子系统的程序。另外，这个新开发的动力定位时域模拟程序的可靠性通过对一个半潜平台的模型试验进行了评估。结果表明，这个程序可以作为一个船舶研究工具用来检验新设计的动力定位系统或其新模块。

动力定位系统；动力定位时域模拟程序；船舶研究工具

U661.3

A

徐胜文（1986-），男，博士，上海交通大学专职科研人员；

U661.3

A

10.3969/j.issn.1007-7294.2016.06.005

1007-7294（2016）06-0686-13

王 磊（1971-），男，上海交通大学副教授；

汪学锋（1966-），男，上海交通大学教授；

李 博（1987-），男，上海交通大学硕士。

Received date：2016-03-24

Foundation item:Supported by the National Key Basic Research Development Plan(973 Plan)Project of China (Grant No.2013CB036103)and Ministry of Industry and Information Technology(Floating structure position mooring technology research)

Biography:XÜ Sheng-wen(1986-),male,Ph.D.,researcher fellow of Shanghai Jiao Tong University;WANG Lei(1971-), male,associate professor;WANG Xue-feng(1966-),male,professor,E-mail:wangxuef@sjtu.edu.cn.