不同重构算法对压缩感知重构效果的影响

李瑞明，张烨，杨慧炯，原菊梅

（太原工业学院，山西 太原 030008）

1 引言

在医学成像、模式识别以及图像处理等领域，需要采集大量信息并且对其进行处理。传统的采样方法均基于Nyquist 采样定理，该采样方法所需采样数据量大（采样频率大于数据传输最高频率的二倍）、采样时间较长，并且存在压缩复杂度高、恢复算法不易实现的问题。

针对传统采样理论以及信号处理方法的不足，压缩感知理论逐渐得到广泛应用[1-3]，本文首先对压缩感知理论进行了阐述，然后以电能质量暂态信号中的电压突降为例，采用不同恢复算法对信号进行重构，并对不同算法的重构效果以及性能指标进行比较。

2 压缩感知理论

压缩感知理论的主要思路为：如果长度为N的一维源信号在某域内具有K——稀疏性（K＜N），则可对该信号进行压缩观测，进而采用恢复算法对稀疏观测后的矩阵进行重构。图1 为压缩感知理论的结构图：

图1 压缩感知理论基本结构

3 国内外研究现状

压缩感知理论将具有一定稀疏度的原始信号进行压缩观测，然后采用重构算法进行重构，这样既可以减弱对硬件的依赖程度，也可节约存储空间，降低数据的传输压力，因此受到了国内外专家的广泛关注[4]。

压缩感知理论包括三大核心问题：信号的稀疏性、压缩观测和重构算法。其中，源信号具有一定的稀疏度是进行压缩采样的前提，因此需要对源信号进行稀疏表示，然后进行压缩观测，要求其观测矩阵与稀疏基不相关，进而采用恢复算法对压缩观测矩阵进行重构。

3.1 信号的稀疏表示

由压缩感知理论可知，源信号的稀疏度决定了压缩采样个数和信号的重构效果，且是压缩理论应用的前提。信号的稀疏表示主要有稀疏字典与稀疏分解算法两种。其中，稀疏字典中的傅里叶变换在压缩感知算法的稀疏表示中应用最多，本文采用的稀疏基为傅里叶变换基。

3.2 观测矩阵

观测矩阵是实现压缩感知算法的关键。观测矩阵需要满足硬件容易实现、采样复杂度低、效果良好，并且要求观测矩阵与稀疏基具有不相关性。随机观测矩阵、确定性观测矩阵和自适应观测矩阵应用比较广泛[5]。

其中，随机观测矩阵采样复杂度比较高、硬件难实现，而确定性观测矩阵需要基于受限等距特性（Restricted Isometry Property，RIP）进行构造。文献[5]提出具有自适应性的观测矩阵，该矩阵与稀疏基矩阵具有很低的相关性，并且具有最优性，应用广泛。因此，本文利用自适应观测矩阵作为观测矩阵。

3.3 重构算法

对压缩观测后的信号重构即为求解最优问题。常用的重构算法有贪婪追踪算法、组合算法和凸松弛算法[6-7]。贪婪追踪算法包括匹配追踪（Matching Pursuit，MP）算法、正交匹配追踪（Orthogonal Matching Pursuit，OMP）算法、分段OMP 算法和正则化OMP 算法。该类算法的重构精度与算法复杂度相关。组合算法包括傅里叶采样、链追踪和HHS 追踪等。而凸松弛算法通过将非凸问题转化为凸问题进而逼近目标信号，主要包括BP 算法、内点法、梯度投影方法和迭代法，该类算法所需观测点数很少，不需要信号的稀疏度，且重构效果比较好。本文采用谱投影梯度算法作为恢复算法对信号进行重构。

4 不同重构算法重构效果的比较

一个可靠的供电系统包括三部分：电压波形为正弦波、幅值、频率恒定。但是不同种类的负荷会对电网造成干扰，影响供电质量，因此需要对电能质量扰动信号进行分析。由于传统采样方式存在的固有缺点，压缩感知理论逐渐被应用到电能质量扰动信号中来。但是压缩感知理论在电能质量扰动信号中为初步应用，只是涉及到信号压缩采样和原始信号的重构[8]。进行压缩采样时，采用傅里叶变换基、二维小波基作为稀疏矩阵，观测矩阵自适应观测矩阵，信号的重构算法则选用CoSaMP 算法、基于TV 最小化共轭梯度法、MP 算法、OMP 算法以及凸优化算法等作为重构算法对电能质量扰动信号进行重构。本文以电能质量电压突降扰动为例，分别采用OMP 算法、CoSaMP 算法、ROMP 算法以及SPG 重构算法对原始信号进行重构，重构效果如图2、3、4、5 所示。

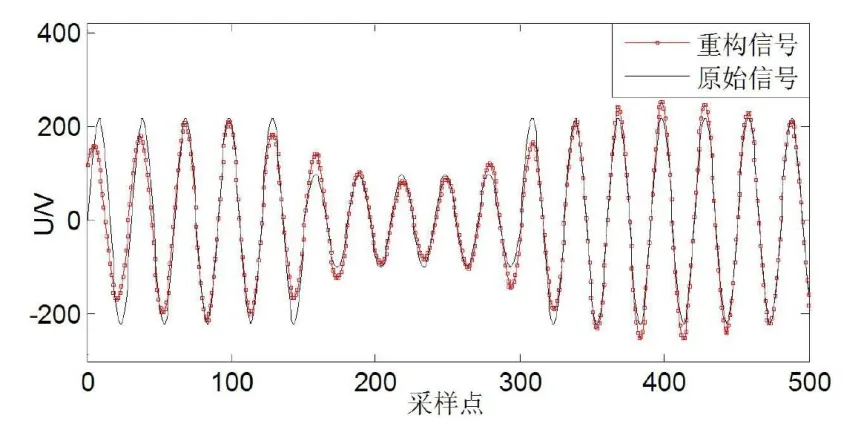
图2 基于OMP 算法的电压突降信号重构

图3 基于CoSaMP 算法的电压突降信号重构

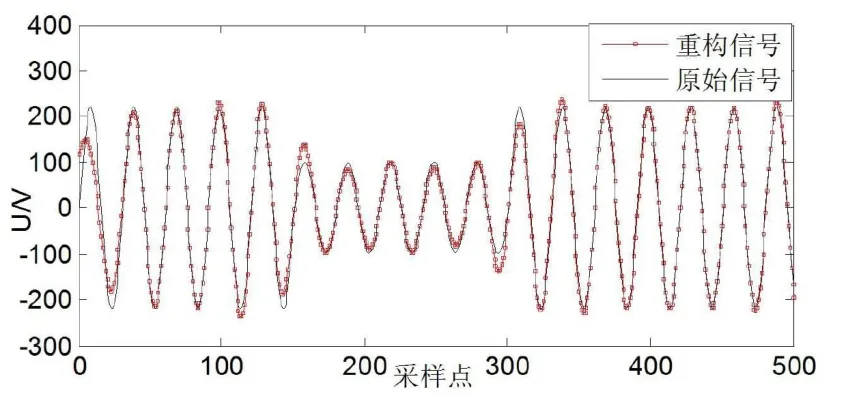
图4 基于ROMP 算法的电压突降信号重构

图5 基于SPG 算法的电压突降信号重构

由图2、3、4 可知，以OMP 算法、CoSaMP 算法、ROMP 算法为代表的贪婪算法在重构精度上相对较低，重构信号与源信号存在较大误差，而SPG算法由于运用谱投影梯度方法计算更新方向与步长，引进非单调性搜索策略使算法具有全局收敛性，从而达到了非常好的重构精度，并且该算法的运行效率非常好。由图5 可以看出，采用SPG 算法，重构信号与原始信号几乎完全重合，因此其重构精度远远高于OMP 算法、CoSaMP 算法、ROMP算法为代表的贪婪算法。

表1、2分别表示不同贪婪算法的压缩性能指标比较以及贪婪算法与凸优化算法的压缩性能指标比较。

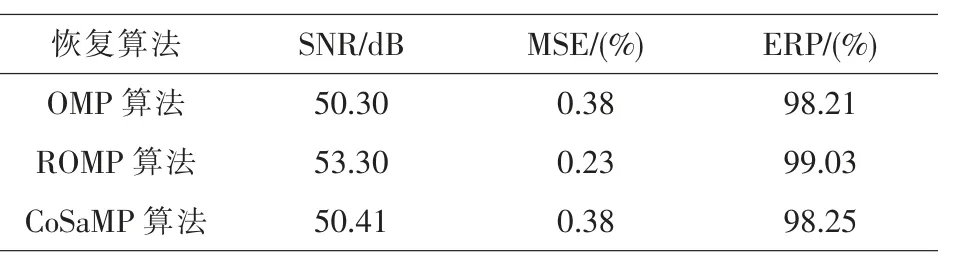
表1 贪婪算法的压缩性能比较

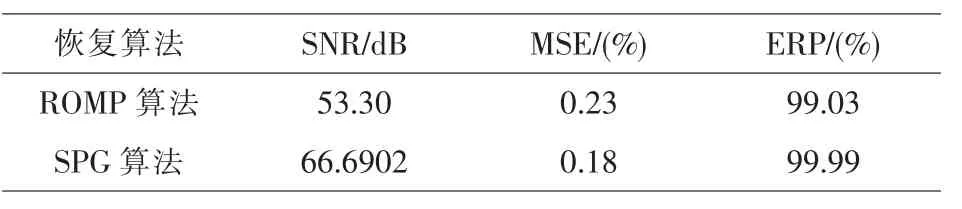
表2 贪婪算法与凸优化算法压缩性能比较

表1、2 分别为贪婪算法的压缩性能指标和贪婪算法与凸优化算法的压缩性能指标比较。可以看到，在贪婪算法中，CoSaMP 的SNR、MSE、ERP均高于其他算法。而以SPG 为代表的凸优化算法的压缩性能指标则高于贪婪算法，但是SPG 恢复算法由于算法复杂度比较高，因此运行时间相对要长一点。

5 总结

本文首先对压缩感知理论进行了阐述，重点分析了其恢复算法，最后以电压突降信号为例，采用不同恢复算法对其进行重构，并对不同算法的重构效果以及压缩性能指标进行了比较与分析。由结果可以看出，以SPG 算法为代表的凸松弛算法的重构效果以及压缩性能指标高于OMP 算法、CoSaMP算法、ROMP 算法。课题下一步的研究方向为对发生扰动的信号时间进行判断，即进行扰动的定位。