构造法在高中数学圆锥曲线解题中的巧妙运用
☉江苏省常熟市尚湖高级中学程建刚
构造法在高中数学圆锥曲线解题中的巧妙运用
☉江苏省常熟市尚湖高级中学程建刚
随着经济的发展和科学技术的进步,社会各领域对人才的竞争越发激烈.为了培养新时代优秀人才,教育教学的研究势在必行.由于数学知识在现实生活中的应用逐渐加大,而圆锥曲线部分在高中数学的知识地位不可替代,并且构造法是教师进行数学教学的一种重要的思想方法,因此,运用构造法来解决圆锥曲线问题具有重要的意义.下面,本文将探析构造法在高中数学圆锥曲线解题中的应用.
一、构造图形法
在解决一些数学问题时,由于不能直接从已知的数据中得出答案,而可以根据题中给出的已知条件或结论构造出相关的图形来获得结果,这样的方法就是构造图形法.[1]教师运用这种方法教学,可以充分利用图形的直观性特点,将形象思维与逻辑思维紧密结合在一起,让学生尽快地进入到题目情景中去,并最终解决问题.
例1设F1、F2分别是椭圆的两个焦点,若在此椭圆上存在一点P使∠F1PF2=90°,求离心率e的范围.
解法1:点P在以F1F2为直径的圆上,又点P在椭圆上,固有c≥b.
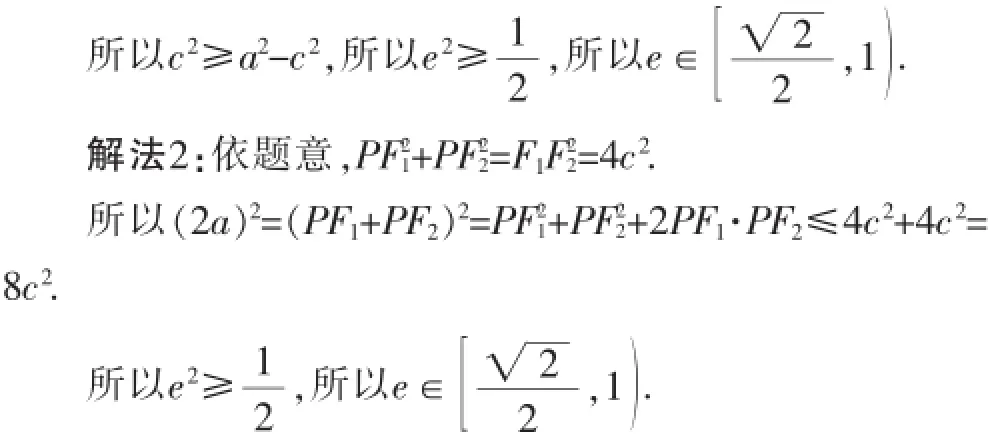
点评:通过两种方法对比,我们不难发现,解法1是从几何角度来研究问题的,就是最大限度地利用图形条件.运用这样的构造方法,往往能够省去很多不必要的运算.
例2一炮弹在A处的东偏北60°的某处爆炸,在A处测到爆炸信号的时间比B处早4秒,已知A在B的正东方,相距6千米,P为爆炸地点,该信号的传播速度为每秒1千米,求A、P两地的距离.
分析:利用构造图形的方法,先判断出P点的轨迹为双曲线右支上的一点,然后通过P在A的东偏北60°方向,求出P点的坐标,再根据两点间的距离公式便能求出A、P两地的距离.
解:如图1,以直线AB为x轴,线段AB的垂直平分线为y轴,建立直角坐标系,则A(3,0),B(-3,0).
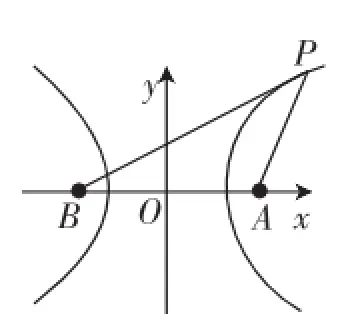
图1

点评:通过构造出题目中所需要的图形,可以很直观地面对问题,从而较快地找出解决办法,免去了许多的麻烦,提高了解题效率.
二、构造命题法
该方法主要用于在论证某些命题而感到没有直接依据或比较困难时,以此来解决问题.中心轨迹关于点M(-1,1)对称图形的轨迹方程.
引用命题:已知曲线方程f(x,y),则它关于点M(x0,y0)对称的曲线方程是f(2x0-x,2y0-y)=0.(证明略)
解析:设椭圆中心为(x,y),根据题意,有x=2t,y=-t2.
消去参数得椭圆中心轨迹方程为f(x,y)=x2+4y=0.
由上可知,它关于M(-1,1)对称图形的轨迹方程为f(-2-x,2-y)=0,即(-2-x)2+4(2-y)=0,化为(x+2)2=4(2-y),即为所求的轨迹方程.
点评:由于题中没有直接给出曲线方程关于一个点对称的方程式,采用这种构造法,可以很快地打开解题思路,最终解决问题.
例3设椭圆方点P1、P2,求线段P1P2的中点P的轨迹方程.
引用命题:过定点P(x0,y0)的动直线l与二次曲线C:F(x,y)=0相交弦的中点轨迹方程是F(x,y)=F′(x0,y0).(证明略)
点评:该题如上题一样,都可使用构造命题的方法来解决.
三、构造方程法
构造方程法,就是根据问题的结构特征及其数量关系,挖掘潜在的已知和未知因素,从而构造出方程,使问题能够巧妙地解答出来.
例5已知△ABC的顶点A、B在椭圆x2+3y2=4上,顶点C在直线l:y=x+2上,且AB∥l.求:
(1)当AB边通过坐标原点O时,求AB的长及△ABC的面积;
(2)当∠ABC=90°,且斜边AC的长最大时,求AB所在直线的方程.
分析:本题要准确把握好直线l的位置,将题中的几何信息转化为代数方程法,将几何问题变成解方程问题,能够使问题简单化,有利于快速地得出答案.[2]
解:(1)因为AB∥l,且AB通过原点(0,0),所以AB所在直线的方程为y=x.
设A、B两点的坐标分别为(x1,y1)、(x2,y2).
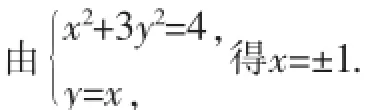

所以|AC|2=|AB|2+|BC|2=-m2-2m+10=-(m+1)2+11.
所以,当m=-1时,AC边最长(这时Δ=52>0),此时AB所在直线方程为y=x-1.
例6已知抛物线C1:y=x2+2x和抛物线C2:y=-x2+a,当a取什么值时,C1和C2有且仅有一条公切线,写出公切线的方程.

四、构造函数法
从初中我们就开始接触函数,对于函数的性质和特点等都有了比较深刻的了解.选择用最熟悉的方式来解决圆锥曲线问题,必然是一种不错的选择.
例7已知圆C1:x2+(y-2)2=1,直线l:y=-1,有一动圆C与C1外切,且与直线l相切.
(1)求动圆圆心C的轨迹M的方程;
(2)直线l与轨迹M在第一象限相切,其切点为P,直线l的斜率为k,过点P作直线l的垂线恰好经过点A(0,6),并与轨迹M相交于点Q(P与Q不重合),设S为△POQ(O为坐标原点)的面积,求S的值.

因为点P在第一象限,所以x0=4,点P的坐标为(4,2),直线PQ的方程为x+y-6=0.
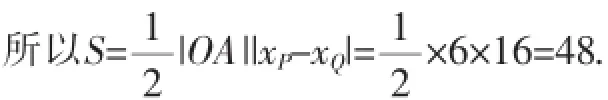
点评:该题第(1)问中,主要通过判断圆C的位置,来进一步确定y+1>0;第(2)问,主要运用了构造导数函数的方法,利用切点处的导数为直线的斜率得出直线方程,后通过已知点求出切点坐标.
五、构造不等式关系
在圆锥曲线解析中,构造不等式关系主要是针对求值范围问题.[3]在解题过程中要充分理解已知条件,挖掘其隐含条件来构造不等式.
分析:在本题中,绝大多数同学由于对题目的整体把握不够,以至于做到一半无法继续进行.其实,该取值范围可通过构造关于所求量的不等式关系来获取.构造不等式首先要考虑判别式——由判别式值的非负性可以很快确定k的取值范围.

点评:对于范围问题,还可以用其他途径来建立不等关系,比如函数的性质法、均值不等式法等.本题采取构建判别式不等关系法,使得解题思路清晰明了,避免了解题方式冗杂,提高了解题效率.
六、总结
在解决圆锥曲线问题时,我们首先要大致辨识题目所要考查的知识点,以便与已掌握的知识建立联系,从而根据已有的知识经验进行求解,这在一定程度上减少了盲目解题的可能性.接下来就是选取合适的解决方法:问题的解决有多种方式.但是,在这里,运用构造法的解题方式,就是要改变解题过程中的呆板模式,善于找到数与形、数与量、数与方程等之间的内在联系,开阔思维,用多元化的方法来处理解决圆锥曲线问题.
1.庄丰.圆锥曲线问题中减少运算量的利器——构造法[J].中小学数学(高中版),2015(10).
2.高小山,蒋鲲.用圆锥曲线求解几何约束问题[J].中国图象图形学报,2001(6).
3.李学武,丁玉民.构造法解圆锥曲线中的范围问题[J].数理化学习(高中版),2007(Z1).F

