全面践行数学核心素养——《三角函数的应用》教学实录

☉江苏省锡山高级中学陈敏☉江苏省锡山高级中学方莉

全面践行数学核心素养
——《三角函数的应用》教学实录

☉江苏省锡山高级中学陈敏☉江苏省锡山高级中学方莉

数学核心素养是具有数学基本特征的、适应个人终身发展和社会发展需要的人的关键能力与必备品质.也就是个体面对复杂的、不确定的情境时，综合运用数学知识、观念、方法解决实际问题所表现出来的关键能力与必备品质.东北师范大学史宁中教授与首都师范大学王尚志教授在修订《普通高中数学课程标准（实验）》时，认为数学核心素养主要包括数学抽象、运算能力、逻辑推理、数学建模、直观想象、数据分析等几个方面.用一句话概括，就是“用数学眼光观察世界，用数学思维分析世界，用数学语言表达世界”.

数学建模是对现实问题进行抽象，用数学语言表达问题、用数学知识与方法构建模型解决问题的过程.主要包括：在实际情境中从数学的视角发现问题、提出问题、分析问题、建构模型、求解结论、验证结果并改进模型，最终解决实际问题.数学模型构建了数学与外部世界的桥梁，是数学应用的重要形式.数学建模是应用数学解决实际问题的基本手段和推动数学发展的重要动力.

数学建模活动是运用模型思想解决实际问题的综合实践活动，是高中数学课程的重要内容，在数学建模活动过程中，逐步提升数学建模、数学抽象、数据分析、数学运算、逻辑推理和直观想象素养，可以说数学建模活动全面指向数学核心素养的发展.

现实生活中有许多周期现象，如弹簧振子、摩天轮、大海潮汐、日出日落、月圆月缺、四季交替、人体节律变化等都可以用三角函数进行模拟，三角函数在解决实际问题中有着广泛的应用.通过这部分内容的教学，能很好地培养学生“数学地观察、数学地思考、数学地表达”的习惯，全面践行数学核心素养.

用三角函数模型解决实际问题的基本步骤如下：

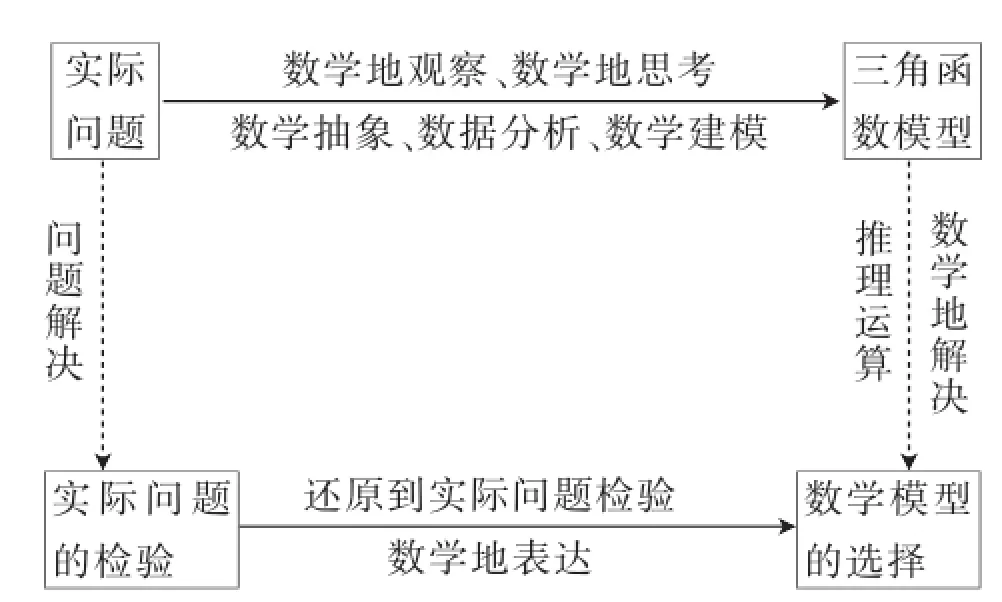
以上解决实际问题的基本步骤的“内环”就是数学核心素养的主要方面，“外环”就是数学核心素养的一句话概括.

下面以高中数学苏教版《三角函数的应用》课堂实录为例具体说明，以飨读者.

教学实录：

我们知道物体做简谐运动时，位移s和时间t的关系式为s=Asin（ωt+φ）（A＞0，ω＞0），如弹簧振子，现实生活中还有许多周期现象，如摩天轮、大海潮汐等也可以用三角函数进行模拟吗？这节课我们就来探讨三角函数的应用.

设计意图：指出三角函数能够模拟许多周期现象，它在解决实际问题中有着广泛的应用，引出课题.

一、课题引入

引例：如图1，点O为做简谐运动的物体的平衡位置，取向右的方向为物体位移的正方向，若已知振幅为3cm，周期为3s，且物体向右运动到距平衡位置最远处时开始计时.

（1）求物体对平衡位置的位移x（cm）和时间t（s）之间的函数关系；

（2）求该物体在t=5s时的位置.

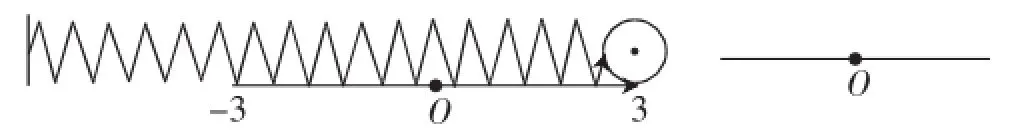
图1

呈现方式：用Flash动画演示弹簧振子的周期运动，并形成三角函数曲线运动轨迹.

设计意图：引例比较简单，通过引例的解决，学生大致形成用三角函数模型在解决实际问题的基本步骤.

师生互动：教学中设置“问题串”引导学生步步思考，层层深入.

师：根据物理知识和前面所学的知识，应选择怎样的函数模拟物体的运动？

生1：用函数x=Asin（ωt+φ）（A＞0，ω＞0，0≤φ＜2π）来表示简谐运动物体对平衡位置的位移x（cm）和时间t（s）之间的函数关系.

师：由已知条件怎样求A、ω和初相φ？物体向右运动到距平衡位置最远处时开始计时的数学含义是什么？

师：该物体在t=5s时的位置在哪里？

二、数学建构

学生回顾引例的解决过程，试着总结出用三角函数模型解决实际问题的基本步骤.

三、数学运用

游乐场里的摩天轮，用于发电的大风车，随水而转的水轮这些都是生活中常见的，能否用三角函数进行模拟？若可以，按照三角函数模型解决实际问题的基本步骤，可以解决一些相关问题.

教材原题:

如图2，一个半径为3m的水轮，水轮圆心O在水面上方且距离水面2m，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计算时间.

图2

（1）将点P距离水面的高度Z（m）表示为时间t（s）的函数；

（2）点P第一次到达最高点大约要多长时间？%

这是苏教版教材中的原题，考虑到该水轮的圆心不在水面上，学生理解上有些困难，再加上φ不是特殊角，计算起来数据也比较烦琐，考虑到无锡学生熟悉的生活环境，使问题解决有坡度，笔者搭了一个“脚手架”，铺设了一个台阶，这样学生就可以拾级而上，数学思维层层递进.

呈现方式：几何画板动态演示水轮的转动以及P点离水面的高度随时间的变化轨迹.

设计意图：教师一个重要的任务就是把数学的学术形态转化为学生易于接受的教育形态，以学生为中心，遵循学生的认知规律，“蹲下来”从学生的角度出发，适当搭设思维的“脚手架”——接题.

教材原题的入口衔接：

例1如图3，美丽的蠡湖湖畔有一个半径为3m的水轮，水轮圆心O恰在水面上，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计算时间.试将点P距离水面的高度z（m）表示为时间t（s）的函数；

图3

思考一：几何画板动态演示水轮的转动以及P点离水面的高度随时间的变化轨迹表明，点P距离水面的高度Z关于时间t的函数关系式为z=Asin（ωt+φ）（A＞0，ω＞0），然后根据A，ω，φ各自的物理意义求之.

思考二：利用点P距离水面的高度与P点的纵坐标的关系，根据任意角三角函数的定义解决.

本题中，建立坐标系，用P点转过的角来表示P点的纵坐标是解题的重点和难点，为此笔者设计了如下教学过程：

师：水轮每分钟逆时针转动4圈，那么t秒钟转过的角是多少？

师：根据任意角三角函数的定义，P点距水面的高度与P点转过的角度有何联系？

生2：P点距地面的高度与P点转过的角度的正弦值有关.

师：笔者们可以尝试利用三角函数定义来解决，先建立平面直角坐标系，再利用P点的纵坐标来表示P距离水面的高度，如何用P点转过的角来表示P点的纵坐标呢？

生3：建立如图所示的坐标系，P点经过t秒后对应的以Ox为始边，OP为终边的

有了上述“脚手架”，教材中原来的例题的解决便水到渠成.

教材原题的优化改进：

考虑到教材中原来的例题的数据是一个近似值，可以在符合实际意义的前提下加以优化改进（如图4），把水轮圆心O在水面上方且距离水面2m改为P点纵坐标特殊角，没有降低数学思维的考查要求，而计算起来就方便多了.

图4

变式：一个半径为3m的水轮，水轮圆心O在水面上方且距离水面1.5m，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计算时间.

（1）将点P距离水面的高度z（m）表示为时间t（s）的函数；

（2）点P第一次到达最高点需要多长时间？

解：（1）方法一：设函数关系式为z=Asin（ωt+φ）（A＞0，ω＞0），然后根据A，ω，φ各自的物理意义求之.

方法二：利用点P距离水面的高度与P点的纵坐标的关系，根据任意角三角函数的定义解决.

设计意图：教材例题解决了不能就此作罢，为进一步挖掘它的教育教学功能，可以在教材例题改编的基础上更进一步，设计一个意境优美的问题考查学生三角不等式的解法，也为接下来海水潮汐问题埋下伏笔.同时也大大提高了学生的学习兴趣.

教师追问：假设这鸟儿只顾欣赏美景，不小心被卡在点P处不能动弹，而且这只鸟儿在水中一次憋气最长4秒钟，从爱护鸟类的角度考虑，结合本题的三角函数模型，你能设计一个问题吗？

学生异常兴奋，积极思考，踊跃发言.

学生设计问题：水轮每分钟至少转几圈，这只鸟儿才不会被憋死？

事实上，设水轮每分钟至少转n圈，则每秒钟转过=5（s），故点P第一次到达最高点需要5s.

教材原题的拓展延伸：

拓展：美丽的蠡湖湖畔有一个半径为3m的水轮，水轮圆心O在水面上方且距离水面1.5m，已知水轮每分钟逆时针转动4圈，如果当水轮上点P从水中浮现时（图中点P0）开始计算时间.假设一只鸟儿在点P处，而且它离水面至少3m才能鸟瞰蠡湖全景，试问这只鸟儿饱览蠡湖全景的时间有多长？

设计意图：增强学生提出问题的意识和能力，同时也呼唤学生善待生命的仁爱之心以及人与自然和谐相处的环保意识.

例1小结：圆周运动可以用三角函数模拟，要注意结合任意角三角函数的关系以及和物理中简谐运动的相关知识求出三角函数关系式，通过建立三角方程或三角不等式解决相关实际问题.

四、拓展探究

例2（根据教材《探究案例：港口水深的变化与三角函数》改编）

海水受日月的引力，在一定的时候发生涨落的现象叫潮汐，一般地，早潮叫潮，晚潮叫汐.下表是某港口某一天从0:00时至24:00时记录的时间t（h）与水深y（m）的关系如下表：

时刻0 : 0 0 3 : 0 0 6 : 0 0 9 : 0 0 1 2 : 0 0 1 5 : 0 0 1 8 : 0 0 2 1 : 0 0 2 4 : 0 0水深1 0 . 0 1 3 . 0 9 . 9 7 . 0 1 0 . 0 1 3 . 0 1 0 . 1 7 . 0 1 0 . 0

（1）选用一个函数来近似描述这个港口的水深与时间的函数关系.

（2）一条货船的吃水深度（船底与水面的距离）为7m，安全条例规定至少要有4.5米的安全间隙（船底与海底的距离），船舶在港内停留时可以不考虑安全间隙，那么该船在什么时候可以进港？若该船要当天安全离港，一次进港后，它在港内停留最多不能超过多长时间？

呈现方式：几何画板动态演示海港的潮汐现象；利用Excel画出散点图.

分析：对表中的数据进行分析，作出散点图.从散点图的形状可以判断，这个港口的水深与时间的关系可以用形如y=Asin（ωx+φ）+h的函数来刻画.其中x是时间，y是水深，根据数据可以具体确定A，ω，φ，h的值.

解析：（1）以时间为横坐标，水深为纵坐标，画出散点图（如图5）.

根据图象，可以考虑用函数y=Asin（ωx+φ）+h刻画水深于时间之间的对应关系.从数据和图像可以得出：A=口的水深与时间的函数关系可［0，24］近似描述.由上述关系易得港口在整点时水深的近似值.

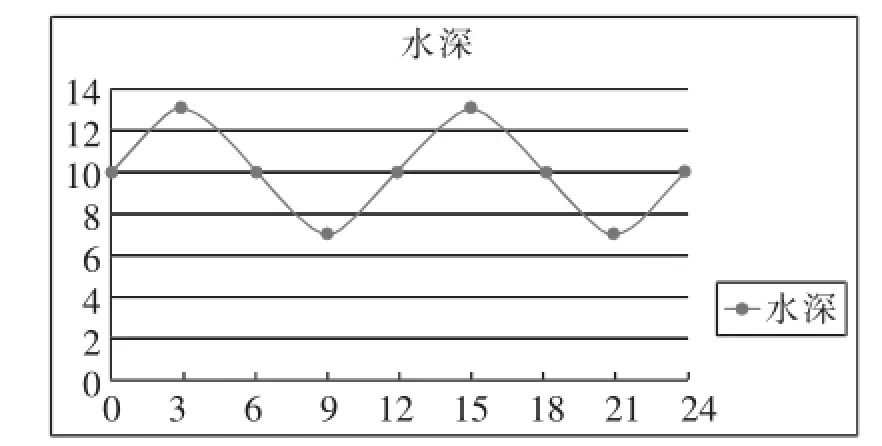
图5

（2）货船需要的安全水深为7+4.5=11.5（m），

所以当y≥11.5时就可以进港.

设计意图：苏教版教材中《探究案例：港口水深的变化与三角函数》，叙述烦琐，数据复杂，学生不易理解，在不减少考查内容、不降低考查要求的前提下，笔者“得其意，忘其形”，进行了改编.

例2小结：用三角函数拟合实际问题一般步骤为：（1）画散点图；（2）确定拟合函数；（3）构建三角函数或三角不等式；（4）回到实际问题检验说明.

五、课堂小结

三角函数在解决具有周期现象的实际问题中有着广泛的应用.本节课同学们通过建立三角函数模型，解决了一些实际问题，体现了数学建模的思想，提高了数据分析处理的能力，基本掌握了用三角函数模型解决实际问题的主要步骤，有了初步的实际问题数学化的意识与能力.希望同学们平时能够数学地观察、数学地思考、数学地解决、数学地表达！

六、作业布置

除本节课设计的弹簧振子、水轮圆周运动、大海潮起潮落外，生活中还存在着大量的周期现象，如日出日落、月圆月缺、四季交替、脉搏跳动、人体节律变化、波的传播、交流电等等，请你就某一个周期现象留心观察，采集、分析、处理数据，深入思考，建立三角函数模型数学地解决，撰写一份研究报告.G