高速列车故障轴箱轴承的温度分布研究

汤武初， 王敏杰， 陈光东， 孙玉超， 许 立

(1. 大连理工大学 机械工程学院， 辽宁 大连 116021；2. 大连交通大学 机械工程学院， 辽宁 大连 116028)

随着高速铁路的迅猛发展，高速列车的安全性受到极大重视。轴箱轴承作为高速列车走行部的核心部件，对其性能研究有很重要的意义。轴承温度的升高直接影响轴承寿命，只有了解轴承内部温度分布及影响因素，才能对轴承制定合理的润滑和冷却方案[1]。

国内外主要通过边界元法、有限分析法及有限容积法对高速列车制动盘及轴承温度场进行分析[2-3]。本文采用热网络法、有限元分析法并通过实验对高速铁路轴箱轴承在实际运转中最易出现的几种失效形式进行研究，并分析不同失效轴承的温度分布及影响轴承温度的主要因素。为高速列车在线温度监测系统提供一定的依据，并为我国高铁轴承国产化发展提供必要的技术支撑。

1 双列圆锥滚子轴承的热分析理论

1.1 轴箱轴承的主要发热来源

轴箱轴承的主要热源为[4-6]：滚动体与内外圈滚道之间的摩擦；保持架与外圈引导面之间的摩擦；滚子与保持架兜孔之间的摩擦；滚子端面与挡边之间的摩擦；润滑剂的黏性摩擦。由此可知热源是由于各部件之间的摩擦引起的，轴承工作时产生摩擦，摩擦生成热量，最终引起轴承温度的升高，这是轴承发热过程。轴承的摩擦损失均转换为热量，而这些热量可以由阻力矩即摩擦力矩或轴承各部件的运动关系进行衡量。

1.2 圆锥滚子轴承生热量计算

(1) 整体法轴承生热量计算

利用经验公式及实验结果总结得出的的轴承摩擦力矩和轴承转速相乘便可得出轴承的整体生热，简称整体法。滚动轴承的摩擦损失在轴承内部几乎全部转化为热量，圆锥滚子轴承摩擦力矩由外力引起的摩擦力矩和黏性摩擦力矩2部分组成。

Palmgren通过实验确定由外力引起的摩擦力矩，其经验式为[7]

( 1 )

式中：f1表示载荷系数；p1表示轴承外力；dm表示节圆直径；a、b值取决于轴承类型的指数，对于圆锥滚子轴承a=b=1。润滑条件下滚动轴承的黏性摩擦力计算非常复杂，实际应用中使用较多的是简化后的黏性摩擦力矩经验式，其表达式为

( 2 )

( 3 )

式中：f0表示考虑轴承结构和润滑方式的摩擦系数；v为油或脂基础油的工作黏度；n表示轴承转速。

通过上式可计算出轴承的总摩擦力矩为

M=M1+M0

( 4 )

则轴承不同转速时的功率损耗计算式为[8]

H=1.047×10-4×Mn

( 5 )

式中：H表示因摩擦而消耗的功率，W；M表示摩擦力矩，N·mm；n表示轴承转速，r/min。

(2) 局部法计算摩擦热流量

局部法计算摩擦热流量是根据轴承各部件的运动关系，分别计算轴承各接触区域内每对接触对的局部摩擦热流量，计算结果更接近于实际工况，滚动轴承各接触处的摩擦热流量为

q=μpvs

( 6 )

式中：q表示摩擦热流量，W/m2；μ表示摩擦系数；p表示滚动体与外圈或内圈的接触载荷，N/m2；vs表示滚动体与外圈或内圈的相对滑动速度，m/s。

1.3 基于热网络法轴承温度分析

采用热网络法分析轴承温度需假设：(1)轴承各部件轴向温度相同；(2)润滑油及环境温度分别作为不同热节点。选取垂直于圆锥滚子轴承轴线的截面进行分析，轴承的温度热节点划分见图1,其各个热节点温度含义见表1。

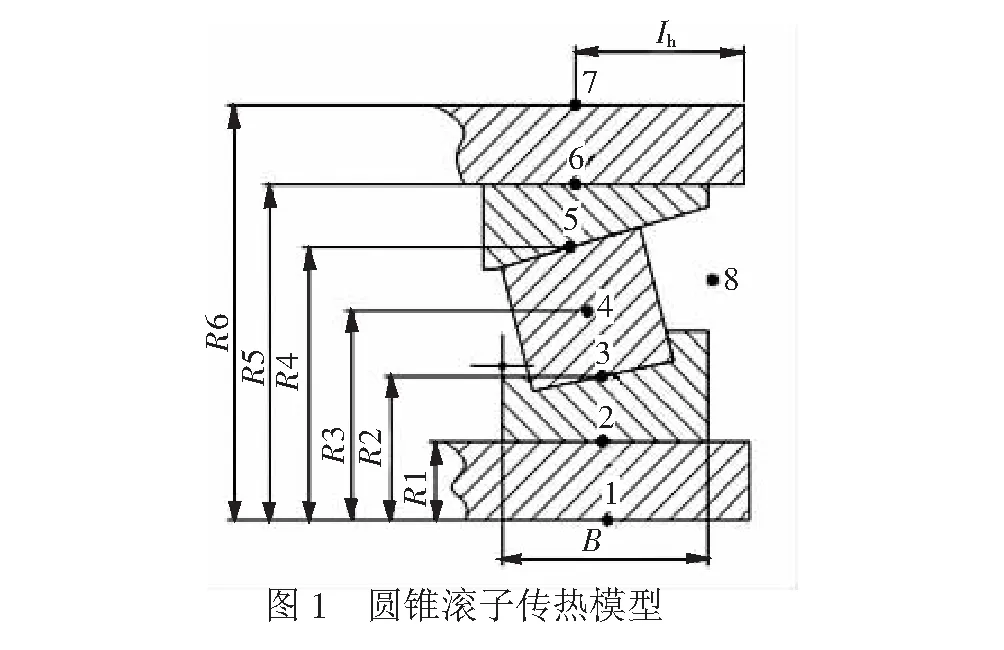
图1中，R1为轴承内径半径值;R2为滚动体与内圈滚道接触点到轴承中心距离；R3为滚动体自转中心到轴承中心的距离；R4为滚动体与外圈滚道接触处到轴承中心距离；R5为轴承外圈半径值；R6为轴箱体距轴承中心距离；B为轴承内圈宽度；Lh为轴箱体与空气接触端面距轴承外圈与滚道接触点间的距离；点1～8为温度热节点。

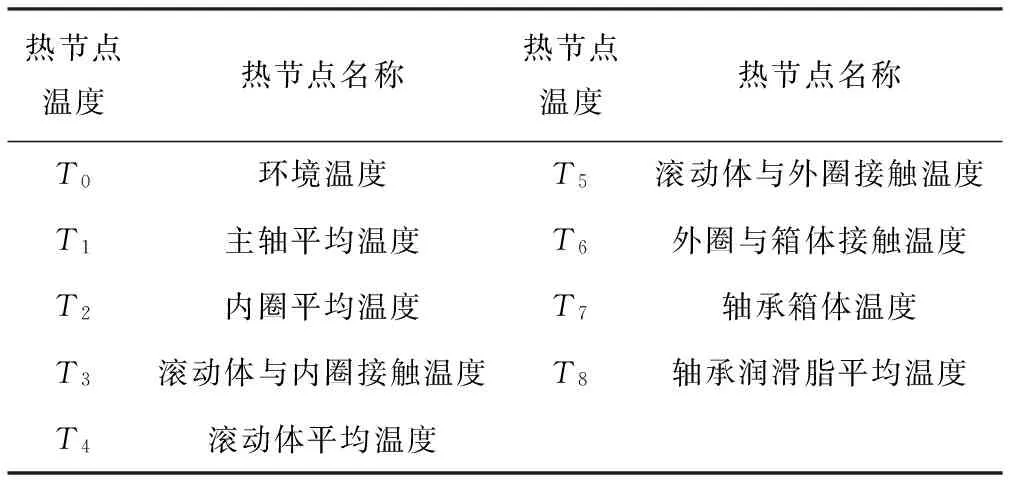
表1 圆锥滚子轴承热节点所代表位置温度

根据轴承在实际运转过程中的热量传递关系和各节点之间的对流换热等，可以列出圆锥滚子轴承的热流方程组

( 7 )

式中：R表示热阻，其下标中的字母c和v分别表示“传导”和“对流”，数字表示节点号；Qi为内圈滚道摩擦热；Qo为外圈滚道摩擦热。

联立式( 6 )、式( 7 )，便可计算出不同工况下轴承各个节点的温度分布情况,计算结果见表2。

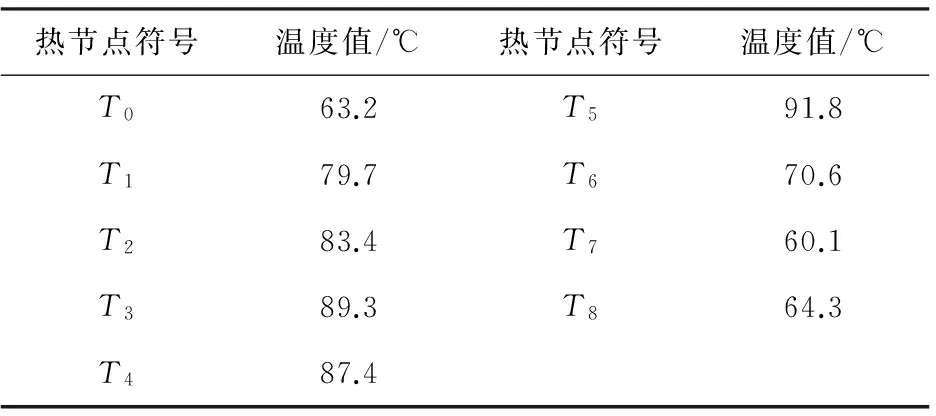
表2 热网络法计算轴承稳态温度分布结果

通过热网络法的计算结果可以看出，轴承在高速运行时的最高温度出现在轴承外圈与滚动体接触区域，最低温度出现在轴承箱体外表面。

2 基于ANSYS的双列圆锥滚子轴承温度场分析

2.1 建立有限元模型

选择我国CRH3型高速列车轴箱轴承TBU-BT2-8545-AD的SKF轴承，在ANSYS中建立三维模型，轴承详细参数见表3。考虑轴承的对称性，对1/2轴承进行实体建模[9]。在建模过程中，先建立分析模型中所需要的关键点，然后依次生成线和面，最终生成所需的三维实体； 再对模型进行网格划分。 为了保证网

格的质量使计算更准确，定义每条线细化成3 mm长度并进行网格划分，划出面网格后再通过扫略对整个轴承进行网格划分即得到了质量较高的六面体网格，并对滚子与内外圈接触区域进行局部网格细化以便提高计算的准确性和节约计算时间。通过PREP7前处理器对模型单元类型进行定义，轴承实体单元采用Brick 8 node 70单元，轴承各接触处均采用Targe170和Conta174单元定义，然后定义单元选项及实常数。将轴承实体单元的网格类型定义完成后需定义轴承各部分的材料热属性，定义轴承内外圈材料的导热系数为49 W/(m·℃)，滚动体导热系数为80 W/(m·℃)，比热容均为460 kJ/(kg·℃),密度为7.85×103kg/m3。

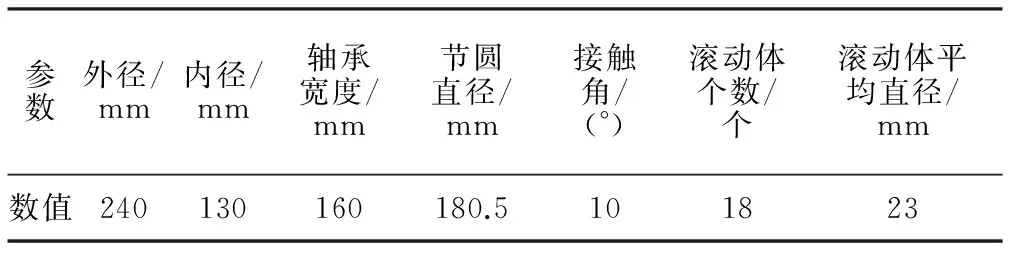
表3 圆锥滚子轴承相关尺寸技术参数

2.2 加载有限元模型

轴承热载荷是通过摩擦热流量进行加载的，通过查阅SKF、FAG等厂家资料，轴承正常工作下，滚动摩擦因数为0.001～0.002[9]。考虑到轴承在装配时，外圈与刚性很强的轴箱之间采用过盈配合装配，设置外圈转速为零。理论计算得出轴承外圈各个节点上所受到的载荷，再联合计算得出外圈相对于滚子的速度，便得到每个节点位置上的摩擦热流量；由于内圈随列车车轴一起转动，因此内圈受到交变载荷作用，即内圈受到周期性热载荷。通过计算载荷周期和载荷变化规律，得出内圈一个周期内产生的总热流量，最终把总热流量与一个周期所用时间的比值就能得到该区域的平均热量。

本文对滚子与内外圈的接触定义是：通过Hertz接触理论计算分析，得到接触区域面积，采用面-面接触方式定义。轴承在工作中内圈与车轴、外圈与轴箱之间通过热传导进行热量交换，采用热对流对轴承内圈及外圈外表面进行边界限制，最终完成轴承热分析有限元模型的加载。

2.3 求解有限元模型

共选取5个变量来表示轴承的不同种类的故障情况。为更有效直接地观测出每一个因素的影响及分析出各个因素的影响程度，最终采用正交试验法对这5种因素进行仿真求解。共需8组仿真求解即能满足分析要求，各组的仿真参数见表4。

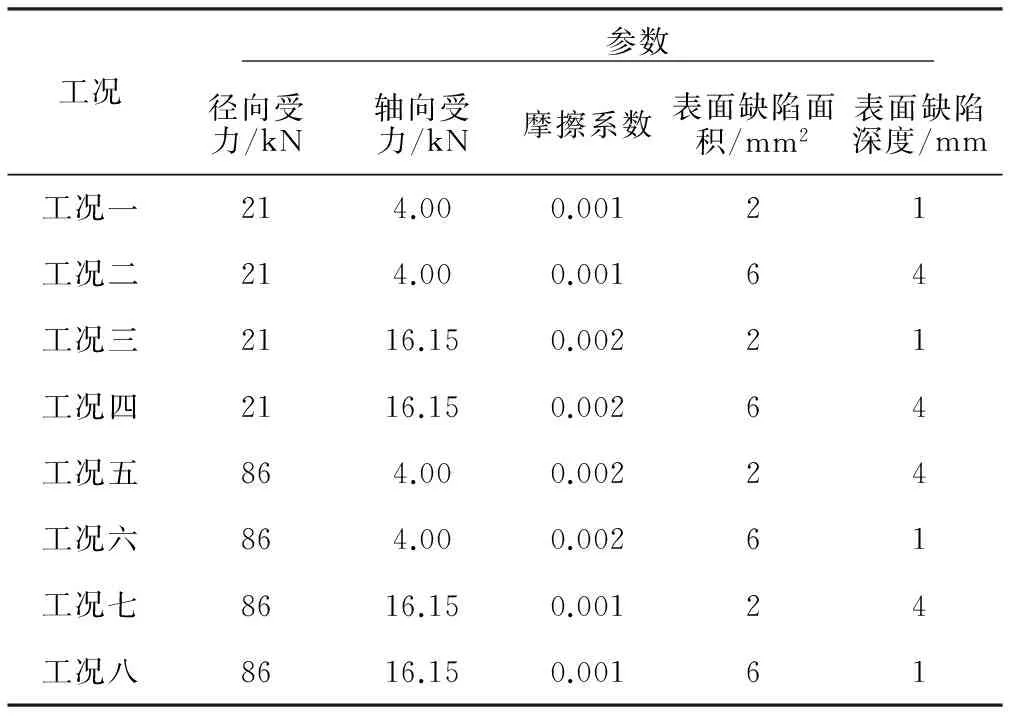
表4 不同工况下相关参数

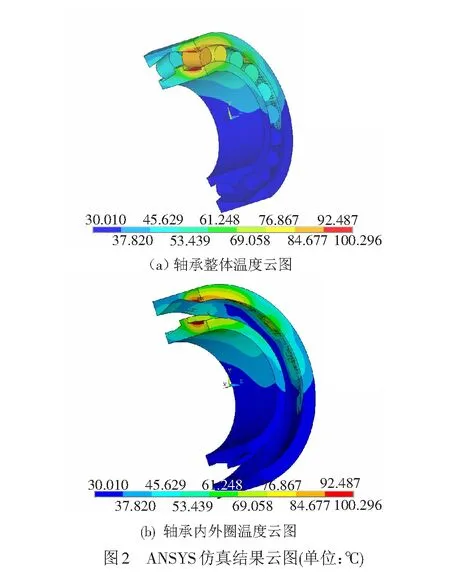
ANSYS仿真工况三的温度云图见图2。由云图2可以看出，轴承最高温度出现在外圈最上端的内滚道上，并且两列滚子在同一角度位置上的温度明显不同。该结果与高速铁路轴箱轴承的承载方式有密切关系，由于车厢的质量是经过一级悬挂系统和二级悬挂系统传递给转向架的轴箱，轴箱轴承再将力传递给车轴，车轴再通过轮对直接跟轮轨接触。因此可判断出轴承承载区是上半区，最大受力点在最上端的滚动体与外圈接触处。最上端周围的滚动体随位置角度的增加所受到的载荷逐渐减小，最上端的滚子在运动中受力和摩擦是最大的，摩擦越大产生的摩擦力矩也就越大，则产生的热量最多。其他滚子随位置角的逐渐增大生热量逐渐减小，所以轴承的热量分布上总体呈“上高下低”分布。沿轴向方向，两列滚子温差大是由于所受到的轴向力不同，承受大部分轴向力的一列，摩擦力矩也大，其温度也高于另一列，即出现图2温度分布。

3 轴承温度数据处理

通过上述温度模型，依次对这8种工况进行有限元仿真分析。为了保证仿真的稳定性和一致性，在轴承的外圈表面分别布置5个测温点，见图3，测点5为轴承最上端点，其余各测点角度相差12.5°。通过这5个测点的温度大小进行数据处理分析，各组的试验结果见表5。

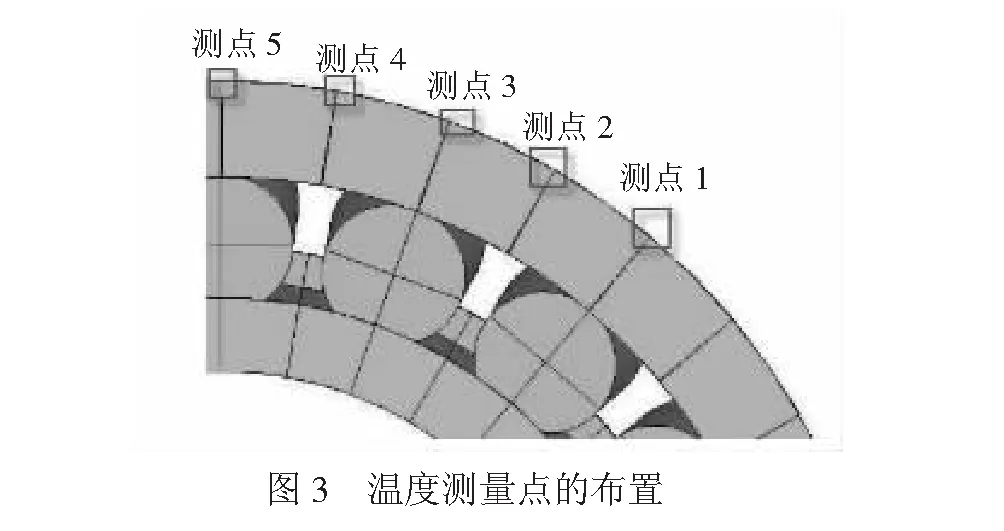
表5 各工况下各个测量点处的温度值

为了便于更直观地分析、计算，将上述各点温度值与正交试验表列在一起组成一个新表格。由于测点的温度值较大，将所测温度值减去50。选取测点5温度数据为例输入正交试验分析表(见表6)进行分析。

表6中的K1表示各个因素在第一水平时对应编号组的温度之和；K2表示各个因素在第二水平时对应编组的轴承温度之和；k1、k2分别表示2种水平温度的平均值。极差是最大值减去最小值得到的差，在统计中常用极差来刻画一组数据的离散程度及变量分布的变异范围和离散幅度。它能体现一组数据波动的范围。极差越大，离散程度越大，反之，离散程度越小。

按照上述方法进行计算，将每个因素的各个水平及每个测点的温度数据进行对比。各个测点所得结果如测点5类似，即极差最大的是轴承的摩擦系数，说明润滑效果对轴承温度的影响最大，剩下依次是轴箱径向受力、轴向受力，并且可以得知轴承的早期表面破坏对轴承温度的影响很小。

4 轴承温度实验验证

以上通过热网络法及有限元仿真2种方法对高速列车轴箱轴承温度场进行了研究分析，以下再结合轴承温度实验探究温度分布情况，验证上述分析结论是否正确。文献[10]仅从振动的角度设计搭建了轴承故障诊断试验台，本文所设计搭建的轨道车辆轴箱轴承试验机增加了轴承温度方面的测试功能，试验台见图4(a)。实验对象为SKF生产的TBU-BT2-8545-AD型双列圆锥滚子轴承见图4(b)，温度测量设备采用由大连交通大学崔云先教授研制的“轨道车辆轴承专用瞬态温度薄膜传感器”，见图4(c)，满足轴承温度实验的测试范围及精度要求，温度测试试验平台见图4(d)。

共选取3组工况进行实验分析，各组工况相关参数见表7。

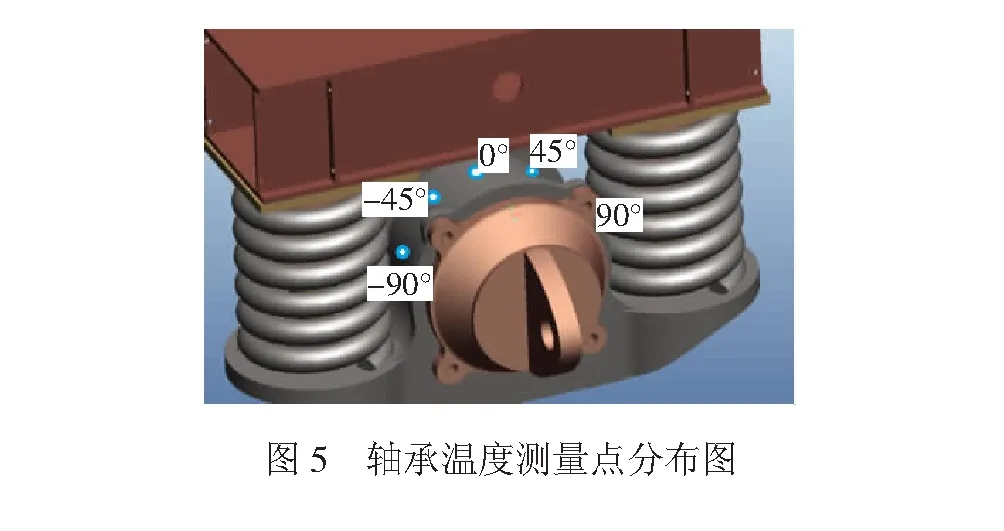
在轴承实验台的轴箱箱体上合理布置温度测点，共布置5个测点，即0°、±45°、±90°各一个测点，测点分布见图5。当轴承运转时，定时对各个测点的温度值进行采集，采样频率为1次/min，采样时间为20 min，结果见图6。

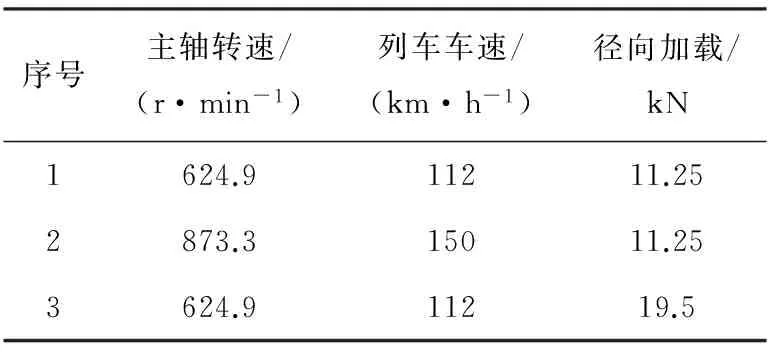
表7 温度实验工况表

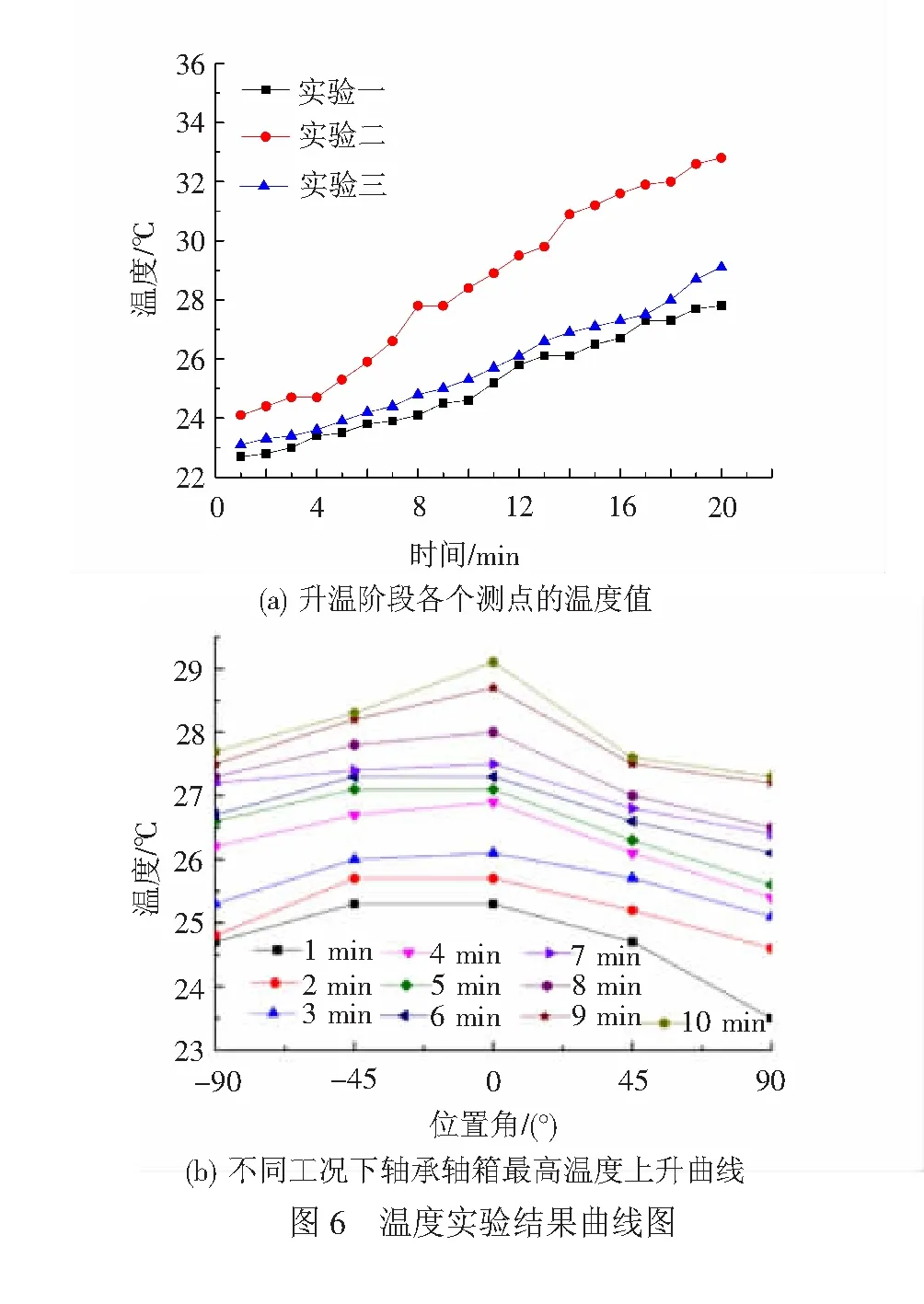
通过图6(a)可以看出，随着转速和径向力的升高，轴承的温度也是随之升高的，由升温过程中的温度值曲线可以观测出，转速升高后温度的上升量明显比径向力提高引起的温升要大，继而得出转速变化对轴承温度的影响比径向力变化对温度的影响大。通过图6(b)可以看出，不同时刻下5个测点的温度值，最大温度出现在位置角为0°的部位，并且随着位置角的不断增大，温度随之降低，并且整体上呈堆成分布，该曲线图验证了有限元及热理论得出的结果——轴承温度整体呈“上高下底”分布，且最高温度出现在轴承外圈最上端。由于实验所测温度为轴箱温度，总体温度值比仿真及有限元仿真值低，并且轴箱传热途径多，使得各个位置温度差异不是特别明显，但还是可以得出轴承温度分布的规律。

通过对国内某机车厂的高速列车轴箱轴承进行调研，发现CRH3、CRH5用轴箱轴承均由SKF和FAG厂家生产。在车辆检修时发现由于温度引起的轴承损坏占全部轴承损坏的30%。图7为轴承由于温度原因引起的失效，图7(a)为FAG轴承，图7(b)为SKF轴承。由图可观测出轴承产生烧伤的部位为外圈上，并且通过现场对轴承的拆卸，发现该轴承的烧伤位置正是在轴承承载区即外圈上半区。事实说明轴承的最高温度点与理论计算仿真结果相符合。

5 结论

通过对高速列车轴箱轴承温度的理论分析计算，且利用热理论—热网络法对轴承温度进行理论计算。通过合理分配热节点，计算热对流及热阻，求解热网络平衡方程，最终解得各热节点温度值，得出轴承最高温度点在轴承最上端的外圈内表面与滚动体接触处。

通过采用ANSYS有限元分析软件，自下而上对轴承进行了三维建模，并通过定义接触保证热量传递准确性，从宏观的角度反映出轴承温度的分布情况。温度径向方向呈“上高下低”趋势分布，轴向方向由于轴向力分布不同，表现出双列轴承轴向方向有明显温度梯度。

设计并搭建了高速列车轴箱轴承温度实验平台，根据实验条件合理布置温度测点位置，建立正交试验对影响轴承温度进行分组分析。对不同工况下轴温进行采集分析，试验结果显示轴承温度的分布与仿真及理论计算结果相对应，并且验证了正交实验中转速和径向力对温度的影响程度，证明利用有限元方法研究轴承温度的可行性。借助极差的判断标准对影响因素进行了评判，确定影响轴承温度的最大因素是轴承润滑，其次是径向受力、轴向力，再次是轴承早期的表面损伤。为高铁轴承在线故障检测提供了理论及试验依据，并且为研究轴承散热提供一定的技术支撑。

参考文献：

[1] 刘喆,王燕霜.滚动轴承温度场研究的现状和展望[J].机械传动,2010,34(3):88-91.

LIU Zhe,WANG Yanshuang. Current Situation and Expectation of Research on Temperature Field for Rolling Bearing[J].Journal of Mechanical Transmission，2010，34(3):88-91.

[2] 周素霞,杨月,谢基龙.高速列车制动盘瞬态温度和热应力分布仿真分析[J].机械工程学报,2011,47(22):126-131.

ZHOU Suxia,YANG Yue,XIE Jilong. Analysis of Transient Temperature and Thermal Stress Distribution on the High-speed Strain Brake Disk by Simulation[J].Journal of Mechanical Engineering，2011,47(22):126-131.

[3] 涂亦虓.直升机主减速器系统热分析[D].南京:南京航空航天大学，2012:2-5.

[4] 黄飞,马希直.基于热网络法的行星减速器温度场研究[J].机械传动,2011,35(4):19-22.

HUANG Fei, MA Xizhi. Study on Temperature Field of Planetary Reduction Gear Based on Thermal Network[J].Journal of Mechanical Transmission，2011,35(4):19-22.

[5] 刘志全,张鹏顺,沈允文.高速圆柱滚子轴承的热分析模型[J].机械科学与技术，1997,16(4):607-611.

LIU Zhiquan， ZHANG Pengshun， SHEN Yunwen. Thermal Analysis Models of High Speed Cylindrical Roller Bearing[J].Mechancal Science and Technology，1997,16(4):607-611.

[6] GU Tao. Bearing Basic Konwledge Training[M]. Beijing: SKF China EKC，2009:70-85.

[7] 王振华.实用轴承手册[M].2版.上海：上海科学技术文献出版社,1996:54-84.

[8] HARRIS T A, KOTZALAS M N.滚动轴承分析：轴承技术的基本概念[M]. 罗继伟,译.北京：机械工业出版社,2009:10.

[9] 刘泽九.滚动轴承应用手册[M].北京：机械工业出版社,2006.

[10] 刘建强,赵治博,章国平,等.地铁车辆转向架轴承故障诊断方法研究[J].铁道学报,2015,37(1):30-36.

LIU Jianqiang,ZHAO Zhibo,ZHANG Guoping,et al. Research on Fault Diagnosis Method for Bogie Bearings of Metro Vehicle[J].Journal of the China Railway Society,2015,37(1):30-36.