从“解决问题”到“问题解决”究竟有多远
王宏 夏永立
一、“问题解决”与“解决问题”的联系与区别
“问题解决”作为数学的课程目标,意味着这个“问题”还没有解决,是课程教学所要达到的目标、结果。而“解决问题”,一方面是指数学课程内容,通过教学活动,这个“问题”将要被解决;另一方面,“解决问题”还包含着解决问题的方法、过程。因此,“问题解决”与“解决问题”,既是课程目标与课程内容的关系,又是课程目标与解决问题方法、过程的关系。
“解决问题”和“应用题”同属于课程内容。“应用题”多数是以文字形式呈现的,条件和问题刚好匹配的题目,学生解题时不需要自己去收集信息、发现问题和提出问题。部分学生只根据个别关键字词来掌握题型,根据题型套解题公式,学生善于解决与例题相同的问题,不会解决变式问题和生活中的现实问题,更不会发现和提出问题。
“问题解决”不等同于解答应用题,比之更为宽泛,价值取向也发生了变化。学生在解题的过程中,需要从纷繁的生活信息中比较、分析、筛选出有用的信息,抽象出数学问题,进而解决问题。解决问题的方法不是统一的,有时答案也不是唯一的。这里提及的问题并不是数学习题那类专门为复习和训练设计的问题,也不是仅仅依靠记忆题型和套用公式去解决的问题。
二、基于“问题解决”课程目标下“解决问题”的教学达成
1.创新形式,呈现问题。课程目标的变化带来了教材内容的变化。问题融入各知识领域,独立设置“综合与应用”内容领域,北师大版教材把“数学与生活”“数学与环境”“数学与体育”等引入教材;安排“探索规律”“解决问题策略”专题,苏教版教材出现了“解决问题的策略”“找规律”,增加思考性选学材料;人教版教材里有“数学广角”等。教材的变化就意味着教师的教学也要跟着改变,教师给学生呈现的问题侧重于与现实问题联系密切,非常规、探究性、开放性的问题。要创新问题呈现的形式,问题要具有开放性、趣味性、挑战性。学生在解决问题的过程中,没有现成的类型和解法来套用,需要学生运用所学知识,并通过个人或小组合作的形式探索和实践来解决,具有挑战性。(1)问题的一般解。(代数化:如“打电话”中用t表示时间,n表示人数,找出n与t的关系。)(2)探求问题的一般解的过程与小结。①你是如何寻求一般解的?②解决问题的关键是什么?③问题是何种数学模型,解决它用到了哪些数学知识,用到了怎样的思维方法和数学方法?(3)问题拓展研究。①有没有其他解法?如果有,比较不同解法的联系与差异。②问题推广:如问题中将“每分钟通知1人”改为“每分钟通知2人”……相应的解。(4)应用:类似问题,即相同的数学模型还有哪些实际背景?列出相关问题。这里,问题能不能解决也许并不那么重要,重要的是学生在解决问题的过程中,完成认识上的两个转化。第一个转化,从纷乱的实际问题中,收集、观察、比较、筛选有用的信息,抽象成数学问题。第二个转化是根据已抽象出来的数学问题,分析其中的数量关系,列出解决问题的算式,求出问题的答案。
2.扬长避短,借鉴经验。应用题教学的历史悠久,广大一线教师和许多专家学者在实践和研究中,对应用题教学做了大量有益的探索与改革,总结积累了许多宝贵的经验,对此,教师应有清醒的认识,扬长避短,合理地坚持和继承。传统应用题的审题、分析数量关系、制定解题步骤等都是需要借鉴的。教材及问题解决呈现形式的变化带来了学生读审题目的变化。学生学习数学的过程都不同程度地体现“问题解决”的过程,应用题学习是实现“问题解决”目标的重要载体。传统应用题中一直被社会抨击的—个练习:
有一个水池,打开进水管注满水池要4小时,打开出水管放完整池水要3小时,现在同时打开进水管和出水管,要多少时间才能把一池水放完?
大家指出此题的种种不是:虚拟情境、资源浪费等,从而对传统数学教学提出了质疑。但是我觉得练习和情境只是一个载体,教学是要去理解练习背后的数学思维方式。类似上述的情境如:家庭的收入与支出;公共场所人员的进场与出场;草场里草的生长与割去;人体的新陈代谢、社会人口的增减等,这是一个动态平衡的问题,难道不值得我们去研究?教师可以根据社会和人类的发展适当地调整练习的情境,改变“一个例题一种类型”的“散点式”学习,注重从多种情境中抽象概括数量关系结构,形成数学模型。教师在进行解决问题教学时,或许答案并不重要,重要的是学生在解决问题的过程中想到了什么。如“鸡兔同笼”问题,它只是一个载体,教师要研究在它们身上附着的东西,那就是数学的思想和数学的思考方法。
3.过程为体,策略为用。小学阶段重视解题策略的感悟和思想的渗透,是问题解决教学的重要特征,也是超越传统应用题教学的标志。小学数学中常见的策略有:画图、列表、列举、转化(化归)、假设等。
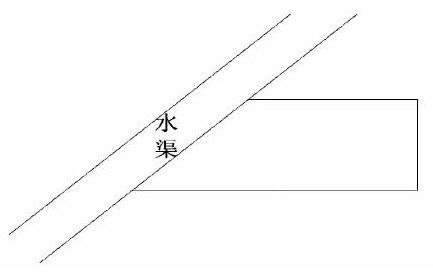
例如:在一边靠水渠处,用篱笆围成一个直角梯形菜地(如下图),已知三面篱笆总长14米,且每面的篱笆长都是整米数。
(1)请试着设计几种围篱笆的方案,并分别求出这块菜地的面积。(至少写出三种方案)
(2)篱笆怎样围时这块菜地的面积最大,最大的面积是多少?
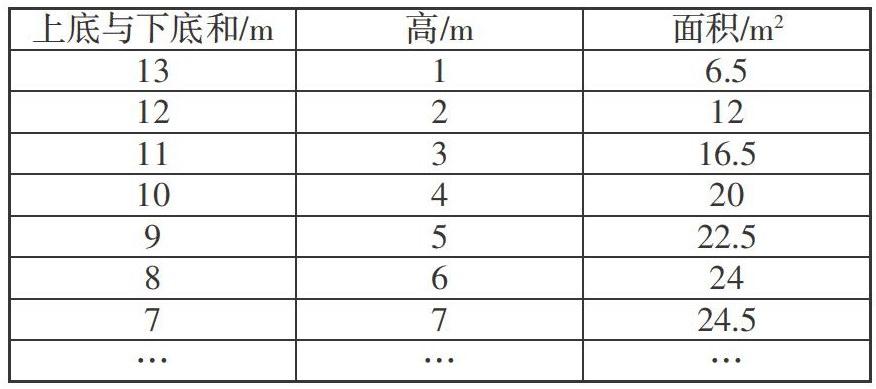
由于问题的探索具有开放性和挑战性,学生需要猜想与尝试,逐步找出答案,发现规律。教师应引导学生利用列表的策略进行有序思考,可以使得问题迎刃而解。
通过列表尝试逐步发现高为7米,上底和下底的和为7米时,这块菜地的面积最大,最大面积为24.5平方米。如(7+7)×2=24.5(m)。学生在解决问题时,就会思考如何有序、不遗漏地计算出一共多少种不同的方法?学生在尝试解决类似问题的过程中,升华了对策略的感悟。
4.学会思考,鼓励质疑。
新课标指出:学生自己发现和提出问题是创新的基础;独立思考、学会思考是创新的核心。培养学生的问题意识和创新意识不是一朝一夕可以完成的事情,教师要通过示范、指导、评价等多种途径促进学生的问题意识。
(1)纵向思维,由浅入深。
如,教学“三角形内角和”时,教师可以提出:三角形内角和是180°,那么四边形、n边形的内角和是多少度呢?三角形、四边形、n边形的外角和是多少度呢?三角形的内角和一定是180°吗?或许学生探究不出结论,但是在学生心中种下了问题的种子。纵向思维体现特殊到一般,由一元到多元、由低维到高维的过程。
(2)横向思维,由此及彼。横向思维体现在由一种数联想到另一种数、由一种运算联想另一种运算、由一种图形联想到另一种图形的思维过程。
例如:数线段的条数,学生掌握了基本的方法。可以尝试解决下面的问题:
然后再让学生尝试解决下面的问题:下图中一共有多少个角?
(3)逆向思维,因果倒置。逆向思维就是对结论进行逆向的质疑。
如:计算3个五角硬币和5个一元硬币的总币值是多少?可以提出问题:6元5角还可以由哪些硬币组成?
5.积极评价,提倡反思。评价既要关注学生学习的结果,也要重视学习的过程;既要关注学生数学学习的水平,也要重视学生在数学活动中所表现出来的情感与态度,帮助学生认识自我、建立信心。
如:用长24厘米的细绳围成一个边长为整厘米数的长方形,怎样才能使面积最大?
在评价时可以关注几个不同的层次:(1)能理解题目的意思。(2)能否提出解决问题的策略。(3)能否列举出若干满足条件的长方形,并能有序排列。(4)在观察比较的基础上能否发现其中的规律并能提出猜想。(5)能对猜测的结果进行验证。(6)进一步思考:边长如果不是整厘米数情况怎样?
“问题解决”作为数学教学的重要方面2-,如何更好地进行教学,达成目标,使学生学会用数学的眼光观察世界,发现问题和提出问题,学会用数学的思想方法分析和解决问题,是广大数学教师需要共同努力去研究探索的课题。
责任编辑:徐新亮

