数字电路中卡诺图的灵活应用

刘玲

摘要：卡诺图是一种体现逻辑相邻关系的几何图形，多用于逻辑函数的表示和化简。通过实例，展示了卡诺图在求解逻辑函数的反函数、判断竞争冒险现象以及组合逻辑电路和时序逻辑电路设计中的应用。灵活运用卡诺图，将大大简化数字电路的分析和设计过程，起到事半功倍的效果。

关键词：卡诺图 数字电路 逻辑函数 应用

中图分类号：TN79 文献标识码：A 文章编号：1007-9416（2016）05-0000-00

Abstract：Karnaugh map is a kind of geometric figure that reflects the relation between the adjacent， which is used in the representation and simplification of logic function. Though a number of examples， it shows the application of karnaugh map such as solving the inverse function of logic function， judging the phenomenon of competitive adventure and the design of combinational logic circuit and sequential logic circuit . It can greatly simplify the process of analysis and design of digital circuit by flexibly applying karnaugh map， which can have a great effect.

keywords：karnaugh map； digital circuit； logic function； application

1 引言

卡诺图是由2n个方格组成的、并能体现最小项逻辑相邻关系的几何图形。从卡诺图上能直观地找出具有相邻关系的最小项并将其合并化简，这种方法无需特殊的技巧和熟记公式，只要按照正确的步骤和一定的化简原则就能容易地得到最简结果，因此卡诺图在逻辑函数化简中得以广泛的应用。

事实上，卡诺图除了可以化简逻辑函数，还有很多其他的用途，只要灵活运用，即可大大化简数字电路的分析和设计过程。本文通过实例，阐述了卡诺图在逻辑函数化简之外的几点巧妙应用。

2 卡诺图在数字电路中的巧妙应用

2.1利用卡诺图求逻辑函数的反函数

利用反演规则可以比较容易地求出逻辑函数的反函数，但得到的表达式并一定最简。如果利用卡诺图，对逻辑函数表达式中没有出现的最小项之和进行化简，即采用包围0的方法，得到的表达式即为逻辑函数反函数的最简与或式。

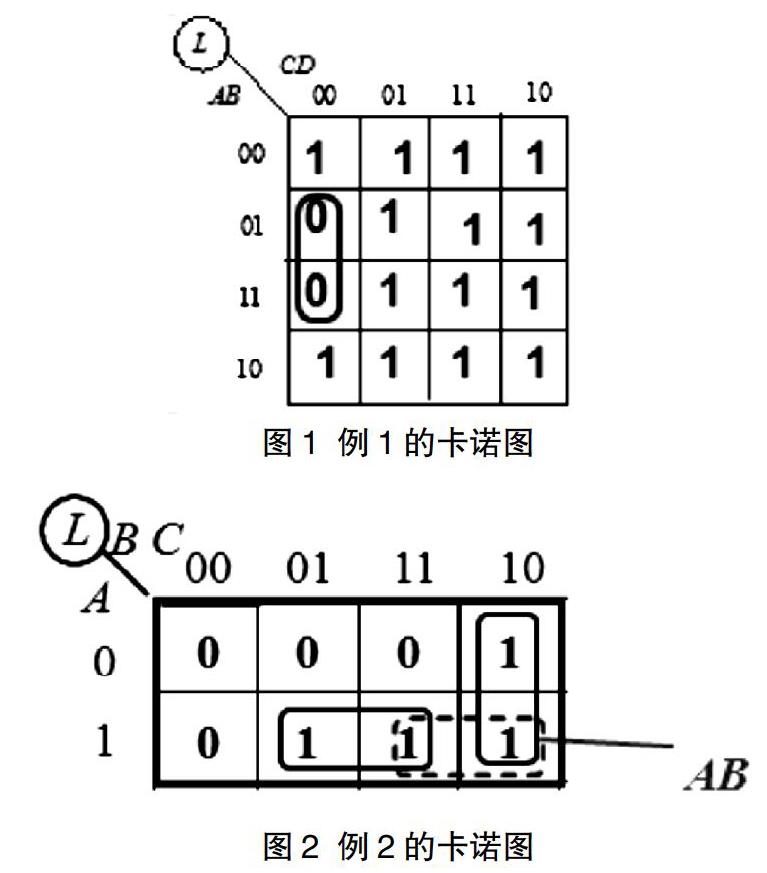
例1：求逻辑函数的反函数。

解：画出逻辑函数的卡诺图（如图1），在卡诺图中对0加包围圈，可求出反函数的最简与或式，即得。

2.2利用卡诺图分析组合逻辑电路中的竞争冒险

在组合逻辑电路中，门电路的两个不同电平输入信号同时向相反方向转换的现象称为竞争，由竞争而可能产生输出干扰脉冲的现象称为冒险。为保证电路正常工作，设计时需注意判断和消除竞争冒险现象。判断和消除竞争冒险的方法有代数法、实验室法，其中利用卡诺图判断有无竞争冒险，并用增加冗余项消去互补变量的方法，直观、简便。

卡诺图法的步骤是：先画出逻辑函数的卡诺图，然后在卡诺图上画出与表达式中的乘积项相对应的包围圈，如果圈与圈之间出现相切，且相切处没有被其他圈包围，即可判断出现竞争冒险现象。

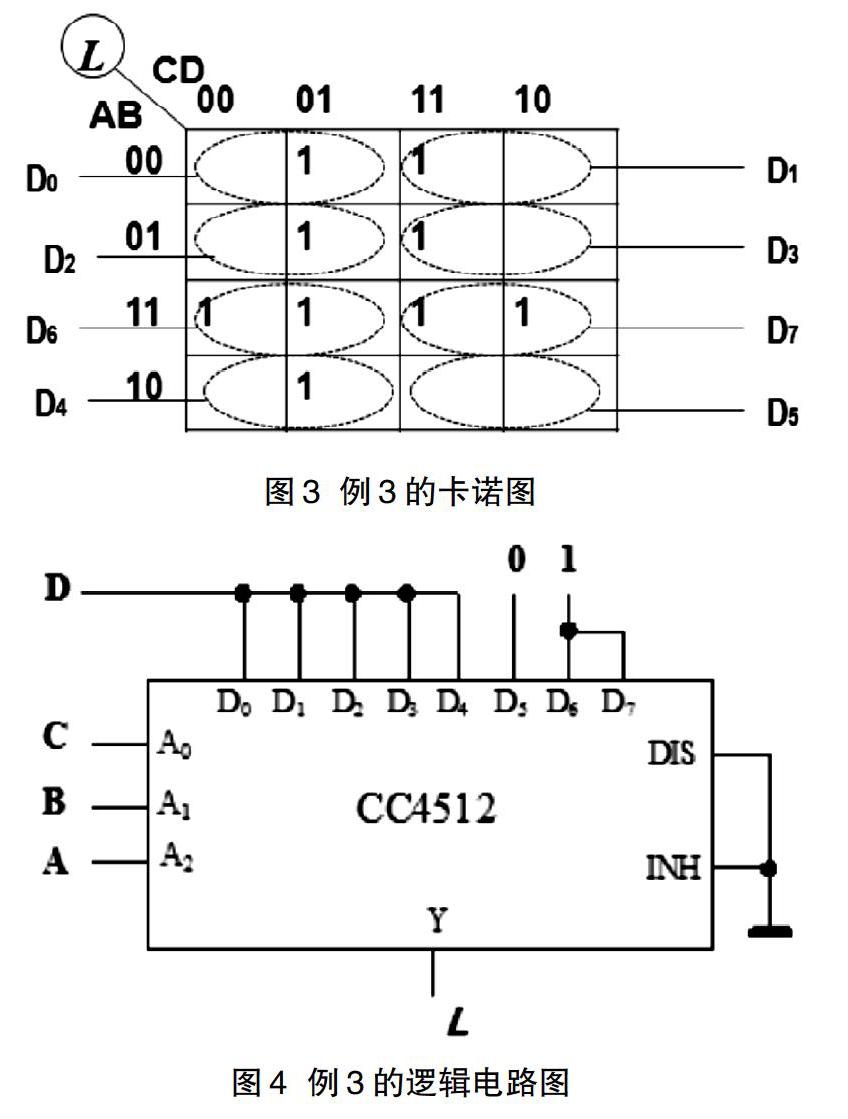
例2：判断逻辑函数是否有可能产生竞争冒险，如果可能应如何消除。

解：由逻辑函数画出卡诺图（图2），并按、画出包围圈（图2上用实线表示），从图上可看出两个圈相切，且相切处没有被其他圈包围，表明产生了竞争冒险，此时，若对相切部分的相邻项加包围圈（图2上用虚线表示），即增加冗余项，从而实现竞争冒险现象的消除。此时逻辑函数的表达式变为。

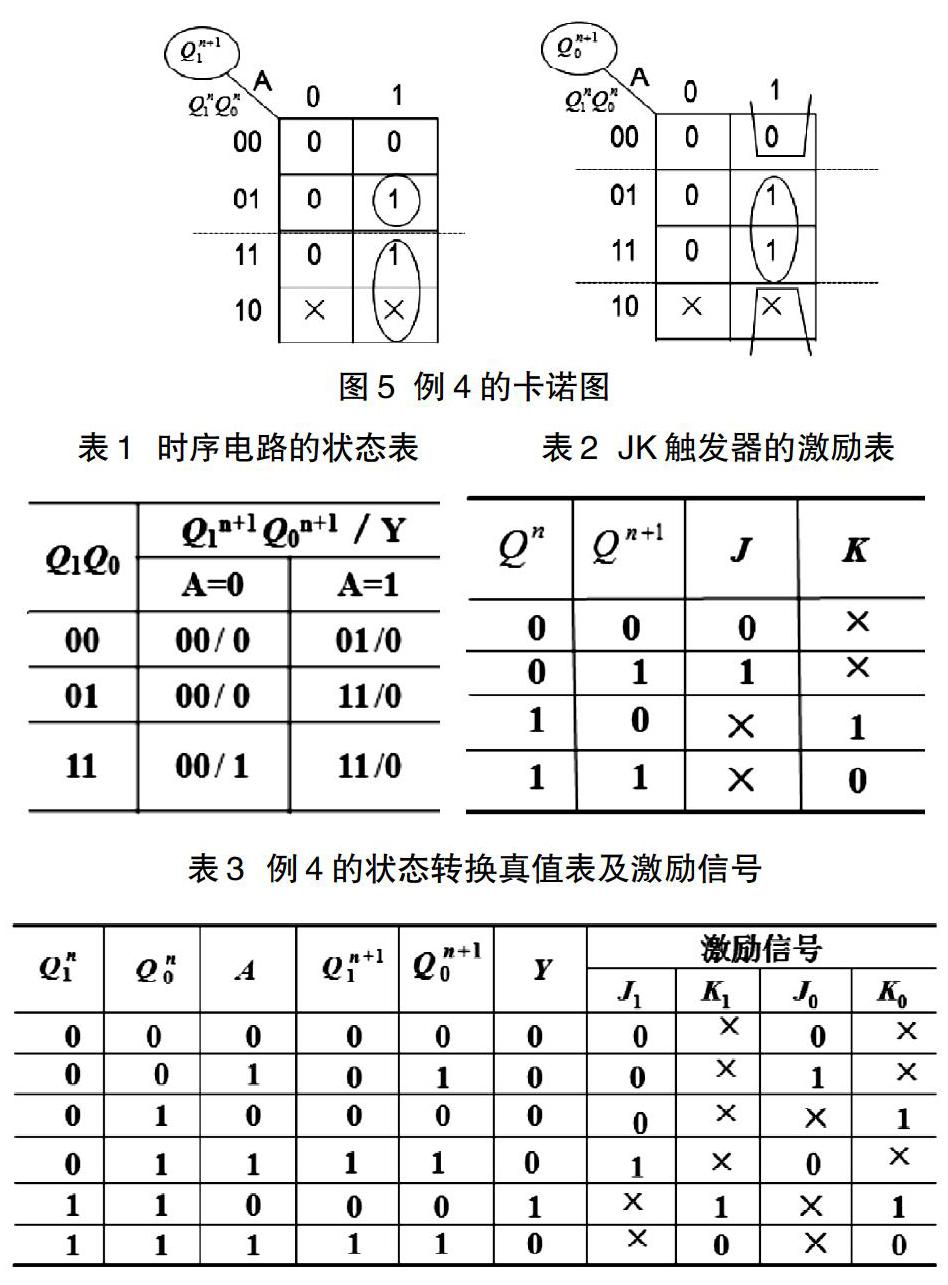
2.3利用卡诺图实现“用具有n 个地址输入端的数据选择器设计m变量（n

用具有n 个地址输入端的数据选择器设计m变量（n

卡诺图法步骤是：先画出逻辑函数的卡诺图，然后选定地址变量，并以地址变量的变化组合在卡诺图上画包围圈，再根据包围圈中出现1的方格写出除地址变量外的变量形式，该变量形式即为数据数据端的输入量Di。

例3：用8选1数据选择器CC4512实现逻辑函数。

解：画出逻辑函数的卡诺图（图3），选地址A2A1A0变量为ABC，即把ABC接在器件的地址输入端A2A1A0。然后在卡诺图上以ABC的八种取值组合画包围圈（用虚线圈表示），由每个包围圈中出现1的方格，可得数据输入端分别为：，，，按此结果可画出相应的逻辑电路图（图4）。

2.4利用卡诺图实现“用JK触发器设计时序逻辑电路”

时序逻辑电路设计步骤一般是先根据逻辑功能确定欲实现电路的状态表，再选定触发器类型，然后求取输出方程和触发器的激励方程，最后进行自启动检查，画出逻辑图。若选择JK触发器，电路的激励方程需要间接导出。借助卡诺图可快速容易地求出JK触发器的激励方程。

例4：已知某时序电路的状态表如表1所示，用JK触发器实现该电路。

传统方法：结合时序电路的状态表（表1）和JK触发器激励表（表2）可得表3，据此画出两个JK触发器的输入J、K和电路输出Y共计5个卡诺图。然后遵循卡诺图化简原则即可找到触发器的激励方程和输出方程。这种方法要求能准确写出JK触发器激励表，而且卡诺图使用个数较多。

巧妙方法：直接根据表1画出次态卡诺图（图5），在卡诺图上按变量Q1取值为1、为0把卡诺图分成两部分（用虚线划分），并在每个部分对出现1的格子画包围圈，根据每个包围圈写出与项式并相加得到次态表达式，与JK触发器的激励方程对比，则很容易地得到触发器1的激励方程，同样的方法可得到触发器0的激励方程。

3 结语

综上所述，卡诺图在数字电路中应用广泛，不仅可以化简逻辑函数，还可以在求逻辑函数的反函数、组合电路中竞争冒险判定、组合逻辑电路设计、时序逻辑电路设计等方面体现其优越性。灵活巧妙地运用卡诺图，对提高数字电路课程的教学效果和简化数字电路的分析设计过程，都起到了事半功倍的效果。

参考文献

[1]康华光 主编.电子技术基础数字部分（第五版）[M].高等教育出版社，2006.

[2]江晓安 主编.数字电子技术（第四版）[M].西安电子科技大学出版社，2015.