不等式中再有理数中的九中应用

左效平

在有理数的学习中，不等式有九种重要的应用，让我们跟着左老师一起梳理一下吧。

1.用不等式表示数.

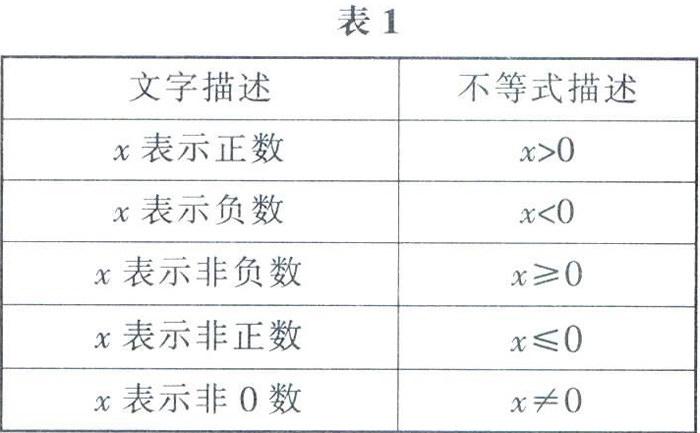
用字母X表示有理数，通过不等号连接有理数X与0，这样就完成了数与不等式的完美对接，如表lI

2.借助数轴，用不等式表示数的顺序.数轴是数学学习的一个重要的直观工具，它的原点对应着数0，右边的点表示正数，左边的点表示负数.根据数轴上右边的点表示的数大于左边的点表示的数，我们就可以利用不等式把一组数按照大小要求排列起来.

例1在数轴上表示出下列各数。并用“<”把它们连接起来.

解：把各数在数轴上表示出来，如图1，根据数轴上右边的点表示的数大于左边的点表示的数，把各数用“<”连接如下： 3.绝对值的化简与不等式. 绝对值的化简也离不开不等式.化简时，需要明确被化简对象的正负。否则得到的结果很难保证正确.

例2实数a、b、c的对应点在数轴上的位置如图2所示，则化简代数式lal-la+b1+Ic-al+1b-cl得到（

）.

A.-a

B.2a-2b

C.2c-a

D.a

4.数轴与不等式.

例3有理数m、n在数轴上的对应点如下页图3所示，则下列不等式成立的是（

）.