电力通信网双通道故障规避算法

杨阳 汪玉成 刘智威 占永红

[摘要]针对传统电力通信网规划算法存在线路过度冗余的问题，论文重点研究电力通信网的双通道故障保护方法，设计了启发式优化算法，有效控制冗余线路的数量和建设成本，并通过实例对算法有效性进行了验证，结果表明本文所提算法具有较高的理论和应用价值。首先，论文分析了双通道故障可能出现的情况，在此基础上建立问题模型；随后，论文将问题转化为整数规划问题，并给出了启发式求解算法；最后，通过实例检验了算法性能，验证了本算法可以防止双通道故障导致的电力通信业务中断，并且使用更少线路，有效控制了建设成本。

[关键词]电力通信网；双通道故障；整数规划

[中图分类号]TP393 [文献标识码]A

1 引言

随着智能电网的快速发展。电力系统间的协同通信日渐频繁，大量电力通信业务部署在电力通信网上，电网的稳定运行对电力通信网可靠性的依赖不断增大㈣。电力通信部门为了提升电力通信网的可靠性，为网络中的每个节点和每条线路建设了多个冗余备份，用以在故障出现时，确保电力通信业务能够及时切换到其保护通道之上，避免业务发生中断，进而不影响电力系统的稳定运行。

然而，随着电力通信网规模的不断扩大，网络拓扑结构也更加复杂。每建设一条线路，就需要不断的增加大量冗余资源来避免双通道故障造成的电力通信业务中断问题，导致网络建设成本过大，难以负担。针对上述问题，本文设计了一种电力通信网双通道故障规避算法，能够大幅减少冗余资源数量，具有重要的应用价值。

在电力通信网规划过程中，如何使网络拓扑结构能够满足抗双通道故障的条件是电力通信部门的重要工作，同时也是电力通信业务的重要指标。本文重点研究电力通信网结构抗双通道故障的相关理论，建立了该优化问题的数学模型，并设计了相应求解算法。最后，利用实例对本算法的有效性进行了验证。

2 问题模型

设传输网拓扑为图G（V，E），V是节点集合（代表传输设备集合），E是路径集合（代表业务通道途径的路径集合）。F（e_F1、e_F2）为双业务通道同时故障的路径对集合，其中，e_F1，e_F2∈F，F为业务通道故障的路径集合。

本文意在图G中建立一个保护结构G（V_P、E_P），其中V_P是节点集合（代表传输设备集合），E_P是路径集合（代表业务通道途径的路径集合）。图G（V_P、E_P）中的业务在发生双业务通道同时故障后，仍不发生中断，并且减少业务通道所需的路径数，即减少冗余网络资源数量。下面通过1个实例具体说明本文所研究的问题。

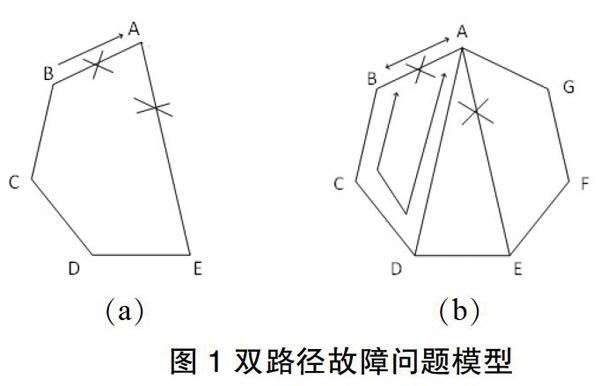
如图1所示中的电力通信网拓扑结构为G（V、E），节点A，B，C，D，E，F，G∈G（V，E），边E_AB，E_BC，E_CD，E_DE，E_EF，E_FG，E_AG，E_AD，E_AE∈E。在图1（a）中，对于顶点A，有1条业务的通道：B←→A，其保护通道为：A←→E←→D←→C←→B。如果这两条通道同时故障，这时A与B之间没有其他线路可选，业务就会发生中断。而在图1（b）中，还存在A←→D←→C←→B这条线路，在节点A发生双通道故障时，仍能保持通信，网络结构更应该设计为图1（b）这种结构。但是，对于抗双通道故障来讲，A←→G←→E←→F←→D←→C←→B这条线路就属于过度冗余资源，存在浪费，应避免这种情况的发生。为此，本文设计了相应的算法解决这类问题，下面对这部分内容进行详细介绍。

3 电力通信网双通道故障规避算法

设传输网拓扑为图G（V、E），V是节点集合（代表传输设备集合），E是路径集合（代表业务通道途径的路径集合）。F（e_F1、e_F2）为双业务通道同时故障的路径对集合，其中，e_F1，e_F2∈F，F为业务通道故障的路径集合。

本文意在图G中建立一个保护结构G（V_P、E_P），其中V_P是节点集合（代表传输设备集合），E_P是路径集合（代表业务通道途径的路径集合）。图G（V_P、E_P）中的业务在发生双业务通道同时故障后，仍不发生中断，并且减少业务通道所需的路径数，即减少冗余网络资源数量。

设R为G（V_P，E_P）的最大候选环数，i，j为环的序号，i，j∈{0，0，2，…，R-1}，eⁱ_（u，v）∈{0，1}表示通道（u，v）在环i上，即（u，v）∈R_i。

优化目标的含义为：求一个拓扑结构G（V_P，E_P），其中的通道数最少。约束条件的含义为：

第一个约束：表示V_P中任意节点u至少在3个环上，该节点的度d（u）≥3；

第二个约束：表示每条通道路径在一个环上最多出现一次，不存在环路；

第三个约束：表示每条通道路径至少被两个环共用：

第四个约束：表示两个环至多共用一条通道路径。

本文采用分枝定界法求解上述整数线性规划问题。具体步骤：将式（2）整数规划问题称为问题A，将其对应的线性规划问题称为问题B。

解问题B可能得到情况之一：

a.B没有可行解，这时A也没有可行解，则停止；

b.B有最优解，并符合问题A的整数条件，B的最优解即为A的最优解，则停止；

c.B有最优解，但不符合A的整数条件，记它的目标函数值为z。

用观察法找问题A的一个整数可行解x_I={eⁱ_（u，v）|i∈{0，…，R-1}，u∈V，v∈V}，试探，求得其目标函数值，并记作z_o以z^*表示问题A的最优目标函数值：这时有z≤z^*≤z，进行迭代：

步骤一：分枝，在B的最优解中任选一个不符合整数条件的变量x_j，其值为b_j，以[b_j]小于b_j的最大整数。构造两个约束条件：x_j≤<[b_j]和x_j≥[b_j]+1，将这两个约束，分别加入问题B，求两个后继规划问题B₁和B₂。不考虑整数条件求解这两个后继问题。

定界，以每个后继问题为一分枝标明求解的结果，与其它问题的解的结果中，找出最优目标函数值最大者作为新的上界z₀从已符合整数条件的各分支中，找出目标函数值为最大者作为新的下界z，若无作用z不变。

步骤二：比较与剪枝，各分枝的最优目标函数中若有大于z者，则剪掉这枝，即以后不再考虑。若小于z，且不符合整数条件，则重复第一步骤。一直到最后得到z^*=z为止。得最优整数解x^*_j，j=1，…，n。

至此，计算出G（V_P，E_P）的拓扑结构，下面给出求解保护通道路径的算法。

步骤1：遍历e_Fi∈F，找到e_Fi的起始节点s和目的节点d：

步骤2：设临时节点t=s；

步骤3：如果t≠d。从环集合中找出t所在的环集合R_f；否则，转步骤8；

步骤4：如果r_i∈R_f，转步骤5；否则，转步骤7；

步骤5：如果目的节点d在r_i上，则P_i=P_i+节点t和节点d在环r_i的最短路径：

步骤6：t=d；

步骤7：t=t的邻节点：

步骤8：返回P（p₁，p₂）；

P（p₁，p₂）为所求业务通道的路径，本算法的时间复杂度为O（E），Dijkstra算法的时间复杂度为：O（V*IgV+E）。

4 实例验证

对于一个具有11个顶点的网络拓扑，如果采用传统保护方法，将得到如图2所示的拓扑结构，其中包含26条线路。而采用本文所提算法得到的拓扑结构见图3，其中包含17条通道路径，大幅减少了冗余线路的数量，并且该拓扑结构满足在抗双业务通道故障的条件，即在任意两条业务通道同时故障时，电力通信业务不发生中断。

5 结束语

本文有效地解决了电力通信网拓扑结构的规划问题，并通过实例验证了算法的有效性。为将该算法应用到电力通信网规划过程中奠定了基础。本文首先将建立了抗双通道故障问题的数学模型，深入分析了问题的本质；随后，将该问题转化为整数规划问题，并设计了启发式求解算法；最后，通过具体实例进行检验，验证了本算法的有效性。