基于影子长度变化定位的技术研究

摘要:根据"立竿见影"现象及竿影日照图的原理,分析影子的形成原理和影子随时间的变化规律, 根据地球自转与公转原理、三角定律、几何原理建立了影子长度与杆长、地理经度、地理纬度、日期和时间关系的数学模型。根据直杆影子的长度变化规律,通过Matlab编程,运用参数估、拟合等方法来推断直杆所在的地理经纬度。
关键词:影长 参数估计 指定函数拟合 matlab
1 "立竿见影"现象
一根直立的竿,其影子的位置在一天中随太阳的位置不断变化。假设某天某时刻的太阳位置如图1所示,立于地面上的竿高为H,太阳光线通过竿顶P点,在地面上形成一个影子点P′,影子的长度OP′为L,单位为米。定义太阳光线与地面的夹角∠PP′O=β,则其数学关系式为:
=cotβ
上式中β为太阳高度角。
2 直杆影子长度的影响因素分析
根据现有的天文学知识可得如下的影子长度影响因素层次分析图:
太阳的高度角计算:
3 运用参数估计求出直杆所在地的经纬度
有(9)式可知,若已知杆长H,太阳赤纬 ,纬度 ,经度J,则影长L与北京时间T 具有确定的函数关系。而地理的经纬度是未知的,我们将其认定为该函数的未知参数,可以利用 MATLAB 中的 fittype 函数对北京时间 T 与影子长度 L 进行指定函数拟合,得出参数数值,即解得直杆的地理纬度 ,经度 J。
4 计算算例
以2015年高教杯数学建模A题中的数据为例。
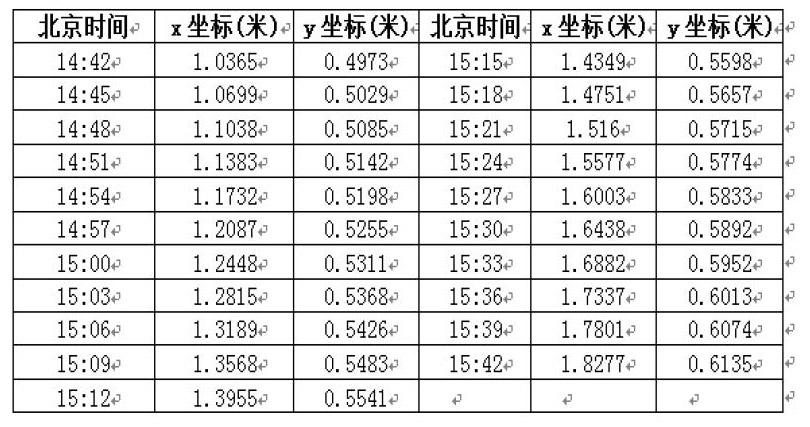
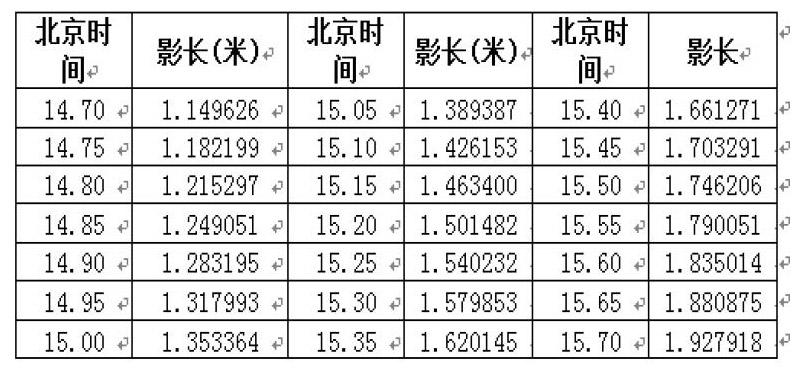
说明:坐标系以直杆底端为原点,水平地面为xy平面。直杆垂直于地面。测量日期:2015年4月18日。
将时间换成以小时为单位以及将x、y坐标换算成影子长度H,如下表。
由4月18日得到积日为108天,年份为2015年,带入(2)、(3)、(4)、(5)中可得到太阳赤纬为10.6305°。
运用MATLAB,编写程序利用fittype函数编写代码,对北京时间与影子长度进行指定函数拟合,得到参数数值,本题中杆长未知,所以也将其作为一个位置参数,运行代码,在95%置信区间,得到以下结果:
杆长 H = 2.034 (2.029, 2.038)
经度 J= 108.7 (108.6, 108.8)
纬度u = 19.29 (19.23, 19.34)
答案中经纬度为(109.5°E, 18.3°N),与通过计算的经纬度误差在1°左右,可以认为该结论可信,而且本题中并没有告诉直杆的长度,多了一个未知参数,若已知杆的长度,误差会缩小,所以可认为本模型合理。
5 结束语
该模型建立了杆的影长与五个因素(经度、纬度、日期、时间、杆长)函数关系表达式,时间为自变量,其它因素为参数,利用参数估计可求解出直杆的经纬度。模型简单准确,但是任有许多不足和可以改进的方向,例如:忽略了大气折光的影响,以及平太阳时和真太阳时之间的差别等。对于这些因素造成的误差还需要进一步研究。
参考文献:
[1] 郑鹏飞,林大钧,刘小羊,吴志庭,基于影子轨迹线反求采光效果的技术研究,华东理工大学学报(自然科学版),第36卷第3期,文章编号:1006-3080(2010)03-0458-06,2010.03:458-463
[2] 汪和平,影子与季节、纬度的关系,中学数学(高中版),2008年第9期
[3] 张文华,司德亮,徐淑通,祁东婷,太阳影子倍率的计算方法及其对光伏阵列布局的影响[J],技术与产品,2011.9:28-30
作者简介:邹宇雄 (-),男,汉族,湖北仙桃人,学生,郑州大学 ,水利水电工程 。

