把握学段目标促进有效衔接

林枫

“图形与几何”是以发展学生的空间观念、几何直观、推理能力为核心的。《义务教育数学课程标准（2011）》中针对这部分内容的编排体现了从生活到数学、从直观到抽象、从局部到整体的特点，且三维、二维、一维图形交替出现，目标要求逐渐提高。在认识同一个或同一类图形时，要求都有明显的层次性：从“直观辨认”到“初步认识”，再从“认识”到“探索并证明”。那么，我们该如何有效实现不同学段教学的有效衔接？本文以“认识平行四边形”的相关教学为例谈一谈具体的做法。

一、了解教材编排特点，准确把握学段要求

学生从对客观物体的观察中逐渐抽象出图形，是一个逐步深化、渐进提高的过程。为此，教材在编排上根据学生的认知能力与年龄特点，以逐步拓展、螺旋上升的结构，把“图形与几何”的内容均衡地安排在不同的学段中，每一学段都有相应的达成目标，这样，既注意前后连贯，又能突出每个年级的学习重点，分散难点。“认识平行四边形”这一内容，在小学阶段分为直观辨认和概念学习两个阶段进行编排：第一阶段安排在一年级，仅要求学生能够直观认识平行四边形，能从具体的实物或图形中辨认出哪些是平行四边形，对平行四边形的一些特点有初步的直观感性认识；第二阶段则安排在四年级，以“两组对边分别平行的四边形叫作平行四边形”内涵定义法，对平行四边形加以理性认识。教师要认真研读，理解教材的编排意图，准确把握不同学段的教学目标，关注知识的过渡与衔接，以免出现盲目拔高或降低要求的现象。

二、立足学生原有经验，合理展开教学活动

学习的起点是弄清学生已经知道了什么，新知的建构往往是通过新旧知识的衔接来完成的。成功地实现原知与新知的衔接不仅可以激发学生的学习兴趣，降低学习的坡度，而且有利于学生对知识的整体认知与建构。

考虑到在一年级下学期，学生对平行四边形的基本特征有了初步的感受，该部分的教学笔者立足于学生已有的知识基础，以“你身边哪些物体的面是你认识的平行四边形”问题为起始，结合教材中的实物图片，引导学生抽象出位置、方向、大小都不同的平行四边形图形，由此激活学生已有的知识储备，扫除新知带来的距离感，为学生对平行四边形的认识从感性到理性铺好路径，从而实现知识间的学段衔接。

三、遵循学生认知特点，经历有效探究过程

“图形与几何”领域的知识，对于小学生来讲，无论是线、面、体的特征还是具体某一图形的特点，都是比较抽象的。但正如波利亚所言：要用一切办法使它们看得见，摸得着。《课程标准》中较多地使用“通过实物和具体模型，了解……”“结合实例（生活情境）了解……”“通过观察、操作、认识……”等句式表述教学要求。相关教材内容更是在积累大量直观、感性材料的同时，通过活动化的形式呈现，如拼一拼、摆一摆、折一折、比一比等。实际上这些措施都明确了认识图形的过程和方式，生活经验、情境描述、观察实物、动手操作、几何抽象等都是培养和发展学生几何直观、空间观念的重要途径。

例如，“认识平行四边形”的相关知识在一年级教学时的学习活动可以作如下安排与设置。

认一认：认识藏在物体上的平行四边形，初步感知图形的特点。

想一想：怎样把手中物体上的图形请到纸上？

画一画：根据自己的想法，把物体上的图形拓印到纸上。

围一围：利用4颗钉子你能围出多少种不同形状的平行四边形？

研一研：仔细观察这些图形，它们的形状、大小各不相同，怎么就都是平行四边形呢？

找一找：周围哪些物体中还藏着是我们刚认识的平行四边形？

“认识平行四边形”的相关知识在四年级教学时学生经历的数学活动可以作如下设置。

回顾：生活中你们见过平行四边形吗？在哪里见过？（抽象出平行四边形）

猜测：这些平行四边形看起来形状、大小不同，但仔细观察，你觉得它们都有哪些相同的地方？（学生猜测：对边相等，对边平行，对角相等）

验证：每个人手中都有不同的平行四边形，你能想办法动手验证自己的猜想吗？是不是所有的平行四边形都具有这样的特征呢？

交流：你觉得什么样的图形叫作平行四边形？

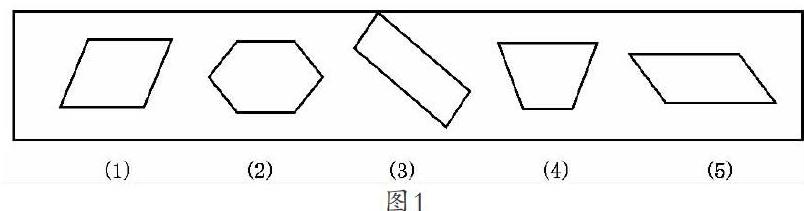
辨析：下面哪些图形（图1）是平行四边形，哪些不是？请说明理由。

这些根据不同学段教学目标精心设计的学习活动，不仅遵循了学生认知从直观感性思维到抽象理性思维的发展，更实现了知识的自然推进与有效衔接。同时，让学生在不同层次的学习中积累下丰富的数学活动经验。

四、深刻理解知识本质，建立知识整体联结

我们要充分认识到数学课程结构阶段性和整体性之间的关系，纵观教材，系统思考。在备课之前的调查时，笔者发现大部分学生都知道“长方形是特殊的平行四边形”，可是当笔者问他们“特殊在哪儿”时，他们的回答大都是：“平行四边形没有出现直角，而长方形的四个角都是直角。”可见，学生对平行四边形的认识仅仅停留在表面，对于两者之间的包含关系并没有真正理解。鉴于此，笔者在教学时，借助基于现代信息技术的多媒体课件的动态演示，将平行四边形和长方形、正方形三者之间的包含关系分两个层次进行深入理清。

第一层次：认识长方形和正方形都是平行四边形。

（1）（课件出示两组平行线）同学们，借助自己的双手，像林老师这样（手势表示）创造一组平行线，再跟同桌的比划一下。

（2）（课件动态演示两组平行线旋转、相交）如果像这样旋转手中的平行线，当它与你同桌手中的平行线相交时，中间会出现什么样的图形呢？先想一想，再与同桌交流、验证。

（3）（课件动态演示五次不同的旋转、相交的情形）同学们，在每次的旋转、相交中出现的四边形，什么变了，什么不变？

（4）师小结：不管四边形发生怎样的变化，只要是这两组平行线相交形成的，两组对边就始终会分别平行，它一定是平行四边形。

第二层次：认识长方形和正方形的特殊性。

（1）（课件演示：两组平行线相交出现直角）请再仔细观察，中间形成的始终是平行四边形，但是跟之前的平行四边形一样吗？

教师引导学生小结：长方形是特殊的平行四边形。

（2）（课件演示：拉近两组平行线之间的距离变成四条边都相等）如果再特殊一点，当四条边的长度都相等时，这个长方形就变成了？

（3）教师引导学生小结：正方形是特殊的长方形，长方形是特殊的平行四边形。（课件展示三者之间的关系集合图）

抓住平行四边形的本质属性，引导学生在变与不变中深刻理解平行四边形、长方形、正方形三者之间的包含与被包含的关系，使学生对平行四边形的认识向纵深发展，也使“认识平行四边形”这部分的知识实现了整体联结。

（作者单位：福建省连江县教师进修学校第二附属小学 本专辑责任编辑：王彬）