FIR滤波器在音频系统优化中的基本应用
Hadi Sumoro 于弦
[摘要]介绍IIR和FIR两种滤波器及其相位响应,重点分析FIR滤波器的特性、处理延时、窗函数处理,以及FIR滤波器在音频系统优化中的基本应用。
[关键词]滤波器;无限脉冲响应;有限脉冲响应;音频系统;频率响应;相位响应;处理延时
文章编号:10.3969/j.issn.1674-8239.2016.08.010
1 滤波器简介
无论是为了补偿扬声器响应的非线性,还是为了改变房间的声学效果,以均衡形式出现的电子校正手段是针对扬声器进行补偿和校正最为有效的工具之一。常用的音频滤波器有两种:IIR和FIR。IIR是无限脉冲响应(Infinite Impulse Response)的缩写,FIR是有限脉冲响应(FiniteImpulse Response)的缩写。这两种滤波器各有优缺点。笔者将对相关术语进行解释,并介绍FIR滤波器在音频系统优化当中的若干基本应用,希望广大音频领域从业者能够从中获得有用的信息。
IIR滤波器是基于无源模拟滤波器的理念来设计的,这种滤波器具有最小相位(Minimum Phase)的特点。图1所展示的是一个扬声器中常见的无源分频设计。IIR滤波器通常被用于模拟无源设计以及数字信号处理器当中。一些与IIR相关(其中也与FIR相关)的术语包括:模拟无源分频、最小相位滤波器、模拟图示/参量均衡。而FIR滤波器则通常出现在数字领域当中。
2 相位响应
IIR滤波器具有最小相位特性,将它的频率响应做希伯特变换(HilbertTransform)可以计算出相位响应,反之亦然。在IIR当中,频率响应的改变会导致相位响应的改变。最小相位响应指的是在一定幅度响应条件下可能产生的最小相移。
图2所示的数字IIR滤波器包含了一个截止频率为60Hz,斜率为12dB/oct的巴特沃兹高通滤波器;一个截止频率为12500Hz,斜率为12dB/oct的巴特沃兹低通滤波器;并且在300Hz以1/3oct宽度衰减3dB,在3000Hz以1/3oct宽度提升3dB。图2为Filter Hose软件的截屏。
从图2中可以观察到传递函数(图3-a)和滤波器的脉冲响应(图3-b)。
图3-a显示了IIR滤波器的频率响应(红色曲线)和相位响应(绿色曲线)。基于前文的讨论,相位会随着幅度的改变而改变,相位响应的走向是其自身特有的,用户不可以对其进行单独的调节控制。图3-b显示了滤波器的脉冲响应,其峰值非常接近于0ms。通常由具有最小相位特征的IIR滤波器所引入的处理延时是非常小的(并不是所有IIR滤波器都是最小相位,全通滤波器就是非最小相位滤波器)。
通过FIR滤波器可以获取一个与图3幅度响应相似的传递函数。图4是一个采样率为48kHz,阶数为1024的FIR滤波器。虽然FIR滤波器可以被设计为最小相位特性,但它强大的功能体现在能够分别控制频率和相位响应。这种滤波器通常也被称为线性相位FIR滤波器。
图4-a显示了滤波器的脉冲响应。如图脉冲峰值位于10.65ms,由此可以判断由滤波器产生的处理延时。换句话说,滤波器的输出将会获得一个10.65ms的额外延时,这对于现场舞台返送或者分期录音来说太长,但对于母带处理或者不含视频内容的音乐欣赏来说则是可以接受的。
图4-b显示了该FIR滤波器的传递函数,该图通过对脉冲响应做周期性移动去除了处理延时,使得图像的相位响应易于观察和对比。可以看到相位响应在0度保持平直(滤波器没有造成任何相位偏移),而频率响应则与图3-a相似。
3 数字FIR滤波器的特性
在数字音频领域,采样率(fs)是用户需要认识的最为重要的限制条件。FIR滤波器的性能取决于硬件或软件的采样率。人们无法在改变滤波器采样率的前提下获得同样的效果。
根据名称可以知道,一个FIR滤波器具有有限(响应)长度,即一定的阶数。FIR的脉冲响应是一个数组,而FIR的阶数则是这个数组的长度。更高的阶数意味着更高的频率精度,进而意味着更窄的滤波器和/或更加陡峭的滚降。然而,阶数往往受限于硬件的内存量和计算能力。
用采样率除以阶数,可以计算出滤波器的频率精度。在图4所示的例子当中,FIR滤波器采样率为48kHz,阶数为1024。因此其频率精度为46.875Hz。针对此数据做快速估算,可以将频率精度乘以3,以此得到滤波器可以作用的频率下限。46.875Hz×3≈141Hz,这意味着具有48kHz采样率、1024阶数的FIR滤波器将会对141Hz以上的频率有效。这仅仅是基于采样率和阶数的粗算,其他计算参数的引入或者对滤波器的修改将会极大地改变最终的结果。
为了在低频区域(低于200Hz)获得一个陡峭的高通滤波器,需要一个很高的阶数,这在实际应用当中是不容易实现的。因此,通常使用一个IIR的高通滤波器作为FIR滤波器的补充。
4 滤波器的处理延时
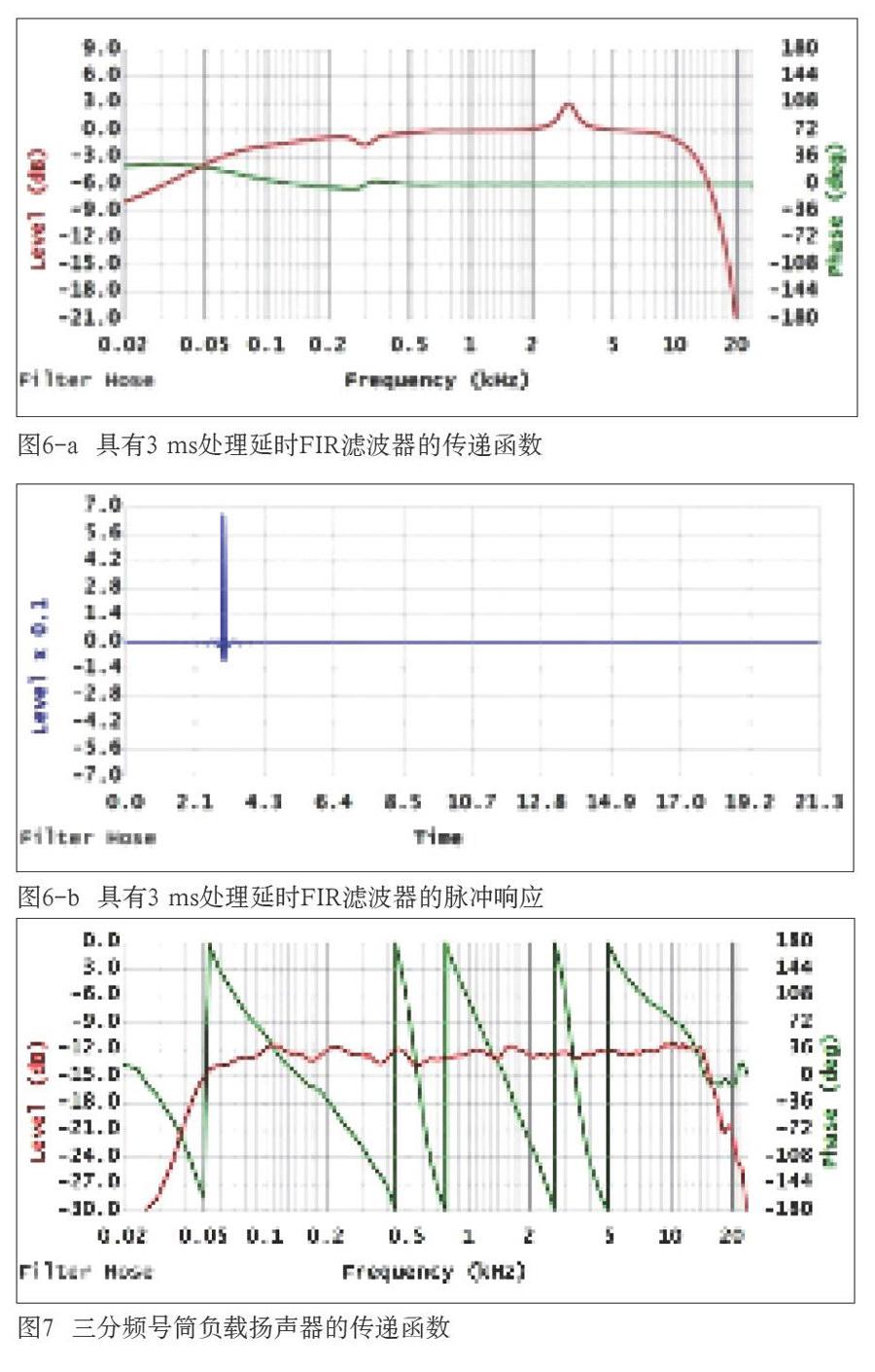
另一个重要的因素是对滤波器进行编辑。图4中显示的FIR滤波器具有10.65ms的处理延时。当滤波器脉冲响应经过周期性移动,并且施加合适的窗函数后,所获得的滤波器的传递函数可能发生改变。请看图5(6ms处理延时)、图6(3ms处理延时),并将它们和图4(10ms处理延时)进行对比。图4、图5、图6当中的相位响应曲线都通过周期性移动将脉冲响应的峰值对齐在0ms,以便于观察和对比相位响应。
可以观察到低频滚降是如何改变的,以及低频区域的相位响应并不如高频区域的相位响应平直。总的来说,如果允许较长处理延时的存在,FIR滤波器可以对100Hz以下的频率进行有效的修正。此外,还有一个关于三分频号筒负载扬声器测试的例子。扬声器的传递函数如图7所示。
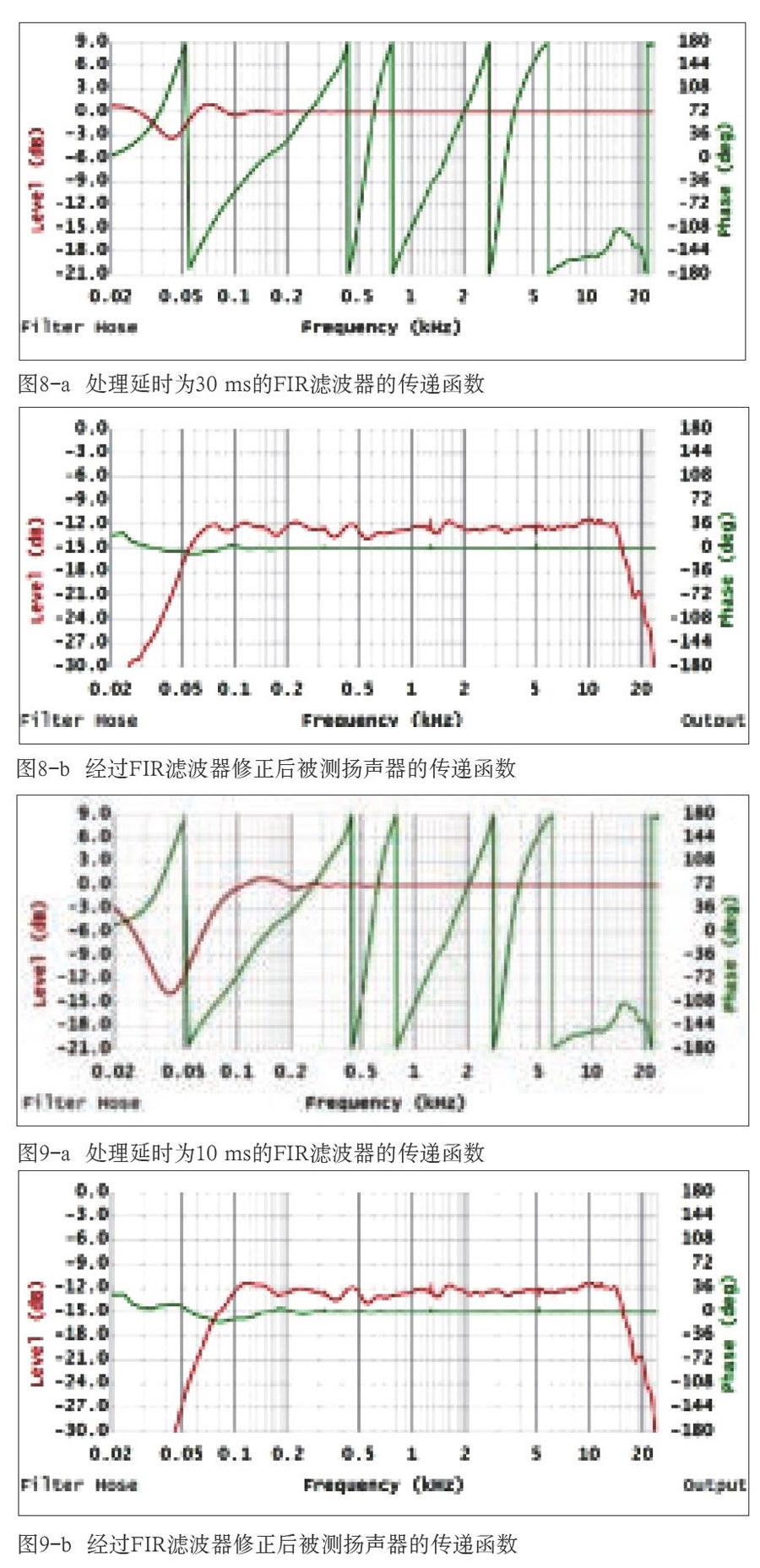
分别使用两个由不同处理延时生成的FIR滤波器(采样率48kHz,阶数Ⅳ=2048,频率精度23.3Hz),仅对扬声器的相位响应做线性修正,不影响其频率响应。图8和图9分别显示了这两个滤波器的传递函数(a图)和修正后的输出情况(b图)。
图8所使用的滤波器具有30ms的处理延时。该滤波器的频率响应除了在45Hz附近有所衰减之外,其余几乎都是平直的。这种设置能够很好地对扬声器系统的相位响应做线性化处理。但是如果将处理延时缩短至10ms,那么得到的结果则会十分不同。
图9-a显示的是具有10ms处理延时的FIR滤波器的传递函数。可以看到它的频率响应在80Hz处开始下降。从图9-b所显示的扬声器经过处理后的结果可以看出,该FIR成功地将相位响应修正得十分平坦,但低频响应却无法保持图7中原始响应所具有的下限。5施加窗函数
从名称就可以知道,FIR具有一个有限长度的脉冲响应。而在制作FIR的过程当中,使用者需要定义这个脉冲响应截止于何处。FIR对于特定频率响应的控制并不擅长(尤其是低频),因为需要缩短FIR滤波器的脉冲(因此它被称为“有限”)。这种缩短脉冲响应的操作被称为“窗函数”。
通常FIR滤波器的计算基于理想滤波器来进行,在此基础上再被缩短。以下举一些关于窗函数处理的例子。
图10显示的是被称为矩形窗的窗函数。它对矩形(窗)内所有数值做等量加权,并在滤波器的末端做突然截止。这种方法会导致信号振荡或对FIR滤波器处理范围之外的声音带来染色。矩形窗适用于某些特定场合,但通过形状较为平缓的锥形窗使得滤波器脉冲响应的边缘变得更加平缓则是更具普遍性的做法。图11所显示的是Hann窗函数。这个窗函数不仅根据需要的长度截掉了脉冲响应的尾巴,还对滤波器的末端进行了锥形化的平缓处理。系数值在尾巴的末端变为0。处理延时和窗函数的设置和编辑处理对于FIR滤波器的最终结果十分重要。
6 基于测量制作FIR滤波器
随着具有FIR功能的DSP愈发广泛的使用,制作一个反转传递函数,或者只反转频率响应,或者只反转相位响应的FIR滤波器变得越来越普遍。包括Filter Hose在内的一些软件可以帮助使用者定义FIR滤波器,它们基于测量数据来制作一个合成滤波器或者用户自定义滤波器(后者通常用于扬声器分频网络或针对某个特定的目标曲线,本文对此不做讨论)。
根据测量的数据来制作FIR滤波器,其频响是测量数据的反转,经过卷积后可以获得平直的响应曲线。以这个为目的的应用有以下几种。
(1)为单一测量点制作反转FIR
对于单一听音点(例如录音棚当中),可以在“甜点”上做单次测量,以该点测量结果制作相应反转传递函数的FIR滤波器。这对于缓解房间声学影响、修正扬声器非线性有着很好的作用。这种滤波器的系数是个很长的数组,但它只针对空间当中具体的一点进行修正。
(2)使功率响应更加平坦
通过在不同听音者位置测量频率响应,可以通过对频率响应做平均处理来得到大致的功率响应。这种测量应针对每只扬声器单独进行,并且在测量点多于3个时,对频率响应做平均才会得到好的结果。做平均只针对振幅响应,而不针对相位响应。这种测量可以只用RTA(实时测量分析)来进行。这也是补偿房间共振特性的有效方法,常用于家庭影院、听音室或公共场合的音频系统优化。
(3)扬声器校正
为了实现对扬声器的正确校正,测量需要在一个受控的声学环境下进行。这里的“受控”指的是进入测量系统的反射声需要得到控制。进行扬声器测量最简单有效的方法是在适宜的天气环境下,在室外或很大的房间内做地面测量。通过将扬声器和测试传声器放置在光滑的反射地面上,可以得到一个很好的测量数据,避免来自地面反射声的破坏性干涉。当使用FIR滤波器对扬声器的相位响应做线性处理时,最好使用在受控环境中得到的测量结果。
(4)综合用途
测量扬声器并且制作FIR滤波器有很多可能性。可以通过室外地面测量的方式对扬声器进行校准,制作一个FIR滤波器对扬声器的近场响应做线性化处理。然后再将扬声器放在特定房间当中,通过多点测量来获得一个功率响应或者房间共振补偿。这两个滤波器可以被卷积或合并。与IIR滤波器的合并相同,具有不同功能的FIR滤波器也可以进行合并。
FIR滤波器的获得方式与IIR有很大的不同。它们都具有一定的优点和缺点,最终得到的效果则取决于滤波器制作者的意图。从本文可以看出,FIR滤波器为音频领域从业者提供了又一个有效的工具。
在此,谨感谢Pat Brown和John Loufik对该领域的深入见解,以及在文章发表前的审阅工作。
(编辑 王芳)