函数模型及其应用
2016-05-14 14:03张金铃谢绍义
高中生学习·高二版 2016年8期
张金铃 谢绍义
函数模型是解决复杂的数学问题的有力工具.然而,要能够对各种问题有准确的判断,并且找到最为合适的函数模型,则需要具备较好的思维能力及数学基础. 对于高中范围内一些常见的函数模型,如一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数模型,以及分段函数模型,要掌握它们各自不同的特性以及它们增长的差异性,并结合实例体会直线上升、指数爆炸、对数增长缓慢等不同函数类型的含义.
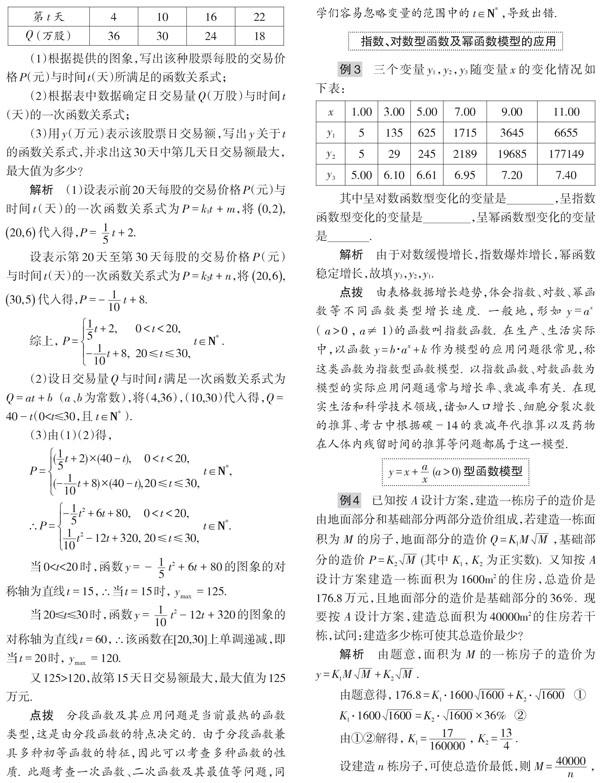
解函数模型及其应用题的一般步骤:(1)审题,弄清题意,分清条件,找准变量,理顺数量关系,初步选择数学模型;(2)建模,将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;(3)求模,求解数学模型,得出数学结论;(4)还原,将数学问题还原为实际意义的问题.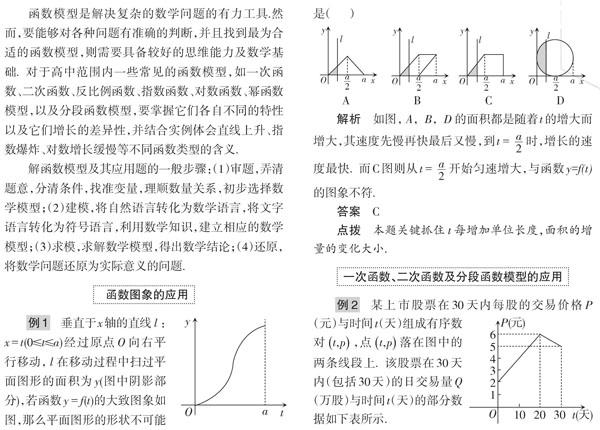

猜你喜欢
体育科技文献通报(2022年3期)2022-05-23
新高考·高二数学(2022年3期)2022-04-29
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2020年9期)2021-01-04
数学大世界(2020年7期)2020-04-25
数理化解题研究(2018年3期)2018-04-02
艺术家(2018年2期)2018-01-24
读与写·中旬刊(2017年10期)2017-10-14
福建中学数学(2016年8期)2016-12-03

