基于全寿命周期成本的配电网规划研究

李小宝

[提要] 本文结合常规配电网规划问题的特点，提出在配电网规划优化过程中采用全寿命周期成本（life cycle cost，LCC）分析的思路来选择配电网规划方案。在满足电网安全稳定运行的前提下，给出配电网规划方案全寿命周期成本的计算模型，提出以全寿命周期成本（LCC）最小为目标函数，利用聚类排挤小生境遗传算法对配网路径规划进行优化，通过对不同的开关布置方式进行LCC费用对比分析得到LCC最小的规划方案。最后通过算例证明该方法的可行性和有效性。

关键词：全寿命周期成本；配电网规划；聚类排挤小生境遗传算法；辐射网

中图分类号：F42 文献标识码：A

原标题：基于全寿命周期成本和改进遗传算法的配电网规划研究

收录日期：2016年1月26日

一、引言

配电网网络规划是指在满足对用户供电和网络运行约束的前提下，寻求一组最优的决策变量（变电站位置和容量、馈线的路径和尺寸等），使投资、运行、检修、网损和可靠性损失费用之和最小，使规划方案在满足运行要求的同时经济性最优。在竞争机制不断引入电力市场的今天，配电网规划方法的研究格外受到重视。长期以来，各国学者对这一问题做了大量的研究，文献提出了基于最小费用的配网馈线路径优化，文献将人工智能的算法引入到了配电网规划中，这些方法都能够取得比较好的规划结果，但是它们的目标函数不能很好地反映规划方案的经济性，特别是规划方案全寿命周期经济性。

本文在以上方法的基础上提出了基于全寿命周期成本（Life Cycle Cost，LCC）最小的配电网规划优化方法。与传统方法相比，该方法综合考虑了电网建设项目各个阶段的成本，协调了电网的可靠性和经济性。传统的配电网规划以最少的系统投资来满足某负荷水平的预定可靠度，而系统投资主要考虑电网项目的前期投入资本，忽视了项目实施后的运行、维修、翻新以及报废等诸多后续环节，更缺乏对规划方案全寿命周期内社会成本（如停电损失成本、环保成本）的整体考虑。从长远的观点看，规划方案的运行成本、维护成本、社会成本要远大于它的建设成本，而且先期建设成本的高低对未来运营成本、维护成本和社会成本的高低会产生很大的影响，高的建设成本可能会带来未来运营维护成本的大幅度降低，从而使规划方案在整个寿命周期内的成本降低。因此，有必要从电网建设的全寿命周期角度来进行配电网规划。

二、配电网规划全寿命周期成本

电网建设项目的全寿命周期成本管理是全寿命周期成本管理理论在电力系统的应用。电网建设项目的全寿命周期成本管理以建设项目的全寿命周期内的规划设计、施工建设、运营、维护和报废各个阶段发生的成本为研究对象，以全寿命周期经济效益最优为研究目标，在满足安全、效能和环保的前提下追求工程效益全寿命周期成本最优，寻求最佳配网规划方案，创造最大的经济效益、社会效益和环境效益。配电网的全寿命周期成本指系统从设计到退役的整个期间所发生的费用总和，主要包括：一次性投资成本、运行成本、维护成本、故障成本、设备废弃成本。下面是各种成本的详细计算模型：

（一）一次性投入成本CI。一次性投入成本指配电网在规划设计、建设期间内所付出的一次性成本。主要包括设计阶段的设计成本、建设阶段的设备采购成本、施工安装成本。设备投资费用为Cei，其中第i种设备采购成本和施工安装成本为Ci，M为配电网各种设备的集合，ni为第i种设备的数量；设计阶段的成本为Cds，则一次性投入成本表示如式（1）所示：

CI=Cei+Cds=■niCi+Cds （1）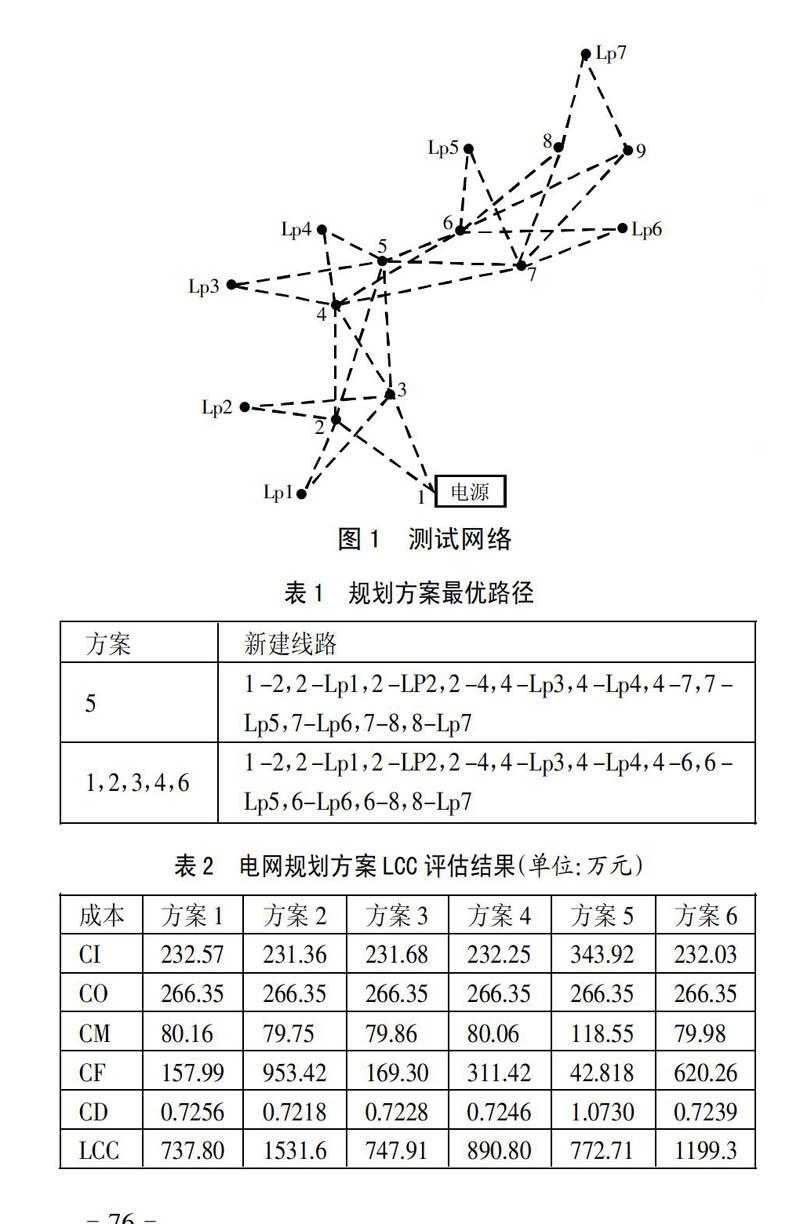

（二）运行成本Co。运行成本就是指配电网在运行期间所需要的一切费用的总和。包括设备损耗费、运行人员培训费等。配电网设备损耗主要包括线路损耗和变压器损耗，而线路损耗主要包括线路导线中的电能损耗、电容器和电缆的绝缘介质损耗以及电晕损耗等；变压器损耗包括与运行电压有关的空载损耗和与电流平方成正比的负载损耗，本文只考虑线路的电能损耗。

1、电能损耗Cec。电能损耗根据最大负荷损耗小时数法进行计算。在已知配电网负荷分布的条件下，根据潮流计算可以得到电网的功率损耗△Pmax，通过最大负荷利用小时数Tmax和功率因数，根据有关手册查得最大负荷损耗时间？子max。可按下式计算全年电能损失△Ws：

△Ws=△Pmax×？子max （2）

乘以电价即可得到配电线路的电能损耗费，即：

Cec=△Ws×Cp （3）

式中，Cec为配电网的线路电能损耗费，Cp为电价。

2、运行人员培训费等成本Cos。

（三）维护成本CM。维护成本指检修人员费用、设备故障检修等费用，贯穿整个设备寿命周期内。许多电力设备的维修周期、维修费用等相对稳定，这样就可以确定维修成本的数学模型。

CM=■？姿i×RCi （4）

式中：？姿i为第i类设备年平均维修次数；RCi为第i类设备平均每次综合维修费用，包括设备检修费和检修人员费用。

（四）故障成本CF。故障成本主要是由于故障停电对电网以及用户造成的经济损失。主要包括停电损失、社会影响损失等。

1、停电损失Coc。在电力市场条件下，停电损失是指电力供应不完全可靠或预期不完全可靠时所造成的全部经济损失。用于衡量可靠性效益高低的停电成本计算比较困难，这是因为停电成本与多种因素有关，其中包括停电发生的时间、停电量、停电持续时间、停电频率及用户类型等。停电损失采用文献中提出的产电比方法进行停电损失的计算，根据某一时期（年）、某一地区内国内生产总值与消耗电能量之比，即产电比Roven，通过Roven计算停电时间内相应的停电损失。研究期间内停电损失可按下式计算：

Coc=■Roven×EENSi （5）

式中：m为配电网的负荷点数；Roven为产电比，单位为元/kWh；EENSi为研究期间内负荷节点的电量不足期望值（Expected Energy Not Supplied）（kWh/期间），可通过系统可靠性计算得到。

2、社会影响损失Cs。社会影响损失主要包括：环境污染防治费用、社会协调费用等。

（五）废弃成本CD。废弃成本指设备在退役过程中进行各种善后处理所需费用。除了支付必要的善后处理（例如废品处理等）费用外，还可以回收一些设备残值。假定用于处置第i种设备所需支付的费用Cied，第i种设备残值为Cier，则废弃成本如式（6）所示：

CD=■（Cied-Cier） （6）

三、基于全寿命周期成本的配电网规划

（一）配电网规划数学模型。应用全寿命周期成本理念进行配电网规划，以配电网规划方案全寿命周期现值成本最小为目标函数，以规划方案可靠性、系统潮流等为约束条件，建立配电网规划的优化模型如下式所示：

minLCC=CI+（CO+CM+CF）×PVsum+CD×PV+U1L辐射网U2非辐射网 （7）

约束条件：

（1）AP=D；

（2）Pi

（3）辐射状网络运行方式。

其中：A为节点关联矩阵；P为网络潮流；D为负荷需求；Pi为支路潮流；Pimax为支路最大允许容量；LCC为设备全寿命周期成本；PVsum=■，按年度投资成本的现值和，N为工程项目寿命周期，r为折现率；PV=■，折现系数；U1是过负荷惩罚系数；L是网络的过负荷（即超过线路的最大允许负荷）的部分，其数值可以通过网络的负荷潮流计算求得；U2是非辐射网惩罚值，其应该设置的很大以优先淘汰不可行的解。其中潮流约束可以通过基于前推回代法的潮流计算来实现；容量约束和辐射状约束都通过构造罚函数的方法来实现。

（二）配电网规划中聚类排挤小生境遗传算法。配电网规划优化是一个多目标、多阶段、离散的、非线性、受约束的混合整数规划问题，常规的数学方法难以处理这样复杂的问题。排挤模型是一种维持群体多样性的选择方法。排挤小生境及其改进遗传算法已被广泛的应用在电力系统优化问题中。其基本思想是：首先比较群体中每两个个体之间的海明距离（或欧氏距离等），若这个距离小于预先指定的距离L，再比较两者的适应度，并对其中适应度较小的个体施加一个较强的罚函数，极大地降低其适应度。这样，对于在距离L之内的两个个体，其中适应度较小的个体经处理后其适应度变得更差，在后面的进化过程中被淘汰的概率就更大。也就是说，在距离L之内将只存在一个优良的个体，从而既维护了群体的多样性，又使得各个个体之间保持一定的距离，且个体能够在整个约束空间中分散开来，从而就实现了一种小生境遗传算法。现有小生境技术能够在一定程度上保持种群的多样性，在搜索空间的不同区域中并行地进化搜索，克服遗传漂移的均匀收敛趋势，具有一定的全局寻优能力。但是这些小生境技术的优化效果和计算速度受小生境数目影响较大，在配电网规划时往往导致寻优结果具有较大波动性。其根本原因是现有算法不能建立并维持稳定的小生境。

聚类的目的是把大量数据点的集合分成若干类，使得每个类中的数据之间最大限度的相似，而不同类中的数据之间最大限度的不同。所有的聚类方法都有自己的聚类判据，常用的聚类判据包括最小化类内距离平方和和最大化类间距离平方和等。类内距离平方和判据适用于聚类中个体间比较接近的场合，而类间距离平方和判据则适用于聚类与聚类间区别比较明显的场合。在确定聚类中心时，本文采用了类间距离平方和最大的判据；在确定所有个体归类时，采用了类内距离平方和最小的判据。将聚类分析与排挤机制结合起来，可以有效地搜索全局极值点，同时可以通过调节最小的聚类半径，控制收敛到的小生境数目，避免找到无效的极值点。

1、编码方案。配电网络可以表示成线路的组合，通过改变线路的状态来改变网络的拓扑结构。将线路用0或1表示，0表示该线路没被选中，1表示该线路被选中，每条线路占据染色体的一个基因，染色体的长度等于规划线路的总数。

2、种群的初始化。考虑配电网的辐射状约束，如果采用随机方法初始化种群会得到大量的不可行解，这将会影响寻优的速度。本文采用图论的知识，随机产生备选网络的生成树，作为遗传算法的初始解，使得初始解均为辐射状的可行解。

3、辐射网判断子程序。经过基因交叉和变异后，染色体所代表的规划方案不一定为辐射网，因此需要进行辐射网判定，本文采用分层广度优先搜索算法进行辐射网判断。以变电站为根节点，搜索与之相连的所有子节点作为下次搜索的根节点，再搜索这些根节点的子节点，以此类推，直到遍历所有节点。如果算法执行中发现某个节点的入线数大于1，则判断为非辐射网，应赋予相应的适应值一个相当大的惩罚值。

4、算法的基本步骤

（1）随机生成初始个体组成初始种群，并设置聚类距离。

（2）将种群中所有个体按适应度值进行降序排序，将适应度最高的个体设为聚类中心，根据类内距离将部分个体归类到该中心。

（3）在剩余个体中重复步骤（2），直到分类结束。

（4）在各个小生境内进行适应值共享小生境遗传算法。

（5）判断终止条件，不满足将返回第（2）步，若满足终止条件，输出结果，算法结束。

四、算例

本文以IEEE RBTS bus-2的一段馈线为例，见图1。图1中虚线表示可能新建的线路，总共28条。Lp1～Lp7为负荷节点，其他节点为分支节点。算法参数设置为：种群大小设为200，最大迭代次数50。电价cp=0.6元/kWh，贴现率为r=6%，产电比为9.65元/kWh，变压器参考价格16.08万元，隔离开关参考价格0.223万元，熔断器参考价格0.045万元，主馈线参考价格20万元/公里，分支线参考价格12万元/公里，规划方案寿命周期20年。（图1）

应用本文提出的算法用Visual studio2005编制了优化程序。对6种不同接线方式进行了计算，6种不同的接线方式为：（1）主干线路有隔离开关，有分支线保护，有备用电源，无备用变压器；（2）主干线路无隔离开关，无分支线保护，无备用电源，无备用变压器；（3）主干线路无隔离开关，有分支线保护，无备用电源，无备用变压器；（4）主干线路有隔离开关，无分支线保护，有备用电源，无备用变压器；（5）主干线路有隔离开关，有分支线保护，有备用电源，有备用变压器；（6）主干线路有隔离开关，无分支线保护，无备用电源，无备用变压器。配电网规划方案最优路径结果见表1。6种不同的接线方式对应的规划方案的LCC计算结果见表2。（表1、表2）

从表1可以看出，根据全寿命周期成本来选择LCC最小的路径规划方案，不同的路径方案，配电网络安装的设备和可靠性不相同，则投入成本、运行维护和故障等成本不同，方案的全寿命周期的总成本也不同，不同的接线方式对应的最优路径不同。例如，方案5的最优路径不同于其他的方案。

规划方案优化时，若只考虑电网项目的前期投入资本，可能选择前期投入资本少的供电方案，但是从长远的角度看，规划方案的运行成本、维护成本、故障成本远大于它的建设成本，所以应综合考虑配电网规划中的全寿命周期成本。对于方案5，在该方案的LCC计算中，因方案的系统可靠性非常高，通过增加备用变压器来提高系统可靠性，故障成本的减小小于设备的投入成本和运行成本的增加，LCC总成本并不是最优，因此虽然方案5的供电可靠性最高，但不是经济性和可靠性最优的规划方案。从表2可以看出，方案1是基于电网全寿命周期成本最小的最优规划方案，此方案的规划路径和开关设备的配置实现了配电网的安全性和经济性的折中，是最优规划方案。

五、结论

本文将全寿命周期成本理论应用于配电网规划优化中，根据配电网的运行特点，建立了配电网规划方案全寿命周期成本详细的计算模型。以全寿命周期经济性最优为目标函数建立配电网规划LCC优化模型，利用聚类排挤小生境遗传算法对配电网规划方案进行优化。通过对实际算例的分析，给出了其最优规划方案和配网开关布置方式，结果验证了本文提出的应用全寿命周期成本对电网建设项目进行决策分析的可行性和有效性，为配电网规划、运行和改造以及电力公司的营运效益提供新的分析方法和辅助决策理论依据，进一步完善了全寿命周期成本管理在电网规划工程中的应用。

主要参考文献：

[1]杨期余.配电网络[M].中国电力出版社，1998.

[2]Satish Jonnavithula，Roy Billinton.Minimum Cost Analysis of Feeder Routing in Distribution System Planning[J].IEEE Transactions on Power Delivery，1996.11.4.

[3]张李盈，范明天.配电网综合规划模型与算法的研究[J].中国电机工程学报，2004.24.6.

[4]Ahmed N U.A Design and Implementaion Model for Life Cycle Cost Management System[J].Information and Management，1995.28.

[5]郭永基.电力系统可靠性分析[M].北京：清华大学出版社电，2003.

[6]张敬平，梁志瑞，苏海锋等.基于改进排挤小生境遗传算法配网无功优化研究[J].继电器，2007.35.10.

[7]于歆杰，王赞基.一种新的聚类方法及其在多峰优化中的应用[J].清华大学学报，2001.45.

[8]R.N.Allen，R.Billinton.A Reliability Test System for Educational Purposes-Basic Distribution System Date and Results[J].IEEE Trans on PowerSystems，1991.6.2.